6.使用个人用户登录域控的成员服务器,如何防止个人用户账号的用户策略生效?
(1)需求:
(2)实战配置步骤
第一步:创建新的策略-并编辑策略
第二步:将策略应用到服务器处在OU
第三步:测试
(1)需求:
比如域控,或者加入域的成员服务器,有时候,我们是直接使用个人域账号登录,但是我们的个人域账号做了很多用户配置策略。我们想使用个人用户登录这些服务器器时候,个人账号的用户策略不生效,如何做呢?方法:做计算机的回环策略即可。
(2)实战配置步骤
策略:计算机策略
对象:计算机对象
配置路径:计算机配置-策略-管理模板-系统-组策略-配置用户策略环回处理模式(已启用:替换)
第一步:创建新的策略-并编辑策略
计算机配置-策略-管理模板-系统-组策略-配置用户策略环回处理模式(已启用:替换)
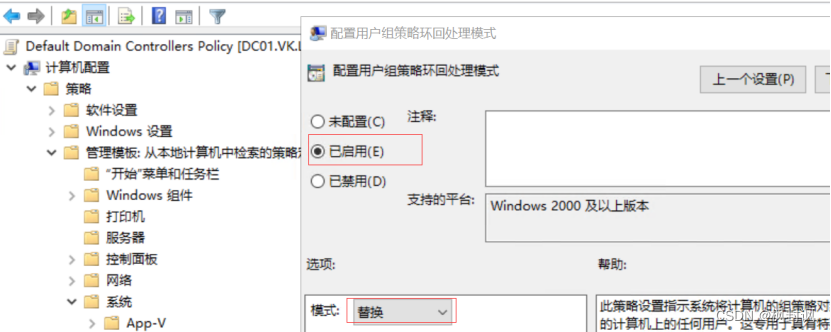
第二步:将策略应用到服务器处在OU
记住,要将策略应用到服务器所在的OU。
第三步:测试
mstsc远程登录加入域的成员服务器。(可以做用户的挂载共享盘的策略进行测试。)
测试命令:
gpresult /h 1.html
start 1.html
查看用户策略生效的情况!!!
相关文章:

6.使用个人用户登录域控的成员服务器,如何防止个人用户账号的用户策略生效?
(1)需求: (2)实战配置步骤 第一步:创建新的策略-并编辑策略 第二步:将策略应用到服务器处在OU 第三步:测试 (1)需求: 比如域控,或者加入域的…...

模拟算法
例题一 算法思路: 纯模拟。从前往后遍历整个字符串,找到问号之后,就⽤ a ~ z 的每⼀个字符去尝试替换即 可。 例题二 解法(模拟 分情况讨论): 算法思路: 模拟 分情况讨论。 计算相邻两个…...
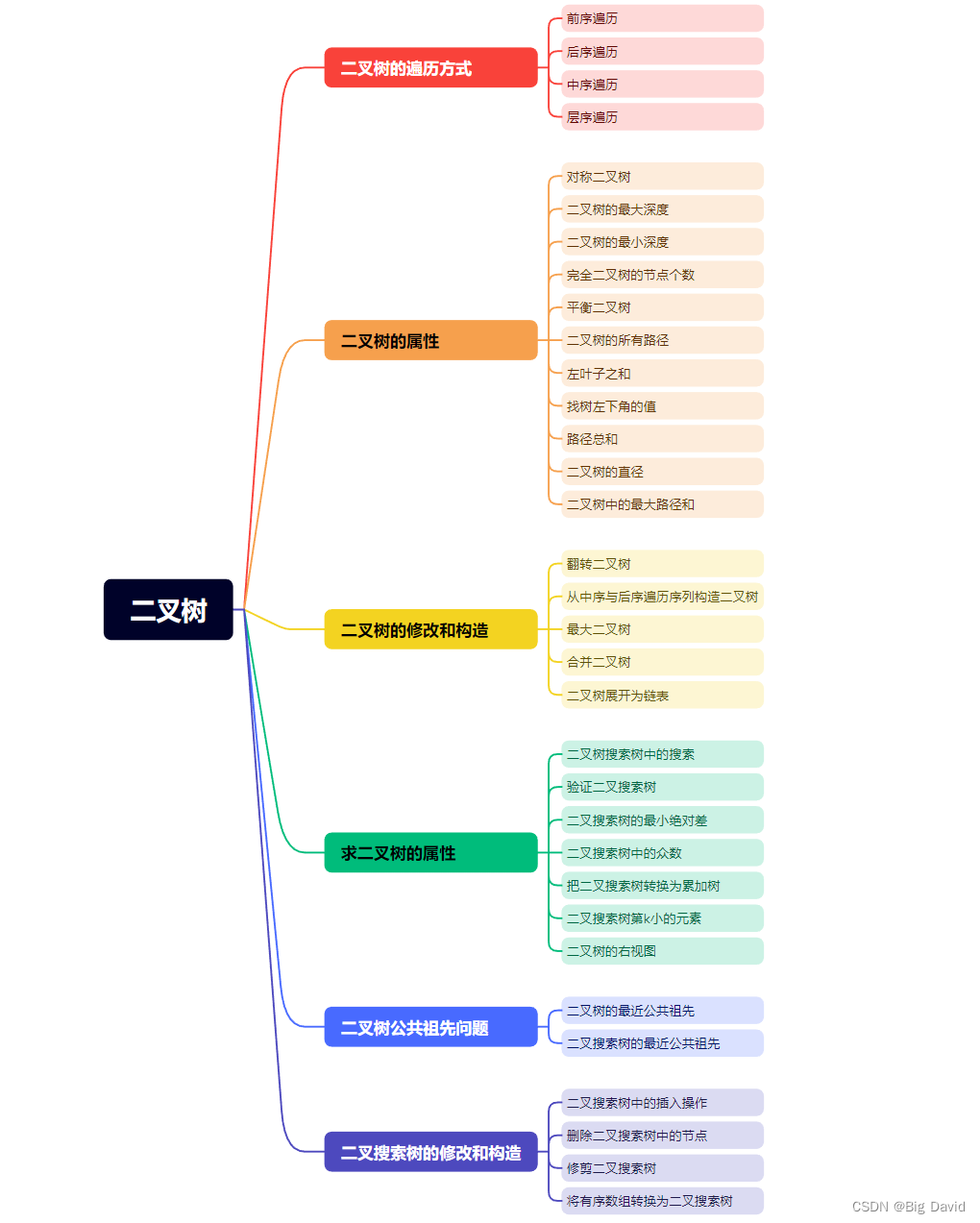
【数据结构刷题专题】—— 二叉树
二叉树 二叉树刷题框架 二叉树的定义: struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(NULL), right(NULL); };1 二叉树的遍历方式 【1】前序遍历 class Solution { public:void traversal(TreeNode* node, vector&…...

基于AWS云服务构建智能家居系统的最佳实践
在当今智能家居时代,构建一个安全、高性能、可扩展和灵活的智能家居系统已经成为许多公司的目标。亚马逊网络服务(AWS)提供了一系列云服务,可以帮助企业轻松构建和管理智能家居系统。本文将探讨如何利用AWS云服务构建一个智能家居系统,并分享相关的最佳实践。 系统架构概述 该…...

Java零基础-集合:Set接口
哈喽,各位小伙伴们,你们好呀,我是喵手。 今天我要给大家分享一些自己日常学习到的一些知识点,并以文字的形式跟大家一起交流,互相学习,一个人虽可以走的更快,但一群人可以走的更远。 我是一名后…...

数据结构与算法-排序算法
1.顺序查找 def linear_search(iters, val):for i, v in enumerate(iters):if v val:return ireturn 2.二分查找 # 升序的二分查找 def binary_search(iters, val):left 0right len(iters)-1while left < right:mid (left right) // 2if iters[mid] val:return mid…...
SpringBoot 文件上传(三)
之前讲解了如何接收文件以及如何保存到服务端的本地磁盘中: SpringBoot 文件上传(一)-CSDN博客 SpringBoot 文件上传(二)-CSDN博客 这节讲解如何利用阿里云提供的OSS(Object Storage Service)对象存储服务保存文件。…...

web渗透测试漏洞流程:红队目标信息收集之资产搜索引擎收集
web渗透测试漏洞流程 渗透测试信息收集---域名信息收集1.域名信息的科普1.1 域名的概念1.2 后缀分类1.3 多重域名的关系1.4 域名收集的作用1.5 DNS解析原理1.6 域名解析记录2. 域名信息的收集的方法2.1 基础方法-搜索引擎语法2.1.1 Google搜索引擎2.1.1.1 Google语法的基本使用…...

UI自动化_id 元素定位
## 导包selenium from selenium import webdriver import time1、创建浏览器驱动对象 driver webdriver.Chrome() 2、打开测试网站 driver.get("你公司的平台地址") 3、使浏览器窗口最大化 driver.maximize_window() 4、在用户名输入框中输入admin driver.find_ele…...

华为OD技术面算法题整理
LeetCode原题 简单 题目编号频次409. 最长回文串 - 力扣(LeetCode)3...

vmware虚拟机下ubuntu扩大磁盘容量
1、扩容: 可以直接在ubuntu setting界面里直接扩容,也可通过vmware命令,如下: vmware提供一个命令行工具,vmware-vdiskmanager.exe,位于vmware的安装目录下,比如 C:/Program Files/VMware/VMwar…...
秋招打卡算法题第一天
一年多没有刷过算法题了,已经不打算找计算机类工作了,但是思来想去,还是继续找吧。 1. 字符串最后一个单词的长度 public static void main(String[] args) {Scanner in new Scanner(System.in);while(in.hasNextInt()){String itemin.nextL…...

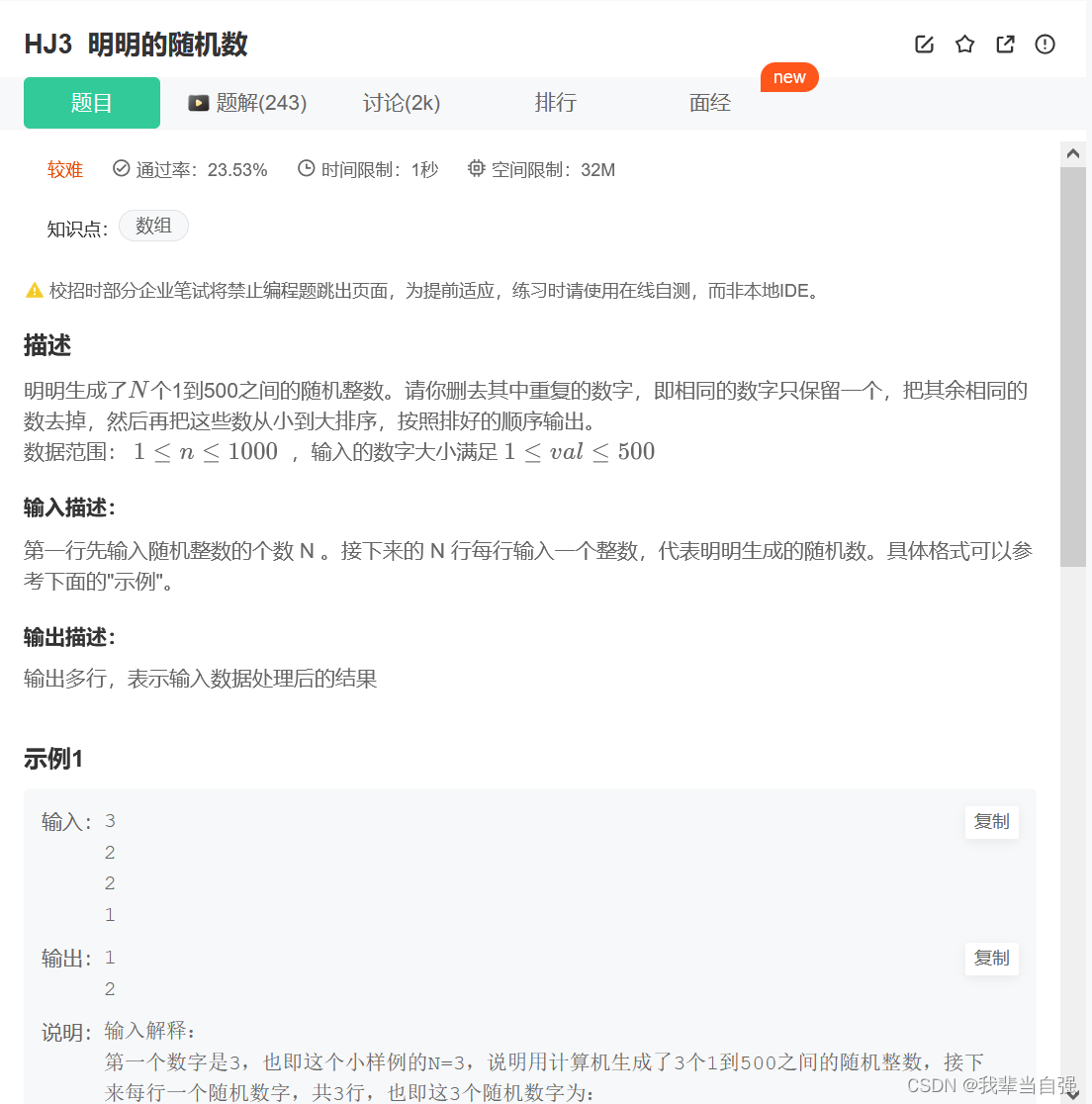
BC98 序列中删除指定数字
题目 描述 有一个整数序列(可能有重复的整数),现删除指定的某一个整数,输出删除指定数字之后的序列,序列中未被删除数字的前后位置没有发生改变。 数据范围:序列长度和序列中的值都满足 1≤�≤…...
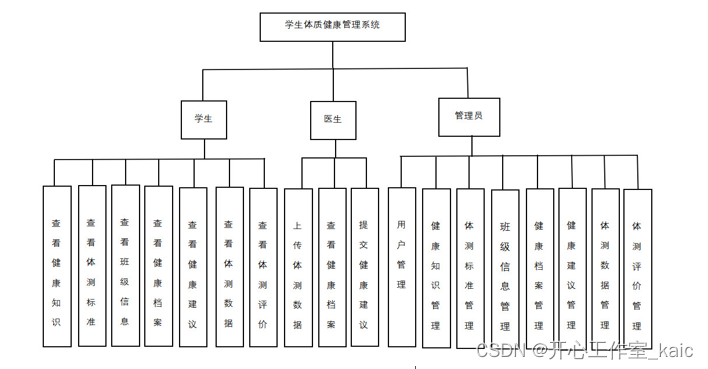
基于Java的学生体质健康管理系统的设计与实现(论文+源码)_kaic
摘 要 随着时代的进步,信息化也在逐渐深入融进我们生活的方方面面。其中也给健康管理带来了新的发展方向。通过对学生体质健康管理的研究与分析发现当下的管理系统还不够全面,系统的性能达不到使用者的要求。因此,本文结合Java的优势和流行性…...

【Linux系统】冯诺依曼与操作系统
什么是冯诺依曼体系结构? 如图即为冯诺依曼大致的体系结构图, 我们知道这些都是由我们的计算机硬件组成 输入设备:键盘, 鼠标, 摄像头, 话筒, 磁盘, 网卡... 输出设备:…...
——form表单的新增特性/h5的新特性)
前端理论总结(html5)——form表单的新增特性/h5的新特性
form表单的新增特性 range:范围 color:取色器 url:对url进行验证 tel:对手机号格式验证 email:对邮箱格式验证 novalidate :提交表单时不验证 form 或 input 域 numbe…...

基于TensorFlow的花卉识别(算能杯)%%%
Anaconda Prompt 激活 TensorFlow CPU版本 conda activate tensorflow_cpu //配合PyCharm环境 直接使用TensorFlow1.数据分析 此次设计的主题为花卉识别,数据为TensorFlow的官方数据集flower_photos,包括5种花卉(雏菊、蒲公英、玫瑰、向日葵…...

Android实现一周时间早中晚排班表
我们要做一个可以动态添加,修改一周早中晚时间排班表,需求图如下: one two 过程具体在这里不描述了,具体查看,https://github.com/yangxiansheng123/WorkingSchedule 上传数据格式: {"friday_plan":"…...
【Java八股面试系列】中间件-Redis
目录 Redis 什么是Redis Redis解决了什么问题 Redis的实现原理 数据结构 String 常用命令 应用场景 List(列表) 常用命令 应用场景 Hash(哈希) 常用命令 应用场景 set(集合) 常见命令编辑 应用场景 Sorted Set(有序集合) 常见命令编辑 应用场景 数据持…...

目前国内体验最佳的AI问答助手:kimi.ai
文章目录 简介图片理解长文档解析 简介 kimi.ai是国内初创AI公司月之暗面推出的一款AI助手,终于不再是四字成语拼凑出来的了。这是一个非常存粹的文本分析和对话工具,没有那些东拼西凑花里胡哨的AIGC功能,实测表明,这种聚焦是对的…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
