【C++练级之路】【Lv.16】红黑树(冰与火的碰撞,红与黑的史诗)

文章目录
- 引言
- 一、红黑树的概念
- 二、红黑树的模拟实现
- 2.1 结点
- 2.2 成员变量
- 2.3 插入
- 情况一:uncle在左,parent在右
- ==如果uncle存在且为红色==:
- ==如果uncle不存在,或者存在且为黑色==:
- 情况二:parent在左,uncle在右
- ==如果uncle存在且为红色==:
- ==如果uncle不存在,或者存在且为黑色==:
- 三、红黑树的验证
- 四、红黑树的性能
- 4.1 优势
- 4.2 适用场景
引言
之前学习的AVL树,是一种平衡二叉搜索树,它追求绝对平衡,从而导致插入和删除性能较差。而今天学习的红黑树,是另一种平衡二叉搜索树,它追求相对平衡,使得增删查改的性能都极佳,时间复杂度皆为O(log2N),是数据结构中的精华,天才般的设想!
一、红黑树的概念
红黑树,顾名思义,其节点有红和黑两种颜色。
之所以新增结点颜色的标记,是因为通过结点着色方式的限制,能够让红黑树的最长路径不超过最短路径的两倍,以保证相对平衡。

红黑树满足五条性质:
- 所有结点非黑即红
- 根结点为黑色
- NIL结点为黑色
- 红色结点的子结点必为黑色
- 任意结点到其叶子NIL结点的所有路径,都包含相同的黑色结点
在红黑树中,NIL节点(也称为空节点)是叶子节点的一种特殊表示。它们不是实际存储数据的节点,而是树结构中的占位符,用于定义树的边界。所有的红黑树都以NIL节点为叶子节点,这些NIL节点在视觉上通常不被画出来。
性质解读:
- 性质4:表明不能有连续的红色结点
- 性质4+性质5:
- 理论最短路径:全为黑色结点
- 理论最长路径:红黑相间

这样,就保证了最长路径不超过最短路径的两倍。
二、红黑树的模拟实现
2.1 结点
enum Color
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Color _col;RBTreeNode(const pair<K, V>& kv): _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};
细节:
- 使用三叉链,增加了指向parent的指针
- 使用KV模型,数据存储键值对pair
- 结点储存颜色,同时颜色使用枚举
- 结点的颜色初始化为红色
说明:为什么结点的颜色初始化为红色呢?因为插入新节点时(不为根部),如果插入黑色,就会直接破坏性质5,导致每条路径黑结点数目不同;而如果插入红色,有可能不会破坏性质4,所以结点初始化为红色更优。
2.2 成员变量
template<class K, class V>
class RBTree
{
protected:typedef RBTreeNode<K, V> Node;
public:
protected:Node* _root = nullptr;
};
2.3 插入
因为红黑树也是二叉搜索树,所以默认成员函数和遍历与之前写的没什么不同,这里重点讲解红黑树的插入。
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandparent = parent->_parent;if (grandparent->_right == parent)//uncle在左,parent在右{Node* uncle = grandparent->_left;if (uncle && uncle->_col == RED)//uncle为红,变色+向上调整{parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;parent = cur->_parent;}else//uncle为空或为黑,变色+旋转{if (parent->_right == cur)//左单旋{RotateL(grandparent);parent->_col = BLACK;grandparent->_col = RED;}else//右左旋{RotateR(parent);RotateL(grandparent);cur->_col = BLACK;grandparent->_col = RED;}}}else//parent在左,uncle在右{Node* uncle = grandparent->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;parent = cur->_parent;}else{if (parent->_left == cur)//右单旋{RotateR(grandparent);parent->_col = BLACK;grandparent->_col = RED;}else//左右旋{RotateL(parent);RotateR(grandparent);cur->_col = BLACK;grandparent->_col = RED;}}}}_root->_col = BLACK;return true;
}
思路:
- 以二叉搜索树的方式正常插入
- 讨论并调整结点的颜色,以及调整结构,使之满足红黑树的性质
循环条件:while (parent && parent->_col == RED)
保证了parent存在且为红,grandparent存在且为黑
情况一:uncle在左,parent在右
如果uncle存在且为红色:

处理方法:
- 将parent和uncle变黑,grandparent变红
- cur = grandparent,parent = cur->_parent,继续向上调整
- 防止grandparent为根节点却变红,在循环结束后将根节点变为黑色
如果uncle不存在,或者存在且为黑色:
当cur在右部外侧时:
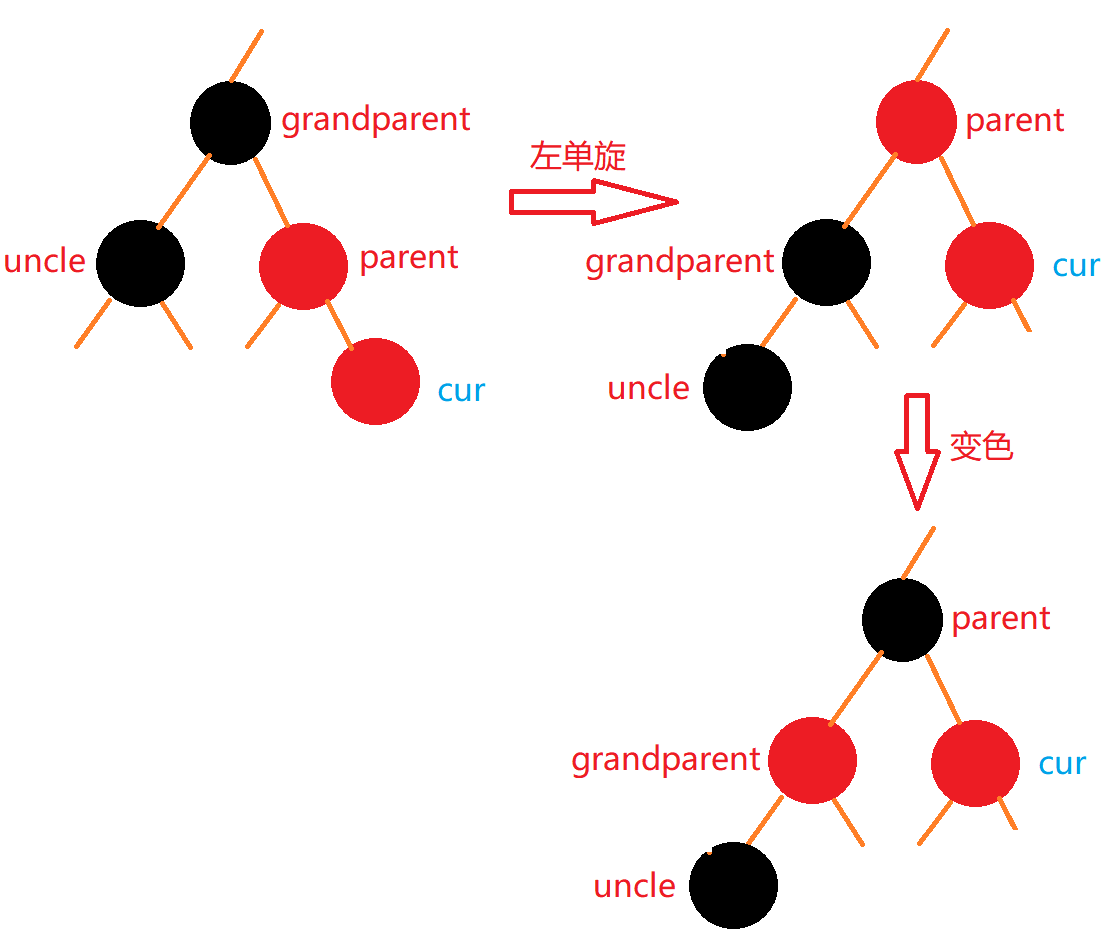
处理方法:
- 先对grandparent进行左单旋
- 再将parent变黑,grandparent变红
当cur在右部内侧时:
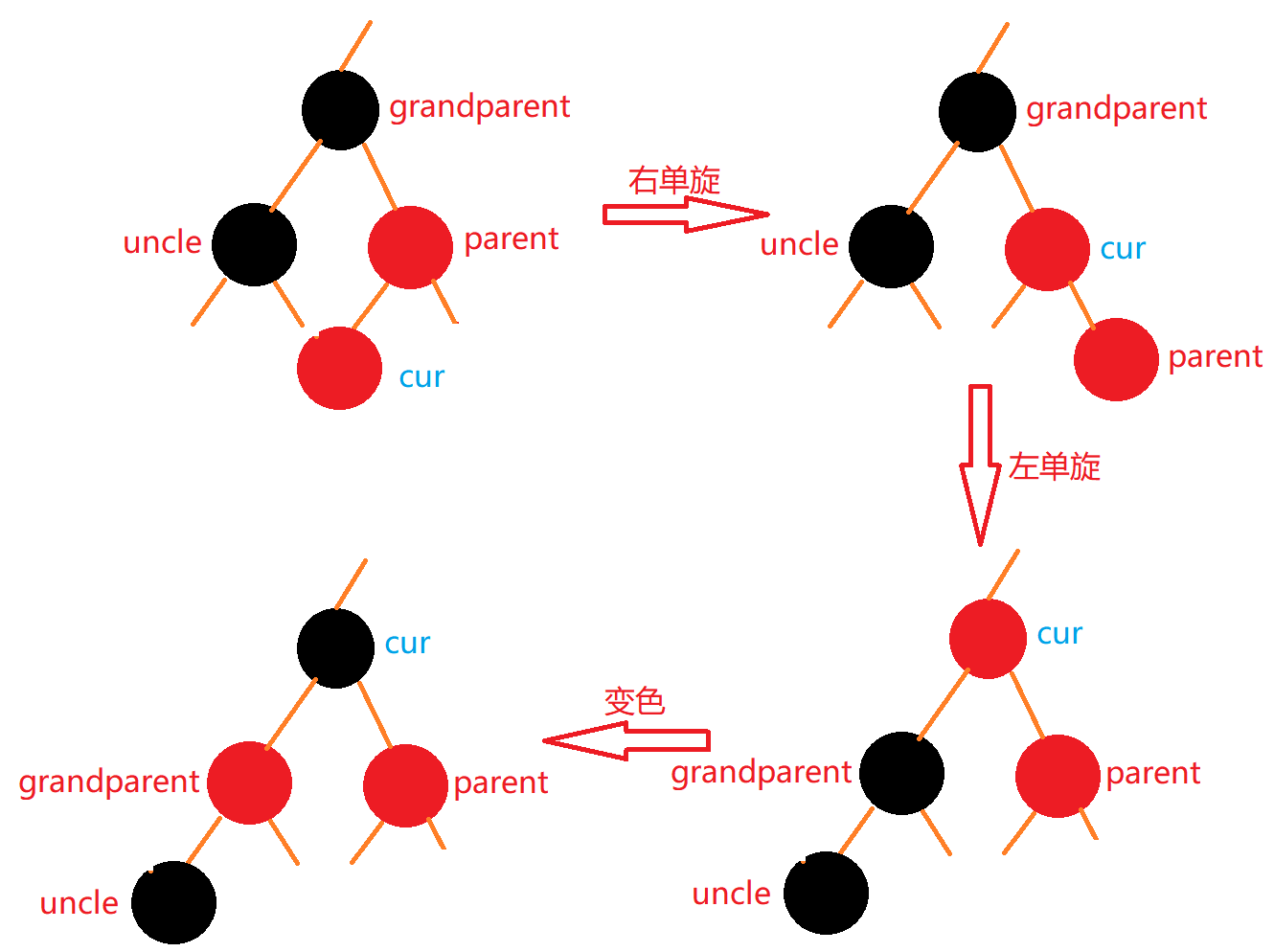
处理方法:
- 先对parent进行右单旋
- 再对grandparent进行左单旋
- 最后将cur变黑,grandparent变红
情况二:parent在左,uncle在右
如果uncle存在且为红色:

处理方法:
- 将parent和uncle变黑,grandparent变红
- cur = grandparent,parent = cur->_parent,继续向上调整
- 防止grandparent为根节点却变红,在循环结束后将根节点变为黑色
如果uncle不存在,或者存在且为黑色:
当cur在左部外侧时:

处理方法:
- 先对grandparent进行右单旋
- 再将parent变黑,grandparent变红
当cur在左部内侧时:
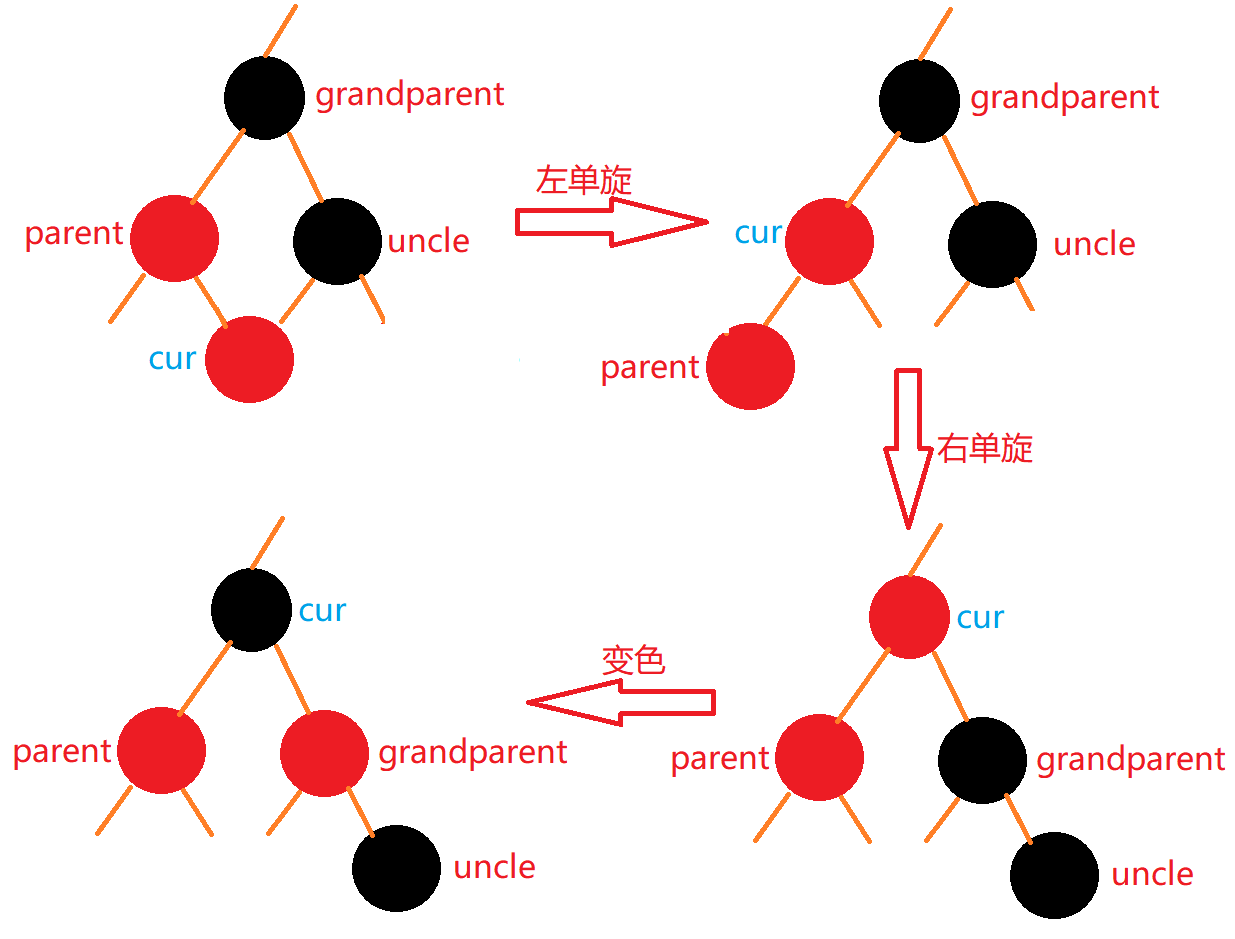
处理方法:
- 先对parent进行左单旋
- 再对grandparent进行右单旋
- 最后将cur变黑,grandparent变红
红黑树插入的核心口诀:uncle存在且为红,变色+向上调整,uncle不存在或为黑,变色+旋转
附上旋转的实现:
void RotateL(Node* parent)
{Node* grandparent = parent->_parent;Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL){subRL->_parent = parent;}subR->_left = parent;parent->_parent = subR;if (grandparent){if (grandparent->_right == parent){grandparent->_right = subR;}else{grandparent->_left = subR;}}else{_root = subR;}subR->_parent = grandparent;
}void RotateR(Node* parent)
{Node* grandparent = parent->_parent;Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}subL->_right = parent;parent->_parent = subL;if (grandparent){if (grandparent->_right == parent){grandparent->_right = subL;}else{grandparent->_left = subL;}}else{_root = subL;}subL->_parent = grandparent;
}
三、红黑树的验证
bool IsBalance()
{if (_root && _root->_col == RED){cout << "根结点为红色" << endl;return false;}int benchMark = 0;//基准值Node* cur = _root;while (cur){if (cur->_col == BLACK){++benchMark;}cur = cur->_right;}return Check(_root, 0, benchMark);
}bool Check(Node* root, int blackNum, int benchMark)
{if (root == nullptr){if (blackNum != benchMark){cout << "某条路径黑色结点数量不相等" << endl;return false;}return true;}if (root->_col == BLACK){++blackNum;}if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << "存在连续的红色结点" << endl;return false;}return Check(root->_left, blackNum, benchMark)&& Check(root->_right, blackNum, benchMark);
}
细节:
- 验证根节点是否为黑
- 先计算出一条路径的黑色结点个数作为基准值,再在递归中比较每条路径的黑色结点是否相等
- 若该节点为红,检测其parent是否为红,判断是否存在连续的红色节点
四、红黑树的性能
4.1 优势
红黑树是高效的平衡二叉树,增删改查的时间复杂度都是O( l o g 2 N log_2 N log2N),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对AVL树而言,降低了插入和旋转的次数。
4.2 适用场景
因此,在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。

相关文章:

【C++练级之路】【Lv.16】红黑树(冰与火的碰撞,红与黑的史诗)
快乐的流畅:个人主页 个人专栏:《C语言》《数据结构世界》《进击的C》 远方有一堆篝火,在为久候之人燃烧! 文章目录 引言一、红黑树的概念二、红黑树的模拟实现2.1 结点2.2 成员变量2.3 插入情况一:uncle在左ÿ…...

政安晨:【Keras机器学习实践要点】(三)—— 编写组件与训练数据
政安晨的个人主页:政安晨 欢迎 👍点赞✍评论⭐收藏 收录专栏: TensorFlow与Keras实战演绎机器学习 希望政安晨的博客能够对您有所裨益,如有不足之处,欢迎在评论区提出指正! 介绍 通过 Keras,您可以编写自定…...
数据库系统概论(超详解!!!) 第四节 关系数据库标准语言SQL(Ⅲ)
1.连接查询 连接查询:同时涉及多个表的查询 连接条件或连接谓词:用来连接两个表的条件 一般格式: [<表名1>.]<列名1> <比较运算符> [<表名2>.]<列名2> [<表名1>.]<列名1> BETWEEN [&l…...

如何使用Python进行网络安全与密码学【第149篇—密码学】
👽发现宝藏 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【点击进入巨牛的人工智能学习网站】。 用Python进行网络安全与密码学:技术实践指南 随着互联网的普及,网络…...
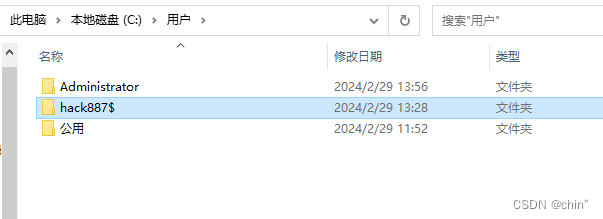
应急响应-Web2
应急响应-Web2 1.攻击者的IP地址(两个)? 192.168.126.135 192.168.126.129 通过phpstudy查看日志,发现192.168.126.135这个IP一直在404访问 , 并且在日志的最后几条一直在访问system.php ,从这可以推断 …...

复试专业前沿问题问答合集8-1——CNN、Transformer、TensorFlow、GPT
复试专业前沿问题问答合集8-1——CNN、Transformer、TensorFlow、GPT 深度学习中的CNN、Transformer、TensorFlow、GPT大语言模型的原理关系问答: Transformer与ChatGPT的关系 Transformer 是一种基于自注意力机制的深度学习模型,最初在论文《Attention is All You Need》…...

用Python做一个植物大战僵尸
植物大战僵尸是一个相对复杂的游戏,涉及到图形界面、动画、游戏逻辑等多个方面。用Python实现一个完整的植物大战僵尸游戏是一个大工程,但我们可以简化一些内容,做一个基础版本。 以下是一个简化版的植物大战僵尸游戏的Python实现思路&#…...
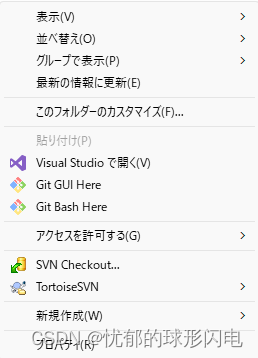
Win11文件右键菜单栏完整显示教程
近日公司电脑升级了win11,发现了一个小麻烦事,如下图: 当我想使用svn或git的时候必须要多点一下,这忍不了,无形之中加大了工作量! 于是,菜单全显示教程如下: 第一步:管…...

【Python实用标准库】argparser使用教程
argparser使用教程 1.介绍2.基本使用3.add_argument() 参数设置4.参考 1.介绍 (一)argparse 模块是 Python 内置的用于命令项选项与参数解析的模块,其用主要在两个方面: 一方面在python文件中可以将算法参数集中放到一起&#x…...

伦敦金与纸黄金有什么区别?怎么选?
伦敦金与纸黄金都是与黄金相关的投资品种,近期黄金市场的上涨吸引了投资者的关注,那投资者想开户入场成为黄金投资者应该选择纸黄金还是伦敦金呢?两者有何区别呢?下面我们就来讨论一下。 伦敦金是一种起源于伦敦的标准化黄金交易合…...
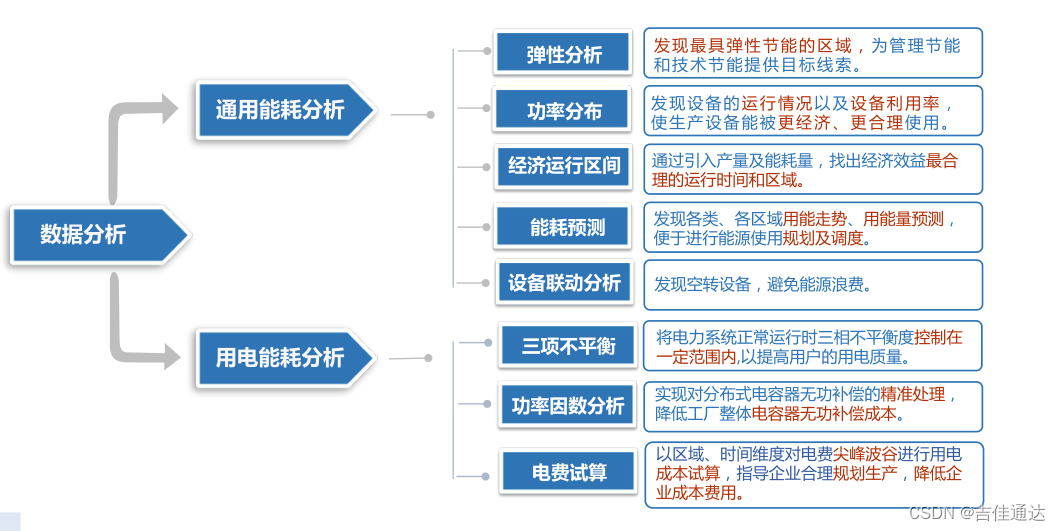
化工企业能源在线监测管理系统,智能节能助力生产
化工企业能源消耗量极大,其节能的空间也相对较大,所以需要控制能耗强度,保持更高的能源利用率。 化工企业能源消耗现状 1、能源管理方面 计量能源消耗时,计量器具存在问题,未能对能耗情况实施完全计量,有…...

C/C++ 一些使用网站收集...
C/C 标准 各种语言协议标准文档 open-std.org 网站 C语言标准文档 open-std.org C基金会网站 C/C 标准库网站 c/c 标准库 cplusplus.com 网站 c/c标准库 cppreference.com 网站 C Core Guidelines【isocpp.org】 C/C 发展 C现有状态及未来规划【isocpp.org】...

2024可以搜索夸克网盘的方法
截止2024可以搜索夸克网盘的方法 6miu盘搜 6miu盘搜是一个强大的网盘搜索工具,它汇集了多个网盘平台的资源,包括百度网盘、163网盘、金山快盘等,可以帮助用户快速找到所需的资料。6miu盘搜的一个显著特点是它的资源更新速度快,可以搜索到最新的资源。此外,6miu盘搜的界面清爽…...
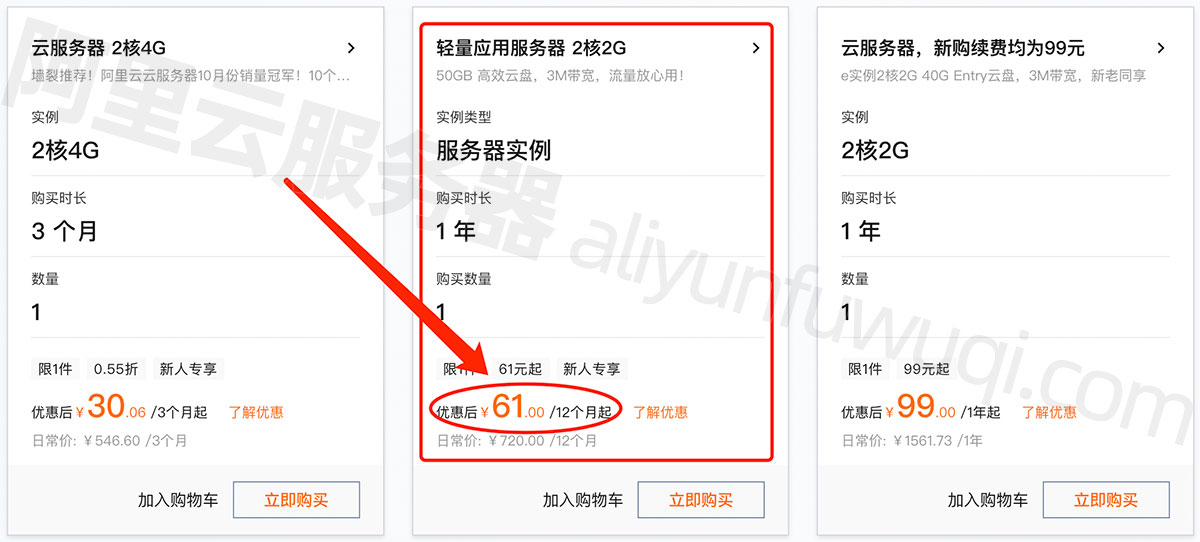
2024年最新阿里云服务器价格表_CPU内存+磁盘+带宽价格
2024年阿里云服务器租用费用,云服务器ECS经济型e实例2核2G、3M固定带宽99元一年,轻量应用服务器2核2G3M带宽轻量服务器一年61元,ECS u1服务器2核4G5M固定带宽199元一年,2核4G4M带宽轻量服务器一年165元12个月,2核4G服务…...
)
300.【华为OD机试】跳房子I(时间字符串排序—JavaPythonC++JS实现)
本文收录于专栏:算法之翼 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目二.解题思路三.题解代码Python题解代码JAVA题解代码C/C++题解代码JS题解代码四.代码讲解(Ja…...
的命令)
linux ln Linux 系统中用于创建链接(link)的命令
linux 命令基础汇总 命令&基础描述地址linux curl命令行直接发送 http 请求Linux curl 类似 postman 直接发送 get/post 请求linux ln创建链接(link)的命令创建链接(link)的命令linux linklinux 软链接介绍linux 软链接介绍l…...

mysql按照查询条件进行排序和统计一个字段中每个不同数值出现的次数
1.比如学生表 如何显示查询结果的顺序根据放置的顺序查询 <select id"selectNames" resultType"Student">select * from student_table where 11<if test"studentList! null">and name in<foreach item"item" ind…...
深度学习基础知识
本文内容来自https://zhuanlan.zhihu.com/p/106763782 此文章是用于学习上述链接,方便自己理解的笔记 1.深度学习的网络结构 深度学习是神经网络的一种特殊形式,典型的神经网络如下图所示。 神经元:表示输入、中间数值、输出数值点。例如&…...
UE4_旋转节点总结一
一、Roll、Pitch、Yaw Roll 围绕X轴旋转 飞机的翻滚角 Pitch 围绕Y轴旋转 飞机的俯仰角 Yaw 围绕Z轴旋转 飞机的航向角 二、Get Forward Vector理解 测试: 运行: 三、Get Actor Rotation理解 运行效果: 拆分旋转体测试一&a…...

Dockerfile将jar部署成docker容器
将jar包copy到linux,新建Dockerfile文件 -rw-r--r-- 1 root root 52209844 Mar 25 22:55 data-sharing-0.0.1-SNAPSHOT.jar -rwxrwxrwx 1 root root 227 Mar 25 22:57 Dockerfile [rootlocalhost mnt]# pwd /mntDockerfile内容 # 指定基础镜像 FROM java:8-a…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
