C++_回文串
目录
回文子串
最长回文子串
分割回文串 IV
分割回文串 II
最长回文子序列
让字符串成为回文串的最少插入次数
回文子串
647. 回文子串

思路,i j表示改范围内是否为回文串,
②倒着遍历是为了取出dp[i + 1][j - 1]
③i j 只有一对,不会重复,其实就是遍历
参考代码
class Solution {
public:int countSubstrings(string s) {int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n));int ret = 0;for(int i = n - 1; i >= 0; i--){// dp[i][i] = true;// for(int j = i + 1; j < n; j++)// {// if(s[i] == s[j])// dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;// if(dp[i][j]) ret++;//判断每一次// }for(int j = i; j < n; j++){if(s[i] == s[j])dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;//只有最后一层会越界,但是if(dp[i][j])ret++;}}// return ret + n;return ret;}
};最长回文子串
5. 最长回文子串
思路区间[i, j] 是true时候再判断
参考代码
class Solution {
public:string longestPalindrome(string s) {int n = s.size();vector<vector<int>> dp(n, vector<int>(n));int maxlen = 1, begin = 0;for(int i = n - 1; i >= 0; i--){dp[i][i] = true;for(int j = i + 1; j < n; j++){if(s[i] == s[j])dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;if(dp[i][j] && j - i + 1 > maxlen)maxlen = j - i + 1, begin = i;}}return s.substr(begin, maxlen);}
};分割回文串 IV
1745. 分割回文串 IV
用区间[i, j]即可分成三段 ,只要i j 不同,三段必不相同
参考代码
class Solution {
public:bool checkPartitioning(string s) {int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n));for(int i = n - 1; i >= 0; i--)for(int j = i; j < n; j++)if(s[i] == s[j])dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;for(int i = 1; i <= n - 2; i++)for(int j = i; j <= n - 2; j++)if(dp[0][i - 1] && dp[i][j] && dp[j + 1][n - 1])return true;return false;}
};分割回文串 II
132. 分割回文串 II

刚开始打算用dp[i, j]区间内需要的次数 ,发现逻辑就不对,以左右单个字符拎出来,在min剩下的,最小分割的位置很可能在中间某个位置;所以打算重新遍历数组,和139. 单词拆分的思路很像,[0, i] 区间存放的就是最小分割次数
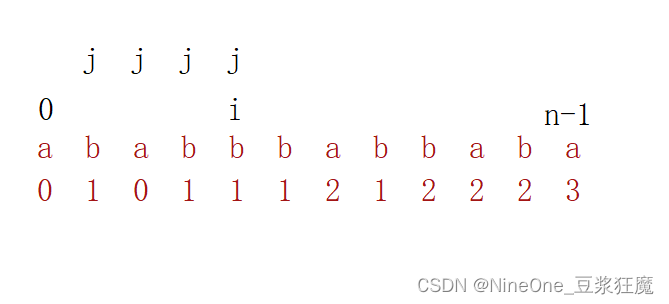
参考代码
class Solution {
public:int minCut(string s) {// int n = s.size();// vector<vector<int>> dp(n, vector<int>(n));// for(int i = n - 1; i >= 0; i--)// {// for(int j = i + 1; j < n; j++)// {// if(s[i] == s[j])// dp[i][j] = dp[i + 1][j - 1];// else// dp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1;// }// }// return dp[0][n - 1];int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n));for(int i = n - 1; i >= 0; i--)for(int j = i; j < n; j++)if(s[i] == s[j]) dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] : true;vector<int> times(n, INT_MAX);times[0] = 0;for(int i = 1; i < n; i++){if(dp[0][i]) times[i] = 0;elsefor(int j = 1; j <= i; j++)if(dp[j][i])times[i] = min(times[i], times[j - 1] + 1);}return times[n - 1];}
};最长回文子序列
516. 最长回文子序列
因为[i ,j] 表示的是区间内的最长回文子序列,这里我不怎么能直接理解,这里的j每次往后走,应该是去尝试匹配s[i],那么有人会说s[i] 可能和[i + 1, j - 1] 区间内有匹配了,那么用s[j]去匹配,不就少了一个吗?其实不然,这时候中间不管是否和s[i]相同,【 s[i] ,中间字符,s[j] 】就是一个回文子序列,这样是最大的;如果不相等,因为说了,状态表示的是区间内的最长回文子序列,这时候去已经有的区间里面找最长的已知区间就是[i + 1, j] 和 [i , j + 1],那为什么不去[i, j] 里找,因为没有啊,这时候,dp[i][j]是左值呀
参考代码
class Solution {
public:int longestPalindromeSubseq(string s) {int n = s.size();vector<vector<int>> dp(n, vector<int>(n, 1));for(int i = n - 1; i >= 0; i--){for(int j = i + 1; j < n; j++){if(s[i] == s[j])dp[i][j] = j - i > 1 ? dp[i + 1][j - 1] + 2 : j - i + 1;elsedp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);}}return dp[0][n - 1];}
};让字符串成为回文串的最少插入次数
1312. 让字符串成为回文串的最少插入次数
dp表示的是区间[i, j] 内需要添加的最小次数,同样的道理,如果不相等就是去消除s[i] 或者s[j],消除伴随着 +1,也就是dp[i][j] = min(dp[i][j - 1], dp[i + 1][j]) + 1,你可能会感觉不对, 有可能是min(dp[i][j - 2], dp[i + 2][j])那么随之后面就要+2,但是这个时候可能s[i] 和s[j - 1]是相等的啊,那么就多添加了一个字符
参考代码
class Solution {
public:int minInsertions(string s) {int n = s.size();vector<vector<int>> dp(n, vector<int>(n));for(int i = n - 1; i >= 0; i--){for(int j = i + 1; j < n; j++){if(s[i] == s[j])dp[i][j] = dp[i + 1][j - 1];elsedp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1;}}return dp[0][n - 1];}
};总结:通过区间[i, j]来表示每个区间是否为回文串 ,是的话在进行怎样怎样的操作
我的错误发生: i总是写错i++, 注意力不集中
相关文章:

C++_回文串
目录 回文子串 最长回文子串 分割回文串 IV 分割回文串 II 最长回文子序列 让字符串成为回文串的最少插入次数 回文子串 647. 回文子串 思路,i j表示改范围内是否为回文串, ②倒着遍历是为了取出dp[i 1][j - 1] ③i j 只有一对,不会重复…...
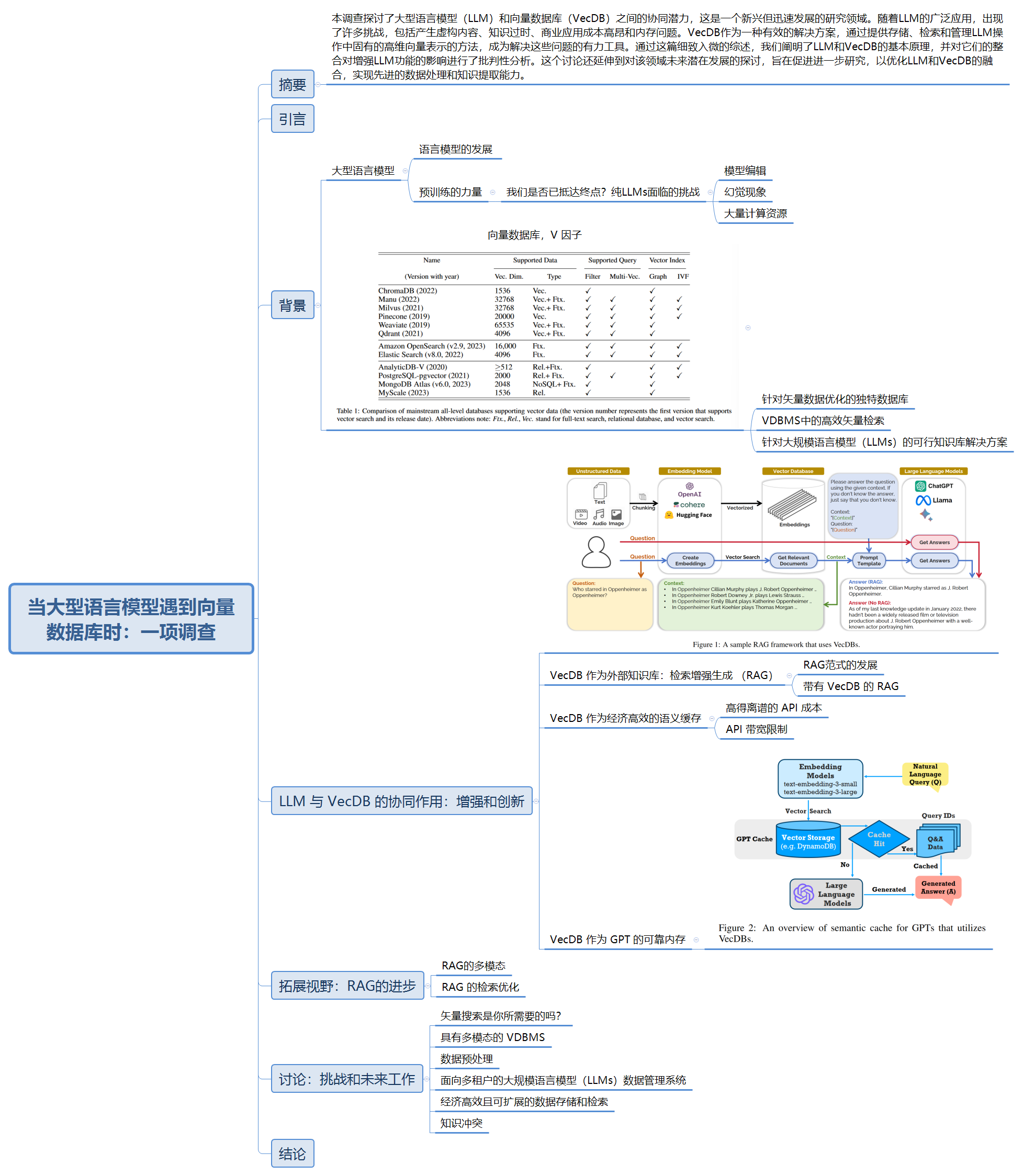
【阅读论文】When Large Language Models Meet Vector Databases: A Survey
摘要 本调查探讨了大型语言模型(LLM)和向量数据库(VecDB)之间的协同潜力,这是一个新兴但迅速发展的研究领域。随着LLM的广泛应用,出现了许多挑战,包括产生虚构内容、知识过时、商业应用成本高昂…...

兼职副业大揭秘:六个潜力满满的赚钱途径
亲爱的朋友,你对兼职副业充满好奇与期待,这非常好!在此,我将为你分享一些能够助你赚取额外收入的兼职副业建议。以下是六个颇具潜力的兼职副业方向,希望能为你的探索之路提供些许启发。 1,网络调查与市场洞…...
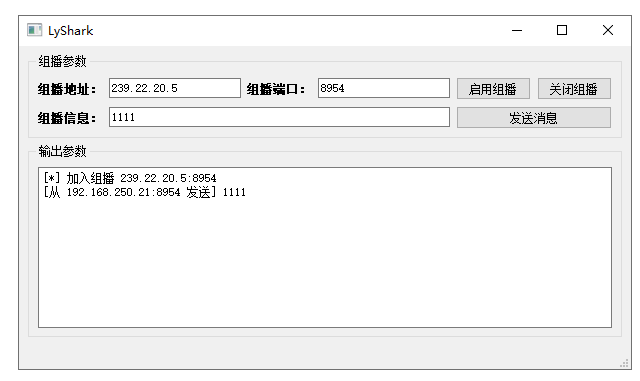
C++ Qt开发:QUdpSocket实现组播通信
Qt 是一个跨平台C图形界面开发库,利用Qt可以快速开发跨平台窗体应用程序,在Qt中我们可以通过拖拽的方式将不同组件放到指定的位置,实现图形化开发极大的方便了开发效率,本章将重点介绍如何运用QUdpSocket组件实现基于UDP的组播通信…...
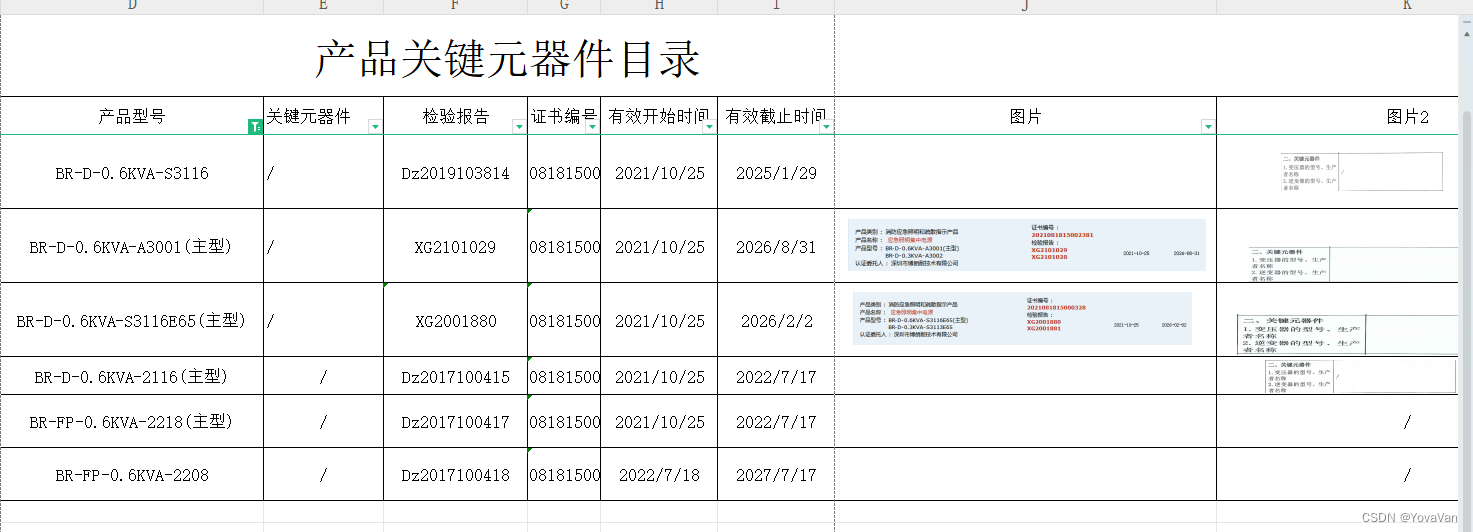
excel 表中有图片并在筛选特定行时,只显示该行的图片
建议:选中excel 表中某张图片,CtrlA,选中所有图片。再右键,在菜单中选设置对象格式 在属性里按下图设置, 生效之后,筛选某个产品的时候,就不会显示其他的不符合筛选条件的产品的图片了。...
【QA】MySQL多表查询详解
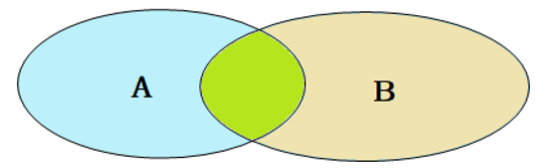
文章目录 前言关系型数据库中数据表之间的关系数据准备数据内容表间关系 基础查询 | 全部查询多表查询分类1 | 连接查询内连接外连接 | 左外连接外连接 | 右外连接自连接 | 自连接自连接 | 联合查询 分类2 | 子查询返回结果分类 | 标量子查询返回结果分类 | 列子查询返回结果分…...

【Entity Framework】 EF三种开发模式
【Entity Framework】 EF三种开发模式 文章目录 【Entity Framework】 EF三种开发模式一、概述二、DataBase First2.1 DataBase First简介2.2 DataBase First应用步骤2.3 DataBase First总结 三、Model First3.1 Model First简介3.2 Model First实现步骤 四、Code First4.1 Cod…...
)
数据分析---SQL(5)
目录 子查询单行子查询多行子查询视图(View)创建视图使用视图更新视图视图的优缺点存储过程存储过程的创建存储过程的参数存储过程的优缺点可能导致性能问题避免存储过程引入性能问题子查询 子查询是指在一个查询语句中嵌套另一个查询语句,内部的查询语句称为子查询,外部的…...
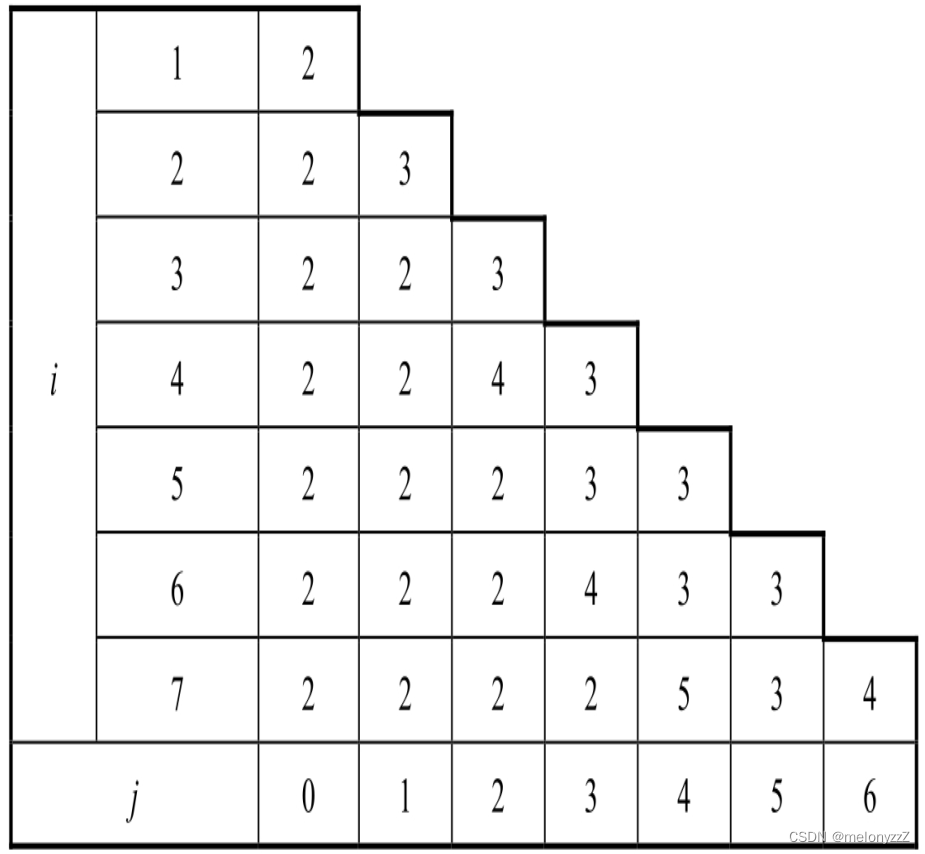
《剑指 Offer》专项突破版 - 面试题 93 : 最长斐波那契数列(C++ 实现)
题目链接:最长斐波那契数列 题目: 输入一个没有重复数字的单调递增的数组,数组中至少有 3 个数字,请问数组中最长的斐波那契数列的长度是多少?例如,如果输入的数组是 [1, 2, 3, 4, 5, 6, 7, 8]࿰…...
代码随想录算法训练营第五十五天|583. 两个字符串的删除操作、72. 编辑距离
583. 两个字符串的删除操作 刷题https://leetcode.cn/problems/delete-operation-for-two-strings/description/文章讲解https://programmercarl.com/0583.%E4%B8%A4%E4%B8%AA%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E5%88%A0%E9%99%A4%E6%93%8D%E4%BD%9C.html视频讲解https://…...

StringRedisTemplate Autowired注入为空解决
如下注入方式报空指针异常: java.lang.NullPointerException: null Autowiredprivate StringRedisTemplate redisTemplate; 解决办法:查看该类上有没有加注解,如Component等,没加的话加上。 还有一种是在工具类中使用,…...
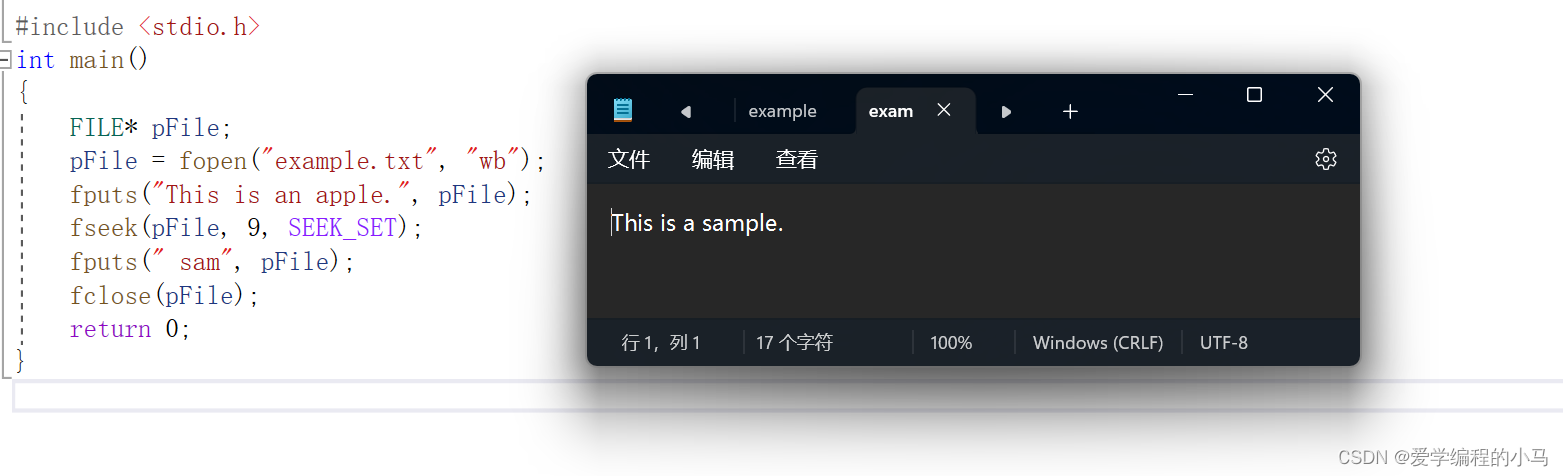
c语言:文件操作
1. 为什么使⽤⽂件? 如果没有⽂件,我们写的程序的数据是存储在电脑的内存中,如果程序退出,内存回收,数据就丢失 了,等再次运⾏程序,是看不到上次程序的数据的,如果要将数据进⾏持久…...
C#事件实例详解
一、什么是事件? 在C#中,事件(event)是一种特殊的类成员,它允许类或对象通知其他类或对象发生了某些事情。 从语法上看,事件的声明类似于字段,但它们在功能和行为上有一些重要的区别。 从技术角度来说,事件实际上是一个封装了事件订阅和取消订阅功能的委托字段。…...
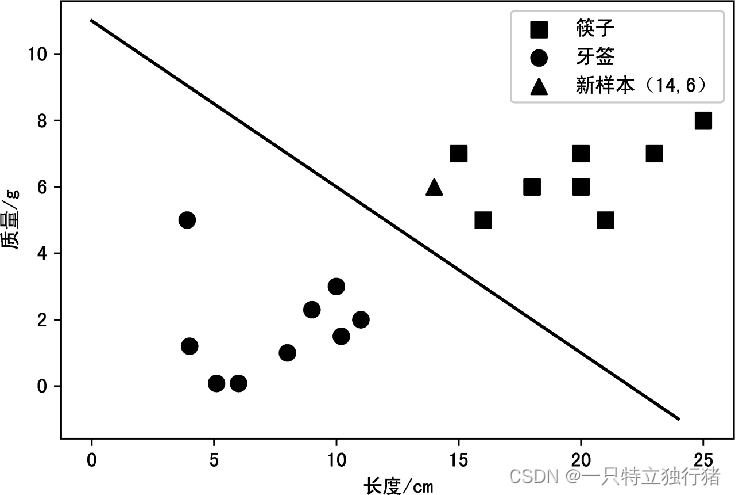
零基础机器学习(3)之机器学习的一般过程
文章目录 一、机器学习一般过程1.数据获取2.特征提取3.数据预处理①去除唯一属性②缺失值处理A. 均值插补法B. 同类均值插补法 ③重复值处理④异常值⑤数据定量化 4.数据标准化①min-max标准化(归一化)②z-score标准化(规范化) 5.…...

用java做一个双色球彩票系统
代码如下: import java.util.Random; public class HelloWorld{public static void main(String[] args){//1、生成中奖号码 int[] arrcreateNumber();for (int i 0;i<arr.length;i) {System.out.print(arr[i]" ");}}public static int[] createNu…...
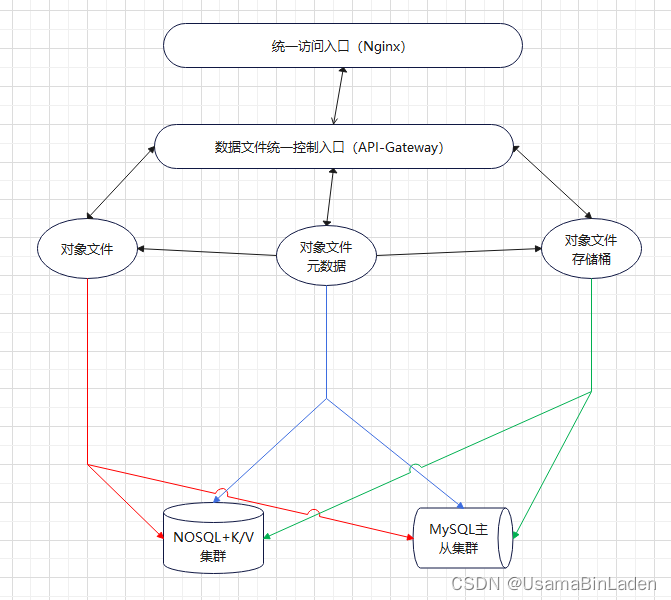
某对象存储元数据集群改造流水账
软件产品:某厂商提供的不便具名的对象存储产品,核心底层技术源自HDFS和Amazon S3,元数据集群采用了基于MongoDB的NOSQL数据库产品和MySQL数据库产品相结合。 该产品的元数据逻辑示意图如下: 业务集群现状:当前第3期建…...
——filter、foearch、for in 、for of 、for的区别以及返回值)
前端理论总结(js)——filter、foearch、for in 、for of 、for的区别以及返回值
Filter: 用途:用于筛选数组中符合条件的元素,返回一个新数组。 返回值:返回一个新数组,包含经过筛选的元素。 Foreach: 用途:遍历数组中的每个元素,执行回调函数。 返回值&#x…...
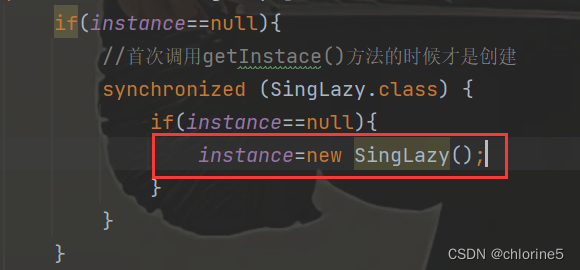
【JavaEE初阶系列】——多线程案例一——单例模式 (“饿汉模式“和“懒汉模式“以及解决线程安全问题)
目录 🚩单例模式 🎈饿汉模式 🎈懒汉模式 ❗线程安全问题 📝加锁 📝执行效率提高 📝指令重排序 🍭总结 单例模式,非常经典的设计模式,也是一个重要的学科&#x…...
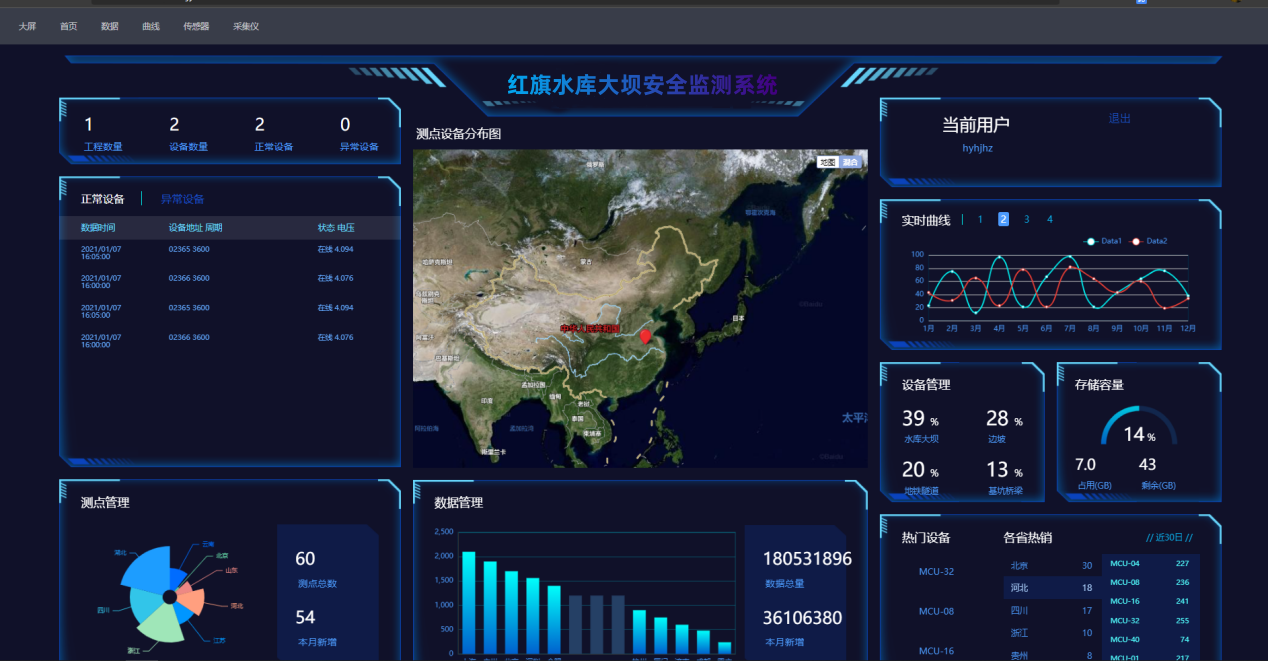
革新水库大坝监测:传统软件与云平台之比较
在水库大坝的监测管理领域,传统监测软件虽然曾发挥了重要作用,但在多方面显示出了其局限性。传统解决方案通常伴随着高昂的运维成本,需要大量的硬件支持和人员维护,且软件整合和升级困难,限制了其灵活性和扩展性。 点击…...
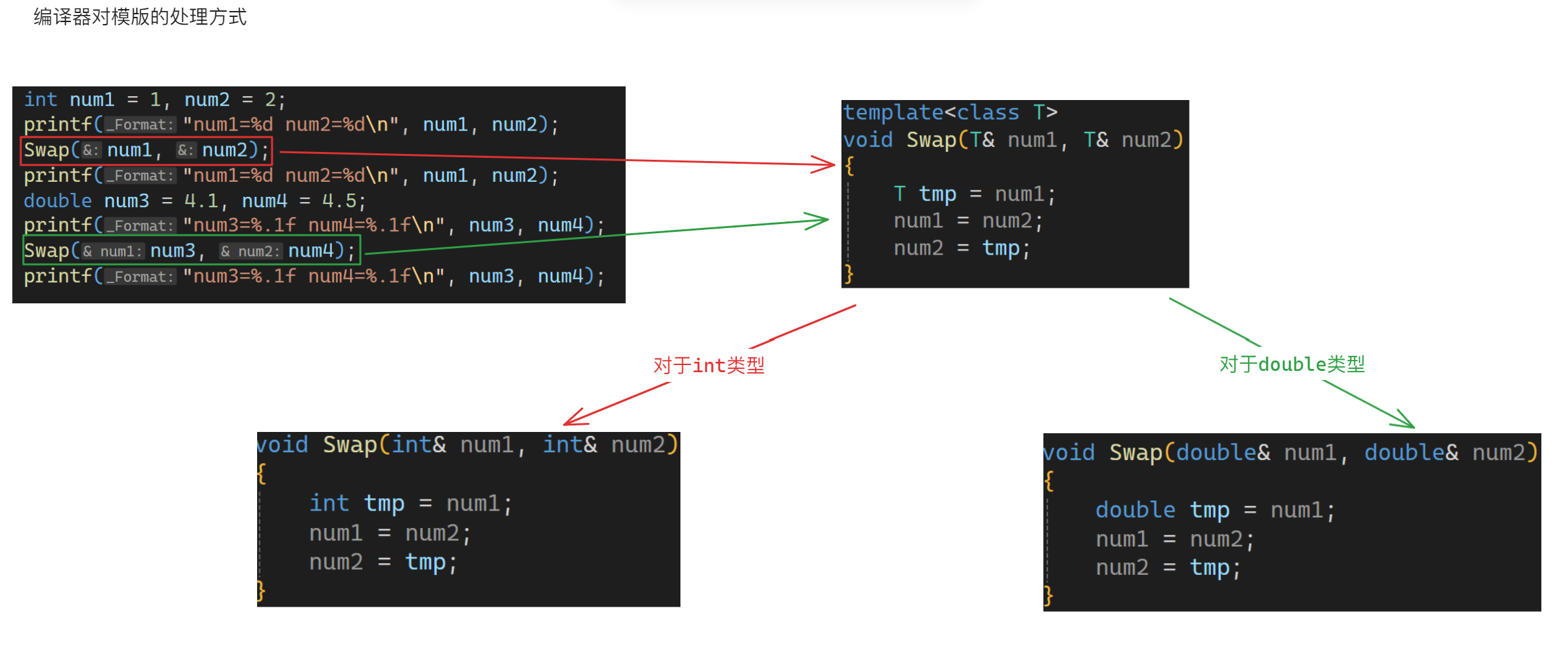
C++模版(基础)
目录 C泛型编程思想 C模版 模版介绍 模版使用 函数模版 函数模版基础语法 函数模版原理 函数模版实例化 模版参数匹配规则 类模版 类模版基础语法 C泛型编程思想 泛型编程:编写与类型无关的通用代码,是代码复用的一种手段。 模板是泛型编程…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...
