[STL]priority_queue类及反向迭代器的模拟实现

🪐🪐🪐欢迎来到程序员餐厅💫💫💫
今日主菜: priority_queue类及反向迭代器
主厨:邪王真眼
主厨的主页:Chef‘s blog
所属专栏:c++大冒险
向着c++,塔塔开!
[本节目标]
-
1.仿函数
-
2.priority_queue
-
3.反向迭代器
一.仿函数
1.1仿函数是什么
仿函数(Functor)是一种重载了函数调用运算符(operator())的类对象,他的使用方法看起来与函数极其相似,却又有不同,因此成为仿函数
1.2仿函数的定义与使用
我们现在写一个可以比较两个变量大小的仿函数以及函数
template<class T>
class Less
{bool operator()(const T&a,const T&b ){return a < b;}
};
template<class T>bool Less(const T& a, const T& b ){return a < b;}那么问题来了,仿函数的优势是什么呢?
我们知道有时候为了在函数中调用别的函数我们需要传一个叫做函数指针的东西,简单的函数还好,复杂的函数的指针是真的难看懂,于是乎,仿函数横空出世,你要用它就传个他的类就行,一下子容易多了。
二、priority_queue
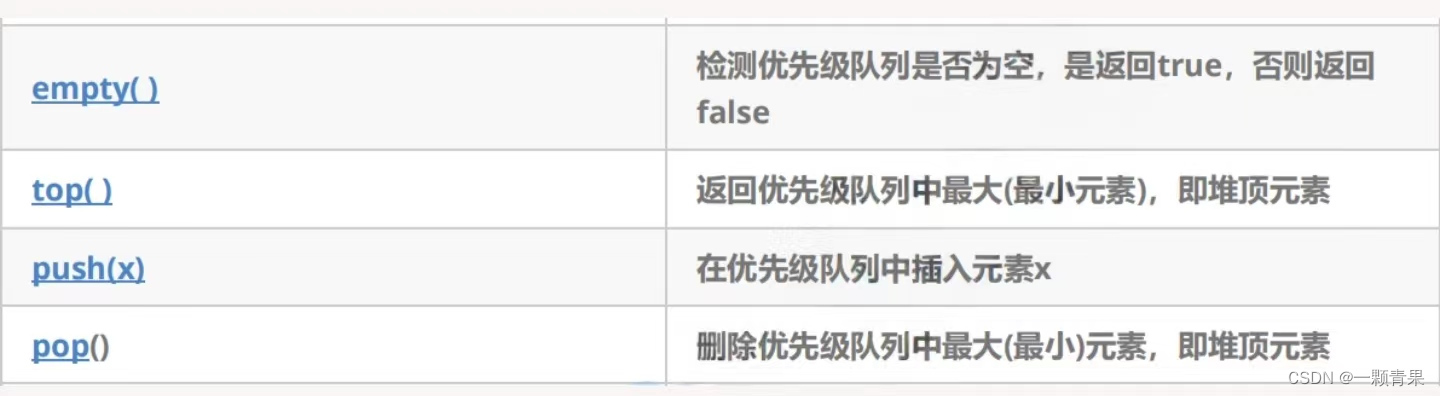
2.1 priority_queue的介绍
- empty():检测容器是否为空
- size():返回容器中有效元素个数
- front():返回容器中第一个元素的引用
- push_back():在容器尾部插入元素
- pop_back():删除容器尾部元素
2.2成员变量
template<class T, class Container = vector<T>, class Compare = Less<T>>class priority_queue{public://函数private:Container _con;};2.3empty
bool empty(){reutrn _con.empty();}2.4size
返回容器适配器的元素个数
size_t size(){return _con.size();}2.5top
返回堆顶元素
注意事项:我们的返回值是const类型,没有非const,这是因为如果你用非const就可能导致堆顶元素修改,进而导致结构不再是大堆或小堆。
constT& top()const{_con.front();}2.6push
入堆
- 1.先尾插
- 2.在向上调整
void push(T& val){_con.push_back(val);UpAdjust();}void UpAdjust(size_t number)//大堆{int child = number - 1;int parent = child = (child-1) / 2;while (child){if (_con[child] > _con[parent]){swap(_con[child], _con[parent]);child = parent;parent = (child-1) / 2;}elsebreak;}}这里我们既要思考,如果建一个小堆那就要在写一个函数,可是他们两个函数只有

这里需要改变,一个是>,一个是<。
于是乎,我们立刻想到了再加一个模板参数,用它来处理这个大于小于的问题,
如下:
template<class T>
class Less
{bool operator()(const T&a,const T&b ){return a < b;}
};
template<class T>
class Greater
{bool operator()(const T& a, const T& b){return a > b;}
}; void push(T& val){_con.push_back(val);UpAdjust();}Compare com;void UpAdjust(size_t number)//大堆{int child = number - 1;int parent = child = (child-1) / 2;while (child){if (com(_con[parent] , _con[child])){swap(_con[child], _con[parent]);child = parent;parent = (child-1) / 2;}elsebreak;}}2.7pop
出堆
这个就比较难了,为了保证堆的结构尽可能不被破坏以降低时间复杂度,我们选择:
- 先把第一个元素和最后一个元素交换位置
- 最后删除最后一个元素。
- 在对堆顶进行向下调整法
- 构造一个仿函数模板对象,再利用重载的()运算符进行比较
template<class T>
class Less
{bool operator()(const T&a,const T&b ){return a < b;}
};
template<class T>
class Greater
{bool operator()(const T& a, const T& b){return a > b;}
}; Compare com;void DownAdjust(size_t size){int parent = 0;int child = parent * 2+1;while (child<size){if (child<size&&com(_con[child], _con[child + 1]))child++;if (com(_con[parent], _con[child])){swap(_con[child], _con[parent]);parent = child;child = parent * 2 + 1;}elsebreak;}}void pop(){swap(_con[0], _con[size() - 1]);
_con.pop_back();DownAdjust(size());}三、反向迭代器
反向迭代器是一种适配器,它是根据不同容器的正向迭代器,来生成对应的反向迭代器。
反向迭代器的rbegin对应迭代器的end位置,rend对应begin位置。
3.1 成员变量
细节:
- 使用struct,标明公有属性
- 成员变量是一个正向迭代器
template <class Iterator,class Ref,class Ptr>
struct ReverseItreator
{typedef ReverseIterator<Iterator, Ref, Ptr> self;Iterator it;
};3.2默认成员函数
写一个缺省的构造,别的编译器自动生即可。
ReverseItreator(Iterator val=Iterator()):it(val){}3.3operator*
Ref operator*(){Iterator its = it;its--;return *its;}3.4operator--
self operator--()
{return ++it;
}
self operator--()const
{Iterator its = it;++it;return its;
}3.5operator++
self operator++(){return --it;}self operator++()const{Iterator its = it;--it;return its;}3.6operator->
Ptr operator->(){return & (*it);}3.7operator==,operator!=
bool operator==(const self&s){return it = s.it;}bool operator !=(const self& s){return it = s.it;}3.8反向迭代器的应用
在容器中,以vector举例
template<class T>
class vector
{
public:typedef T* Iterator;typedef const T* Const_Iterator;typedef ReverseIterator<Iteartor, T&, T*> Reverse_Iterator;typedef ReverseIterator<Iteartor, constT&,cosnt T*> Const_Reverse_Iterator;Iterator end(){return _finish;}Const_Iterator end()const{return _finish;}Iterator begin(){return _start;}Const_Iterator begin()const{return _start;}private:T* _start;T* _finish;
};反向迭代器函数:
Reverse_Iterator rbegin(){return (Reverse_Iterator)end();}Const_Reverse_Iterator rbegin()const{return (Const_Reverse_Iterator)end();}Reverse_Iterator rend(){return (Reverse_Iterator)begin();}Const_Reverse_Iterator rend()const{return (Const_Reverse_Iterator)begin();}这时候我们就要提个问题了,就拿rbegin了,来说吧
看看这个函数怎么样:
Reverse_Iterator begin(){return _finish;}乍一看似乎完全没问题,但是但是,如果是list你咋办呢,是deque你咋办呢,他们都没有这个
_finish成员变量啊,所以我们一开始就说了,它是根据不同容器的正向迭代器,来生成对应的反向迭代器。反向迭代器去调用正向迭代器的实现方法才能保证他的普适性。
总结
- 仿函数的用法及优势,并在priority_queue适配器中加以应用
- 对priority_queue进行了了解和模拟,
- 实现很久前就提到的了反向迭代器,对迭代器这个概念有了更深的了解。
感觉有用的话就点个赞支持一下吧

相关文章:

[STL]priority_queue类及反向迭代器的模拟实现
🪐🪐🪐欢迎来到程序员餐厅💫💫💫 今日主菜: priority_queue类及反向迭代器 主厨:邪王真眼 主厨的主页:Chef‘s blog 所属专栏:c大冒险 向着c&…...

vue2 脚手架
安装 文档:https://cli.vuejs.org/zh/ 第一步:全局安装(仅第一次执行) npm install -g vue/cli 或 yarn global add vue/cli 备注:如果出现下载缓慢:请配置npm 淘宝镜像: npm config set regis…...

【OpenStack】OpenStack实战之开篇
目录 那么,OpenStack是什么?云又是什么?关于容器应用程序OpenStack如何适配其中?如何设置它?如何学会使用它?推荐超级课程: Docker快速入门到精通Kubernetes入门到大师通关课AWS云服务快速入门实战我的整个职业生涯到目前为止一直围绕着为离线或隔离网络设计和开发应用程…...

Python实现WebSocket通信
WebSocket是一种在单个TCP连接上进行全双工通信的协议,位于 OSI 模型的应用层。 与传统的HTTP请求-响应模型不同,WebSocket的最大特点就是,服务器可以主动向客户端推送信息,客户端也可以主动向服务器发送信息,实现实时性和互动性…...
MATLAB 自定义生成直线点云(详细介绍) (47)
MATLAB 自定义生成直线点云 (详细介绍)(47) 一、算法介绍二、具体步骤二、算法实现1.代码2.效果一、算法介绍 通过这里的直线生成方法,可以生成模拟直线的点云数据,并通过调整起点、终点、数量和噪声水平等参数来探索不同类型的直线数据。这种方法可以用于测试、验证和开…...
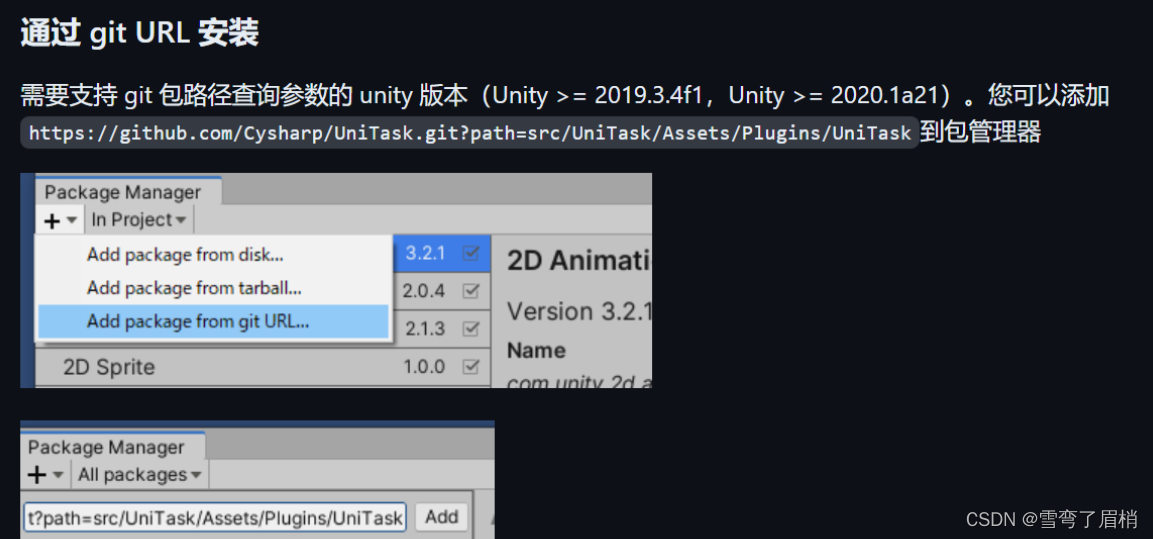
UniTask 异步任务
文章目录 前言一、UniTask是什么?二、使用步骤三、常用的UniTask API和示例1.编写异步方法2.处理异常3.延迟执行4.等待多个UniTask或者一个UniTas完成5.异步加载资源示例6.手动控制UniTask的完成状态7.UniTask.Lazy延迟任务的创建8.后台线程切换Unity主线程9.不要返…...
【git分支管理策略】如何高效的管理好代码版本
目录 1.分支管理策略 2.我用的分支管理策略 3.一些常见问题 1.分支管理策略 分支管理策略就是一些经过实践后总结出来的可靠的分支管理的办法,让分支之间能科学合理、高效的进行协作,帮助我们在整个开发流程中合理的管理好代码版本。 目前有两套Git…...

css的transition详解
CSS的transition属性是一个简写属性,用于设置四个过渡效果属性,以在元素的状态改变时创建平滑的动画效果。这四个属性分别是: transition-property: 定义应用过渡效果的CSS属性名称。当指定的CSS属性改变时,过渡效果将…...

agent利用知识来做规划:《KnowAgent: Knowledge-Augmented Planning for LLM-Based Agents》笔记
文章目录 简介KnowAgent思路准备知识Action Knowledge的定义Planning Path Generation with Action KnowledgePlanning Path Refinement via Knowledgeable Self-LearningKnowAgent的实验结果 总结参考资料 简介 《KnowAgent: Knowledge-Augmented Planning for LLM-Based Age…...

01 React新建开发环境
https://create-react-app.dev/docs/getting-started npx create-react-app my-appJSX使用表达式嵌入 function App() {const count 100;function getSelfName() {return "SelfName"}return (<div>Hello World!<div>{This is Javascript message~!}&l…...
nginx--解决响应头带Set-Cookie导致的验证失败
解决响应头带Set-Cookie导致的验证失败 前言给nginx.conf 设置Secure配置完成后会发现cookie就不会发生变化了 前言 在用nginx做代理的时候,会发现nginx在访问不同ip请求的时候会带setCookie 导致后端就是放开cookie验证,在访问玩这个链接他更新了cooki…...
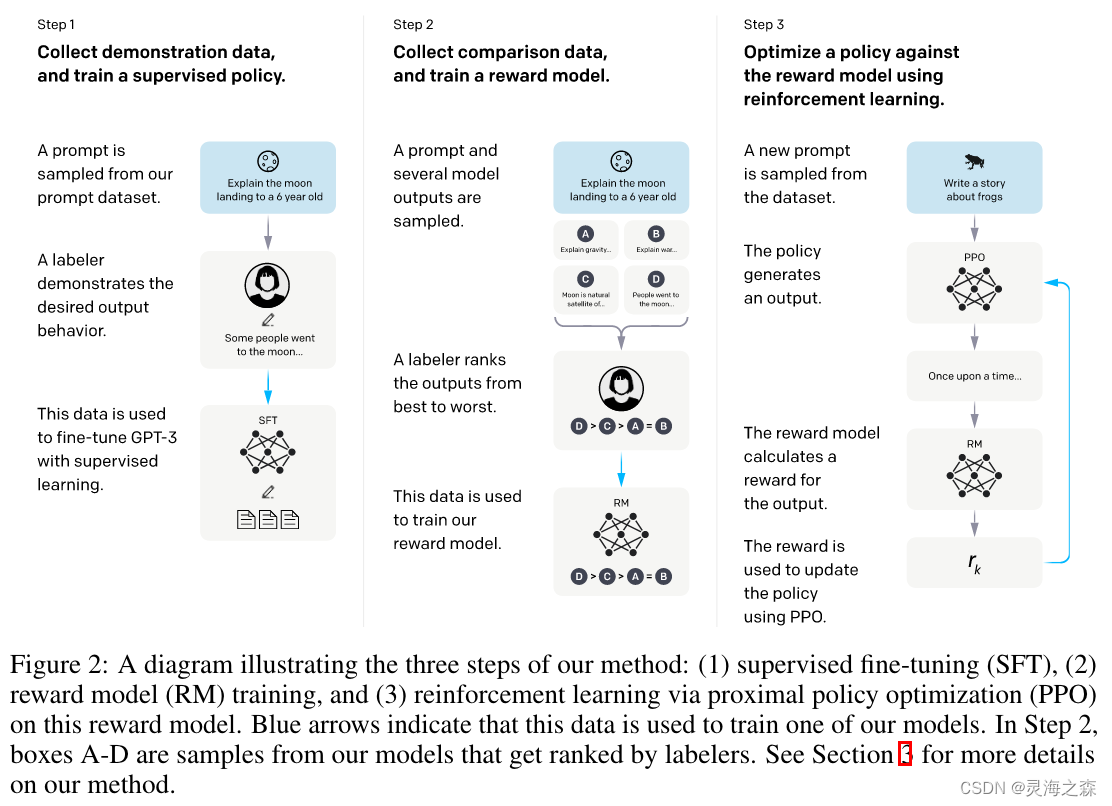
InstructGPT的流程介绍
1. Step1:SFT,Supervised Fine-Tuning,有监督微调。顾名思义,它是在有监督(有标注)数据上微调训练得到的。这里的监督数据其实就是输入Prompt,输出相应的回复,只不过这里的回复是人工…...

docker容器下部署hbase并在springboot中通过jdbc连接
我在windows的docker中部署了一个hbase服务,然后用springboot连接到此服务并访问数据。 详情可参考项目中的README.md。项目中提供了用于构建镜像的dockerfile,以及测试代码。 项目连接: https://gitee.com/forgot940629/hbase_phoenix_sprin…...

Qt——智能指针实战
目录 前言正文一、理论介绍1、QPointer2、QScopedPoint3、QSharedPoint4、QWeakPoint 二、实战演练1、QPoint2、QScopedPoint3、QSharedPointa、示例一b、示例二 4、QWeakPoint END、总结的知识与问题 参考 前言 智能指针的使用,对很多程序员来说,都算是…...
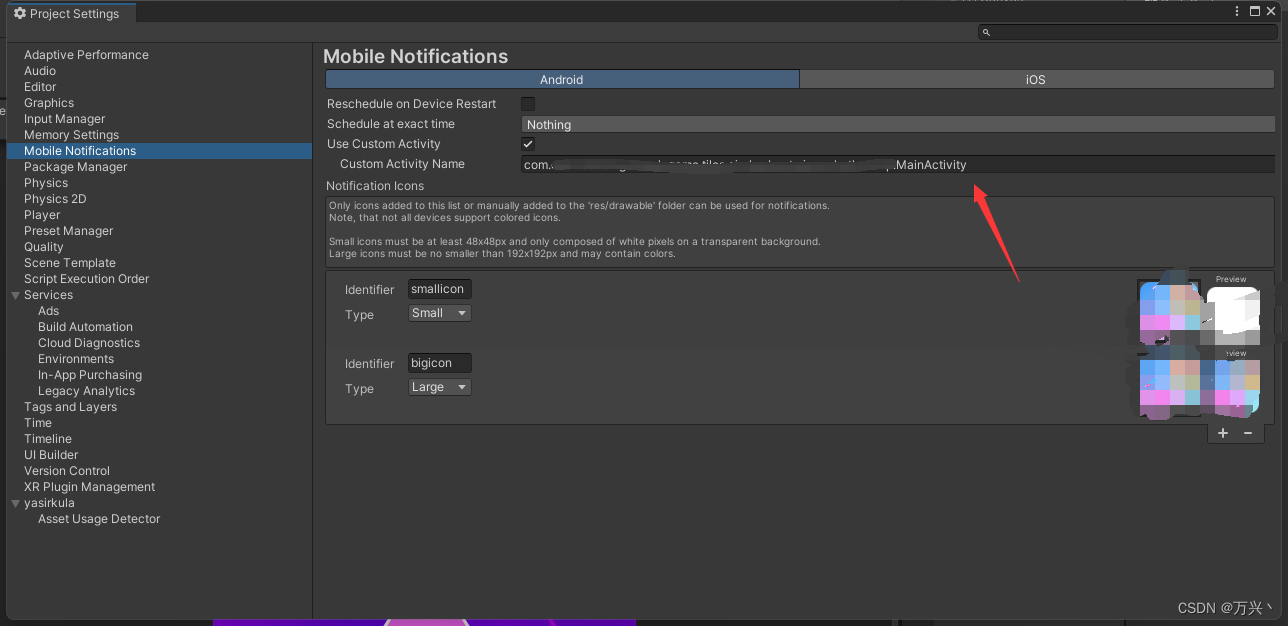
Unity Mobile Notifications推送问题
1.在部分机型点击通知弹窗进不去游戏 把这里改成自己的Activity 2.推送的时候没有横幅跟icon红点 主要是第一句话 注册的时候选项可以选择 defaultNotificationChannel new AndroidNotificationChannel(“default_channel”, “Default Channel”, “For Generic notifica…...
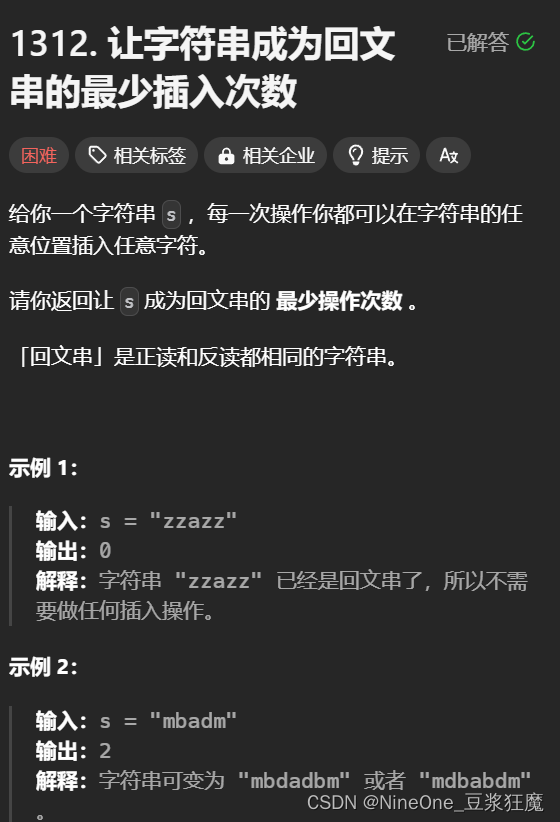
C++_回文串
目录 回文子串 最长回文子串 分割回文串 IV 分割回文串 II 最长回文子序列 让字符串成为回文串的最少插入次数 回文子串 647. 回文子串 思路,i j表示改范围内是否为回文串, ②倒着遍历是为了取出dp[i 1][j - 1] ③i j 只有一对,不会重复…...
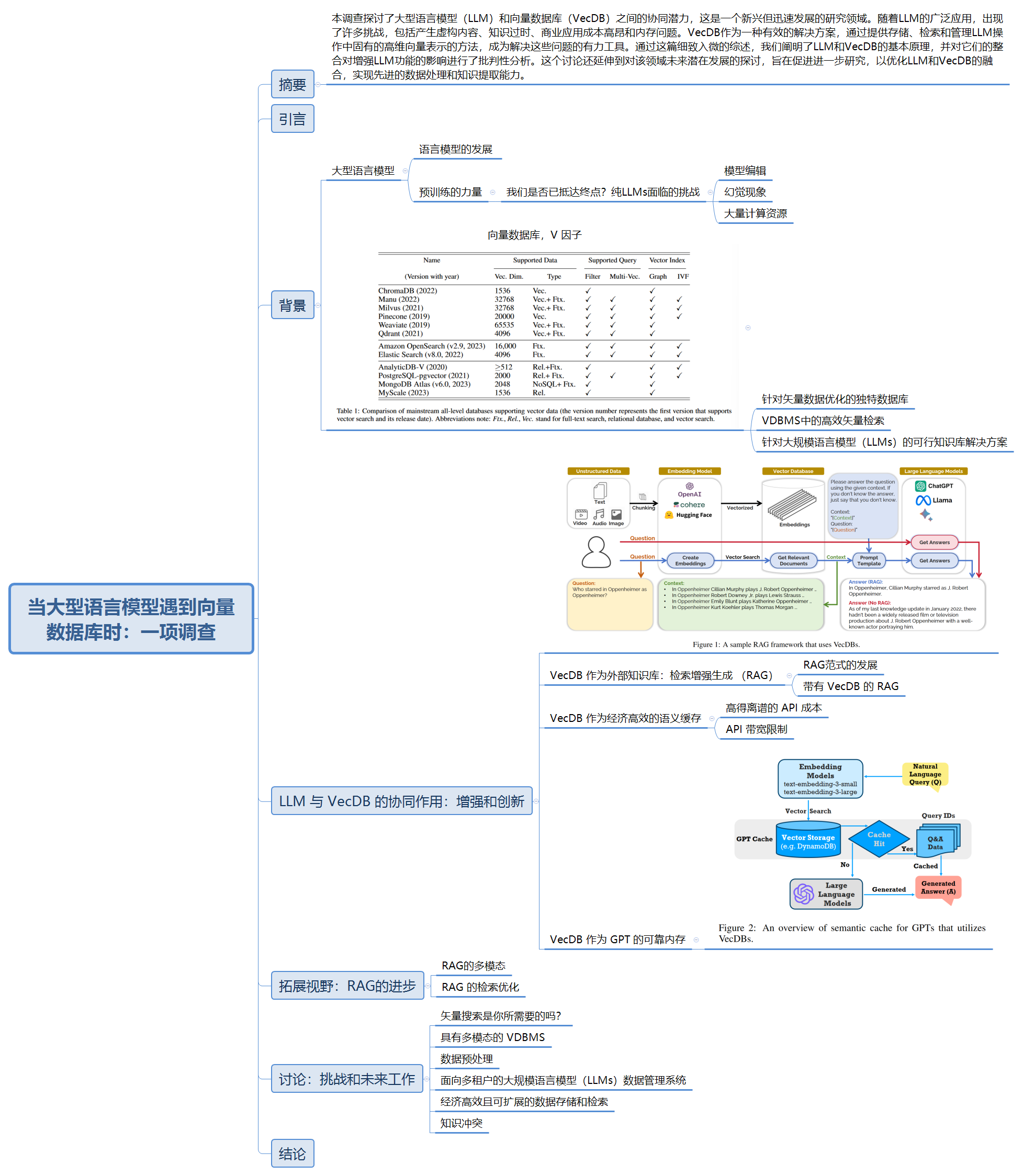
【阅读论文】When Large Language Models Meet Vector Databases: A Survey
摘要 本调查探讨了大型语言模型(LLM)和向量数据库(VecDB)之间的协同潜力,这是一个新兴但迅速发展的研究领域。随着LLM的广泛应用,出现了许多挑战,包括产生虚构内容、知识过时、商业应用成本高昂…...

兼职副业大揭秘:六个潜力满满的赚钱途径
亲爱的朋友,你对兼职副业充满好奇与期待,这非常好!在此,我将为你分享一些能够助你赚取额外收入的兼职副业建议。以下是六个颇具潜力的兼职副业方向,希望能为你的探索之路提供些许启发。 1,网络调查与市场洞…...
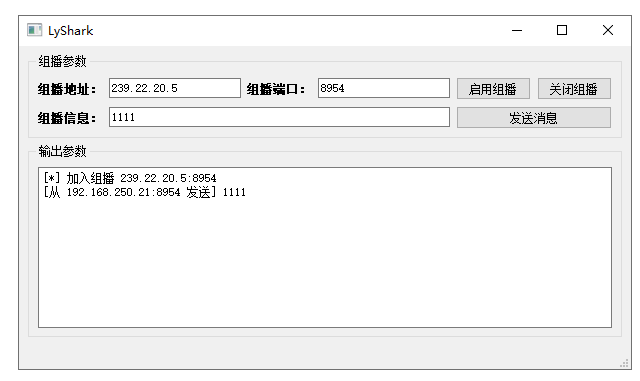
C++ Qt开发:QUdpSocket实现组播通信
Qt 是一个跨平台C图形界面开发库,利用Qt可以快速开发跨平台窗体应用程序,在Qt中我们可以通过拖拽的方式将不同组件放到指定的位置,实现图形化开发极大的方便了开发效率,本章将重点介绍如何运用QUdpSocket组件实现基于UDP的组播通信…...
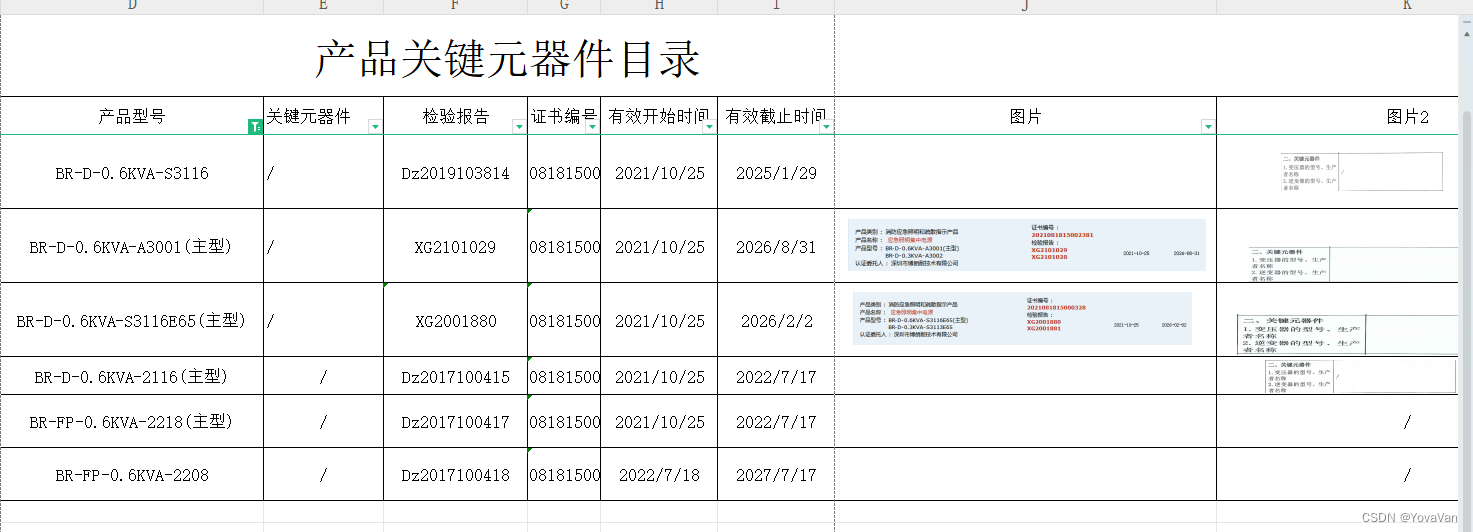
excel 表中有图片并在筛选特定行时,只显示该行的图片
建议:选中excel 表中某张图片,CtrlA,选中所有图片。再右键,在菜单中选设置对象格式 在属性里按下图设置, 生效之后,筛选某个产品的时候,就不会显示其他的不符合筛选条件的产品的图片了。...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...