算法系列--动态规划--⼦数组、⼦串系列(数组中连续的⼀段)(1)
💕"我们好像在池塘的水底,从一个月亮走向另一个月亮。"💕
作者:Mylvzi
文章主要内容:算法系列–动态规划–⼦数组、⼦串系列(数组中连续的⼀段)(1)
大家好,今天为大家带来的是
算法系列--动态规划--⼦数组、⼦串系列(数组中连续的⼀段)(1),这是动态规划新的一种题型
1.最⼤⼦数组和
链接:
https://leetcode.cn/problems/maximum-subarray/
分析:
动态规划的子数组问题和前缀和问题是不一样的,
子数组和这道题要求的是子数组和的最大值,我们的状态表示就是记录以i位置为结束的所有子数组的最大和,而前缀和只是一种快速求出区间和的方法,并没有表示最大和这种状态
关于求最大子数组和问题这道题,要注意状态表示的含义以i位置为结尾的所有子数组的最大和,也就是必须以i位置为结尾,那么此时的状态其实只有两种:
- 单独一个
- 前面的一堆 + 它本身
网上的很多推到状态方程的时候其实很容易让人误解,解释的也不清楚,他们进行状态的分类是根据dp[i - 1]的正负来推导dp[i]的,有的人可能想为什么不判断nums[i]的正负呢?
其实本质都一样,笔者觉得单纯通过形式来推到方程更容易理解一些
子串/子数组问题的一个经验的状态分类就是按照长度分类的,因为他们的状态表示都比较固定,都是以i位置为结束的最大xxxx
有的题目还比较恶心(尤其是关于子串的问题),对于相同的子串有时候还需要去重,就需要额外开一个数组来统计次数
本题的分析思路:

代码:
class Solution {public int maxSubArray(int[] nums) {int n = nums.length;int dp = 0;int max = -0x3f3f3f3f;// 将最大/小值设置为+-ox3f3f3f3f是一种经验for(int num : nums) {dp = Math.max(num,dp + num);// 填表max = Math.max(max,dp);// 更新最值}return max;}
}
2.环形⼦数组的最⼤和
链接:
https://leetcode.cn/problems/maximum-sum-circular-subarray/description/
分析:
本题是上题的一个变种,这里带环了,对于带环的问题,我们最常用的一个做法是想办法将其转化为线性的,对于本题我们可以采用分类讨论的思想
根据什么区分类讨论呢?往往是根据最后结果可能出现的形式去考虑,对于本题,最长的子数组和可能是两种情况
- 不带环,在区间内部
- 带环,跨越区间
对于情况1,就是最大子数组和的解法,对于情况2,可以转化为求区间内的最小值,那么最大值就是sum - min,最后返回情况1和情况2的最大值即可
下面是详细分析过程

代码:
class Solution {public int maxSubarraySumCircular(int[] nums) {// 创建dp表int n = nums.length;if(n == 1) return nums[0];int[] f = new int[n];int[] g = new int[n];// 初始化f[0] = g[0] = nums[0];int max = -0x3f3f3f3f;int min = 0x3f3f3f3f;int sum = nums[0];// 填表for(int i = 1; i < n; i++) {f[i] = Math.max(nums[i],f[i - 1] + nums[i]);g[i] = Math.min(nums[i],g[i - 1] + nums[i]);max = Math.max(max,f[i]);min = Math.min(min,g[i]);sum += nums[i];}// 返回值return sum == min ? max : Math.max(max,sum - min);}
}
3.乘积最⼤⼦数组
链接:
https://leetcode.cn/problems/maximum-product-subarray/
分析:
首先想到的状态表示就是以i位置为结尾子数组的最大乘积,但是根据这个状态表示去推到状态转移方程时发现只使用一个dp表无法表示所有的情况
- 当
nums[i] > 0,i位置的状态就是前一个位置的最大乘积 * nums[i] - 当
nums[i] < 0,此时无法通过dp[i - 1]来推到dp[i],因为一个负数 * 较大的数一定会变小,那么dp[i]存储的就是以i位置为结尾的子数组的最小乘积,这与我们的状态表示是矛盾的
既然当nums[i] < 0时,需要乘的是以i-1位置为结尾的子数组的最小乘积,那么我们就创建出一个dp表g[i]来表示最小乘积,以下是详细分析过程:
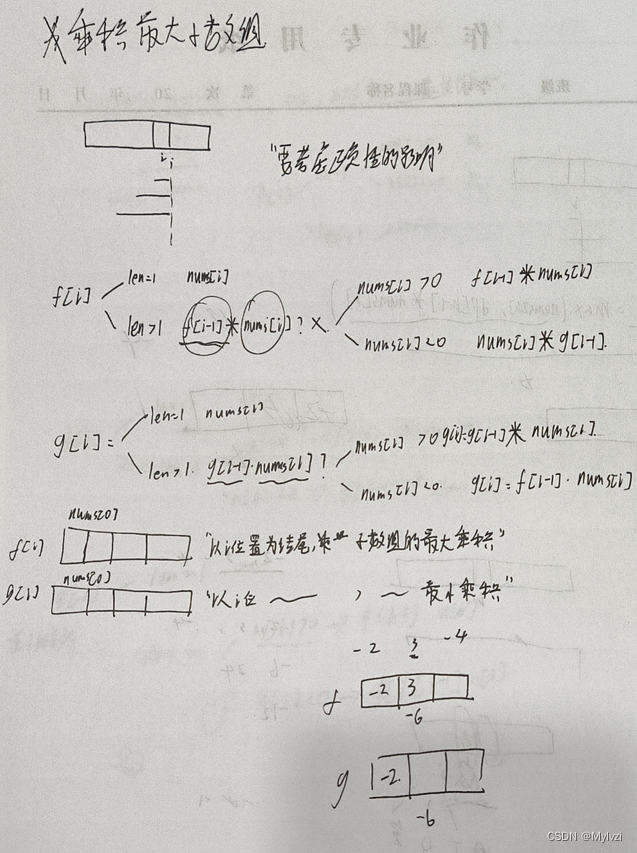
代码:
class Solution {public int maxProduct(int[] nums) {// 创建dp表int n = nums.length;int[] f = new int[n];int[] g = new int[n];// 初始化f[0] = g[0] = nums[0];int max = f[0];// 填表for(int i = 1; i < n; i++) {int t1 = 0, t2 = 0;if(nums[i] > 0) {f[i] = f[i - 1] * nums[i];g[i] = g[i - 1] * nums[i];}else {f[i] = g[i - 1] * nums[i];g[i] = f[i - 1] * nums[i];}f[i] = Math.max(nums[i],f[i]);g[i] = Math.min(nums[i],g[i]);max = Math.max(f[i],max);}return max;}
}
4.乘积为正数的最⻓⼦数组
链接:
https://leetcode.cn/problems/maximum-length-of-subarray-with-positive-product/description/
分析:
本题相较于上题有两个不同:
- 本题要求乘积必须为正数
- 本题求解的不是最大的乘积,而是乘积为正数的最长子数组
和上题一样,本题同样需要使用两个dp表来进行状态表示
f[i]:以i位置为结尾,乘积为正数的最大子数组长度g[i]:以i位置为结尾,乘积为负数的最大子数组长度
状态转移方程推导如下:
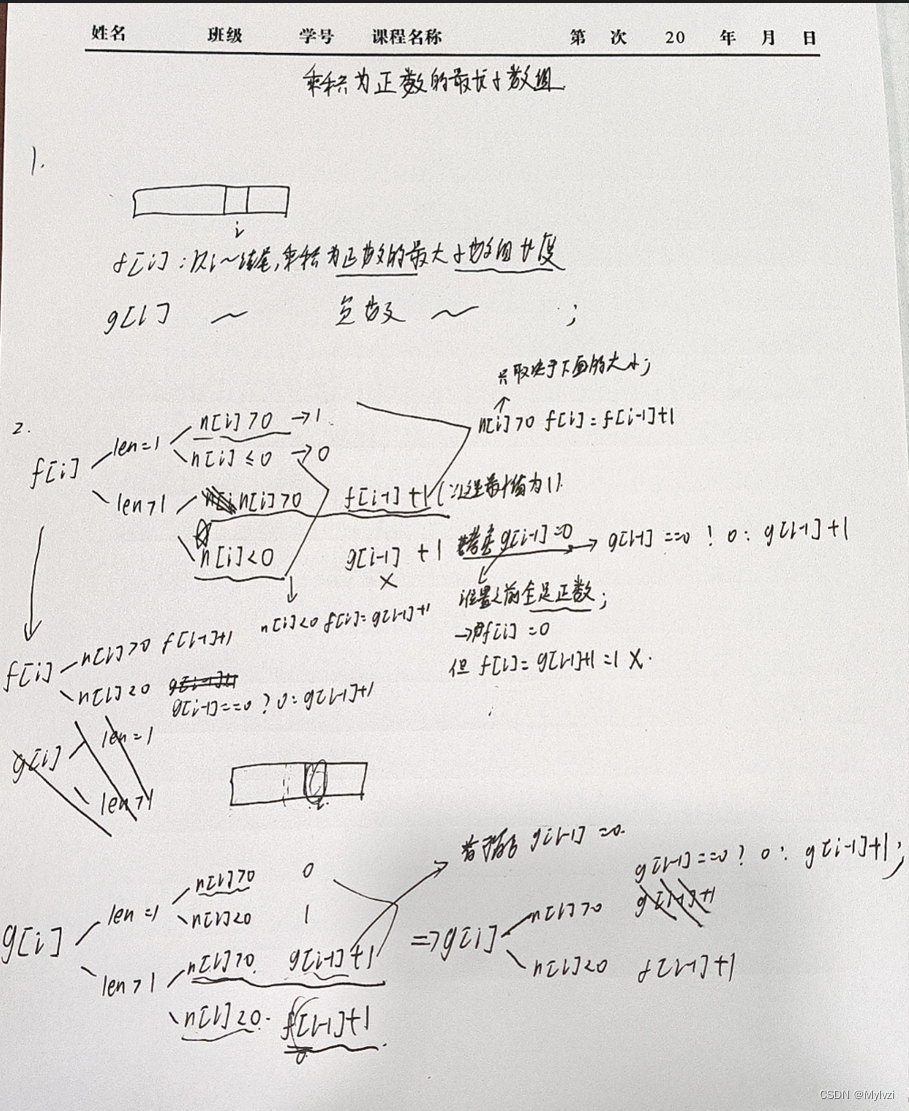
注意特殊情况:
- 当n[i] < 0时,
f[i] == g[i - 1] + 1,但是如果i位置之前全是正数,此时g[i - 1] == 0,那么f[i] == 0 + 1 = 1了,但是因为n[i] < 0,i位置的f[i]应该等于 0,因为所有的以i位置为结尾的子数组的乘积必然为负数
代码:
class Solution {public int getMaxLen(int[] nums) {int n = nums.length;// 1.创建dp表int[] f = new int[n];int[] g = new int[n];// 2.根据状态表示进行初始化f[0] = nums[0] > 0 ? 1 : 0;g[0] = nums[0] < 0 ? 1 : 0;int max = -0x3f3f3f3f;// 3.填表for(int i = 1; i < n; i++) {if(nums[i] > 0) {f[i] = f[i - 1] + 1;g[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;}else if(nums[i] < 0){f[i] = g[i - 1] == 0 ? 0 : g[i - 1] + 1;g[i] = f[i - 1] + 1;}else {f[i] = g[i] = 0;// 注意等于0相当于直接截断 要重新计数 从0开始}max = Math.max(f[i],max);// 更新长度}// 处理n == 1的情况return max == -0x3f3f3f3f ? f[0] : max;}
}
总结:
- 子数组问题最常用的一种状态表示就是
以i位置为结尾的xxxx - 在推导状态转移方程时,往往是根据
组成子数组的形态来分类讨论(单独一个还是和前面一堆组成子数组)
相关文章:

算法系列--动态规划--⼦数组、⼦串系列(数组中连续的⼀段)(1)
💕"我们好像在池塘的水底,从一个月亮走向另一个月亮。"💕 作者:Mylvzi 文章主要内容:算法系列–动态规划–⼦数组、⼦串系列(数组中连续的⼀段)(1) 大家好,今天为大家带来的是算法系…...

RESTful架构
RESTful架构中的URI设计与传统的URL设计有一些区别。让我通过具体的例子来解释一下: 传统的URL设计通常将操作和资源混合在一起,例如: 获取所有图书:GET /getBooks获取特定图书:GET /getBookById/{id}创建新图书&…...
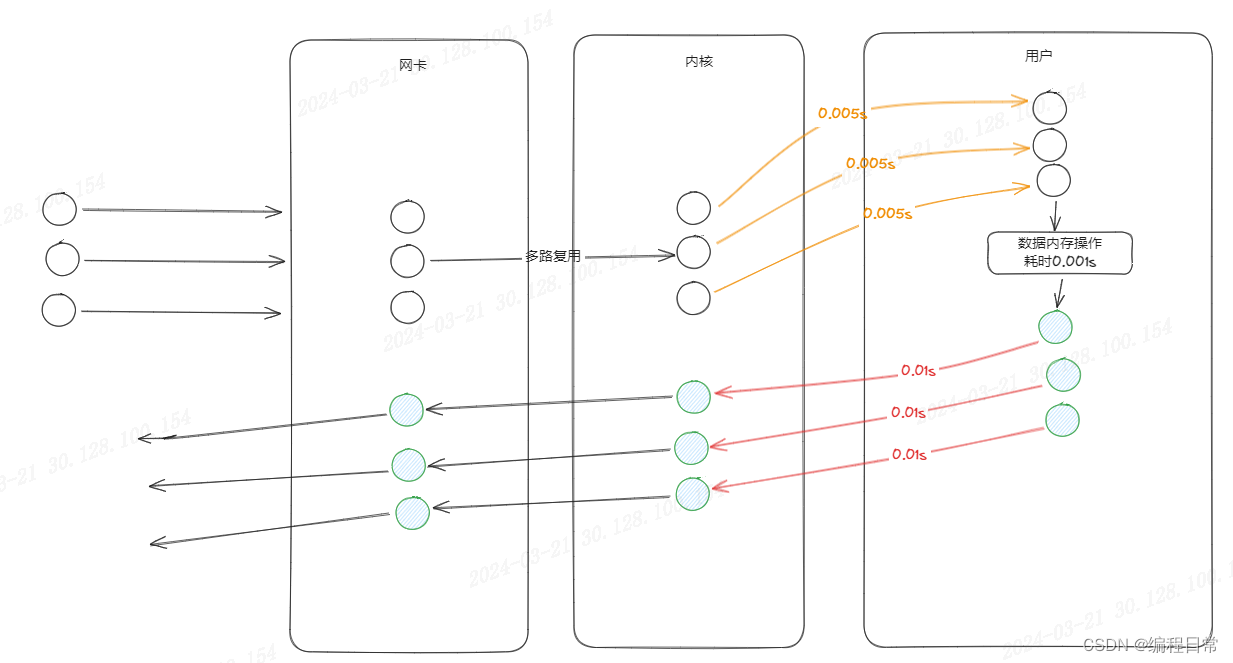
从IO操作与多线程的思考到Redis-6.0
IO操作->线程阻塞->释放CPU资源->多线程技术提升CPU利用率 在没有涉及磁盘操作和网络请求的程序中,通常不会出现线程等待状态。线程等待状态通常是由于线程需要等待某些事件的发生,比如I/O操作完成、网络请求返回等。如果程序只是进行计算或者简…...

MNN介绍、安装和编译
MNN是一个轻量级的深度学习推理框架,由阿里巴巴公司开发。它支持多种硬件平台,包括CPU、GPU和NPU,并提供高效、高性能的深度学习模型推理服务。下面是MNN的安装和编译步骤: 下载MNN源代码 在MNN的GitHub页面(https://g…...

【计算机图形学】AO-Grasp: Articulated Object Grasp Generation
对AO-Grasp: Articulated Object Grasp Generation的简单理解 文章目录 1. 做的事情2. AO-Grasp数据集2.1 抓取参数化和label标准2.2 语义和几何感知的抓取采样 3. AO-Grasp抓取预测3.1 预测抓取点3.2 抓取方向预测 4. 总结 1. 做的事情 引入AO-Grasp,grasp propo…...

「媒体宣传」财经类媒体邀约资源有哪些?-51媒体
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 财经类媒体邀约资源包括但不限于以下几类: 商业杂志和报纸:可以邀请如《财经》、《新财富》、《经济观察报》等主流商业杂志和报纸。这些媒体通常具有较强的品牌影…...

学习资料记录
http://interview.wzcu.com/Golang/%E4%BB%A3%E7%A0%81%E8%80%83%E9%A2%98.html map底层 https://zhuanlan.zhihu.com/p/616979764 go修养 https://www.yuque.com/aceld/golang/ga6pb1#4b19dba5 https://golang.dbwu.tech/performance/map_pre_alloc/ https://juejin.cn/pos…...

数据结构进阶篇 之 【二叉树】详细概念讲解(带你认识何为二叉树及其性质)
有朋自远方来,必先苦其心志,劳其筋骨,饿其体肤,空乏其身,鞭数十,驱之别院 一、二叉树 1、二叉树的概念 1.1 二叉树中组分构成名词概念 1.2 二叉树的结构概念 1.3 特殊的二叉树 2、二叉树的存储结构 …...

vue.js制作学习计划表案例
通俗易懂,完成“学习计划表”用于对学习计划进行管理,包括对学习计划进行添加、删除、修改等操作。 一. 初始页面效果展示 二.添加学习计划页面效果展示 三.修改学习计划完成状态的页面效果展示 四.删除学习计划 当学习计划处于“已完成”状态时&…...

nginx localtion 匹配规则
1、语法规则 语法规则:location[|~|^~*|^~]/uri/{… } 表示精确匹配,这个优先级也是最高的 ^~ 表示 uri 以某个常规字符串开头,理解为匹配 url 路径即可。 nginx 不对 url 做编码,因此请求为 /image/20%/aa,可以被规则^~ /imag…...

Git:分布式版本控制系统
目录 Git的特点和功能常见的功能和对应的命令 Git的特点和功能 Git是一个分布式版本控制系统,用于跟踪和管理项目的代码变更。它是由Linus Torvalds在2005年创建的,旨在管理Linux内核的开发。Git具有以下特点和功能: 分布式版本控制…...

[STL]priority_queue类及反向迭代器的模拟实现
🪐🪐🪐欢迎来到程序员餐厅💫💫💫 今日主菜: priority_queue类及反向迭代器 主厨:邪王真眼 主厨的主页:Chef‘s blog 所属专栏:c大冒险 向着c&…...

vue2 脚手架
安装 文档:https://cli.vuejs.org/zh/ 第一步:全局安装(仅第一次执行) npm install -g vue/cli 或 yarn global add vue/cli 备注:如果出现下载缓慢:请配置npm 淘宝镜像: npm config set regis…...

【OpenStack】OpenStack实战之开篇
目录 那么,OpenStack是什么?云又是什么?关于容器应用程序OpenStack如何适配其中?如何设置它?如何学会使用它?推荐超级课程: Docker快速入门到精通Kubernetes入门到大师通关课AWS云服务快速入门实战我的整个职业生涯到目前为止一直围绕着为离线或隔离网络设计和开发应用程…...

Python实现WebSocket通信
WebSocket是一种在单个TCP连接上进行全双工通信的协议,位于 OSI 模型的应用层。 与传统的HTTP请求-响应模型不同,WebSocket的最大特点就是,服务器可以主动向客户端推送信息,客户端也可以主动向服务器发送信息,实现实时性和互动性…...
MATLAB 自定义生成直线点云(详细介绍) (47)
MATLAB 自定义生成直线点云 (详细介绍)(47) 一、算法介绍二、具体步骤二、算法实现1.代码2.效果一、算法介绍 通过这里的直线生成方法,可以生成模拟直线的点云数据,并通过调整起点、终点、数量和噪声水平等参数来探索不同类型的直线数据。这种方法可以用于测试、验证和开…...
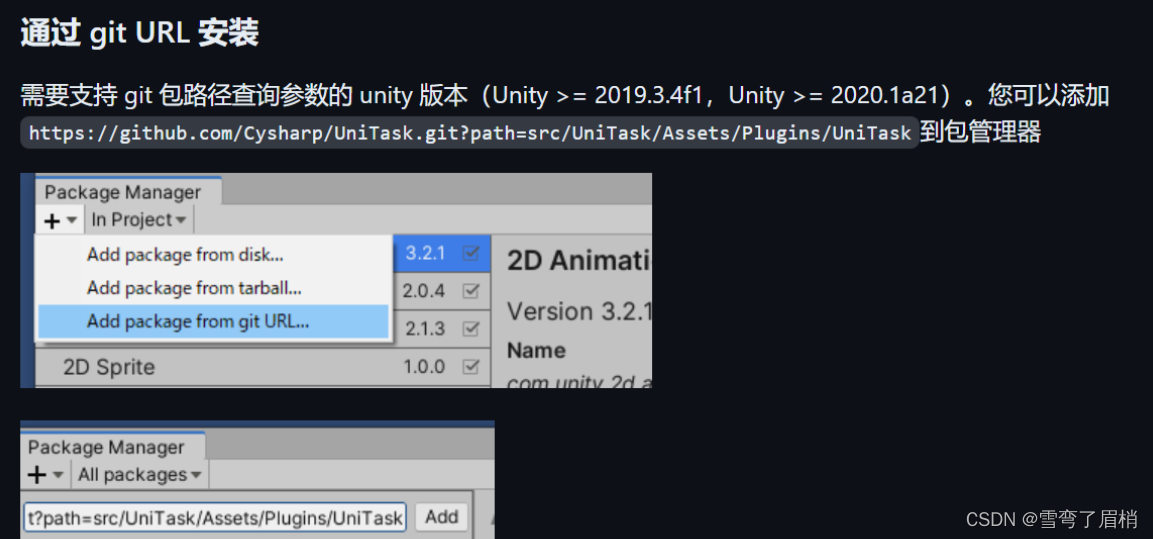
UniTask 异步任务
文章目录 前言一、UniTask是什么?二、使用步骤三、常用的UniTask API和示例1.编写异步方法2.处理异常3.延迟执行4.等待多个UniTask或者一个UniTas完成5.异步加载资源示例6.手动控制UniTask的完成状态7.UniTask.Lazy延迟任务的创建8.后台线程切换Unity主线程9.不要返…...
【git分支管理策略】如何高效的管理好代码版本
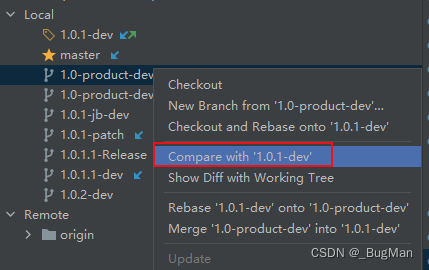
目录 1.分支管理策略 2.我用的分支管理策略 3.一些常见问题 1.分支管理策略 分支管理策略就是一些经过实践后总结出来的可靠的分支管理的办法,让分支之间能科学合理、高效的进行协作,帮助我们在整个开发流程中合理的管理好代码版本。 目前有两套Git…...

css的transition详解
CSS的transition属性是一个简写属性,用于设置四个过渡效果属性,以在元素的状态改变时创建平滑的动画效果。这四个属性分别是: transition-property: 定义应用过渡效果的CSS属性名称。当指定的CSS属性改变时,过渡效果将…...

agent利用知识来做规划:《KnowAgent: Knowledge-Augmented Planning for LLM-Based Agents》笔记
文章目录 简介KnowAgent思路准备知识Action Knowledge的定义Planning Path Generation with Action KnowledgePlanning Path Refinement via Knowledgeable Self-LearningKnowAgent的实验结果 总结参考资料 简介 《KnowAgent: Knowledge-Augmented Planning for LLM-Based Age…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...

