数学分析复习:振荡型级数的收敛判别
文章目录
- 振荡型级数的收敛判别
本篇文章适合个人复习翻阅,不建议新手入门使用
振荡型级数的收敛判别
直观上,振荡型级数说的是级数各项有正有负,求和的时候可以相互抵消,故可能收敛
命题:Abel求和公式
设复数列 { a k } k ≥ 1 \{a_k\}_{k\geq 1} {ak}k≥1 和 { b k } k ≥ 1 \{b_k\}_{k\geq 1} {bk}k≥1,则
∑ k = 1 n a k b k = S n b n + ∑ k = 1 n − 1 S k ( b k − b k + 1 ) \sum\limits_{k=1}^na_kb_k=S_nb_n+\sum\limits_{k=1}^{n-1}S_k(b_k-b_{k+1}) k=1∑nakbk=Snbn+k=1∑n−1Sk(bk−bk+1)
其中 S n = ∑ k = 1 n a k S_n=\sum\limits_{k=1}^na_k Sn=k=1∑nak 表示部分和
证明
只需将 a k a_k ak 替换为 S k − S k − 1 S_k-S_{k-1} Sk−Sk−1,然后合并同类项即可
注:该公式即为离散版本的分部积分公式
命题:Dirichlet判别法
设实数列 { a k } , { b k } \{a_k\},\{b_k\} {ak},{bk}, S n S_n Sn 表示 { a k } \{a_k\} {ak} 的部分和,若
- { b k } \{b_k\} {bk} 是单调数列且 lim k → ∞ b k = 0 \lim\limits_{k\to\infty}b_k=0 k→∞limbk=0
- 存在 M M M,使得对任意 n ≥ 1 n\geq 1 n≥1, ∣ S n ∣ ≤ M |S_n|\leq M ∣Sn∣≤M
则级数 ∑ k = 1 a k b k \sum\limits_{k=1}^{a_kb_k} k=1∑akbk 收敛
证明思路(级数的Cauchy收敛准则)
不妨假设 { b k } \{b_k\} {bk} 单调递减,由 abel 求和法,任取 m ≥ n m\geq n m≥n,有
∣ ∑ k = n + 1 m a k b k ∣ = ∣ ( S m b m − S n b n ) + ∑ k = n m − 1 S k ( b k − b k + 1 ) ∣ ≤ M ∣ b m − b n ∣ + ∣ M ∣ ∣ ∑ k = n m − 1 ( b k − b k + 1 ) ∣ = 2 M ( b n − b m ) < ε \begin{split} |\sum\limits_{k=n+1}^ma_kb_k|&=|(S_mb_m-S_nb_n)+\sum\limits_{k=n}^{m-1}S_k(b_k-b_{k+1})|\\ &\leq M|b_m-b_n|+|M||\sum\limits_{k=n}^{m-1}(b_k-b_{k+1})|\\ &=2M(b_n-b_m)<\varepsilon \end{split} ∣k=n+1∑makbk∣=∣(Smbm−Snbn)+k=n∑m−1Sk(bk−bk+1)∣≤M∣bm−bn∣+∣M∣∣k=n∑m−1(bk−bk+1)∣=2M(bn−bm)<ε
推论:Abel判别法
设实数列 { a k } , { b k } \{a_k\},\{b_k\} {ak},{bk},若
- { b k } \{b_k\} {bk} 单调有界
- 级数 ∑ k = 1 ∞ a k \sum\limits_{k=1}^{\infty}a_k k=1∑∞ak 收敛
则级数 ∑ k = 1 ∞ a k b k \sum\limits_{k=1}^{\infty}a_kb_k k=1∑∞akbk 收敛
证明思路
设 b = lim k → ∞ b k b=\lim\limits_{k\to\infty}b_k b=k→∞limbk,则有
∑ k = 1 ∞ a k b k = ∑ k = 1 ∞ a k ( b k − b ) + b ∑ k = 1 ∞ a k \sum\limits_{k=1}^{\infty}a_kb_k=\sum\limits_{k=1}^{\infty}a_k(b_k-b)+b\sum\limits_{k=1}^{\infty}a_k k=1∑∞akbk=k=1∑∞ak(bk−b)+bk=1∑∞ak
等号右端第一个级数用Dirichlet判别法立得
参考书:
- 《数学分析之课程讲义》清华大学数学系及丘成桐数学中心
- 《数学分析习题课讲义》谢惠民 恽自求 易法槐 钱定边 著
相关文章:

数学分析复习:振荡型级数的收敛判别
文章目录 振荡型级数的收敛判别 本篇文章适合个人复习翻阅,不建议新手入门使用 振荡型级数的收敛判别 直观上,振荡型级数说的是级数各项有正有负,求和的时候可以相互抵消,故可能收敛 命题:Abel求和公式 设复数列 { …...

阿里CICD流水线Docker部署,将阿里镜像私仓中的镜像部署到服务器中
文章目录 阿里CICD流水线Docker部署,将阿里镜像私仓中的镜像部署到服务器中一、CICD流水线的初步使用可以看我之前的两篇文章二、添加部署任务,进行Docker部署,创建一个阿里的试用主机1、选择主机部署,并添加服务主机2、创建免费体…...
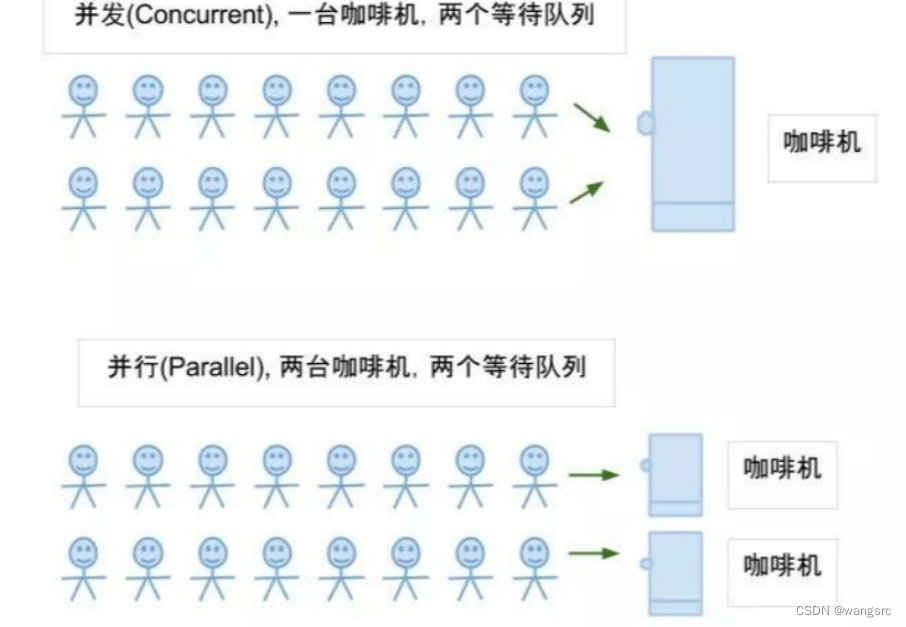
并发VS并行
参考文章 面试必考的:并发和并行有什么区别? 并发:一个人同时做多件事(射击游戏队友抢装备) 并行:多人同时处理同一件事(射击游戏敌人同时射击对方)...
 --- 进制A+B、网购、及格分数、最高分数、计算一元二次方程)
C语言经典例题(8) --- 进制A+B、网购、及格分数、最高分数、计算一元二次方程
文章目录 1.进制AB2.网购3.及格分数4.最高分数5.计算一元二次方程 1.进制AB 题目描述: 输入一个十六进制数a,和一个八进制数b,输出ab的十进制结果(范围-231~231-1)。 输入描述: 一行,一个十六…...
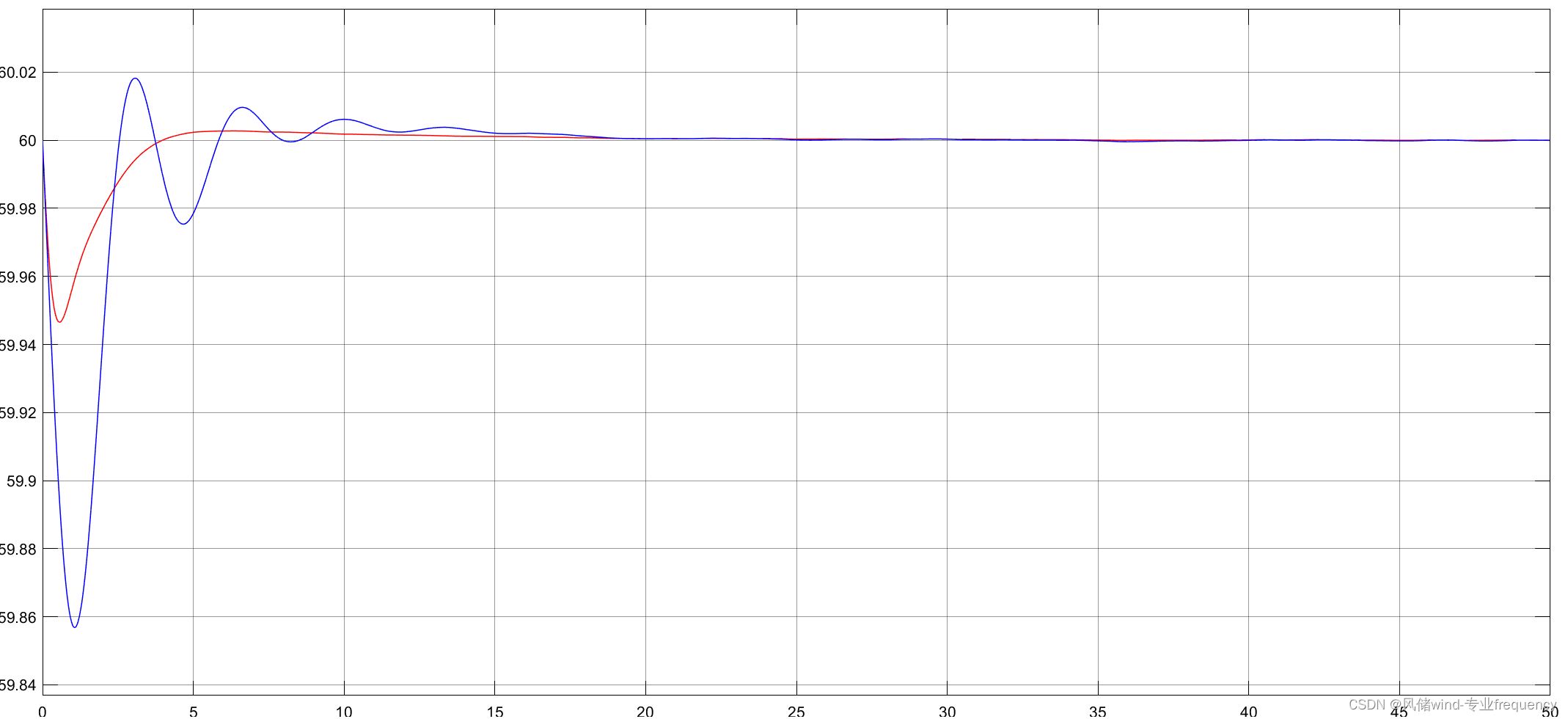
两区域二次调频风火机组,麻雀启发式算法改进simulink与matlab联合
区域1结果 区域2结果 红色曲线为优化后结果〔风火机组二次调频〕...

自动驾驶国际标准ISO文件
Coordinate system:Road vehicles — Vehicle dynamics and road-holding ability — Vocabulary...
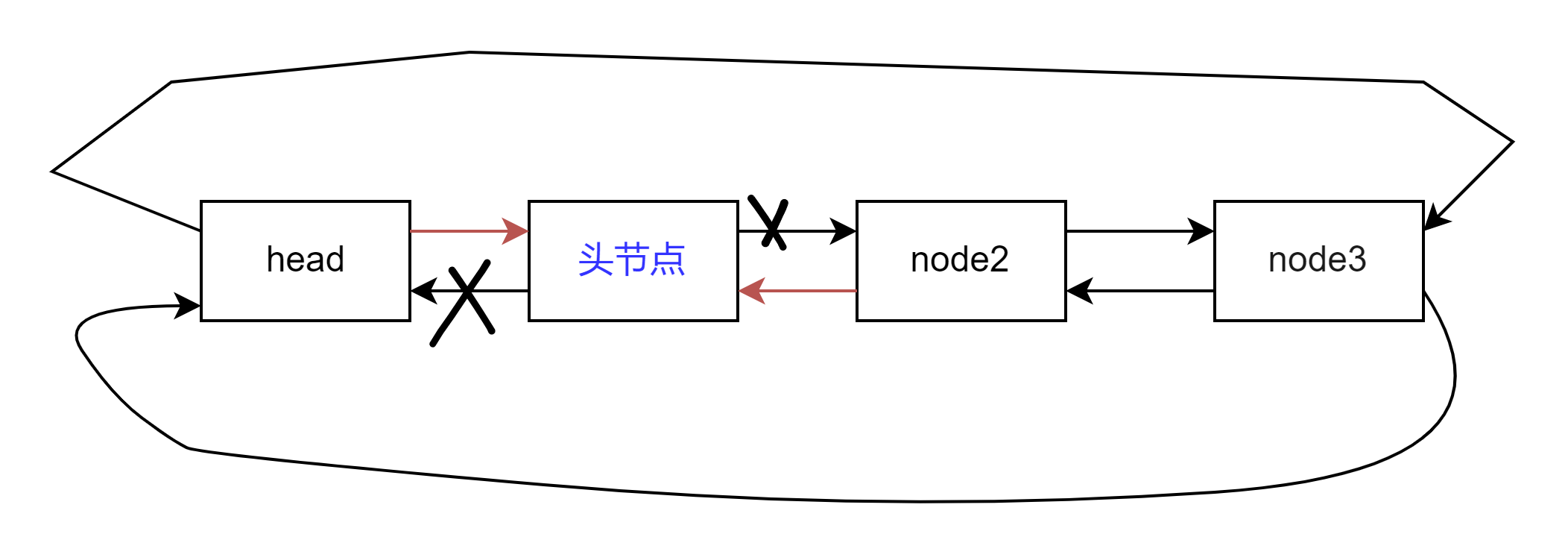
【数据结构】双向奔赴的爱恋 --- 双向链表
关注小庄 顿顿解馋๑ᵒᯅᵒ๑ 引言:上回我们讲解了单链表(单向不循环不带头链表),我们可以发现他是存在一定缺陷的,比如尾删的时候需要遍历一遍链表,这会大大降低我们的性能,再比如对于链表中的一个结点我们是无法直接…...

【Redis】高频面试题
提供五种常见的数据类型:String(字符串),Hash(哈希),List(列表),Set(集合)、Zset(有序集合) 文章目录 1、为什…...

数据分析基础
数据分析基础 1. 数据加载 使用 Pandas 库可以轻松地加载各种格式的数据,如 CSV、Excel、JSON 等。 import pandas as pd# 从 CSV 文件加载数据 data pd.read_csv(‘data.csv’). 2. 数据探索 一旦数据加载完成,我们可以开始对数据进行探索性分析&a…...

ffmpeg把一个平面视频,做成左右平面视频
要使用FFmpeg将单个平面视频转换为左右(或称为并排)3D格式的视频,你可以使用FFmpeg的filter_complex功能来实现。这种类型的视频通常用于3D视觉效果,其中同一画面的两个版本并排放置,每个版本略有不同的视角࿰…...
Docker搭建LNMP环境实战(02):Win10下安装VMware
实战开始,先安装 VMware 虚拟机。话不多说,上手就干! 1、基本环境检查 1.1、本机Bios是否支持虚拟化 进入:任务管理器- 性能,查看“虚拟化”是否启用,如果已启用,则满足要求,如果未…...
苍穹外卖笔记
苍穹外卖 DAY01nginx反向代理MD5加密yapi进行接口导入Swagger介绍 DAY02新增员工需求分析和设计写相关代码测试(1. 后端文档测试 2. 前后端联调代码完善 员工分页查询DAY01 02涉及到的知识 DAY03阿里云OSS事务注解 Transactional DAY01 nginx反向代理 MD5加密 拓展࿱…...
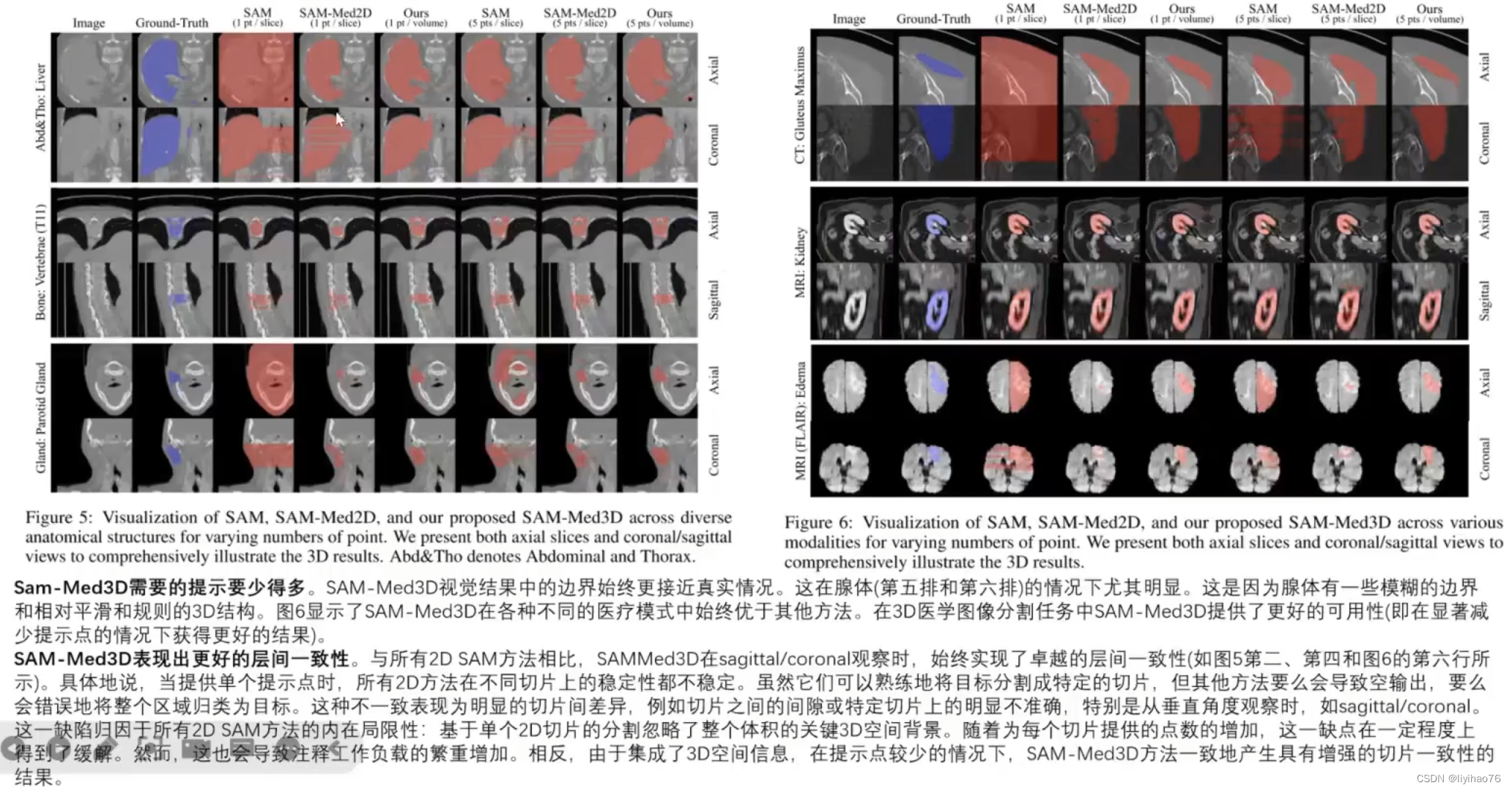
[医学分割大模型系列] (3) SAM-Med3D 分割大模型详解
[医学分割大模型系列] -3- SAM-Med3D 分割大模型解析 1. 特点2. 背景3. 训练数据集3.1 数据集收集3.2 数据清洗3.3 模型微调数据集 4. 模型结构4.1 3D Image Encoder4.2 3D Prompt Encoder4.3 3D mask Decoder4.4 模型权重 5. 评估5.1 评估数据集5.2 Quantitative Evaluation5.…...

【React】React中将 Props 传递给组件
当使用 React 时,props 是组件之间传递数据的主要方式。以下是针对您提到的五个问题的详细解答: 1. 如何向组件传递 props 在父组件中,你可以通过组件标签的属性(attributes)将 props 传递给子组件。这些属性在子组件…...

JOL工具查看java对象布局
JOL(Java Object Layout)是一个用于分析Java对象在Java虚拟机(JVM)中内存布局的小工具包。以下是如何使用JOL查看Java对象布局的步骤示例: Maven项目中添加依赖: 首先,在Maven项目中引入JOL工…...

Rust 实战练习 - 3. 文件系统,权限,读写,路径组合,time
目标: 文件系统,遍历目录路径的使用权限和文件属性时间time use std::{env, fmt::Debug, os::unix::fs::{MetadataExt, PermissionsExt}, path::{Path, PathBuf}, time::SystemTime};fn main() {// 时间处理// 除Duration和SystemTime外,标准库没有时间…...

既有理论深度又有技术细节——深度学习计算机视觉
推荐序 我曾经试图找到一本既有理论深度、知识广度,又有技术细节、数学原理的关于深度学习的书籍,供自己学习,也推荐给我的学生学习。虽浏览文献无数,但一直没有心仪的目标。两周前,刘升容女士将她的译作《深度学习计…...
:用 Temporal Table DDL 实现基于处理时间的关联)
Flink Temporal Join 系列 (2):用 Temporal Table DDL 实现基于处理时间的关联
本文要演示的是:使用 Temporal Table DDL 定义被关联表(维表),然后基于主动关联表(事实表)的“处理时间”去进行Temporal Join(关联时间维度上对应版本的维表数据)。该演示涉及三个要点: 被关联的表(维表)是用 Temporal Table DDL 形式定义,必须是一张时态表(版本…...
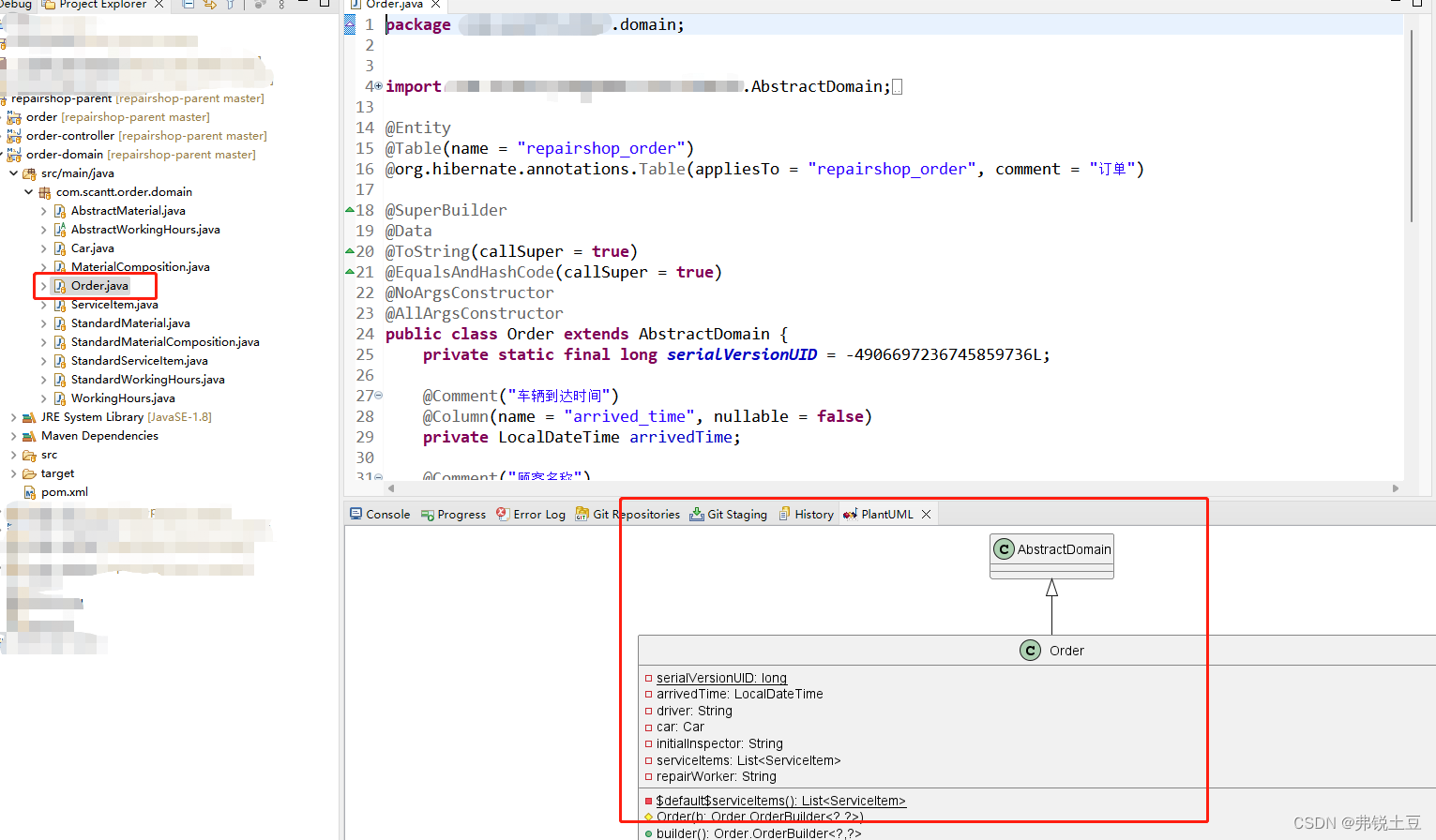
eclipse中使用PlantUML plugin查看对象关系
一.背景 公司安排的带徒弟任务,给徒弟讲了如何设计对象。他们的思维里面都是单表增删改查,我的脑海都是一个个对象,他们相互关系、各有特色本事。稳定的结构既能满足外部功能需求,又能在需求变更时以最小代价响应。最大程度的记录…...

HCIP的学习(4)
GRE和MGRE VPN---虚拟专用网络。指依靠ISP(运营商)或其他公有网络基础设施上构建的专用的安全数据通信网络。该网络是属于逻辑上的。 核心机制—隧道机制(封装技术) GRE—通用路由封装 三层隧道技术,并且是属于…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
