线性代数基础概念和在AI中的应用
基本概念
线性代数是数学的一个分支,专注于向量、向量空间(也称为线性空间)、线性变换和矩阵的研究。这些概念在数据科学、人工智能、工程学和物理学等多个领域都有广泛应用。以下是这些基本概念的详细解释和它们在数据处理和AI中的应用。
向量
- 基本概念:向量是具有大小(magnitude)和方向的量,可以在多维空间中表示。在数据科学中,向量常用来表示数据点或特征。
- 应用:在AI中,向量用于表示观测数据、特征、状态等。例如,在自然语言处理(NLP)中,词汇可以通过词向量来表示,反映不同词汇之间的语义相似性。
向量空间(线性空间)
- 基本概念:向量空间是一组向量的集合,这些向量满足加法和标量乘法的封闭性。向量空间为我们提供了一个框架,用于研究向量的线性组合。
- 应用:在机器学习中,不同的特征空间可以表示为不同的向量空间,算法会在这些空间中寻找数据之间的线性关系或模式。
线性变换
- 基本概念:线性变换是一种特殊的函数,它将一个向量空间中的向量映射到另一个向量空间,同时保持向量加法和标量乘法的操作。矩阵是线性变换的一种表示。
- 应用:在AI中,线性变换常用于数据变换和特征提取。例如,在深度学习中,神经网络的每一层可以视为一种线性变换,用于从数据中提取高级特征。
矩阵
- 基本概念:矩阵是一个由行和列组成的矩形数组,用于表示向量和线性变换。矩阵运算,包括矩阵的加法、乘法、转置和逆等,是线性代数的核心内容。
- 应用:矩阵在AI中的应用极为广泛,从简单的数据表示到复杂的神经网络计算。例如,神经网络的权重可以表示为矩阵,神经网络的前向传播和反向传播算法本质上是对这些矩阵进行运算。
特征值和特征向量
- 基本概念:对于给定的矩阵A,如果存在一个标量λ和一个非零向量v,使得Av = λv,那么λ称为A的一个特征值,v称为对应于λ的特征向量。
- 应用:特征值和特征向量在数据分析和机器学习中有重要应用,如主成分分析(PCA)就是通过寻找数据矩阵的特征值和特征向量来识别数据中最重要的特征。
通过掌握这些线性代数的基本概念,你将能够更好地理解和实施AI算法,尤其是那些涉及到大规模数据处理和复杂数学计算的算法。线性代数提供了一种强大的语言和工具,用于表述和解决数据科学和人工智能中的问题。
在AI中的应用
向量和矩阵运算
线性代数是AI特别是在机器学习和深度学习中不可或缺的数学工具。向量和矩阵运算是线性代数中最核心的部分,它们在AI的多个方面都有广泛应用。以下是这些概念在AI中应用的详细解释:
数据表示
- 向量:在AI中,向量常用来表示数据点或特征。例如,在自然语言处理(NLP)中,一个词可以通过一个向量(词向量)来表示,这个向量捕捉了词的语义特征。在图像识别中,一张图像可以展平为一个长向量,其元素表示图像中的像素值。
- 矩阵:矩阵用来表示多个数据点或多个特征。例如,一个数据集可以表示为一个矩阵,其中每一行代表一个数据点,每一列代表一个特征。这使得可以同时对多个数据点进行运算,大大提高了计算效率。
处理图像数据
- 在计算机视觉中,图像通常被表示为二维(灰度图像)或三维(彩色图像)矩阵,其中矩阵中的元素表示像素值。线性代数的矩阵运算允许我们进行图像处理操作,如旋转、缩放、平移和滤波等。深度学习模型,如卷积神经网络(CNN),进一步利用这些原理来识别和分类图像中的对象。
训练深度学习模型
- 权重和偏置:深度学习模型中的神经网络包含大量的权重和偏置,这些可以表示为矩阵和向量。在训练过程中,模型通过调整这些权重和偏置来学习数据的特征。
- 前向传播:计算输入数据通过神经网络的输出。这个过程涉及到大量的矩阵和向量乘法,以及线性变换和激活函数的应用。
- 反向传播:一种用于训练神经网络的算法,通过计算损失函数关于网络参数(权重和偏置)的梯度来更新这些参数。这个过程中大量使用了微分和线性代数的概念,包括矩阵的导数。
优化算法
- 大多数机器学习算法包括一个优化过程,旨在最小化或最大化某个目标函数(如损失函数)。线性代数在这些优化算法中扮演关键角色,尤其是在梯度下降等算法中,它需要计算目标函数相对于模型参数的梯度,这个梯度是通过矩阵和向量运算得到的。
总之,线性代数不仅为AI提供了一种强大的方式来表示和处理数据,还是构建和训练复杂模型所需计算的基础。理解和掌握向量和矩阵运算对于在AI领域取得成功至关重要。
特征值和特征向量
特征值和特征向量是线性代数中的重要概念,它们在数据分析、机器学习、物理学等多个领域有着广泛的应用。特别是在降维技术和优化问题中,它们扮演着关键的角色。
特征值和特征向量的定义

主成分分析(PCA)
主成分分析(PCA)是一种常用的数据降维技术,它通过线性变换将数据转换到新的坐标系统中,使得在新坐标系统的第一坐标轴上的数据方差最大(即第一个主成分),第二坐标轴上的数据方差次之,依此类推。PCA的目标是减少数据集的维度,同时保留数据集中最重要的方差结构。
在PCA中,数据的协方差矩阵(或相关矩阵)的特征值和特征向量有着特别的意义:
- 特征向量:协方差矩阵的特征向量指示了数据的主成分的方向。
- 特征值:每个特征值表示了其对应的特征向量方向上数据的方差量。特征值越大,表示那个方向上的数据变异(信息)越多。
通过选择最大的几个特征值对应的特征向量,我们可以将数据投影到由这些特征向量构成的较低维度空间中,从而实现降维。
优化问题
在优化问题中,特征值和特征向量也扮演着重要的角色。例如,在求解最优化问题时,我们常常需要找到函数的最大值或最小值。如果优化的目标函数可以通过矩阵表示,那么该矩阵的特征值可以帮助我们判断优化问题的性质(如凸性)和找到最优解的方向。
总结
特征值和特征向量提供了一种强大的工具,用于理解和处理线性变换。在PCA等数据降维技术中,它们帮助我们识别并保留数据中最重要的信息。在优化问题中,它们有助于我们理解问题的结构和解的性质。掌握特征值和特征向量的概念,对于进行高效的数据分析和解决复杂的数学问题至关重要。
奇异值分解(SVD)和主成分分析(PCA)
奇异值分解(SVD)和主成分分析(PCA)是两种强大的线性代数工具,广泛应用于数据分析、机器学习、图像处理等领域。它们都可以用于数据降维、特征提取、数据压缩和去噪,以及发现数据中的模式和结构。虽然SVD和PCA都可以达到相似的目的,但它们的出发点和计算方法有所不同。
奇异值分解(SVD)
定义:

应用:
- 数据压缩:通过保留最大的几个奇异值(和相应的奇异向量),可以近似重建原始数据矩阵,实现数据压缩。
- 去噪:奇异值较小的成分通常对应于噪声或不重要的信息,去除这些成分可以去噪。
- 特征提取:SVD可以揭示数据的内在结构,通过分析奇异值和奇异向量,可以发现数据中的模式和关系。
主成分分析(PCA)
定义: 主成分分析是一种统计方法,通过正交变换将可能相关的变量转换为一组线性不相关的变量,这些新的变量称为主成分。主成分是原始数据在新坐标系下的表示,第一主成分具有最大的方差(信息量),第二主成分次之,以此类推。
应用:
- 降维:通过选择包含大部分方差的前几个主成分,可以减少数据集的维度,同时保留最重要的信息。
- 数据可视化:通过将数据投影到前两个或三个主成分构成的空间,可以可视化高维数据。
- 特征提取:PCA能够揭示数据中的主要变动方向,有助于理解数据的内在结构。
SVD与PCA的关系
SVD和PCA紧密相关。实际上,PCA可以通过对数据矩阵的协方差矩阵进行奇异值分解来实现。PCA的主成分方向对应于SVD分解中矩阵V的列向量,即右奇异向量。而PCA的主成分得分可以通过奇异值和左奇异向量的乘积得到。
总之,SVD和PCA都是处理和分析大规模数据集的有力工具。它们通过提取数据的关键特征和结构,帮助我们更好地理解和利用数据。
相关文章:

线性代数基础概念和在AI中的应用
基本概念 线性代数是数学的一个分支,专注于向量、向量空间(也称为线性空间)、线性变换和矩阵的研究。这些概念在数据科学、人工智能、工程学和物理学等多个领域都有广泛应用。以下是这些基本概念的详细解释和它们在数据处理和AI中的应用。 …...
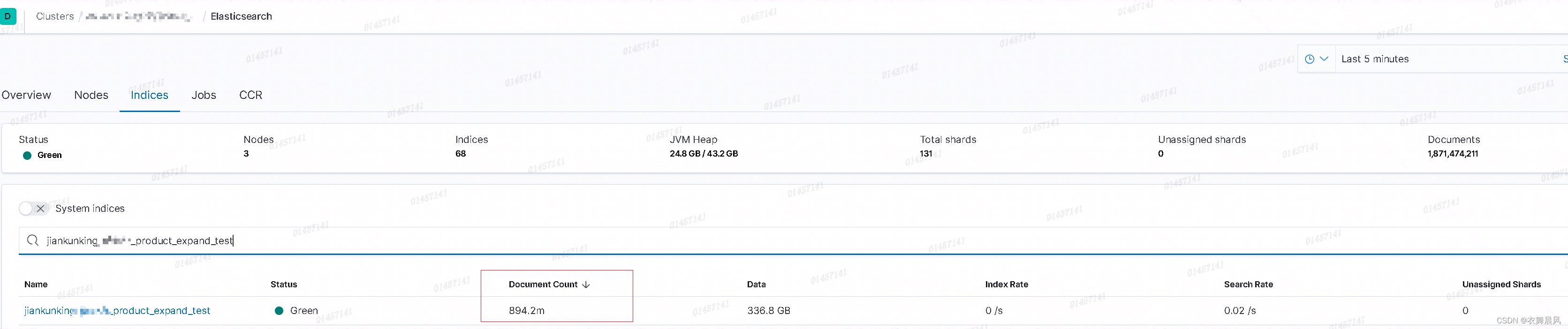
elasticsearch _cat/indices docs.count is different than <index>/_count
今天遇到一个问题,kibana中看到文档数与下面语句查询到的不同 GET /_cat/count/jiankunking_xxxxx_product_expand_test?v GET /jiankunking_xxxxx_product_expand_test/_search?track_total_hitstrue语句查询结果 epoch timestamp count 1711433785 06:16…...

关系型数据库mysql(7)sql高级语句
目录 一.MySQL常用查询 1.按关键字(字段)进行升降排序 按分数排序 (默认为升序) 按分数升序显示 按分数降序显示 根据条件进行排序(加上where) 根据多个字段进行排序 编辑 2.用或(or&…...

计算机网络——网络基础1
网络基础一 1.初识网络 网卡也是一种文件,所以对于网络的编程也是一种文件操作; 早期由于不同的计算机之间要根据数据进行协作,但是计算机之间是独立的,所以使用了光驱或者软盘之类的进行协作;对于将计算机连…...

ERDUnet: An Efficient Residual Double-codingUnet for Medical Image Segmentation
ERDUnet:一种用于医学图像分割的高效残差双编码单元 摘要 医学图像分割在临床诊断中有着广泛的应用,基于卷积神经网络的分割方法已经能够达到较高的准确率。然而,提取全局上下文特征仍然很困难,而且参数太大,无法临床应用。为此,我们提出了一种新的网络结构来改进传统的…...

vue响应式基础
声明响应式状态 ref() 在组合式 API 中,推荐使用 ref() 函数来声明响应式状态: import { ref } from vueconst count ref(0) ref() 接收参数,并将其包裹在一个带有 .value 属性的 ref 对象中返回: const count ref(0)c…...
每天上万简历,录取不到1%!阿里腾讯的 offer 都给了哪些人?
三月天杨柳醉春烟~正是求职好时节~ 与去年秋招的冷淡不同,今年春招市场放宽了许多,不少企业纷纷抛出橄榄枝,各大厂的只差把“缺人”两个字写在脸上了。 字节跳动技术方向开放数10个类型岗位,研发需求占比60%,非研发新增…...

外包干了20天,技术退步明显.......
先说一下自己的情况,大专生,21年通过校招进入杭州某软件公司,干了接近2年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落! 而我已经在一个企业干了2年的功能测试…...
4核8G云服务器,阿里云要多少钱?
阿里云4核8G服务器优惠价格955元一年,配置为ECS通用算力型u1实例(ecs.u1-c1m2.xlarge)4核8G配置、1M到3M带宽可选、ESSD Entry系统盘20G到40G可选,CPU采用Intel(R) Xeon(R) Platinum处理器,阿里云活动链接 aliyunfuwuq…...

数学分析复习:振荡型级数的收敛判别
文章目录 振荡型级数的收敛判别 本篇文章适合个人复习翻阅,不建议新手入门使用 振荡型级数的收敛判别 直观上,振荡型级数说的是级数各项有正有负,求和的时候可以相互抵消,故可能收敛 命题:Abel求和公式 设复数列 { …...

阿里CICD流水线Docker部署,将阿里镜像私仓中的镜像部署到服务器中
文章目录 阿里CICD流水线Docker部署,将阿里镜像私仓中的镜像部署到服务器中一、CICD流水线的初步使用可以看我之前的两篇文章二、添加部署任务,进行Docker部署,创建一个阿里的试用主机1、选择主机部署,并添加服务主机2、创建免费体…...
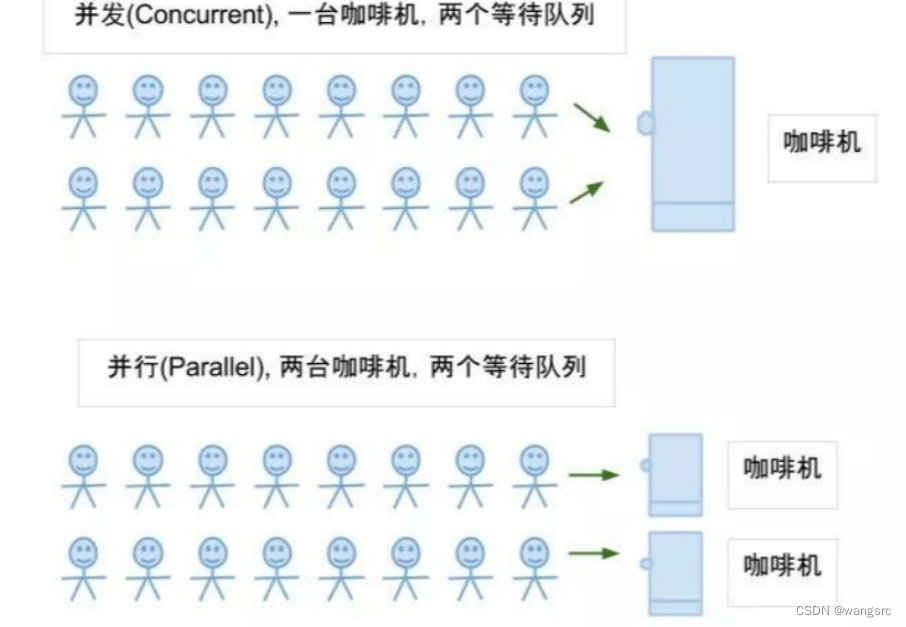
并发VS并行
参考文章 面试必考的:并发和并行有什么区别? 并发:一个人同时做多件事(射击游戏队友抢装备) 并行:多人同时处理同一件事(射击游戏敌人同时射击对方)...
 --- 进制A+B、网购、及格分数、最高分数、计算一元二次方程)
C语言经典例题(8) --- 进制A+B、网购、及格分数、最高分数、计算一元二次方程
文章目录 1.进制AB2.网购3.及格分数4.最高分数5.计算一元二次方程 1.进制AB 题目描述: 输入一个十六进制数a,和一个八进制数b,输出ab的十进制结果(范围-231~231-1)。 输入描述: 一行,一个十六…...
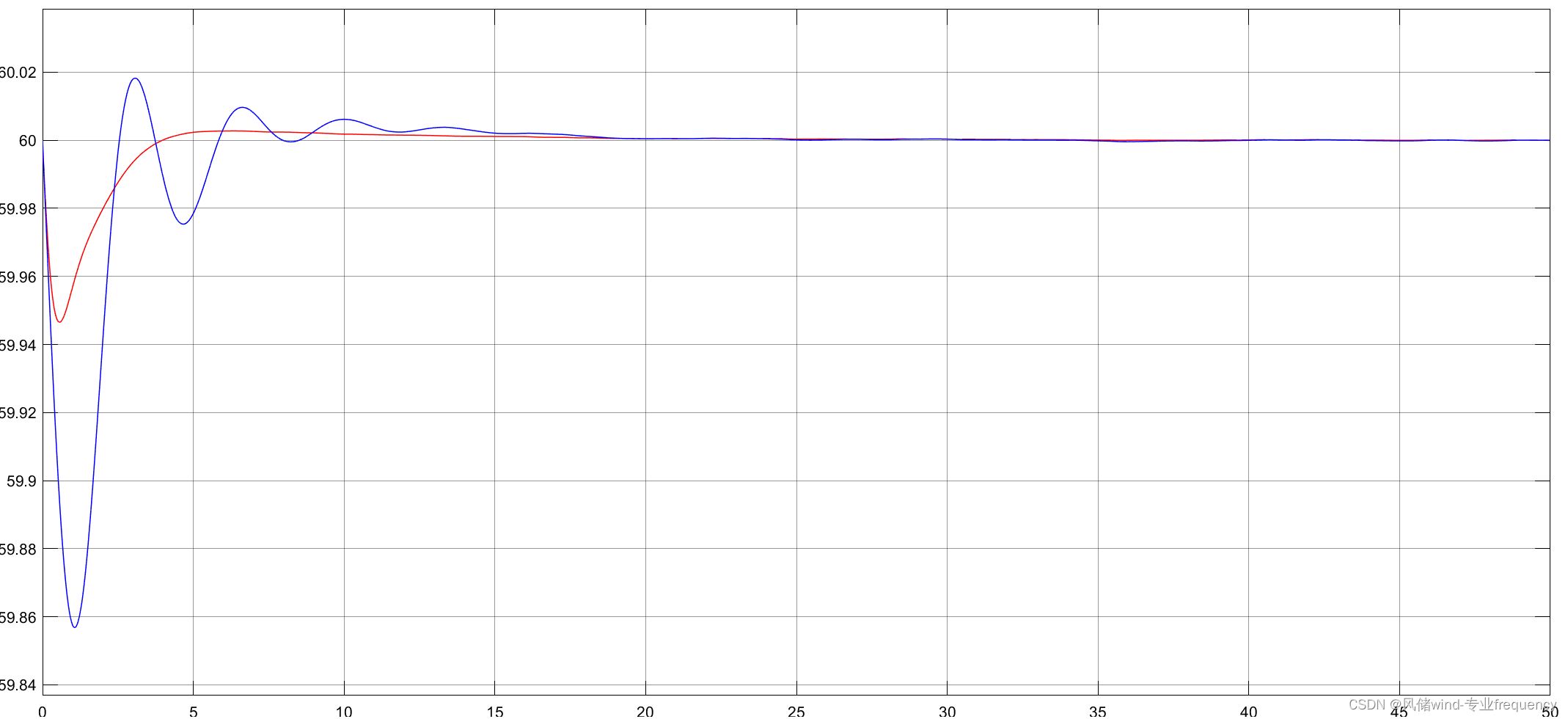
两区域二次调频风火机组,麻雀启发式算法改进simulink与matlab联合
区域1结果 区域2结果 红色曲线为优化后结果〔风火机组二次调频〕...

自动驾驶国际标准ISO文件
Coordinate system:Road vehicles — Vehicle dynamics and road-holding ability — Vocabulary...
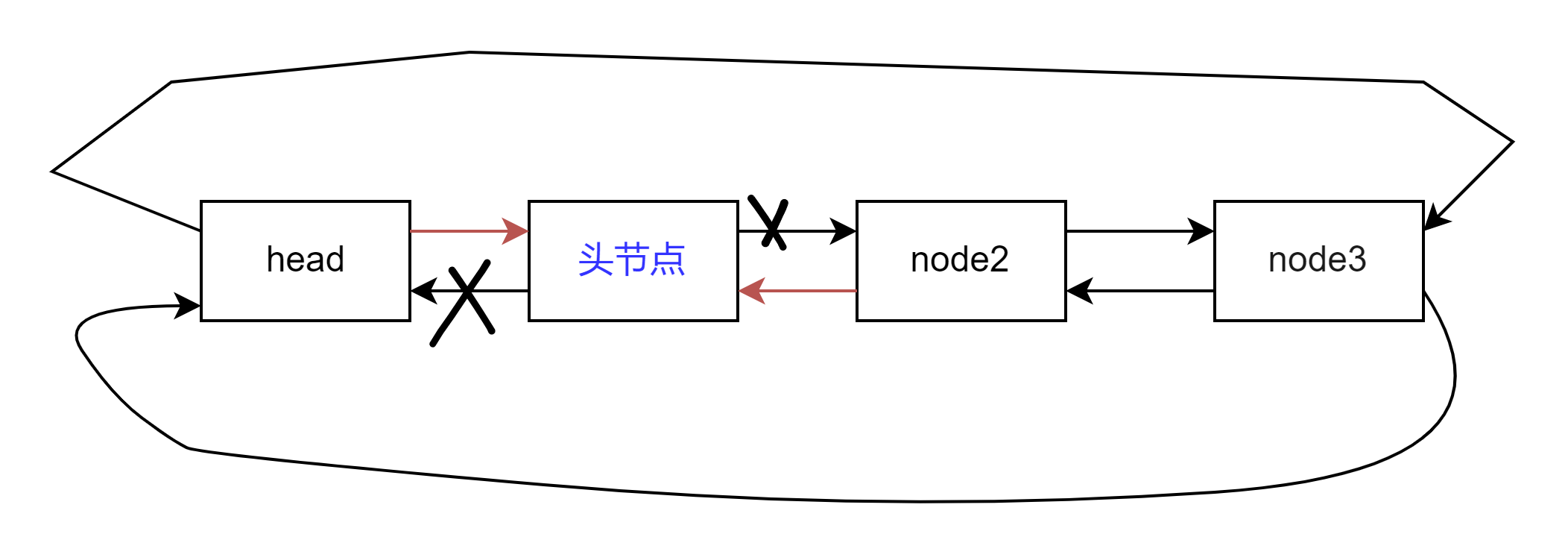
【数据结构】双向奔赴的爱恋 --- 双向链表
关注小庄 顿顿解馋๑ᵒᯅᵒ๑ 引言:上回我们讲解了单链表(单向不循环不带头链表),我们可以发现他是存在一定缺陷的,比如尾删的时候需要遍历一遍链表,这会大大降低我们的性能,再比如对于链表中的一个结点我们是无法直接…...

【Redis】高频面试题
提供五种常见的数据类型:String(字符串),Hash(哈希),List(列表),Set(集合)、Zset(有序集合) 文章目录 1、为什…...

数据分析基础
数据分析基础 1. 数据加载 使用 Pandas 库可以轻松地加载各种格式的数据,如 CSV、Excel、JSON 等。 import pandas as pd# 从 CSV 文件加载数据 data pd.read_csv(‘data.csv’). 2. 数据探索 一旦数据加载完成,我们可以开始对数据进行探索性分析&a…...

ffmpeg把一个平面视频,做成左右平面视频
要使用FFmpeg将单个平面视频转换为左右(或称为并排)3D格式的视频,你可以使用FFmpeg的filter_complex功能来实现。这种类型的视频通常用于3D视觉效果,其中同一画面的两个版本并排放置,每个版本略有不同的视角࿰…...
Docker搭建LNMP环境实战(02):Win10下安装VMware
实战开始,先安装 VMware 虚拟机。话不多说,上手就干! 1、基本环境检查 1.1、本机Bios是否支持虚拟化 进入:任务管理器- 性能,查看“虚拟化”是否启用,如果已启用,则满足要求,如果未…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
