【No.19】蓝桥杯简单数论上|模运算|快速幂|GCD|LCM|刷题统计|RSA解密|核桃的数量(C++)
简单数论
模运算
- 定义:模运算为 a 除以 m 的余数,记为 a mod m,有 a mod m = a % m
- 模运算是大数运算中的常用操作。
- 如果一个数太大,无法直接输出,或者不需要直接输出,可以把它取模后,缩小数值再输出。
- Python 虽然能直接计算大数,不用担心数据溢出,但是大数乘法太耗时,所以也常用取模来缩小数值。
- 一个简单应用,判断奇偶:
a%2==0,a 是偶数;a%2==1,a 是奇数
例题:刷题统计 2022 年第十三届省赛,lanqiaoOJ 题号 2098
【问题描述】
小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天做 a 道题目,周六和周日每天做 b 道题目。请你帮小明计算,按照计划他将在第几天实现做题数大于等于 n 题?
【输入格式】
输入一行包含三个整数 a, b 和 n。
【输出格式】
输出一个整数代表天数。
【评测用例规模与约定】
对于 50%的评测用例,1 ≤ a, b, n ≤ 10^6;
对于 100%的评测用例,1 ≤ a, b, n ≤ 10^18。
题目解析
求余数的简单题,利用求余,把计算复杂度降为 O(1)。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{ll a,b,n; cin >> a >> b >> n; //先输入a,b,nll week = a * 5+b * 2; //每周做题ll days = (n / week) * 7; //目前的天数n %= week; //剩下的做题数if(n <= a * 5) //在周一到周五内days += n / a + (n % a ? 1 : 0); //n/a计算整天数,还剩余的话+1else{ //周六和周日//不是在前五天,先把这5天加上,总刷题数再减去这5天做的days += 5, n -= a * 5;//再判断n/b,现在n只能是0~2b-1,判断需不需要多加1天days += n / b + (n % b ? 1 : 0);}cout << days;return 0;
}
快速幂
幂运算 a n a^n an,当 n 很大时,如果一个个乘,时间是 O(n) 的,速度很慢,此时可以用快速幂,在 O(logn) 的时间内算出来。
快速幂的一个解法:分治法,算 a 2 a^2 a2,然后再算 ( a 2 ) 2 (a^2)^2 (a2)2 ,…,一直算到 a n a^n an,代码也容易写。
- 标准的快速幂:用位运算实现。
- 基于位运算的快速幂,原理是倍增。
快速幂原理
以 a 11 a^{11} a11 为例说明如何用倍增法做快速幂。
(1)幂次与二进制的关系。把 a 11 a^{11} a11 分解成幂 a 8 a^{8} a8、 a 2 a^{2} a2、 a 1 a^{1} a1 的乘积: a 11 = a 8 + 2 + 1 = a 8 ∗ a 2 ∗ a 1 a^{11}=a^{8+2+1}=a^{8}*a^{2}*a^{1} a11=a8+2+1=a8∗a2∗a1。其中 a 1 a^{1} a1、 a 2 a^{2} a2、 a 4 a^{4} a4、 a 8 a^{8} a8…的幂次都是 2 的倍数,所有的幂 a i a^{i} ai 都是倍乘关系,逐级递推,代码: a *= a
(2)幂次用二进制分解。如何把 11 分解为 8+2+1?利用数的二进制的特征,n = 1 1 10 11_{10} 1110 = 101 1 2 1011_{2} 10112 = 2 3 + 2 1 + 2 0 = 8 + 2 + 1 2^3+2^1+2^0=8+2+1 23+21+20=8+2+1 ,把 n 按二进制处理就可以。
(3)如何跳过那些没有的幂次?例如 1011 需要跳过 a 4 a^4 a4。做个判断,用二进制的位运算实现:
- n & 1 :取 n 的最后一位,并且判断这一位是否需要跳过。
- n >>= 1 :把 n 右移一位,目的是把刚处理过的 n 的最后一位去掉。
幂运算的结果往往很大,一般会先取模再输出。 根据取模的性质有:
a^n mod m = (a mod m)^n mod m
所以可以边做幂边取模
例题:快速幂 lanqiaoOJ 题号 1514
【题目描述】
给定 b, p, k,求(b^p) mod k。
其中 2≤b, p, k≤10^9。
【输入描述】
三个整数 b,p,k。
【输出描述】
输出(b^p) mod k。
题目解析
#include <bits/stdc++.h>
using namespace std;
typedef long long ll; //变量改用较大的long long
ll fastPow(ll a, ll n, ll mod)
{ll ans = 1;a %= mod; //重要,防止下面的ans*a越界while(n) {if(n & 1) //取第一位,如果是1的话ans = (ans*a) % mod; //取模,纳入到ans里面去a = a*a % mod; //取模,a倍增n >>= 1; //把这位去掉}return ans;
}
int main(){ll b, p, k; cin >> b >> p >> k;cout << fastPow(b,p,k);return 0;
}
RSA解密
【题目描述】
RSA 是一种经典的加密算法。它的基本加密过程如下
首先生成两个质数 p、q,令n=p·q,设d与(p-1)·(q-1)互质,则可找到e使得d·e 除(p-1)(q-1)的余数为1。
n、d、e 组成了私钥,n、d 组成了公钥。
当使用公钥加密一个整数X 时(小于n),计算c= X d X^d Xd mod n,则C是加密后的密文。
当收到密文C时,可使用私钥解开,计算公式为X= C e C^e Ce modn。
例如,当p=5,q=11,d=3时,n=55,e=27.
若加密数字24,得 2 4 3 24^3 243 mod 55 = 19。解密数字19,得 1 9 27 19^{27} 1927 mod 55 = 24。
现在你知道公钥中n=1001733993063167141,d=212353,同时你截获了别人发送的密文C=20190324,请问,原文是多少?
题目解析
(1)求p、q (两个质数 p、q,n=p·q)
先求n的素因子p和q。由于n只有p、q这2个因子,没有别的因子,所以p和q必然有一个小于 n \sqrt{ n } n,找到一个,另一个就知道了。
用暴力法求p、q,用i循环从2到 n \sqrt{ n } n一个个试。
若n除以i的余数是0,i就是因子。
循环次数是 n = 1001733993063167141 n=\sqrt{1001733993063167141 } n=1001733993063167141,
1000866621即十亿次计算。得到:p=891234941、q=1123984201
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
int main()
{ll n = 1001733993063167141;ll k = sqrt(n);for (ll i = 2; i <= k; i ++){if (n % i == 0)cout << i << " " << n/i;}return 0;
}
(2)求e (找到e 使得d·e 除(p-1)·(q-1)的余数为1
用到大数了。c++的64位long long不够用,虽然有 int128类型,但是有些编译器不支持。
还是用Python,下面代码打印出e=823816093931522017。
注意e有很多个,取最小的一个就行了。
#include <bits/stdc++.h>
using namespace std;
typedef __int128 ll;
void print(__int128 num)
{//递归调用,实现从高位向低位输出if(num>9)print(num / 10);putchar(num % 10 + '0');
int main()
{ll n= 1001733993063167141;ll d = 212353;ll p = 891234941;ll q = 1123984201;ll tmp = (p - 1)*(q - 1);print(tmp);puts("");for(ll i = 2; i <= n; i ++){ll now = i * tmp + 1;if(now % d == 0){ll t = now / d;print(t); //有很多e,求第一个就行了break;}}return 0;
}
(3)求X= C e C^e Ce mod n
#include <bits/stdc++.h>
using namespace std;
typedef __int128 ll;
void print( int128 num)
{//递归调用,实现从高位向低位输出if(num > 9)print(num / 10);putchar(num % 10 + '0');
}
ll fastPow(ll a, ll b, ll mod)
{ll ans = 1;while(b){if(b & 1)ans = ans * a % mod;a = a * a % mod;b >>= 1;}return ans;
}
int main()
{ll n = 1001733993063167141;ll e = 823816093931522017;ll C = 20190324;print(fastPow(C,e,n));//打印结果:579706994112328949return 0;
}
GCD 定义、性质
最大公约数 Greatest Common Divisor(GCD):
整数 a 和 b 的 GCD 是指能同时整除 a 和 b 的最大整数,记为 gcd(a, b)。由于-a 的因子和 a 的因子相同,因此 gcd(a, b) = gcd(|a|, |b|)。
编码时只关注正整数的最大公约数。
性质:
- gcd(a, b) = gcd(a, a+b) = gcd(a, k·a+b)
- gcd(ka, kb) = k·gcd(a, b)
- 定义多个整数的最大公约数:gcd(a, b, c) = gcd(gcd(a, b), c)。
- 若 gcd(a, b) = d,则 gcd(a/d, b/d) = 1,即 a/d 与 b/d 互素
- gcd(a+cb, b) = gcd(a, b)
c++函数 std::__gcd(),可以返回负数,可以带多个参数。
#include <bits/stdc++.h>
using namespace std;
int main()
{cout << __gcd(15, 81) << "\n"; // 输出 3cout << __gcd(0, 44) << "\n"; // 输出 44cout << __gcd(0, 0) << "\n"; // 输出 0cout << __gcd(-6, -15) << "\n"; // 输出 -3cout << __gcd(-17,289) << "\n"; // 输出 -17cout << __gcd(17,-289) <<"\n"; // 输出 17return 0;
}
手写 GCD 代码
手写 gcd 函数,常用欧几里得算法。
辗转相除法求 gcd:
gcd(a, b) = gcd(b, a mod b)
这是最常用的方法,极为高效。
设 a > b,辗转相除法的计算复杂度为 O ( ( log 2 a ) 3 ) O((\log_{2}a)^3) O((log2a)3)。
可输出负数,和库函数一样:
#include<bits/stdc++.h>
using namespace std;
int gcd(int a, int b)
{ return b ? gcd(b, a % b) : a;
}
int main()
{cout << gcd(15, 81) << "\n"; // 输出 3cout << gcd(0, 44) << "\n"; // 输出 44cout << gcd(0, 0) << "\n"; // 输出 0cout << gcd(-6, -15) << "\n"; // 输出 -3cout << gcd(-17,289) << "\n"; // 输出 -17cout << gcd(17,-289) << "\n"; // 输出 17return 0;
}
// 或者使用如下编码方式:
// int GCD(int a,int b)
// {
// if(b==0)
// return a;
// return GCD(b,a%b);
// }
LCM
最小公倍数 LCM (the Least Common Multiple) 。
a 和 b 的最小公倍数 lcm(a,b),从算术基本定理推理得到。
算术基本定理:任何大于 1 的正整数 n 都可以唯一分解为有限个素数的乘积:
n = p 1 c 1 p 2 c 2 p 3 c 3 … p m c m n=p_{1}^{c_{1}}p_{2}^{c_{2}}p_{3}^{c_{3}}\dots p_{m}^{c_{m}} n=p1c1p2c2p3c3…pmcm,其中 c i c_{i} ci 都是正整数, p i p_{i} pi 都是素数且从小到大。
推导 LCM:
设: a = p 1 c 1 p 2 c 2 p 3 c 3 … p m c m a=p_{1}^{c_{1}}p_{2}^{c_{2}}p_{3}^{c_{3}}\dots p_{m}^{c_{m}} a=p1c1p2c2p3c3…pmcm, b = p 1 f 1 p 2 f 2 p 3 f 3 … p m f m b=p_{1}^{f_{1}}p_{2}^{f_{2}}p_{3}^{f_{3}}\dots p_{m}^{f_{m}} b=p1f1p2f2p3f3…pmfm
那么: g c d ( a , b ) = p 1 m i n ( c 1 , f 1 ) p 2 m i n ( c 2 , f 2 ) p 3 m i n ( c 3 , f 3 ) … p m m i n ( c m , f m ) gcd(a,b)=p_{1}^{min(c_{1},f_{1})}p_{2}^{min(c_{2},f_{2})}p_{3}^{min(c_{3},f_{3})}\dots p_{m}^{min(c_{m},f_{m})} gcd(a,b)=p1min(c1,f1)p2min(c2,f2)p3min(c3,f3)…pmmin(cm,fm)
l c m ( a , b ) = p 1 m a x ( c 1 , f 1 ) p 2 m a x ( c 2 , f 2 ) p 3 m a x ( c 3 , f 3 ) … p m m a x ( c m , f m ) lcm(a,b)=p_{1}^{max(c_{1},f_{1})}p_{2}^{max(c_{2},f_{2})}p_{3}^{max(c_{3},f_{3})}\dots p_{m}^{max(c_{m},f_{m})} lcm(a,b)=p1max(c1,f1)p2max(c2,f2)p3max(c3,f3)…pmmax(cm,fm)
推出: g c d ( a , b ) ∗ l c m ( a , b ) = a ∗ b gcd(a,b)*lcm(a,b) = a*b gcd(a,b)∗lcm(a,b)=a∗b
即:
l c m ( a , b ) = a ∗ b / g c d ( a , b ) = a / g c d ( a , b ) ∗ b lcm(a,b)=a∗b/gcd(a,b)=a/gcd(a,b)∗b lcm(a,b)=a∗b/gcd(a,b)=a/gcd(a,b)∗b
lcm()手写代码
//c or c++
int lcm(int a, int b)
{ //需要的时候把int改成long longreturn a / gcd(a, b) * b; //先做除法再做乘法,防止先做乘法溢出
}
核桃的数量 2013 年第四届省赛 lanqiaoOJ 题号 210
【题目描述】
小张是软件项目经理,他带领 3 个开发组。工期紧,今天都在加班呢。为鼓舞士气,小张打算给每个组发一袋核桃(据传言能补脑)。他的要求是:
- 各组的核桃数量必须相同
- 各组内必须能平分核桃(当然是不能打碎的)
- 尽量提供满足 1, 2 条件的最小数量(节约闹革命嘛)
【输入格式】
输入三个正整数 a, b, c,表示每个组正在加班的人数,用空格分开
(a,b,c< 30)
【输出格式】
输出一个正整数,表示每袋核桃的数量。
题目解析
简单题,答案就是三个数字的最小公倍数。
#include <bits/stdc++.h>
using namespace std;
int lcm(int a, int b)
{ return a / __gcd(a, b) * b;
}
int main()
{int a, b, c; cin >> a >> b >> c;int k = lcm(a,b);cout << lcm(k,c) << endl;return 0;
}
相关文章:
)
【No.19】蓝桥杯简单数论上|模运算|快速幂|GCD|LCM|刷题统计|RSA解密|核桃的数量(C++)
简单数论 模运算 定义:模运算为 a 除以 m 的余数,记为 a mod m,有 a mod m a % m模运算是大数运算中的常用操作。如果一个数太大,无法直接输出,或者不需要直接输出,可以把它取模后,缩小数值再…...

区块链安全之DDoS防护的重要性及其实施策略
随着区块链技术的不断发展和广泛应用,其安全问题也日益凸显。其中,分布式拒绝服务(DDoS)攻击是对区块链网络稳定性和效率构成潜在威胁的重要因素之一。本文旨在深入探讨区块链为何需要采取DDoS高防措施,并提出相应的防护策略。 一、区块链面…...
使用Spark单机版环境
在Spark单机版环境中,可通过多种方式进行实战操作。首先,可使用特定算法或数学软件计算圆周率π,并通过SparkPi工具验证结果。其次,在交互式Scala版或Python版Spark Shell中,可以进行简单的计算、打印九九表等操作&…...
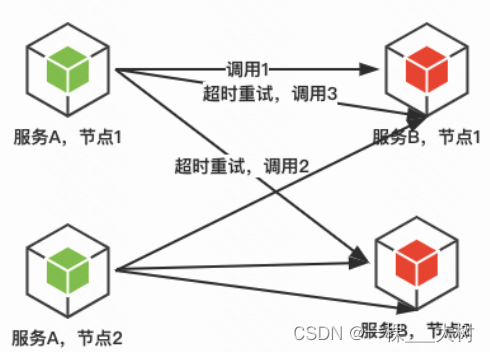
【分布式】——降级熔断限流
降级&熔断&限流 ⭐⭐⭐⭐⭐⭐ Github主页👉https://github.com/A-BigTree 笔记仓库👉https://github.com/A-BigTree/tree-learning-notes 个人主页👉https://www.abigtree.top ⭐⭐⭐⭐⭐⭐ 如果可以,麻烦各位看官顺手点…...
代码随想录刷题笔记 Day 58 | 判断子序列 No.392 | 不同的子序列 No.115
文章目录 Day 5801. 判断子序列(No. 392)<1> 题目<2> 题解<3> 代码 02. 不同的子序列(No. 115)<1> 题目<2> 题解<3> 代码 Day 58 01. 判断子序列(No. 392) 题目链接…...
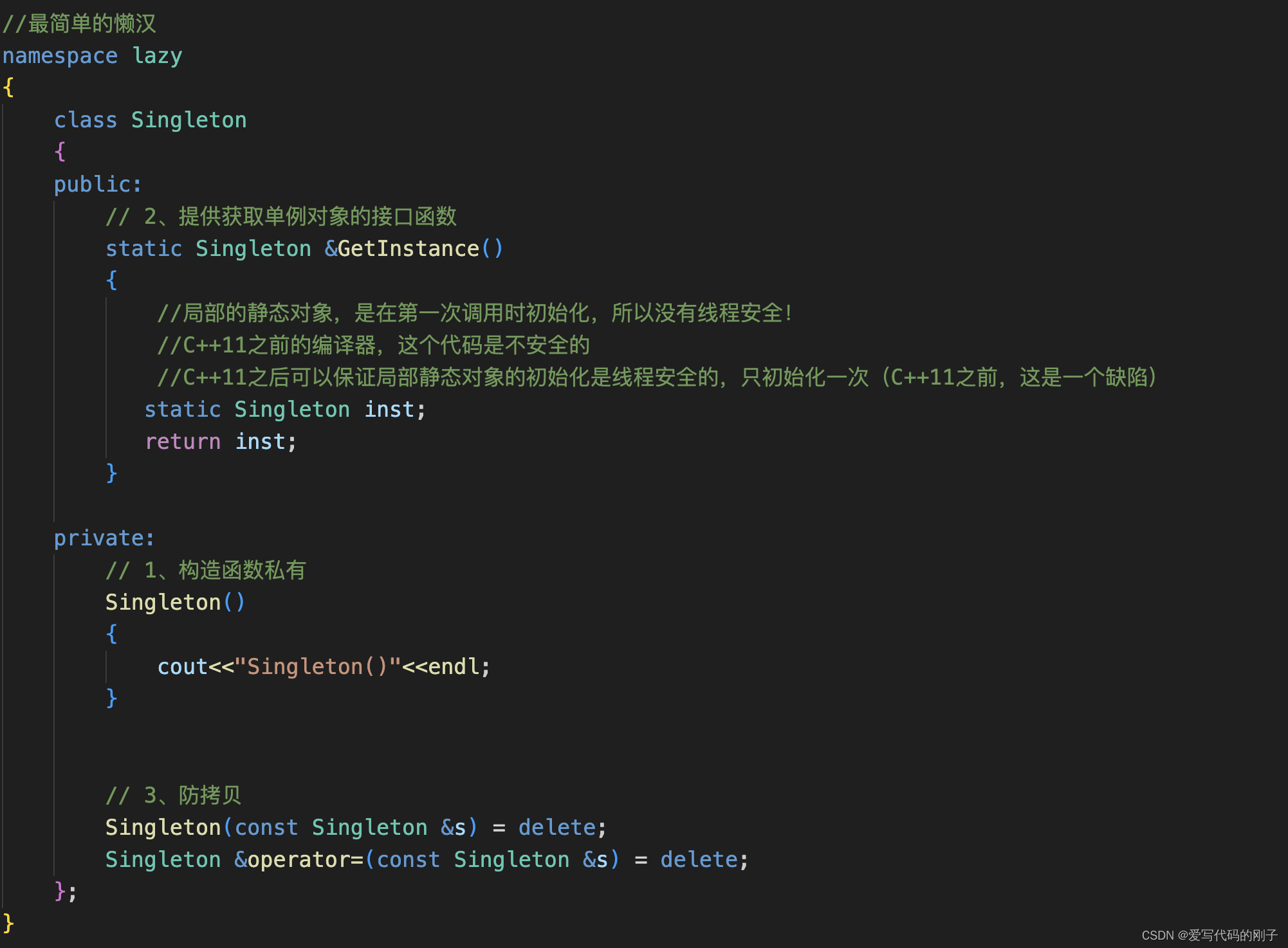
【C++11】thread线程库
【C11】thread线程库 目录 【C11】thread线程库thread类的简单介绍函数指针lambda表达式常用在线程中 线程函数参数join与detach利用RAII思想来自动回收线程 原子性操作库(atomic)atomic中的load函数:atomic中对变量进行原子操作的一些函数 CAS(Compare-And-Swap)无…...
实例镜像及实例创建方法)
【OpenStack】创建系统(VM)实例镜像及实例创建方法
【OpenStack】创建系统(VM)实例镜像及实例创建方法 目录 【OpenStack】创建系统(VM)实例镜像及实例创建方法创建计算镜像加载基本镜像预建镜像手动实例创建cloud-init 搭救使用 `cloud-init` 配置启动实例连接到您的新实例为实例分配 Floating IP创建SSH隧道结论推荐超级课程:…...

灵途科技助力家电智能创新
从智能家电到个护健康,科技无时无刻不在刷新我们对智慧生活的认知,我们也从未像今天这样近距离贴近智慧生活的朴素本质——传感技术。灵途科技专注光电感知技术,持续为智能家电客户提供成熟的全方位感知解决方案。步入发展第八年,…...
Flask python :logging日志功能使用
logging日志的使用 一、了解flask日志1.1、Loggers记录器1.2、Handlers 处理器1.3、Formatters 格式化器 二、使用日志2.1、官网上的一个简单的示例2.2、基本配置2.3、具体使用示例2.4、运行 三、写在最后 一、了解flask日志 日志是一种非常重要的工具,可以帮助开发…...

ethers.js:sign(签名)
Signers 在ethers中Signer是以太坊账户的抽象,可以用来签名消息和交易,如将签名的交易发送到以太坊网络以执行状态更改的操作。 npm install ethers5.4.0// 引入 import { ethers } from ethers签名 this.provider new ethers.providers.Web3Provider(…...

使用npm i进行admin依赖安装的时候出现问题
提示: npm ERR! code CERT_HAS_EXPIRED npm ERR! errno CERT_HAS_EXPIRED npm ERR! request to https://registry.npm.taobao.org/string-width failed, reason: certificate has expired 切换淘宝源到http或者更换其他国内镜像 npm config set registry http:/…...
)
【Python笔记-FastAPI】定时任务实现(APScheduler)
目录 一、常见触发器 (一) DateTrigger (二) IntervalTrigger (三) CronTrigger (四) CombinationTrigger 二、代码示例 (一) task_scheduler.py (二) client.py 三、调用说明 (一) 注册任务 (二) 查询任务 (三) 删除任务 实现功能: 定时任务注册、修改、删除、查…...

『Apisix入门篇』从零到一掌握Apache APISIX:架构解析与实战指南
📣读完这篇文章里你能收获到: 🌐 深入Apache APISIX架构: 从Nginx到OpenResty,再到etcd,一站式掌握云原生API网关的构建精髓,领略其层次化设计的魅力。 🔌 核心组件全解析ÿ…...

easyExcel大数据量导出oom
easyExcel大数据量导出 异常信息 com.alibaba.excel.exception.ExcelGenerateException: java.lang.OutOfMemoryError: GC overhead limit exceededat com.alibaba.excel.write.ExcelBuilderImpl.fill(ExcelBuilderImpl.java:84)at com.alibaba.excel.ExcelWriter.fill(Excel…...

react native上传二进制图片、视频的方法
react native获取本地图片我用的react-native-image-picker,但是它只能获取图片路径,以及base64的图片,不能获取到binary二进制形式的。 一开始我是让后端改造接口,把原本传binary的改成了base64,可是,躲得…...
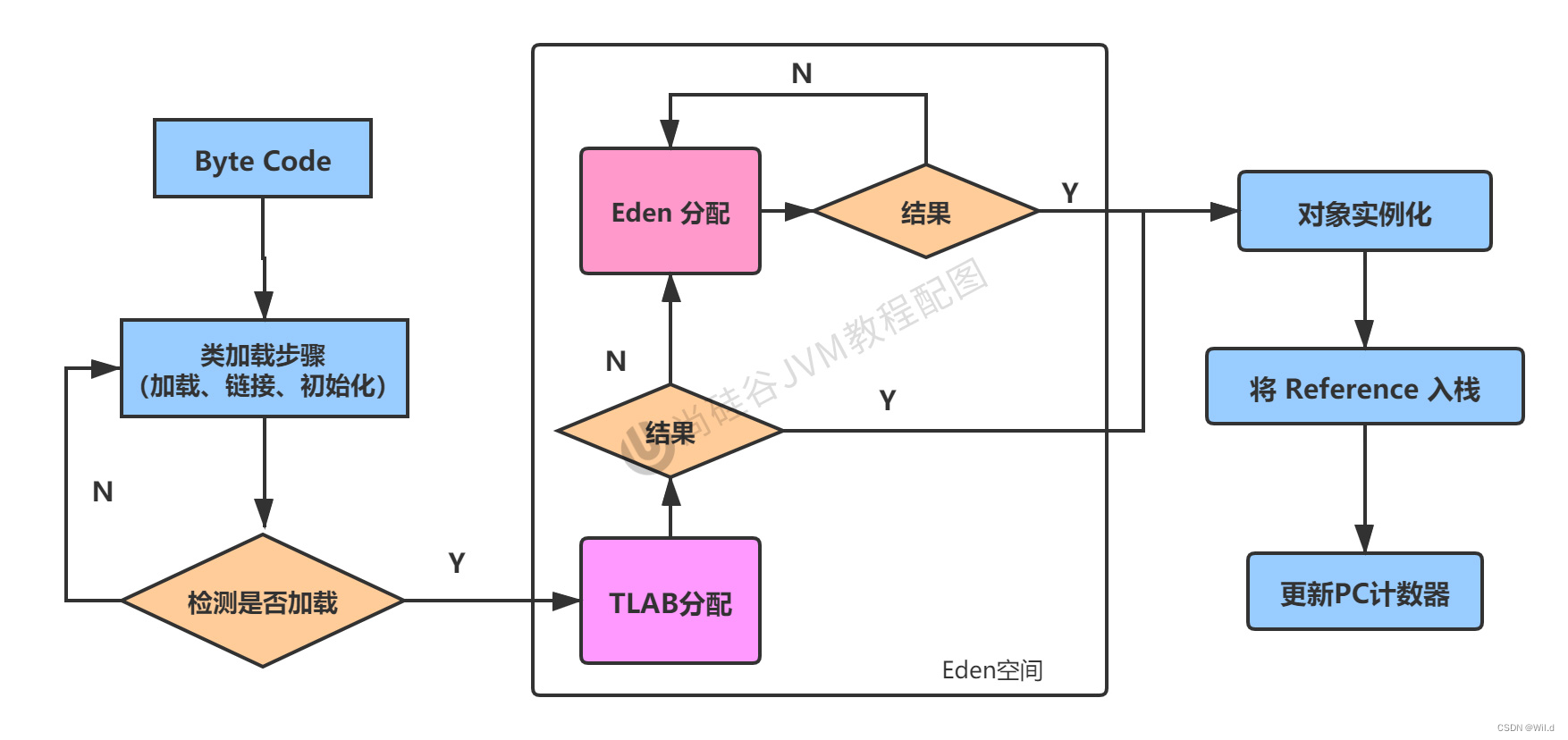
JVM之堆
堆的核心概述 一个JVM实例只存在一个堆内存,堆也是内存管理的核心区域。 Java堆区在JVM启动的时候即被创建,其空间大小也就确定了。是JVM管理的最大一块内存空间。 堆内存的大小是可以调节的。 《JVM虚拟机规范》规定,堆可以处于物理上不连…...
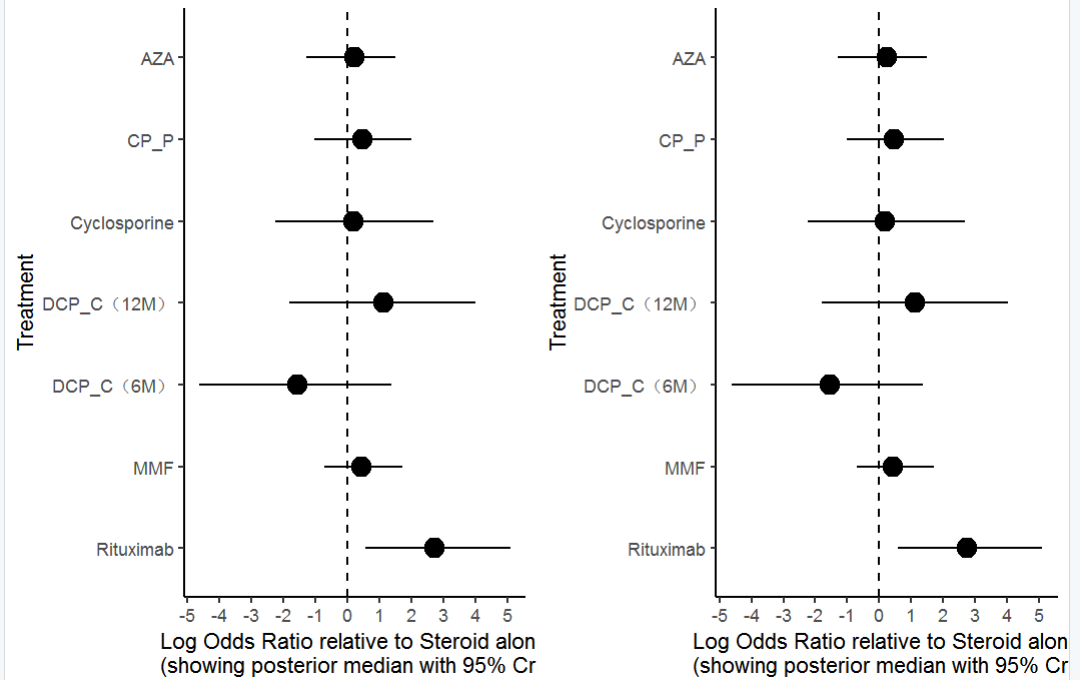
R语言实现——网状 Meta 分析
近来年,网状 Meta 分析相关研究不断涌现,此类研究不但能发表在国内各大核心期刊上,还能在SCI期刊甚至医学4大刊上看到其身影。随手在pubmed上面一搜索,就能得到一万多篇相关文献。俨然成为医学文献研究的“大杀器”! P…...
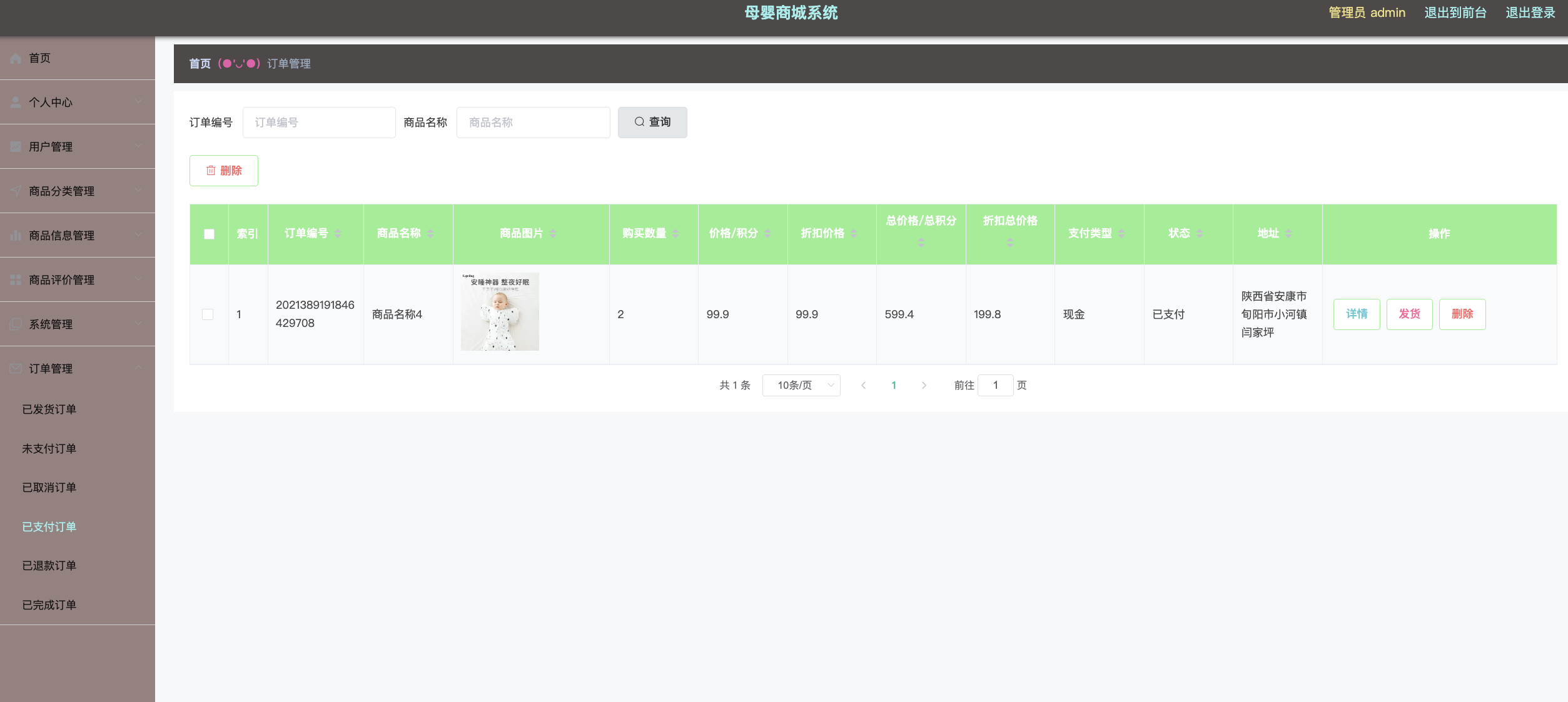
Java项目:77 springboot母婴商城
作者主页:源码空间codegym 简介:Java领域优质创作者、Java项目、学习资料、技术互助 文中获取源码 项目介绍 本课题后端使用SpringBoot Spring Cloud框架,前端采用html,JQuery,JS,DIVCSS技术进行编程&…...

【排序算法】深入解析快速排序(霍尔法三指针法挖坑法优化随机选key中位数法小区间法非递归版本)
文章目录 📝快速排序🌠霍尔法🌉三指针法🌠挖坑法✏️优化快速排序 🌠随机选key🌉三位数取中 🌠小区间选择走插入,可以减少90%左右的递归🌉 快速排序改非递归版本…...

生成微信小程序二维码
首页 -> 统计 可以通过上面二个地方配置,生成小程序的二维码,并且在推广分析里,有详细的分析数据,...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
