【机器学习之---数学】马尔科夫链
every blog every motto: You can do more than you think.
https://blog.csdn.net/weixin_39190382?type=blog
0. 前言
马尔科夫

1. 概念
1.1 引言
马尔可夫链在许多领域都有应用,包括物理学、生物学、工程学、经济学和计算机科学等。在计算机科学中,特别是在算法设计、复杂性理论、网络科学和人工智能等领域,马尔可夫链是一个基本的概念。
马尔可夫链是随机过程 这门课程中的一部分。简单来说,随机过程就是使用统计模型一些事物的过程进行预测和处理 ,比如股价预测通过今天股票的涨跌,却预测明天后天股票的涨跌;天气预报通过今天是否下雨,预测明天后天是否下雨。这些过程都是可以通过数学公式进行量化计算的。通过下雨、股票涨跌的概率,用公式就可以推导出来 N 天后的状况。
它是一个离散时间随机过程,其中系统的下一个状态只依赖于当前状态,与过去的状态无关。这种“无后效性”(无记忆性)是马尔可夫链的核心特性(马尔科夫性)。
1.2 马尔可夫过程和马尔科夫链
其中,涉及两个概念,马尔科夫过程和马尔科夫链。
马尔科夫过程:
- 是一个随机过程,其特点是系统未来的状态仅依赖于当前状态,与过去的状态无关。
- 它可以在任何时间点定义,并可以在连续或离散的时间框架下进行。
- 马尔科夫过程可以是连续状态的,也可以是离散状态的。
马尔科夫链:
- 是一种特殊的马尔科夫过程,它通常描述的是离散时间序列上的状态转移。
- 它由一系列离散状态组成,每个状态之间的转移遵循马尔科夫性质,即仅依赖于当前状态。
- 马尔科夫链通常用转移概率矩阵来描述,这些概率表示在当前时间步从一个状态转移到另一个状态的概率。
简而言之,所有马尔科夫链都是马尔科夫过程,但不是所有马尔科夫过程都是马尔科夫链。 马尔科夫链是马尔科夫过程在离散时间框架下的一个具体实现。在实际应用中,特别是在计算机科学和工程学中,马尔科夫链的概念更为常见,因为它易于建模和分析。而马尔科夫过程的概念更加广泛,包括连续时间马尔科夫过程和更复杂的结构。
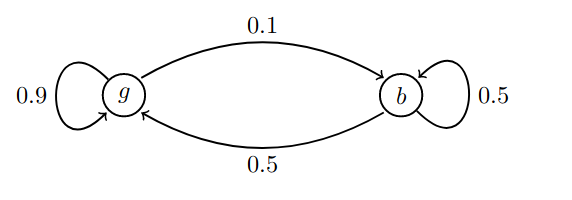
1.3 数学定义
有序列状态: . . . X t − 2 , X t − 1 , X t , X t − 1 , . . . ...X_{t-2},X_{t-1},X_t,X_{t-1},... ...Xt−2,Xt−1,Xt,Xt−1,...,那么 X t − 1 X_{t-1} Xt−1时刻的状态,只与 X t − 1 X_{t-1} Xt−1时刻的状态有关,与 X t − 2 X_{t-2} Xt−2时刻的状态无关。
P ( X t + 1 ∣ . . . X t − 2 , X t − 1 , X t , . . . ) = P ( X t + 1 ∣ X t ) P(X_{t+1}|...X_{t-2},X_{t-1},X_t,...) = P(X_{t+1}|X_t) P(Xt+1∣...Xt−2,Xt−1,Xt,...)=P(Xt+1∣Xt)
既然某一时刻状态转移的概率只依赖于它的前一个状态 ,那么我们只要能求出系统中任意两个状态之间的转换概率,这个马尔科夫链的模型就定了。
通过马尔科夫链的模型转换,我们可以将事件的状态转换成概率矩阵 (又称状态分布矩阵 ),如下例:
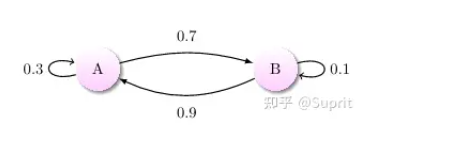
其转移概率矩阵为:

有了状态转移矩阵以后,我们就可以很方便的计算n步以后在A和B的概率了。
1.4 性质
1.4.1 稳态分布
状态转移矩阵有一个非常重要的特性,经过一定有限次数序列的转换,最终一定可以得到一个稳定的概率分布 ,且与初始状态概率分布无关。
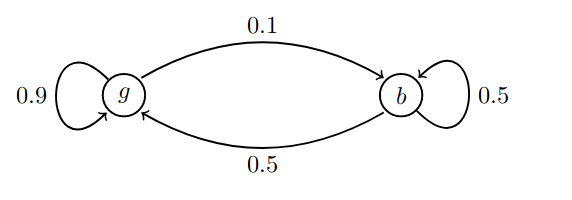
若,计算n天以后再g点的概率,则有:
$$
P_g{X_n = g} = (P^n)_{gg} \
P_b{ X_n=g } = (P^n)_{bg} \
$$
下表是n天以后在g点的概率:
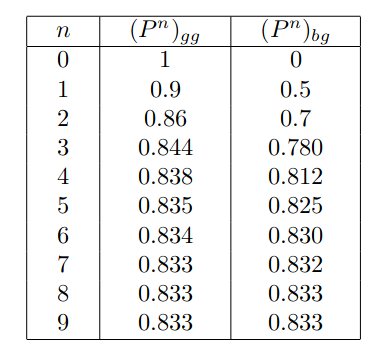
我们发现马尔科夫链会“忘记”初始状态(无记忆性), 最终会收敛到稳定概率分布。
2. 应用
自然语音处理研究让机器“听懂”人类的语言,马尔科夫模型就解决了:
语言模型:N-Gram 是一种简单有效的语言模型,基于独立输入假设:第 n 个词的出现只与前面 N-1 个词相关,而与其它任何词都不相关 。整句出现的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计 N 个词同时出现的次数得到。

参考
- https://zhuanlan.zhihu.com/p/448575579
- https://zhuanlan.zhihu.com/p/489239366
- https://blog.csdn.net/qq_27825451/article/details/100117715#t0
相关文章:

【机器学习之---数学】马尔科夫链
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 马尔科夫 1. 概念 1.1 引言 马尔可夫链在许多领域都有应用,包括物理学、生物学、工程学、经济学和计算机科学等。在计算机科学中࿰…...

教程3_图像的轮廓
目录 目标 1. 特征矩 2、轮廓质心 3. 轮廓面积 4. 轮廓周长 5. 轮廓近似 6. 轮廓凸包 7. 边界矩形 7.1.直角矩形 7.2. 旋转矩形 8. 最小闭合圈 9. 拟合一个椭圆 10. 拟合直线 目标 在本文中,我们将学习 - 如何找到轮廓的不同特征,例如面积&…...
【Linux】-Linux下的编辑器Vim的模式命令大全及其自主配置方法
目录 1.简单了解vim 2.vim的模式 2.1命令模式 2.2插入模式 2.3底行模式 3.vim各模式下的命令集 3.1正常(命令模式下) 3.1.1光标定位命令 3.1.2 复制粘贴 3.1.3 删除 3.1.4 撤销 3.1.5大小写转换 3.1.6替换 「R」:替换光标所到之处的字符&…...
基于SpringBoot和Vue的车辆管理系统的设计与实现
今天要和大家聊的是一款基于SpringBoot和Vue的车辆管理系统的设计与实现 !!! 有需要的小伙伴可以通过文章末尾名片咨询我哦!!! 💕💕作者:李同学 💕…...
R折线图(自备)
目录 折线图基础 创建散点和折线图 复杂折现加图例 折线图柱状图 数据处理 进行差异检验 基础绘图折线 基础绘图箱线 进行合并 双轴柱状与折线图 数据 折线图基础 创建散点和折线图 rm(list ls()) opar <-par(no.readonlyTRUE)##自带orange数据集 par(mfrowc…...
web学习笔记(四十五)Node.js
目录 1. Node.js 1.1 什么是Node.js 1.2 为什么要学node.js 1.3 node.js的使用场景 1.4 Node.js 环境的安装 1.5 如何查看自己安装的node.js的版本 1.6 常用终端命令 2. fs 文件系统模块 2.1引入fs核心模块 2.2 读取指定文件的内容 2.3 向文件写入指定内容 2.4 创…...
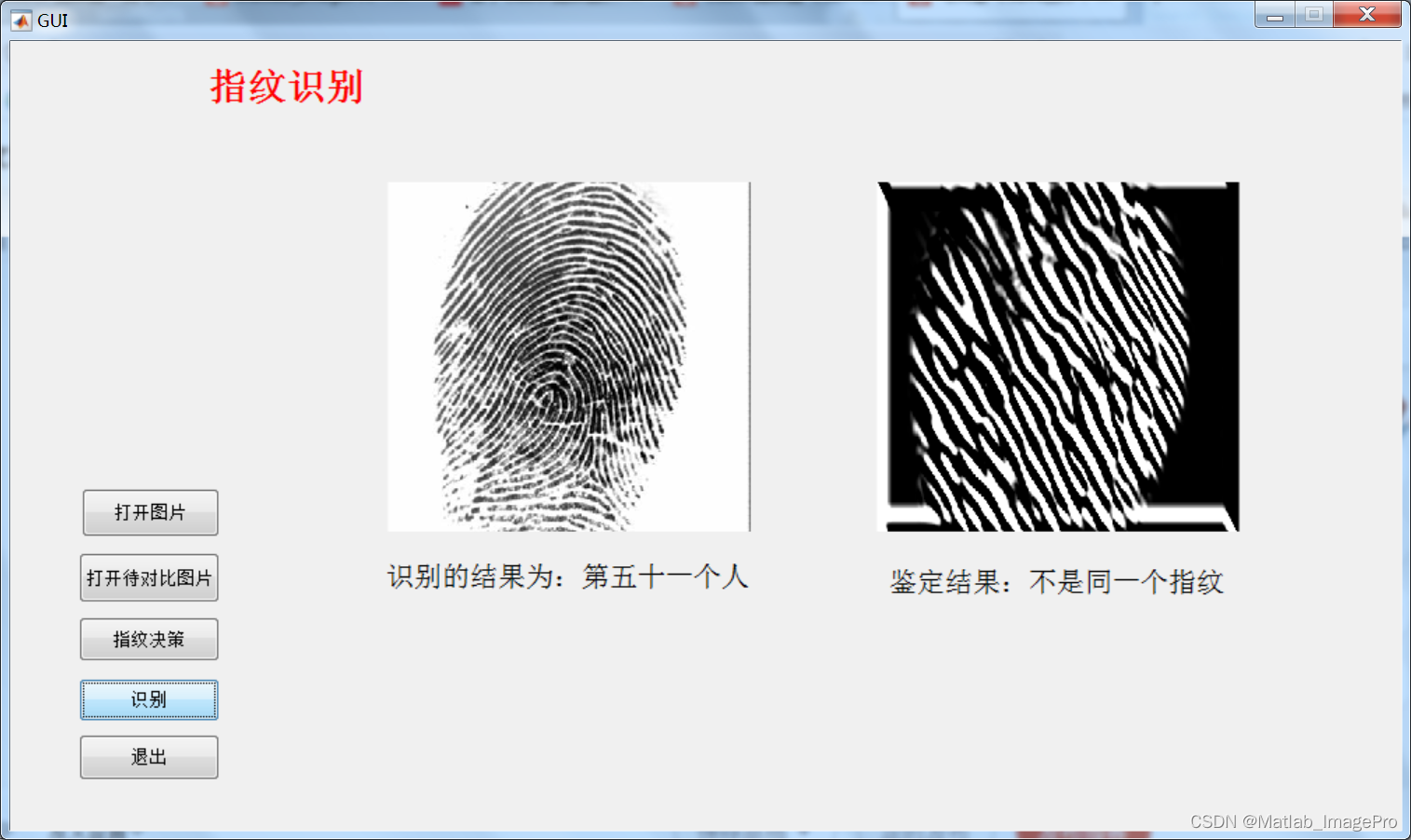
基于Gabor滤波器的指纹图像识别,Matlab实现
博主简介: 专注、专一于Matlab图像处理学习、交流,matlab图像代码代做/项目合作可以联系(QQ:3249726188) 个人主页:Matlab_ImagePro-CSDN博客 原则:代码均由本人编写完成,非中介,提供…...

55、Qt/事件机制相关学习20240326
一、代码实现设置闹钟,到时间后语音提醒用户。示意图如下: 代码: #include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget), speecher(new QTextToSpeech(t…...

Clip Converter - 视频在线下载方法
Clip Converter - 视频在线下载方法 1. Video URL to Download2. Continue3. StartReferences YT to MP4 & MP3 Converter! https://www.clipconverter.cc/ Clip Converter is a free online media conversion application, which allows you to reocord, convert and do…...
)
【No.19】蓝桥杯简单数论上|模运算|快速幂|GCD|LCM|刷题统计|RSA解密|核桃的数量(C++)
简单数论 模运算 定义:模运算为 a 除以 m 的余数,记为 a mod m,有 a mod m a % m模运算是大数运算中的常用操作。如果一个数太大,无法直接输出,或者不需要直接输出,可以把它取模后,缩小数值再…...

区块链安全之DDoS防护的重要性及其实施策略
随着区块链技术的不断发展和广泛应用,其安全问题也日益凸显。其中,分布式拒绝服务(DDoS)攻击是对区块链网络稳定性和效率构成潜在威胁的重要因素之一。本文旨在深入探讨区块链为何需要采取DDoS高防措施,并提出相应的防护策略。 一、区块链面…...
使用Spark单机版环境
在Spark单机版环境中,可通过多种方式进行实战操作。首先,可使用特定算法或数学软件计算圆周率π,并通过SparkPi工具验证结果。其次,在交互式Scala版或Python版Spark Shell中,可以进行简单的计算、打印九九表等操作&…...
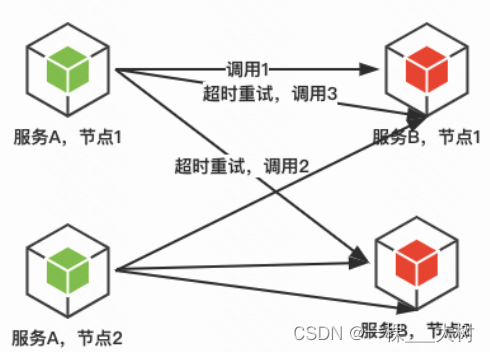
【分布式】——降级熔断限流
降级&熔断&限流 ⭐⭐⭐⭐⭐⭐ Github主页👉https://github.com/A-BigTree 笔记仓库👉https://github.com/A-BigTree/tree-learning-notes 个人主页👉https://www.abigtree.top ⭐⭐⭐⭐⭐⭐ 如果可以,麻烦各位看官顺手点…...
代码随想录刷题笔记 Day 58 | 判断子序列 No.392 | 不同的子序列 No.115
文章目录 Day 5801. 判断子序列(No. 392)<1> 题目<2> 题解<3> 代码 02. 不同的子序列(No. 115)<1> 题目<2> 题解<3> 代码 Day 58 01. 判断子序列(No. 392) 题目链接…...
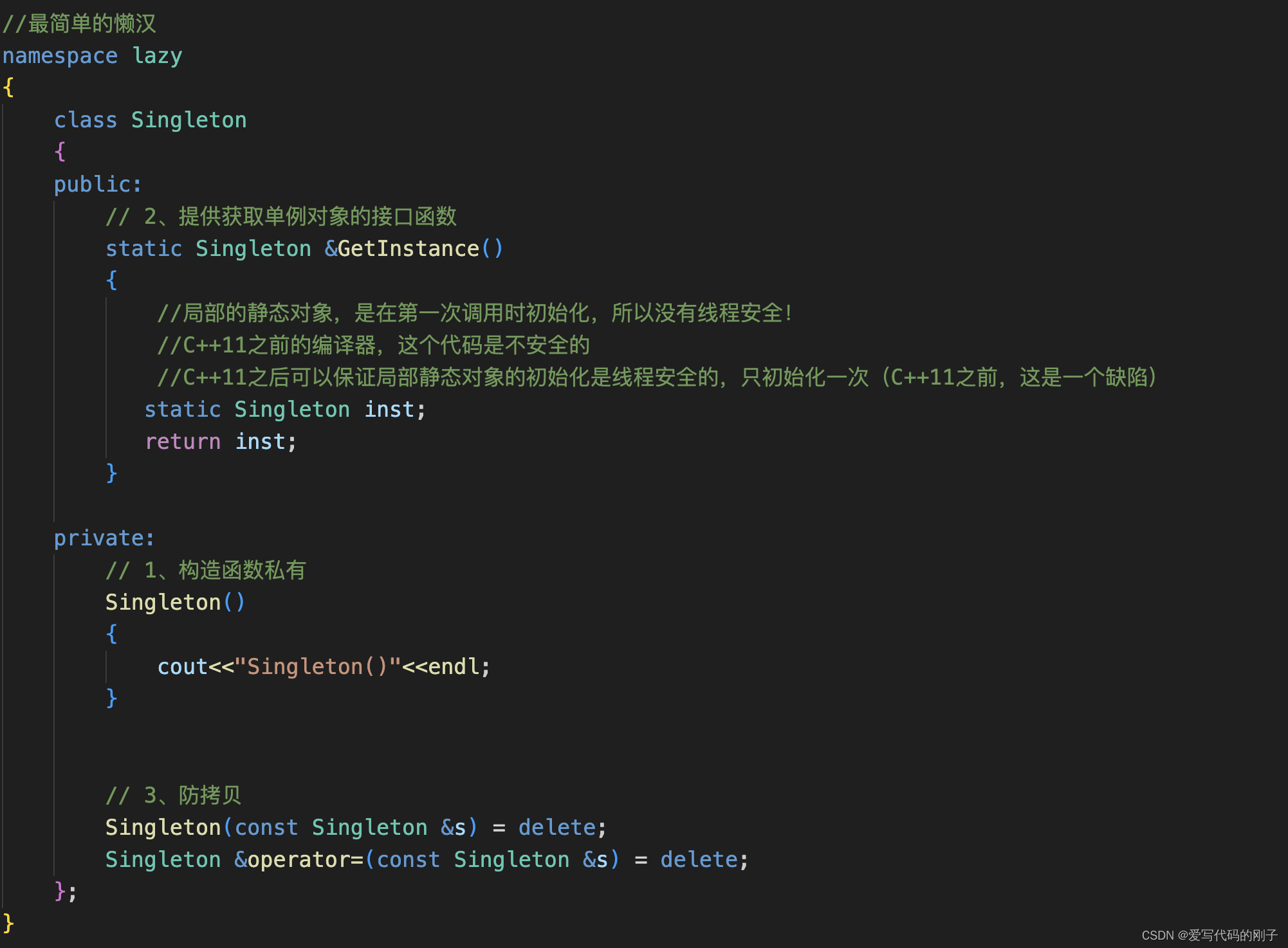
【C++11】thread线程库
【C11】thread线程库 目录 【C11】thread线程库thread类的简单介绍函数指针lambda表达式常用在线程中 线程函数参数join与detach利用RAII思想来自动回收线程 原子性操作库(atomic)atomic中的load函数:atomic中对变量进行原子操作的一些函数 CAS(Compare-And-Swap)无…...
实例镜像及实例创建方法)
【OpenStack】创建系统(VM)实例镜像及实例创建方法
【OpenStack】创建系统(VM)实例镜像及实例创建方法 目录 【OpenStack】创建系统(VM)实例镜像及实例创建方法创建计算镜像加载基本镜像预建镜像手动实例创建cloud-init 搭救使用 `cloud-init` 配置启动实例连接到您的新实例为实例分配 Floating IP创建SSH隧道结论推荐超级课程:…...

灵途科技助力家电智能创新
从智能家电到个护健康,科技无时无刻不在刷新我们对智慧生活的认知,我们也从未像今天这样近距离贴近智慧生活的朴素本质——传感技术。灵途科技专注光电感知技术,持续为智能家电客户提供成熟的全方位感知解决方案。步入发展第八年,…...
Flask python :logging日志功能使用
logging日志的使用 一、了解flask日志1.1、Loggers记录器1.2、Handlers 处理器1.3、Formatters 格式化器 二、使用日志2.1、官网上的一个简单的示例2.2、基本配置2.3、具体使用示例2.4、运行 三、写在最后 一、了解flask日志 日志是一种非常重要的工具,可以帮助开发…...

ethers.js:sign(签名)
Signers 在ethers中Signer是以太坊账户的抽象,可以用来签名消息和交易,如将签名的交易发送到以太坊网络以执行状态更改的操作。 npm install ethers5.4.0// 引入 import { ethers } from ethers签名 this.provider new ethers.providers.Web3Provider(…...

使用npm i进行admin依赖安装的时候出现问题
提示: npm ERR! code CERT_HAS_EXPIRED npm ERR! errno CERT_HAS_EXPIRED npm ERR! request to https://registry.npm.taobao.org/string-width failed, reason: certificate has expired 切换淘宝源到http或者更换其他国内镜像 npm config set registry http:/…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...
