【Python操作基础】——元组
🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972
个人介绍: 研一|统计学|干货分享
擅长Python、Matlab、R等主流编程软件
累计十余项国家级比赛奖项,参与研究经费10w、40w级横向
文章目录
- 1 定义方法
- 2 主要特征
- 3 基本用法
- 4 应用场景
【Python操作基础】系列——元组操作,建议收藏!
该篇文章首先利用Python展示了使用元组类型数据的相关操作,包括定义方法;主要特征;基本用法;应用场景等。
1 定义方法
运行程序:
myTuple1=(1,3,5,7,2)
print(myTuple1)1,3,5,7,2myTuple2=myTuple1
print(myTuple2)myTuple3=tuple("Data")
myTuple3myTuple4=1,3,5,7,2
print(myTuple4)
运行结果:
(1, 3, 5, 7, 2)
(1, 3, 5, 7, 2)
(1, 3, 5, 7, 2)
('D', 'a', 't', 'a')
(1, 3, 5, 7, 2)
2 主要特征
运行程序:
1,3,5,7,2 #myTuple=1,3,5,7,2
#myTuple[2]=100
#1.元组与列表的区别:前者为【不可变对象】,后者为【不可变对象】
# 2. myTuple=1,3,5,7,2
# 3.myTuple[2]=100 #报错,原因:【元组】为不可变对象。myList=[1,3,5,7,2]
myList[2]=100#将元组中坐标为2值改为100
myListmyTuple=1,3,5,7,2
myTuple[2:5] #第3到5个myTuple=1,3,5,7,2
len(myTuple)#元组长度myTuple=1,3,5,7,2
print(sorted(myTuple)) #排序#myTuple=1,3,5,7,2
#myTuple.sort() # 1 #【注意】与列表不同的是,Python的元组无.sort()方法,原因:元组为不可变对象。#1 myTuple=1,3,5,7,2#3 myTuple.sort()#【提示】报错,原因:元组无此方法。myTuple=1,3,5,7,2
5 in myTuple #判断5是否在元组内myTuple=1,3,5,7,2
myTuple.count(11)#统计数值11出现频次myTuple=1,3,5,7,2
x1,x2,x3,x4,x5=myTuple #元组作为变量赋值
x2
myList1 = [21,22,23,24,25,26,27,28,29]
myList1myList1[1:8] #第2个到第个myList1[1:8:2] #步长为2myList1[:5] #第1个到第5个myList1[:] #所有myList1[2:] #第3个到最后myList1[:-1] #第1个到倒数第2个
运行结果:
(1, 3, 5, 7, 2)
[1, 3, 100, 7, 2]
(5, 7, 2)
5
[1, 2, 3, 5, 7]
True
0
3
3 基本用法
运行程序:
x,y,z =1,2,3
print(x,y,z)myTuple=(1,5,6,3,4)
print(myTuple)
print(len(myTuple))
print(max(myTuple))myTuple=(11,12,13,12,11,11)
a1,a2,a3,a4,a5,a6=myTuple
a3myTuple=(11,12,13,12,11,11)
myTuple.count(11)
运行结果:
1 2 3
(1, 5, 6, 3, 4)
5
6
13
3
4 应用场景
运行程序:
def func(args1,*args2): #带*:元组形参,接收不定长实参print(args1)print(args2)
func("a","b","c","d","e","f")def func(args1,**args2):print(args1)print(args2)
func("a",x1="b",x2="c",x3="d",x4="e",x5="f")#带**:字典def func():return 1,2,3,4,5
func()1,2x=1
y=2
x,y=y,x
print(x,y)
运行结果:
a
('b', 'c', 'd', 'e', 'f')
a
{'x1': 'b', 'x2': 'c', 'x3': 'd', 'x4': 'e', 'x5': 'f'}
(1, 2, 3, 4, 5)
(1, 2)
2 1['c', 'h', 'a', 'o', 'l', 'e', 'm', 'e', 'n']
相关文章:

【Python操作基础】——元组
🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972 个人介绍: 研一|统计学|干货分享 擅长Python、Matlab、R等主流编程软件 累计十余项国家级比赛奖项,参与研究经费10w、40w级横向 文…...

光伏投融资该如何计算?
光伏投融资是光伏产业发展过程中的重要环节,其计算涉及到多个方面,包括项目规模、预期收益、成本分析、风险评估等。合理的投融资计算能够为光伏项目的实施提供资金保障,同时也能够降低投资风险,提高项目的经济效益。 首先&#x…...

【更新中】Leetcode中遇到的最短路径算法
dijsktra算法模板: def dijkstra(x):#x表示出发点dis[inf]*n #dis记录从x出发到各个点的最短距离,初始化为infdis[x]0 #源点到自己的距离为0vis[False]*n #检查各个点是否访问过for _ in range(n-1): #检查除了源点的其他n-1个点,更新dis…...

Git学习笔记之基础
本笔记是阅读《git pro》所写,仅供参考。 《git pro》网址https://git-scm.com/book/en/v2 git官网 https://git-scm.com/ 一、git起步 1.1、检查配置信息 git config --list查看所有的配置以及它们所在的文件 git config --list --show-origin可能有重复的变量名…...

STCubeIDE 编译bootloader
头文件重复引用解决办法。 参考:STM32CubeIDE IAP原理讲解,及UART双APP交替升级IAP实现-CSDN博客 移植到Air32时,RAM的大小(无论boot程序还是app 程序) 尽量不动,如果动了会影响最终的 APP 跳转 flash 大小可以随意修改…...

Python学习:函数
函数定义 在Python中,函数(Function)是一组用于完成特定任务或计算的语句块。定义函数可以让我们将一段代码重用多次,提高代码的可读性和可维护性。以下是定义函数的基本语法和结构: def function_name(parameters):&…...

docker run 使用 -p 命令一直显示端口被占用
解决办法 将 -p 换成 --net host 例如: docker run --name one-api -d --restart always -p 3000:3000 -e TZ=Asia/Shanghai -v /root/oneapi/data:/data justsong/one-api # 换成 docker run --name one-api -d --restart always --net...

Rust 实战练习 - 1. 输入,输出,环境变量,字符,字符串
目标: 获取程序命令行参数标准输入输出获取环境变量字符串,字符初步学习 cargo传递参数,需要加上-- use std::{env, ffi::OsString, io, io::Write};fn main() {println!("OS Env: {:?} > {:?}", env::current_dir().unwra…...
)
RuoYi-Vue-Plus(登录流程)
一、前端登录请求 登录按钮: src\views\login.vue 页面中登录片段,调用了handleLogin 方法,如下: @click.native.prevent="handleLogin" <el-button:loading="loading"size="medium"type="primary"style="width:100%;&qu…...

【数学】 【分数】 【字符串】972. 相等的有理数
本文涉及知识点 数学 分数 字符串 LeetCode972. 相等的有理数 给定两个字符串 s 和 t ,每个字符串代表一个非负有理数,只有当它们表示相同的数字时才返回 true 。字符串中可以使用括号来表示有理数的重复部分。 有理数 最多可以用三个部分来表示&…...

【4】DongshanPI-Seven 应用开发_文件IO
目录 1.文件IO1.1 文件IO分类1.2 查看系统调用IO用法 2. open 函数3. write 函数4. read 函数5 dup函数 1.文件IO 1.1 文件IO分类 在Linux系统中,一切都是“文件”:普通文件、驱动程序、网络通信等。所有的操作都是通过文件IO来操作的。 在Linux操作文…...

SEO 的未来:GPT 和 AI 如何改变关键词研究
谷歌Gemini与百度文心一言:AI训练数据的较量 介绍 想象一下,有一个工具不仅可以理解错综复杂的关键字网络,还可以预测搜索引擎查询的变化趋势。 这就是生成式预训练 Transformer (GPT) 和其他人工智能技术发挥作用的地方,以我们从…...
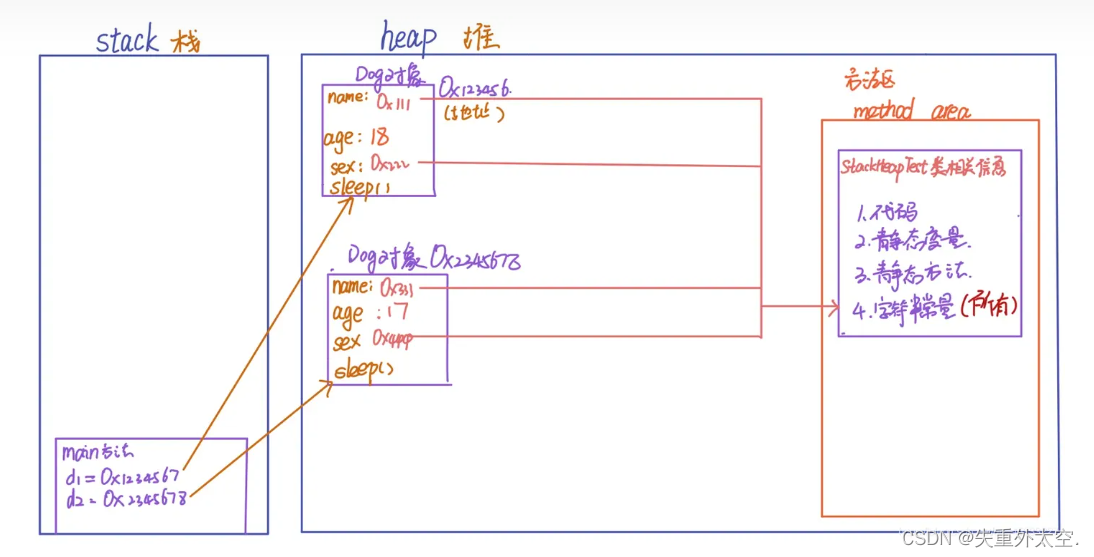
面试八股文之JAVA基础
JAVA基础 DNS、CDN?如何实现对象克隆?父子类静态代码块, 非静态代码块, 构造方法执行顺序?String s new String("abc") 创建了几个对象, 分别放到哪里?OSI网络模型七层?应用层协议?http协议和https协议区别?传输层协…...

网络连接中——长连接和短连接详解
一、TCP功能 TCP在真正开始进行数据传输之前,Server 和 Client 之间必须建立一个连接。当数据传输完成后,双方不再需要这个连接时,就可以释放这个连接。 TCP连接的建立是通过三次握手,而连接的释放是通过四次挥手。所以说,每个TCP连接的建立和释放都是需要消耗资源和时间…...
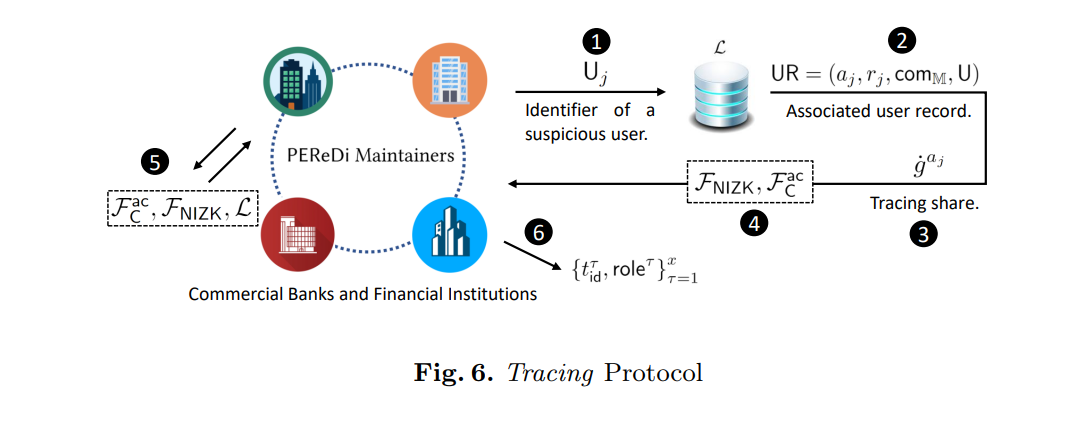
PEReDi 完全隐私的央行数字货币方案
第一个对完全隐私保护建模的方案,基于账户模型,要求交易双方都在线。 角色分类 中央银行 B B B:负责发行数字货币和货币政策,但不控制用户账户的状态,没有能力对交易的发送者或接收者进行去匿名化或披露与特定交易相…...

yolov5+pyside6+登录+用户管理目标检测可视化源码
一、软件简介 这是基于yolov5目标检测实现的源码,提供了用户登录功能界面; 用户需要输入正确的用户名和密码才可以登录。如果是超级管理员,可以修改普通用户的信息,并且在检测界面的右上角显示【管理用户】按钮。 支持图片、视频、…...

电脑如何设置个性便签 电脑个性便签分享
每次坐在电脑前,我都仿佛置身于一片信息的海洋。工作、生活、学习,方方面面的事情都需要我用心去记录。在这样一个快节奏的时代,电脑无疑成了我最得力的助手。但记事的时候,我总希望有一个既方便又有个性的工具,能让我…...
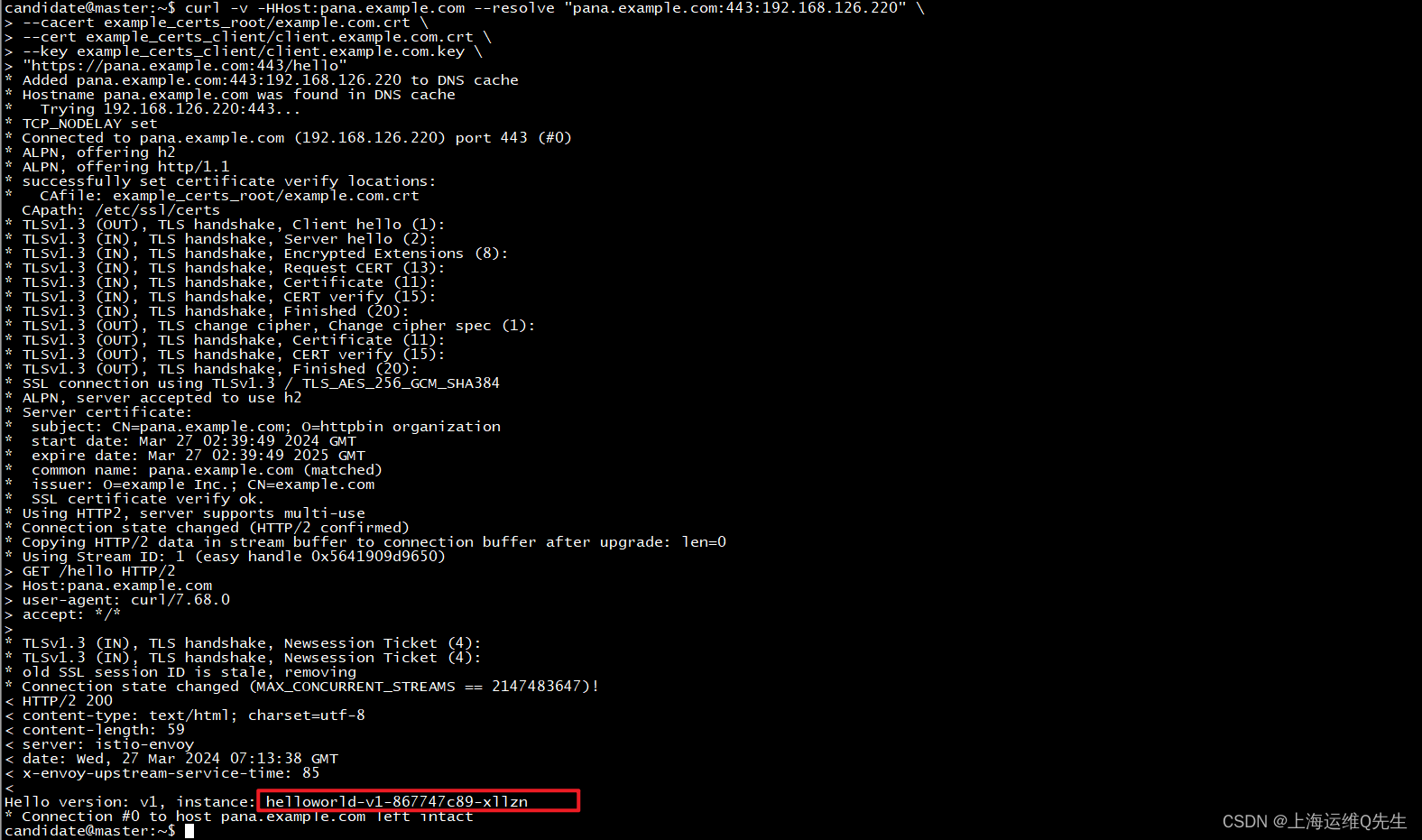
备考ICA----Istio实验12---配置双向TLS Istio Ingress Gateway实验
备考ICA----Istio实验12—配置双向TLS Istio Ingress Gateway实验 本实验部分配置延续上个Istio实验11 1. 重新配置secret 重新配置secret使其带有ca证书可以验证客户端证书是否合法 先删除原有secret,再配置新的secret # 删除原tls类型的secret kubectl -n istio-system d…...

SpringBoot 统一后端返回格式、处理全局异常
文章目录 引言I 统一标准格式1.1 定义返回标准格式1.2 定义状态码1.3 返回数据模型1.4 枚举定义1.5 Json序列化处理1.6 获取枚举字典II 处理全局异常2.1 全局异常处理器2.2 自定义异常2.3 请求数据模型III 预备知识:注解3.1 JsonInclude3.2 JsonIgnoreProperties...
C++学习基础版(一)
目录 一、C入门 1、C和C的区别 2、解读C程序 3、命名空间 4、输入输出 (1)cout输出流 (2)endl操纵符 (3)cin输入流 二、C表达式和控制语句 1、数据机构 特别:布尔类型bool 2、算数运…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...
