树状数组及应用
目录
1.树状数组的概念与基本编码
1.1.引导
1.2.lowbit(x)
1.3.树状数组的编码
2.树状数组的基本应用
2.1.单点修改+区间查询
2.2.区间修改+单点查询
例题:
2.3.区间修改+区间查询
例题:
如果数列A是静态不变的,那么处理前缀和复杂度为O(n),查询为O(1),但如果序列是动态变化的,如改变其中一个元素,那么就需要重新计算前缀和,如果每次查询都有变化,那么复杂度会大幅度增加。
有两种数据结构可以高效的处理这个问题:树状数组与线段树。
1.树状数组的概念与基本编码
1.1.引导
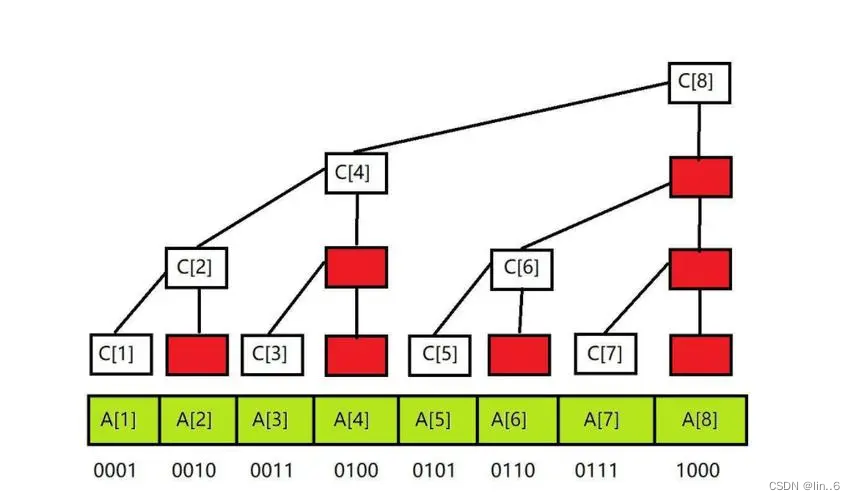
如图所示,c[1] = A[1], c[2] = c[1] + A[2], c[3] = A[3], c[4] = c[2] + c[3] + A[4], ... , c[8] = c[4] + c[6] + c[7] + A[8]。
利用c数组可以高效的完成以下两个操作。
(1)查询,即求前缀和sum。
(2)维护,即元素a发生变化时,能以O()的高效率修改c[] 的值。
结论:
(1)查询过程是每次去掉二进制的最后一个1。例如,求sum[7]:
- sum[7] += c[7]
- 7的二进制是111,去掉最后一个1,得110,即c[6],所以sum[7] += c[6]
- 110,去掉最后一个1,得100,sum[7] += c[4]
- 100,去掉最后一个1就没有了
故sum[7] = c[7] + c[6] + c[4]
(2)维护的过程是每次在二进制最后的1上加1。例如,更新a[3]:
- 3的二进制是11,在最后一个1上加1,得100,所以修改c[4];
- 100,在最后一个1上加1,得1000,所以修改c[8];
- 继续修改c[16],c[32]...
树状数组的关键就是找到最后一个1。
1.2.lowbit(x)
lowbit(x) = x & (-x),功能为找到x的二进制数最后一个1。其原理是利用负数的补码,例如x = 6 = 000110, 补 = 111010,那么x & (-x) = 10 = 2;
lowbit(x) 部分结果如下:
| x | x的二进制 | lowbit(x) | tree[x]数组 |
| 1 | 1 | 1 | tree[1] = a1 |
| 2 | 10 | 2 | tree[2] = a2 + a1 |
| 3 | 11 | 1 | tree[3] = a3 |
| 4 | 100 | 4 | tree[4] = a4 + a3+ a2+ a1 |
| 5 | 101 | 1 | tree[5] = a5 |
| 6 | 110 | 2 | tree[6] = a6 + a5 |
| 7 | 111 | 1 | tree[7] = a7 |
令m = lowbit(x),tree[x]的值是把和他前面共m个数相加的结果。
tree[]数组是通过lowbit计算出的树状数组,它能够以二分的复杂度存储一个数列的数据,具体的说,tree[x]存储的是区间[x - lowbit(x) + 1, x]的每个数的和。
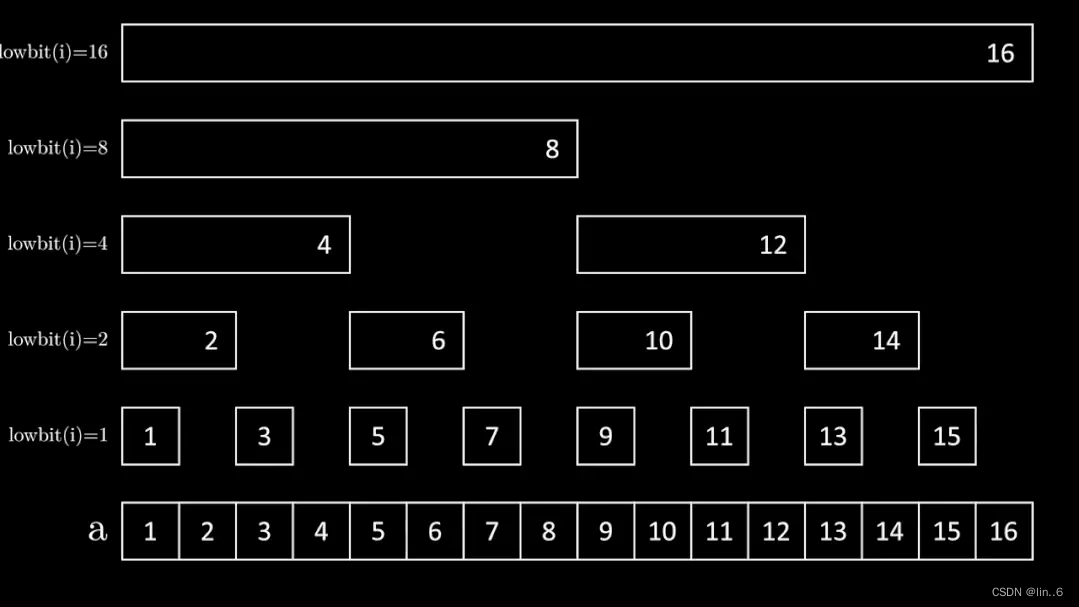
1.3.树状数组的编码
下面给出单点修改+区间查询的代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define lowbit(x) (x & (-x))
const int N = 1000;
int tree[N];
void update(int x, int d) {//单点修改,修改玄素a[x],a[x] = a[x] + dwhile (x <= N) {tree[x] += d;x += lowbit(x);}
}
ll sum(int x) {//查询前缀和:返回前缀和sum = a[1] + a[2] + .., + a[x]ll ans = 0;while (x > 0) {ans += tree[x];x -= lowbit(x);}return ans;
}
void solve() {int n;cin >> n;vector<ll> a(n + 1, 0);//a[0]不用memset(tree, 0, sizeof(tree));for (int i = 1; i <= n; i++) {cin >> a[i];update(i, a[i]);}//查询区间和:cout << "Old : sum([1,n-1]):" << sum(n - 1) - sum(0) << endl;//模拟一次修改,a[n-1] + 100update(n - 1, 100);cout << "New : sum([1,n-1]):" << sum(n - 1) - sum(0) << endl;
}
int main() {ios::sync_with_stdio;cin.tie(0);cout.tie(0);solve();return 0;
}
/*
输入:
10
4 5 6 7 8 9 10 11 12 13
输出:
Old : sum([1,n-1]):72
New : sum([1,n-1]):172
*/此代码过程:
(1)初始化:先清空数组tree,然后读取a数组每一个元素,用update() 逐步处理这n个数,得到tree[]数组;
(2)求前缀和:用sum()计算,求和基于tree数组;
(3)单点修改:执行update()函数,修改数组tree[]。
2.树状数组的基本应用
2.1.单点修改+区间查询
1.1.3.树状数组的编码已经给出
2.2.区间修改+单点查询
利用差分是前缀和的逆运算来求解
例题:
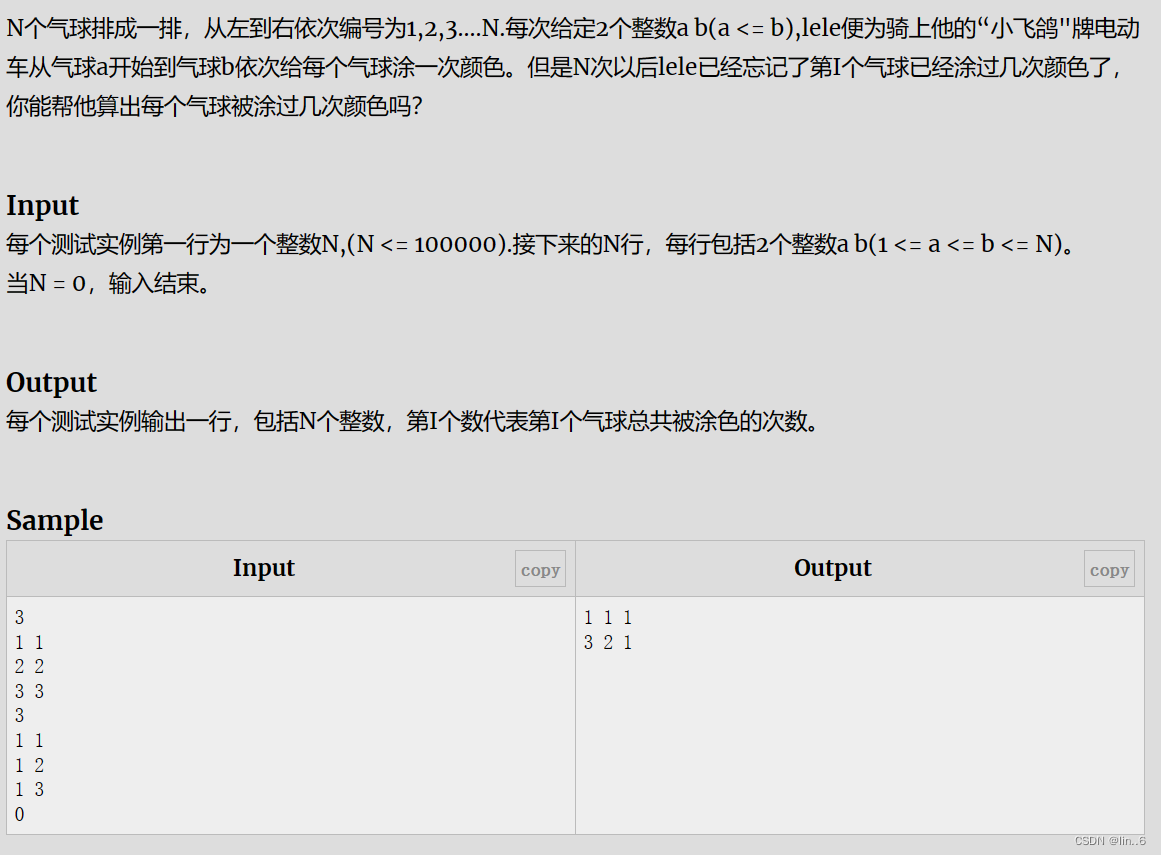
两种解法:
第一种,单纯的差分数组
#include<bits/stdc++.h>
using namespace std;
int n, a, b, diff[100002];
int main() {ios::sync_with_stdio(false);cin.tie(0);while (cin >> n && n != 0) {for (int i = 0; i <= n; i++) {diff[i] = 0;}for (int i = 0; i < n; i++) {cin >> a >> b;diff[a] += 1;diff[b + 1] -= 1;}diff[1] += diff[0];cout << diff[1];for (int i = 2; i <= n; i++) {diff[i] += diff[i - 1];cout << ' ' << diff[i];}}return 0;
}第二种,利用树状数组
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define lowbit(x) (x & (-x))
const int N = 100010;
int tree[N];
void update(int x, int d) {while (x <= N) {tree[x] += d;x += lowbit(x);}
}
ll sum(int x) {ll ans = 0;while (x > 0) {ans += tree[x];x -= lowbit(x);}return ans;
}
void solve() {int n;while (cin >> n && n != 0) {memset(tree, 0, sizeof(tree));for (int i = 1; i <= n; i++) {int L, R;cin >> L >> R;update(L, 1);update(R + 1, -1);}for (int i = 1; i <= n; i++) {if (i != n)cout << sum(i) << ' ';else cout << sum(i) << endl;}}
}
int main() {ios::sync_with_stdio;cin.tie(0);cout.tie(0);solve();return 0;
}2.3.区间修改+区间查询
完成区间修改需要一个tree,区间查询也需要一个tree,所以可以利用两个tree达成此要求
=
=
所以可以分别处理d和(i-1)d两个数组的树状数组
例题:


#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define lowbit(x) (x & (-x))
const int N = 100010;
ll tree1[N], tree2[N];
void update1(ll x, ll d) {while (x <= N) {tree1[x] += d;x += lowbit(x);}
}
ll sum1(ll x) {ll ans = 0;while (x > 0) {ans += tree1[x];x -= lowbit(x);}return ans;
}
void update2(ll x, ll d) {while (x <= N) {tree2[x] += d;x += lowbit(x);}
}
ll sum2(ll x) {ll ans = 0;while (x > 0) {ans += tree2[x];x -= lowbit(x);}return ans;
}
void solve() {ll n, m;memset(tree1, 0, sizeof(tree1));memset(tree2, 0, sizeof(tree2));cin >> n >> m;ll old = 0, a;for (int i = 1; i <= n; i++) {cin >> a;update1(i, a - old);update2(i, (i - 1) * (a - old));old = a;}while (m--) {ll q, L, R, d;cin >> q;if (q == 1) {cin >> L >> R >> d;update1(L, d);update1(R + 1, -d);update2(L, (L - 1) * d);update2(R + 1, -R * d);}else {cin >> L >> R;cout << R * sum1(R) - sum2(R) - (L - 1) * sum1(L - 1) + sum2(L - 1) << endl;}}
}
int main() {ios::sync_with_stdio;cin.tie(0);cout.tie(0);solve();return 0;
}相关文章:

树状数组及应用
目录 1.树状数组的概念与基本编码 1.1.引导 1.2.lowbit(x) 1.3.树状数组的编码 2.树状数组的基本应用 2.1.单点修改+区间查询 2.2.区间修改单点查询 例题: 2.3.区间修改+区间查询 例题: 如果数列A是静态不变的ÿ…...

HarmonyOS 应用开发案例
本帖下方集中了HarmonyOS Next应用开发时,会遇到的常见应用案例。后续会持续更新大量案例,帮助开发者快速学习。欢迎感兴趣的同学加入Q:454901491 72.手写绘制及保存图片案例(0319更新)(点此查看源码实现&…...
【C++ leetcode】双指针(专题完结)
15. 三数之和 题目 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的…...
动态代理大总结
1.开启EnableAspectJAutoProxy注解 @EnableAspectJAutoProxy注解【相当于加了个BeanPostProcessor】,会导入AspectJAutoProxyReqistrar这个类,会把AnnotationAwareAspectJAutoProxyCreator注册进spring容器中,注册进容器后还会看这两个属性的值【proxyTargetClass,exposeP…...

理解Harris角点检测的数学原理
Harris角点检测的数学原理 Harris角点检测基于图像的局部自相似性,它通过分析图像窗口在各个方向上移动时灰度变化的程度来识别角点,它通过计算每个像素点的Harris响应值来评估该点是否为角点。数学上,这种变化可以通过构建一个二次型函数来量化,该函数基于图像在x和y方向上…...
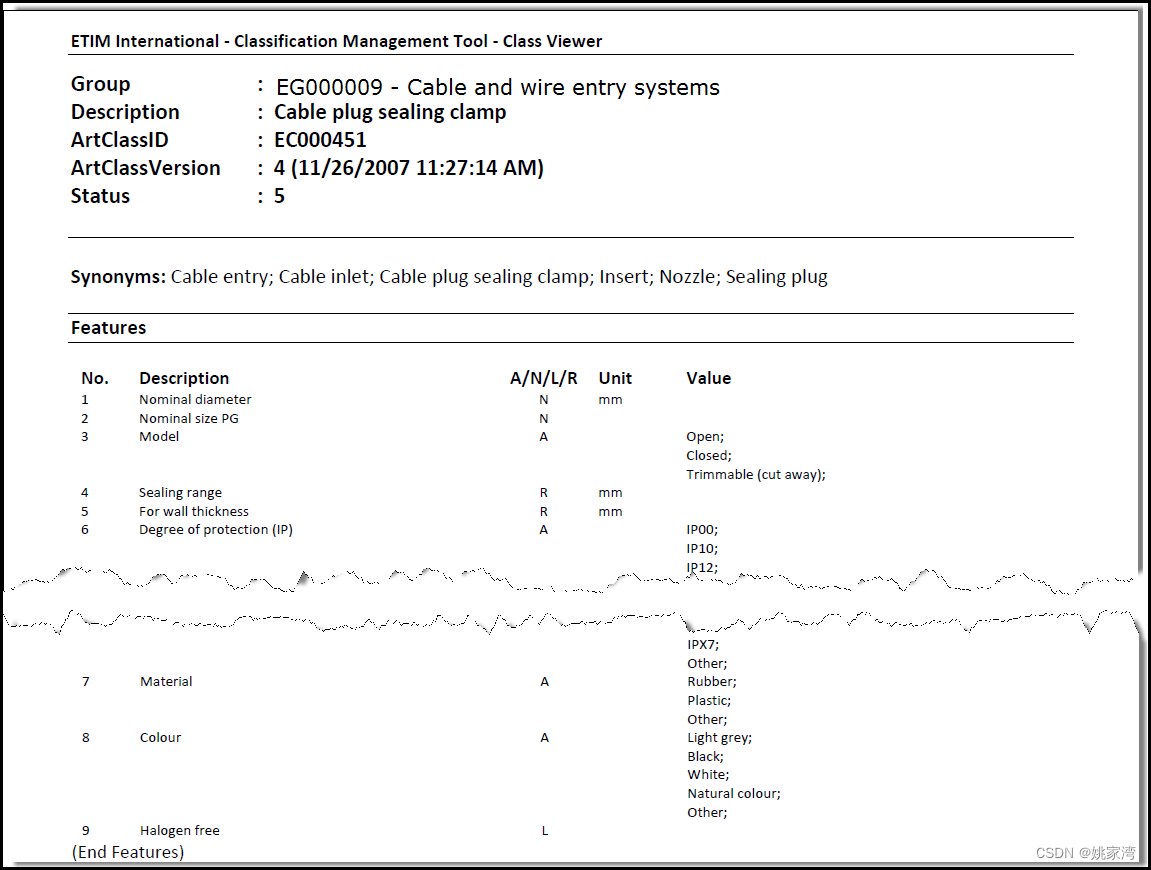
ETIM -国际贸易的产品分类标准
ETIM 是除了XML 国际交流标准BMEcat之外的国际贸易的产品分类标准。 什么是ETIM ? ETIM是一种基于分类识别共享和交换产品数据的格式。这种广泛使用的技术产品分类标准是为了构建 B2B 专业人员之间的信息流而制定的。 为什么选择ETIM? ETIM分类模型的开…...
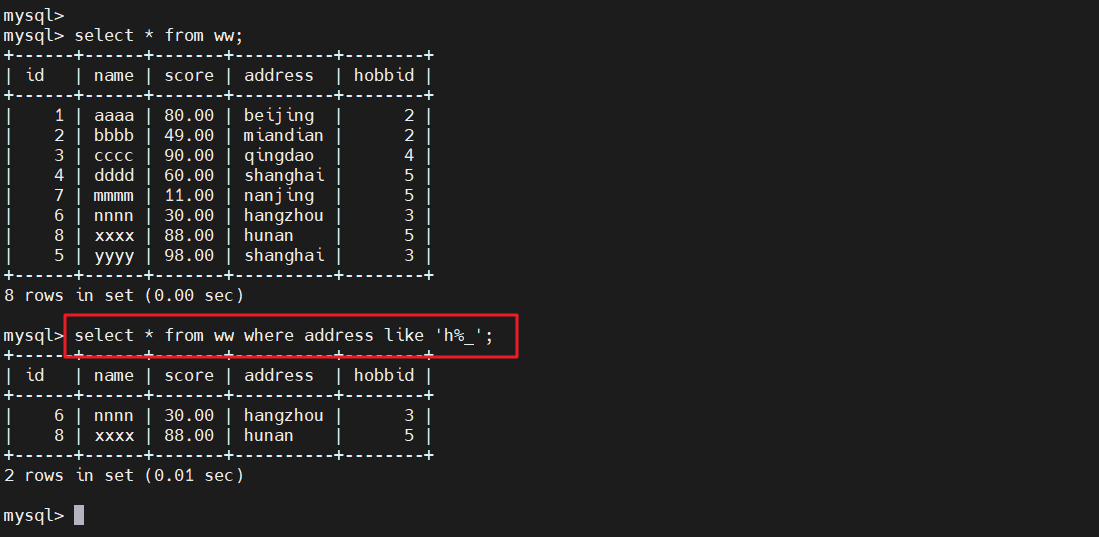
MySQL高阶SQL语句
文章目录 MySQL高阶SQL语句MySQL常用查询1、按关键字排序1.1 语法1.2 ASC和DESC1.3 对数据表中信息进行排序1.3.1 普通排序1.3.2 结合where进行条件过滤1.3.3 对多个字段进行排序 2、区间判断及查询不重复记录2.1 and/or —— 且/或2.1.1 普通查询2.1.2 嵌套/多条件查询 2.2 di…...

聊聊CSS
css 的介绍 学习目标 能够知道css的作用 1. css 的定义 css(Cascading Style Sheet)层叠样式表,它是用来美化页面的一种语言。 没有使用css的效果图 使用css的效果图 2. css 的作用 美化界面, 比如: 设置标签文字大小、颜色、字体加粗等样式。 控制页面布局, 比如…...
C语言 青蛙跳台阶问题
目录 编辑 1.问题描述 2.问题分析 3.全部代码 4.结语 1.问题描述 一只青蛙可以一次跳一级台阶,也可以一次跳两级台阶,如果青蛙要跳上n级台阶有多少种跳法? 2.问题分析 当台阶只有一级时,只能跳一级,所以只有一…...
【Django开发】前后端分离美多商城项目第3篇:用户部分,1. 后端接口设计:【附代码文档】
美多商城项目4.0文档完整教程(附代码资料)主要内容讲述:美多商城,项目准备1.B2B–企业对企业,2.C2C–个人对个人,3.B2C–企业对个人,4.C2B–个人对企业。项目准备,配置1. 修改settings/dev.py 文件中的路径信息,2. INS…...

DHCP snooping、DHCP安全及威胁防范
DHCP snooping、DHCP安全及威胁防范 [SW1]display dhcp snooping user-bind all,查看DHCP snooping表项。 DHCP snooping: 表项是通过服务器发送给客户端的ACK报文生成的。 只能在交换机上开启,路由器不支持,并且建议在接入交…...
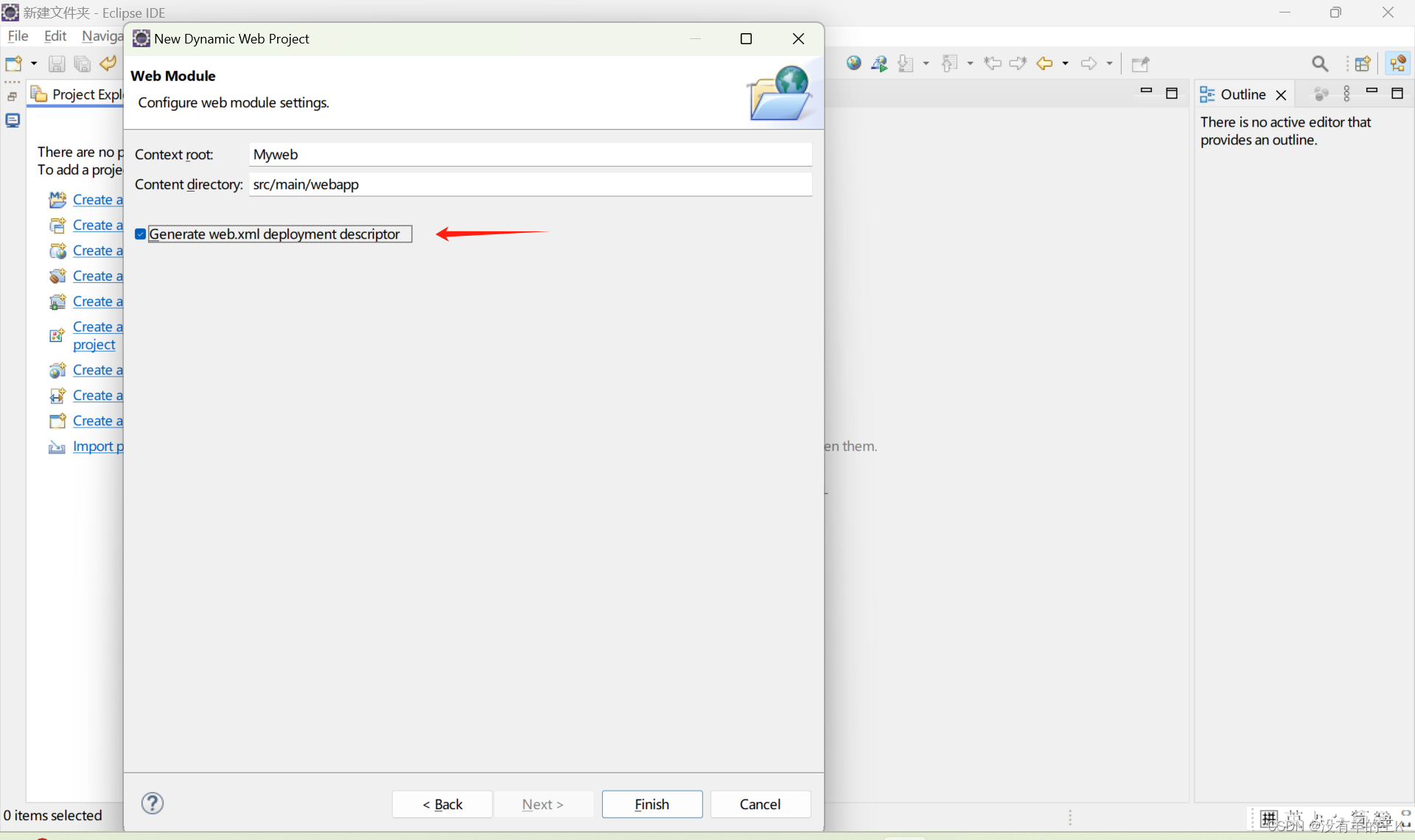
用eclipse创建Web项目,通过Servlet实现Web访问的功能。
要使用Eclipse和Tomcat 10创建一个简单的Web项目,并通过Servlet实现Web访问功能,你需要遵循以下详细步骤: 1. 安装和配置Eclipse和Tomcat 10 确保你已经安装了Eclipse IDE for Java EE Developers和Tomcat 10。如果还没有安装,请…...
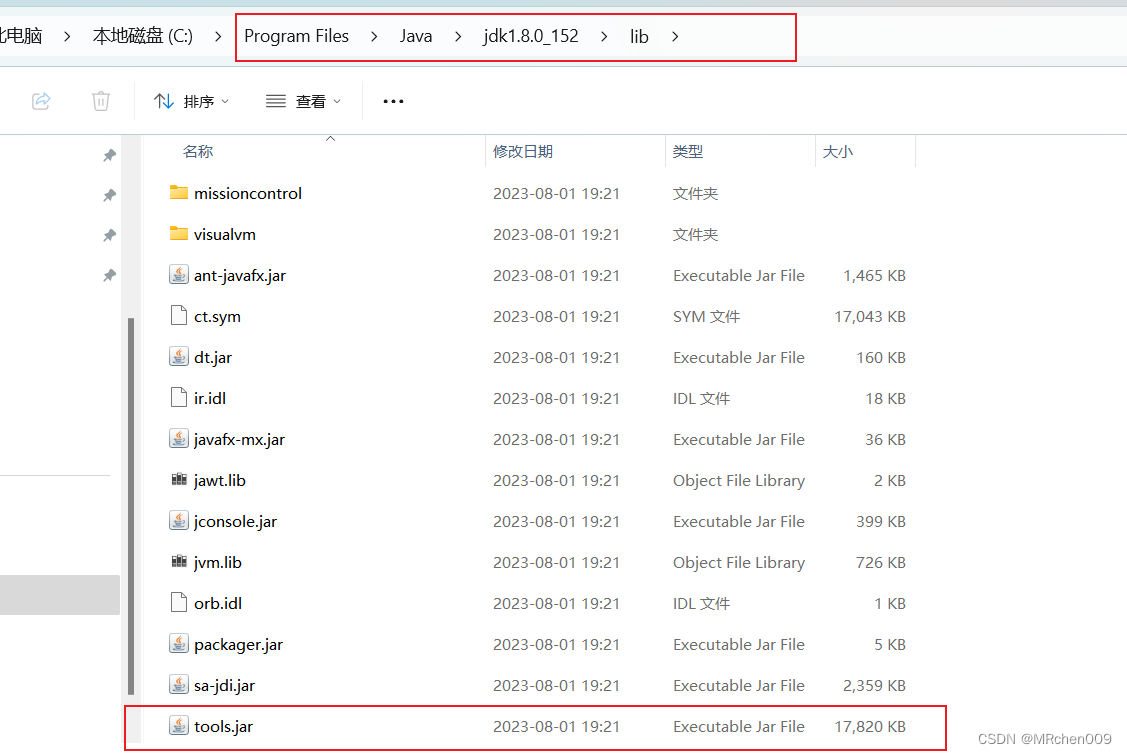
tools.jar下载 Unable to create schema compiler
网上查找了一堆下载tools.jar的都是忽悠人的,在这我就直接告诉大家,直接在电脑的JDK安装路径下的lib文件下复制就可以了。如果没有的话可以diss我我发给你...
初始化(3))
【0278】checkpointer 共享内存(CheckpointerShmem)初始化(3)
0. 关于checkpointer 检查指针是Postgres 9.2的新特性。它处理所有检查点。自上次检查点以来,检查点在经过一定时间后自动分发,并且还可以发出信号来执行请求的检查点。(GUC参数要求每隔这么多WAL段就有一个检查点,这是通过后端在填充WAL段时发出信号来实现的; checkpointer…...
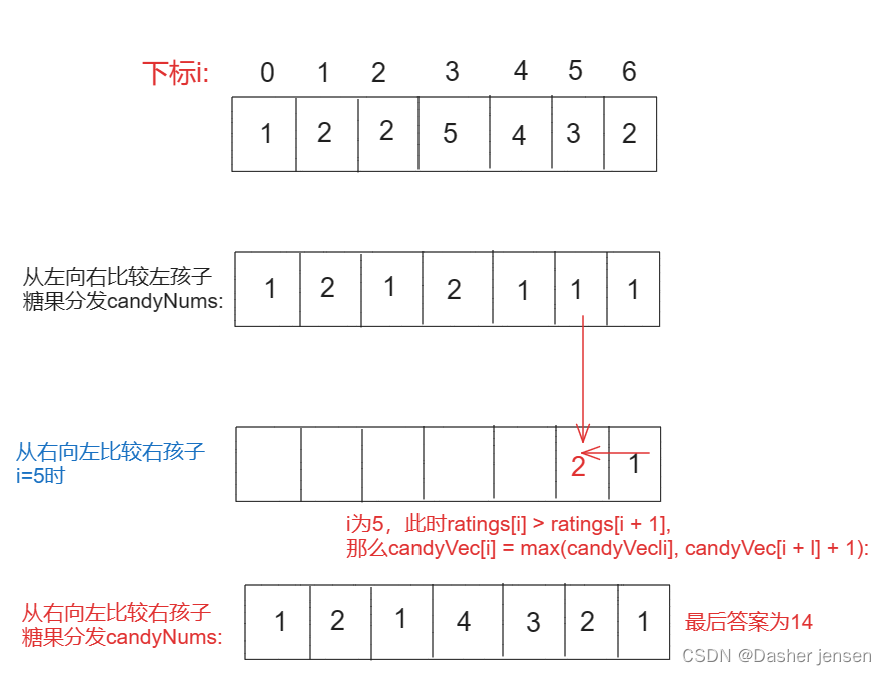
算法打卡day29|贪心算法篇03|Leetcode 1005.K次取反后最大化的数组和、134. 加油站、135. 分发糖果
算法题 Leetcode 1005.K次取反后最大化的数组和 题目链接:1005.K次取反后最大化的数组和 大佬视频讲解:K次取反后最大化的数组和视频讲解 个人思路 思路清晰,因为是取反当然是取越小的负数越好,那么先按绝对值排序。如果是负数就取反&#…...
【hexo博客6】自定义域名 购买、配置、更新部署
【hexo博客6】自定义域名 购买、配置、更新部署 写在最前面自定义域名购买域名DNS配置Github 配置 更新部署博客 🌈你好呀!我是 是Yu欸 🌌 2024每日百字篆刻时光,感谢你的陪伴与支持 ~ 🚀 欢迎一起踏上探险之旅&#…...

Django使用pyJwt进行token校验
1.登录成功后返回token,这里使用authenticate进行校验是否存在该用户 def login(request):try:data json.loads(request.body)username data.get(username)password data.get(password)if not all([username, password]):return to_response(status400, msg参数…...
)
❤️算法笔记❤️-(每日一刷-26、删除有序数组的重复项)
文章目录 题目思路解法 题目 给你一个 非严格递增排列 的数组 nums ,请你** 原地** 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums 的唯…...

银河麒麟系统安装设备类型选择lvm简单模式之后,数据写入导致失败导致系统重启无法正常加载
银河麒麟系统安装设备类型选择lvm简单模式之后,数据写入导致失败导致系统重启无法正常加载 一 系统环境1.1 系统版本信息1.2 通过镜像安装的过程中选择设备类型选择的是lvm简单模式 二 问题描述三 问题修复过程3.1 挂载ISO镜像,引导到字符终端界面3.2 修…...
Mybatis-核心配置文件 / Mybatis增删改查
1. 核心配置文件 1.1. 概述 核心配置文件是MyBatis框架中用于集中定义全局配置信息的XML文件,其内部包含了一系列预设标签,用于设置数据库连接、对象映射、类型处理等关键参数。这些标签遵循特定的排列顺序,尽管并非所有标签都是强制性的&a…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...
