理解Harris角点检测的数学原理
Harris角点检测的数学原理
Harris角点检测基于图像的局部自相似性,它通过分析图像窗口在各个方向上移动时灰度变化的程度来识别角点,它通过计算每个像素点的Harris响应值来评估该点是否为角点。数学上,这种变化可以通过构建一个二次型函数来量化,该函数基于图像在x和y方向上的一阶导数(即图像的梯度),以及梯度的二次项的组合。
一、数学题目第一题
假设我们有一个图像区域的灰度函数 I ( x , y ) I(x, y) I(x,y),其中 x , y x, y x,y 分别是图像上的横纵坐标。我们对 I ( x , y ) I(x, y) I(x,y) 在点 ( x 0 , y 0 ) (x_0, y_0) (x0,y0) 附近进行泰勒展开,忽略二阶及以上项,考虑一个小窗口移动了 ( Δ x , Δ y ) (\Delta x, \Delta y) (Δx,Δy) 后的灰度变化 E ( Δ x , Δ y ) E(\Delta x, \Delta y) E(Δx,Δy):
E ( Δ x , Δ y ) = ∑ x , y w ( x , y ) [ I ( x + Δ x , y + Δ y ) − I ( x , y ) ] 2 E(\Delta x, \Delta y) = \sum_{x, y} w(x, y) [I(x + \Delta x, y + \Delta y) - I(x, y)]^2 E(Δx,Δy)=x,y∑w(x,y)[I(x+Δx,y+Δy)−I(x,y)]2
其中, w ( x , y ) w(x, y) w(x,y) 是窗口函数,通常为高斯窗口,用于给窗口内的像素点赋予权重。
- 请简化上述 E ( Δ x , Δ y ) E(\Delta x, \Delta y) E(Δx,Δy) 表达式,展示如何利用图像的梯度( I x , I y I_x, I_y Ix,Iy)和高斯权重来近似计算 E ( Δ x , Δ y ) E(\Delta x, \Delta y) E(Δx,Δy)。
- 说明Harris角点检测中“角点”的数学特性是什么?
- 如果给定一个简单的图像区域,其中 I x = [ 1 0 0 − 1 ] I_x = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} Ix=[100−1] 和 I y = [ 0 1 − 1 0 ] I_y = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} Iy=[0−110],并假设 w ( x , y ) = 1 w(x, y) = 1 w(x,y)=1 (即不考虑权重),求该区域的Harris响应函数值。
解答过程
-
简化 E ( Δ x , Δ y ) E(\Delta x, \Delta y) E(Δx,Δy):
通过泰勒展开,我们可以得到:
I ( x + Δ x , y + Δ y ) ≈ I ( x , y ) + I x ( x , y ) Δ x + I y ( x , y ) Δ y I(x + \Delta x, y + \Delta y) \approx I(x, y) + I_x(x, y) \Delta x + I_y(x, y) \Delta y I(x+Δx,y+Δy)≈I(x,y)+Ix(x,y)Δx+Iy(x,y)Δy
将其代入 E ( Δ x , Δ y ) E(\Delta x, \Delta y) E(Δx,Δy) 的表达式中,并简化:
E ( Δ x , Δ y ) ≈ ∑ x , y w ( x , y ) [ I x Δ x + I y Δ y ] 2 E(\Delta x, \Delta y) \approx \sum_{x, y} w(x, y) [I_x \Delta x + I_y \Delta y]^2 E(Δx,
相关文章:

理解Harris角点检测的数学原理
Harris角点检测的数学原理 Harris角点检测基于图像的局部自相似性,它通过分析图像窗口在各个方向上移动时灰度变化的程度来识别角点,它通过计算每个像素点的Harris响应值来评估该点是否为角点。数学上,这种变化可以通过构建一个二次型函数来量化,该函数基于图像在x和y方向上…...
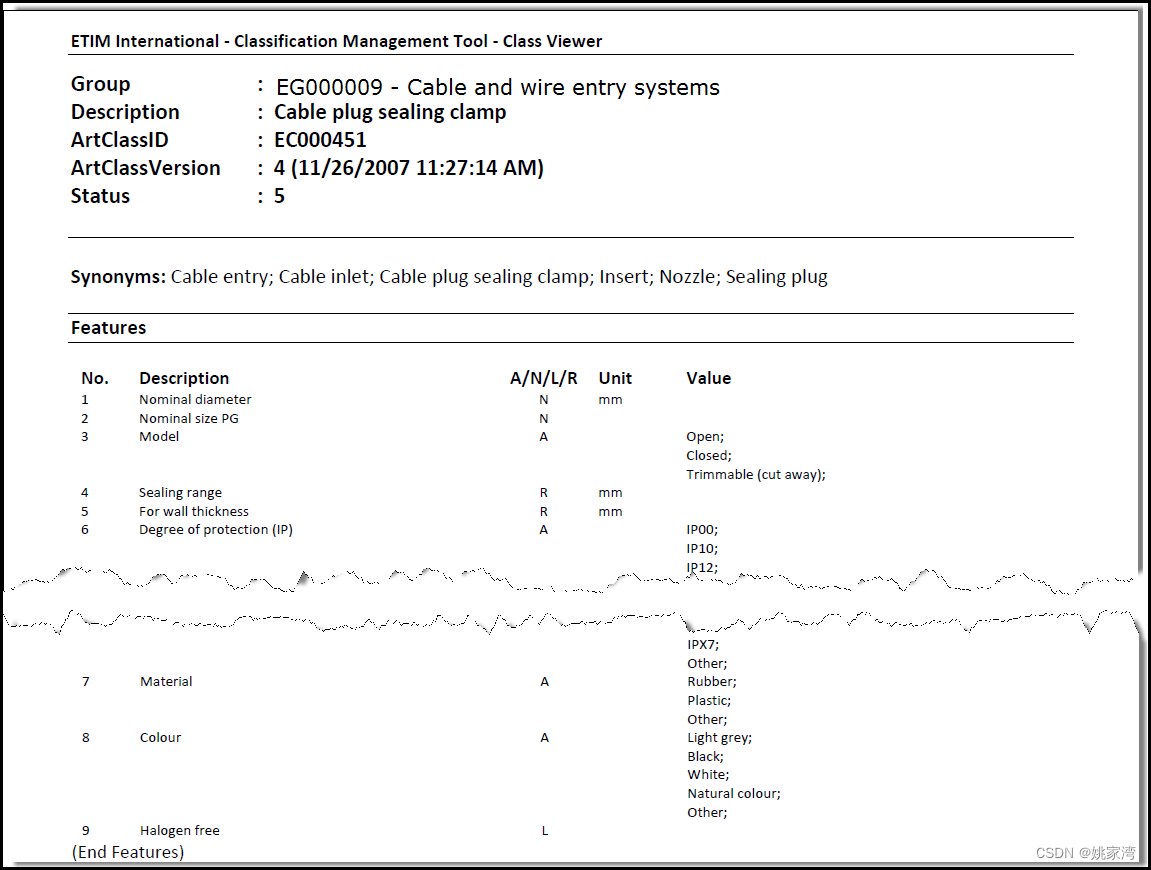
ETIM -国际贸易的产品分类标准
ETIM 是除了XML 国际交流标准BMEcat之外的国际贸易的产品分类标准。 什么是ETIM ? ETIM是一种基于分类识别共享和交换产品数据的格式。这种广泛使用的技术产品分类标准是为了构建 B2B 专业人员之间的信息流而制定的。 为什么选择ETIM? ETIM分类模型的开…...
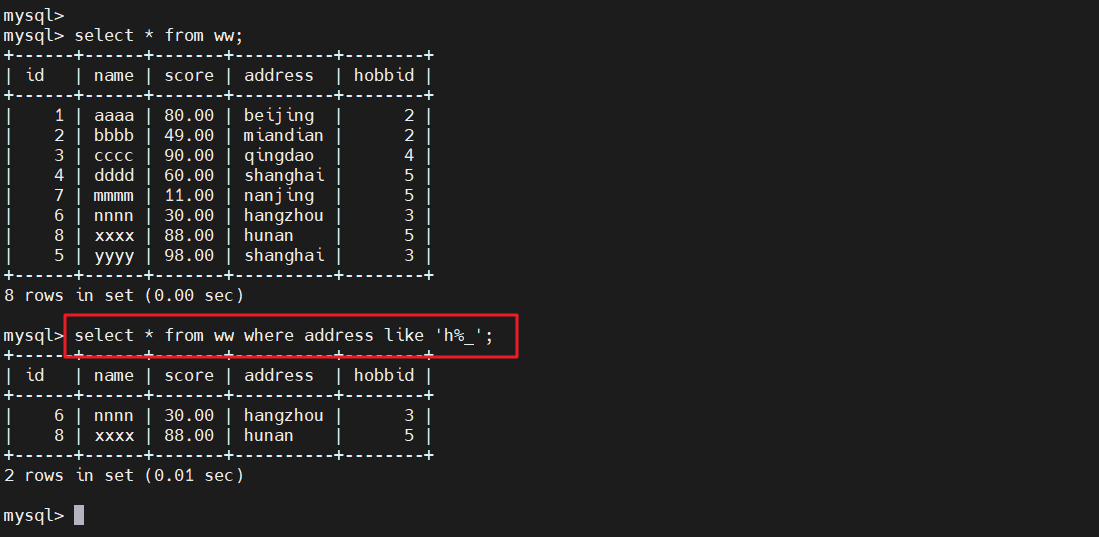
MySQL高阶SQL语句
文章目录 MySQL高阶SQL语句MySQL常用查询1、按关键字排序1.1 语法1.2 ASC和DESC1.3 对数据表中信息进行排序1.3.1 普通排序1.3.2 结合where进行条件过滤1.3.3 对多个字段进行排序 2、区间判断及查询不重复记录2.1 and/or —— 且/或2.1.1 普通查询2.1.2 嵌套/多条件查询 2.2 di…...

聊聊CSS
css 的介绍 学习目标 能够知道css的作用 1. css 的定义 css(Cascading Style Sheet)层叠样式表,它是用来美化页面的一种语言。 没有使用css的效果图 使用css的效果图 2. css 的作用 美化界面, 比如: 设置标签文字大小、颜色、字体加粗等样式。 控制页面布局, 比如…...
C语言 青蛙跳台阶问题
目录 编辑 1.问题描述 2.问题分析 3.全部代码 4.结语 1.问题描述 一只青蛙可以一次跳一级台阶,也可以一次跳两级台阶,如果青蛙要跳上n级台阶有多少种跳法? 2.问题分析 当台阶只有一级时,只能跳一级,所以只有一…...
【Django开发】前后端分离美多商城项目第3篇:用户部分,1. 后端接口设计:【附代码文档】
美多商城项目4.0文档完整教程(附代码资料)主要内容讲述:美多商城,项目准备1.B2B–企业对企业,2.C2C–个人对个人,3.B2C–企业对个人,4.C2B–个人对企业。项目准备,配置1. 修改settings/dev.py 文件中的路径信息,2. INS…...

DHCP snooping、DHCP安全及威胁防范
DHCP snooping、DHCP安全及威胁防范 [SW1]display dhcp snooping user-bind all,查看DHCP snooping表项。 DHCP snooping: 表项是通过服务器发送给客户端的ACK报文生成的。 只能在交换机上开启,路由器不支持,并且建议在接入交…...
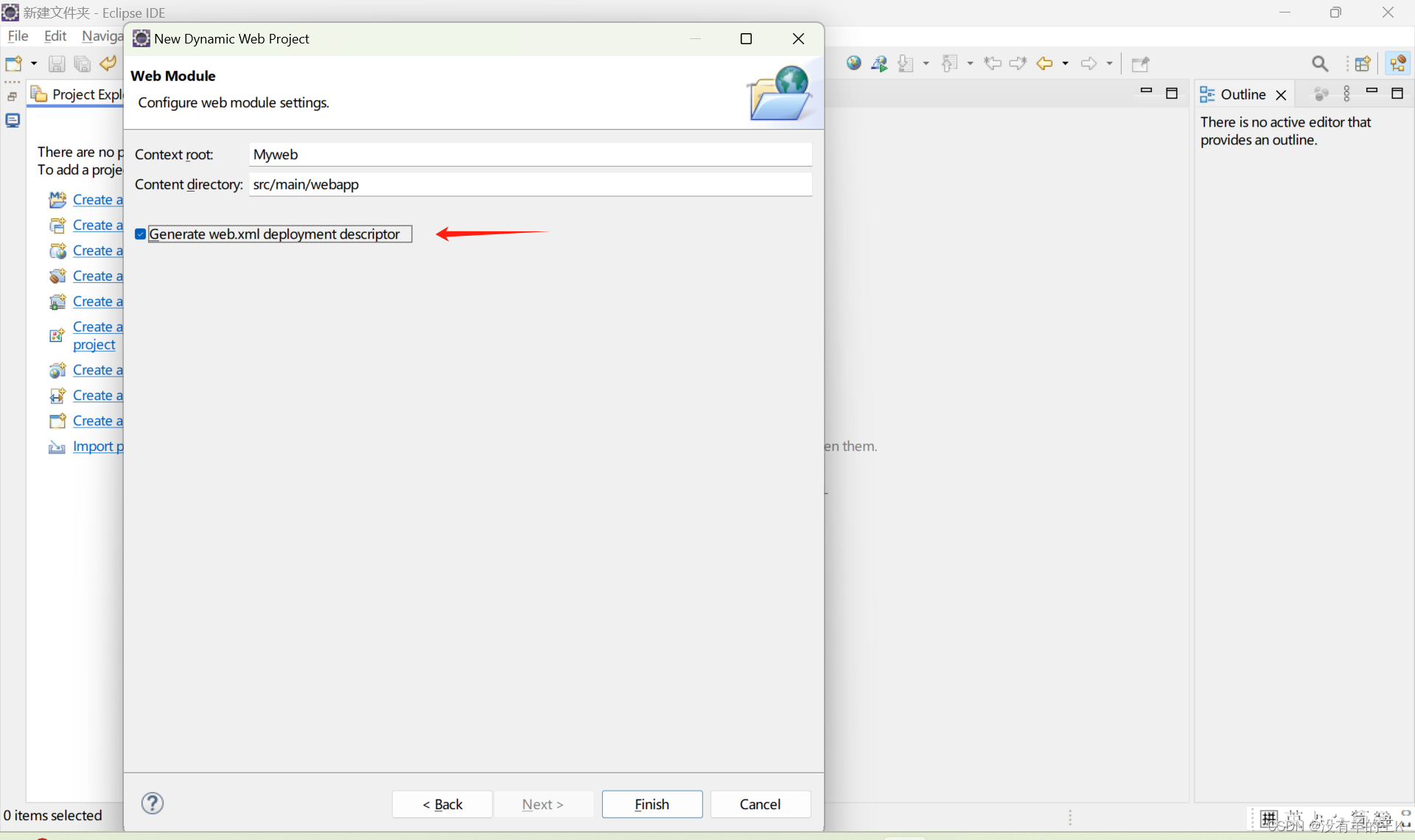
用eclipse创建Web项目,通过Servlet实现Web访问的功能。
要使用Eclipse和Tomcat 10创建一个简单的Web项目,并通过Servlet实现Web访问功能,你需要遵循以下详细步骤: 1. 安装和配置Eclipse和Tomcat 10 确保你已经安装了Eclipse IDE for Java EE Developers和Tomcat 10。如果还没有安装,请…...
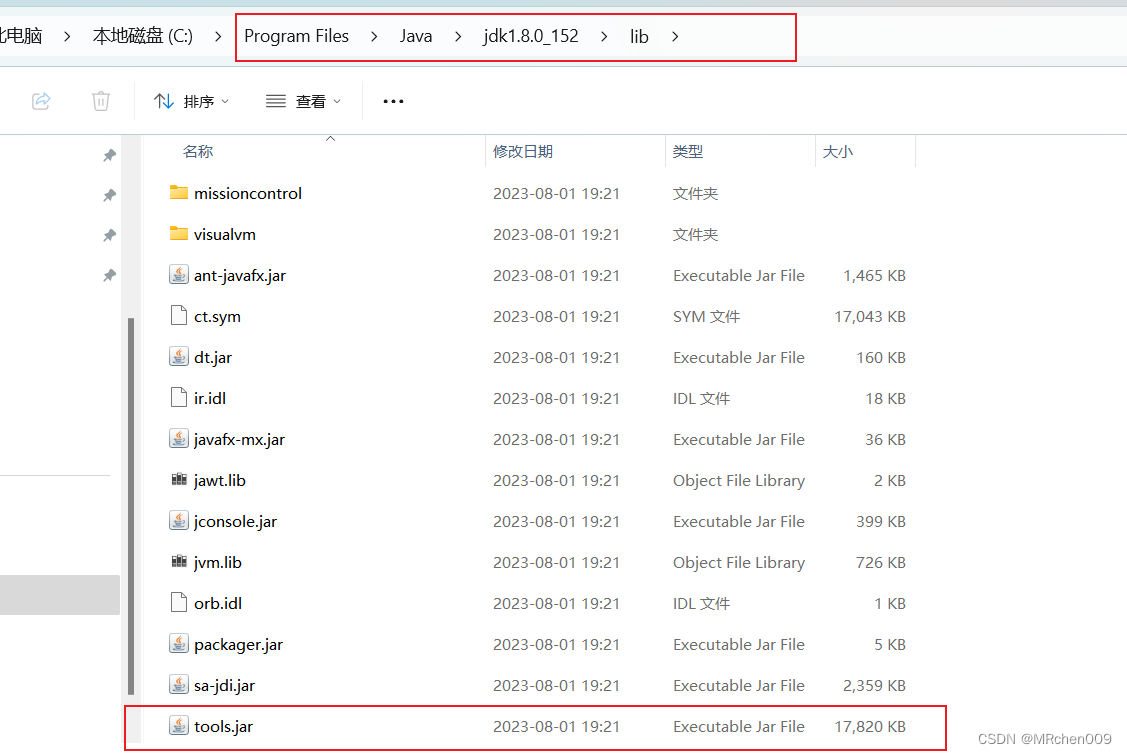
tools.jar下载 Unable to create schema compiler
网上查找了一堆下载tools.jar的都是忽悠人的,在这我就直接告诉大家,直接在电脑的JDK安装路径下的lib文件下复制就可以了。如果没有的话可以diss我我发给你...
初始化(3))
【0278】checkpointer 共享内存(CheckpointerShmem)初始化(3)
0. 关于checkpointer 检查指针是Postgres 9.2的新特性。它处理所有检查点。自上次检查点以来,检查点在经过一定时间后自动分发,并且还可以发出信号来执行请求的检查点。(GUC参数要求每隔这么多WAL段就有一个检查点,这是通过后端在填充WAL段时发出信号来实现的; checkpointer…...
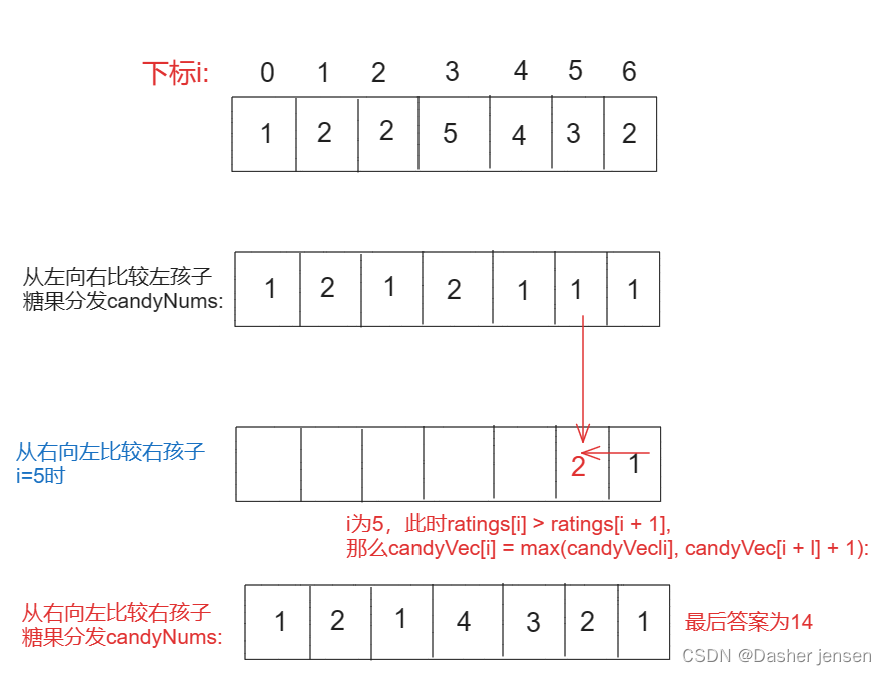
算法打卡day29|贪心算法篇03|Leetcode 1005.K次取反后最大化的数组和、134. 加油站、135. 分发糖果
算法题 Leetcode 1005.K次取反后最大化的数组和 题目链接:1005.K次取反后最大化的数组和 大佬视频讲解:K次取反后最大化的数组和视频讲解 个人思路 思路清晰,因为是取反当然是取越小的负数越好,那么先按绝对值排序。如果是负数就取反&#…...
【hexo博客6】自定义域名 购买、配置、更新部署
【hexo博客6】自定义域名 购买、配置、更新部署 写在最前面自定义域名购买域名DNS配置Github 配置 更新部署博客 🌈你好呀!我是 是Yu欸 🌌 2024每日百字篆刻时光,感谢你的陪伴与支持 ~ 🚀 欢迎一起踏上探险之旅&#…...

Django使用pyJwt进行token校验
1.登录成功后返回token,这里使用authenticate进行校验是否存在该用户 def login(request):try:data json.loads(request.body)username data.get(username)password data.get(password)if not all([username, password]):return to_response(status400, msg参数…...
)
❤️算法笔记❤️-(每日一刷-26、删除有序数组的重复项)
文章目录 题目思路解法 题目 给你一个 非严格递增排列 的数组 nums ,请你** 原地** 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums 的唯…...

银河麒麟系统安装设备类型选择lvm简单模式之后,数据写入导致失败导致系统重启无法正常加载
银河麒麟系统安装设备类型选择lvm简单模式之后,数据写入导致失败导致系统重启无法正常加载 一 系统环境1.1 系统版本信息1.2 通过镜像安装的过程中选择设备类型选择的是lvm简单模式 二 问题描述三 问题修复过程3.1 挂载ISO镜像,引导到字符终端界面3.2 修…...
Mybatis-核心配置文件 / Mybatis增删改查
1. 核心配置文件 1.1. 概述 核心配置文件是MyBatis框架中用于集中定义全局配置信息的XML文件,其内部包含了一系列预设标签,用于设置数据库连接、对象映射、类型处理等关键参数。这些标签遵循特定的排列顺序,尽管并非所有标签都是强制性的&a…...
)
Nginx(面试)
NGINX 速记问答 Q 什么是Nginx?它的主要特点是什么? A Nginx是一个高性能的开源Web服务器和反向代理服务器。它以高并发、低内存消耗和高稳定性著称。 Q Nginx与Apache Web服务器有什么区别? A Nginx与Apache相比,更适用于处…...

net::ERR_SSL_PROTOCOL_ERROR
小程序 发起网络请求 解决: 如果还没有申请SSL证书,那就直接把https请求改为http 测试可以用 上线不推荐...
)
BaseDao封装增删改查(超详解)
Hi i,m JinXiang ⭐ 前言 ⭐ 本篇文章主要介绍对数据库中表中的数据进行增改删查询,封装一个工具类(BaseDao)的详细使用以及部分理论知识 🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁 &…...

【Python操作基础】——元组
🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972 个人介绍: 研一|统计学|干货分享 擅长Python、Matlab、R等主流编程软件 累计十余项国家级比赛奖项,参与研究经费10w、40w级横向 文…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...
