Mashup-Math_Topic_One
Tutorial and Introspection
A Rudolf and 121
注意到第 1 1 1 位只能被第 2 2 2 位影响,以此类推位置,对于 a i a_i ai , 如果 < 0 < 0 <0 ,不合法 ; 否则, a i − = a i , a i + 1 − = 2 ∗ a i , a i + 2 − = a i a_i-=a_i,a_{i+1}-=2*a_i,a_{i+2}-=a_i ai−=ai,ai+1−=2∗ai,ai+2−=ai
操作到最后再检查一下 n − 1 n-1 n−1 跟 n n n 这两个位置
void solve(){cin >> n;for(int i = 1; i <= n; i ++){cin >> a[i];}for(int i = 1; i <= n - 2; i ++){if(a[i] == 0){continue;}else if(a[i] < 0){cout << "NO\n";return ;}else{int tmp = a[i];a[i] -= tmp;a[i + 1] -= 2 * tmp;a[i + 2] -= tmp;}}if(a[n] == 0 && a[n - 1] == 0){cout << "YES\n";}else{cout << "NO\n";}
}
Divisible Pairs
这题主要考察对取模的理解
a + b a+b a+b mod x = 0, 即 a + b = p ∗ x a+b=p*x a+b=p∗x , 所有数对 x x x 取模,a%=x,b%=x , 得 a + b = 0 o r x a+b=0\;or\;x a+b=0orx
a − b a-b a−b mod x = 0, 取模 x, 即 a=b
一边读入一边计算,不会重复计算
void solve(){int n, x, y, res = 0;cin >> n >> x >> y;map<pair<int, int>, int> mp;for(int i = 1; i <= n; i ++){int tmp;cin >> tmp;if(mp.count({x - tmp % x, tmp % y})){res += mp[{x - tmp % x, tmp % y}];}else if(mp.count({-tmp % x, tmp % y})){res += mp[{-tmp % x, tmp % y}];}mp[{tmp % x, tmp % y}] ++;}cout << res << '\n';
}
Anna and the Valentine’s Day Gift
如果 x ≥ 1 0 m x\geq 10^m x≥10m , 在 x x x 没有前导零的情况下, 只需要 x x x 的长度为 m + 1 m+1 m+1 即可,知道这个性质贪心两边操作即可
(萨沙不需要最大化最终的数字,只要最大化数字的位数即可。)
void solve(){int n, m, res = 0;cin >> n >> m;vector<int> a(n + 5), c(n + 5);for(int i = 1; i <= n; i ++){cin >> a[i];res += to_string(a[i]).size();}auto check = [](int x) -> int{string tmp = to_string(x);int sz = tmp.size(), i = sz - 1;while(tmp[i] == '0') i --;return sz - i - 1;};sort(a.begin() + 1, a.begin() + n + 1, [&](int x, int y) -> bool{return check(x) > check(y);});for(int i = 1; i <= n; i += 2){res -= check(a[i]);}cout << (res >= m + 1 ? "Sasha" : "Anna") << '\n';
}
Physical Education Lesson
如果位置 n n n 的人报数为 x x x , 队伍长为 k k k , 不难发现
n = ( 2 k − 2 ) ∗ t + x n=(2k-2)*t+x n=(2k−2)∗t+x , t ∈ [ 0 , ⌊ n − x 2 k − 2 ⌋ ] t\in[0,\lfloor\frac{n-x}{2k-2}\rfloor] t∈[0,⌊2k−2n−x⌋]
或 n = ( 2 k − 2 ) ∗ t + k + k − x n=(2k-2)*t+k+k-x n=(2k−2)∗t+k+k−x , 即 t ∈ [ 1 , 1 + ⌊ n + x − 2 2 k − 2 ⌋ ] t\in[1,1+\lfloor\frac{n+x-2}{2k-2}\rfloor] t∈[1,1+⌊2k−2n+x−2⌋]
对 n − x n-x n−x 和 n + x − 2 n+x-2 n+x−2 分解因子,留下偶数因子对应的 k k k 插入 s e t set set 集合当中,
最后检查所有 k > = x k>=x k>=x 的合法解数量
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n, x;
void solve(){set<int> s;cin >> n >> x;/*n = (2k-2)*t + xn-x = (2k-2)*tn = (2k-2)*t + k + k - xn + x - 2 = (2k-2) * tk < n*//*num = a * b*/auto op = [&](int num){set<int> tmp = set<int> ();for(int i = 1; i * i <= num; i ++){if(num % i == 0){if(i % 2 == 0) tmp.insert(i);if((num / i) % 2 == 0) tmp.insert(num / i);}}for(auto x : tmp){s.insert(x / 2 + 1);}};op(n - x);op(n + x - 2);int res = 0;for(auto k : s){if(k >= x){res ++;}}cout << res << '\n';
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int T = 1;cin >> T;while (T --){solve();}return 0;
}
/*10 22356n-x=8, 2 4 8 2 3 5n+x-2=10 2 10
*/
Eat the chip
纵向距离决定谁吃谁,然后进行模拟,被吃者逃离,捕食者靠近, O ( h ) O(h) O(h)
实际存在 O ( 1 ) O(1) O(1) 做法就能判断,这里不做深究
#include<bits/stdc++.h>
using namespace std;
#define int long long// void solve(){
// int h, w, x1, y1, x2, y2;
// cin >> h >> w >> x1 >> y1 >> x2 >> y2;
// auto out = [](int op){
// if(op == 1) cout << "Alice\n";
// else if(op == 2) cout << "Bob\n";
// else cout << "Draw\n";// };// if(x1 >= x2){// out(3);// }
// else{
// int dis = abs(y1 - y2);
// if(dis <= 1){
// if(abs(x1 - x2) % 2){
// out(1);
// }
// else{
// out(2);
// }
// }
// else{
// out(3);
// }
// }
// }
/*获胜条件 : 当被捕食者进入攻击区域时,捕食者通过之前的操纵使得两者距离之差不超过 3除非距离间隔为 1, 捕食者直接发起进攻否则被捕食者一定
*/
/*如果两者距离为 0, 捕食者不改变, 否则,捕食者令距离减 -1;被捕食者一定要让距离 + 1捕食者先手, 而被捕食者进入判定区域时先手假设横向距离为 3,纵向距离为 51 : 22 : 33 : 24 : 3h <= 1e6即纵向的距离, 显然题目比较善良,让我们通过 O(h) 而非 O(1)的操作完成题目那么就可以通过模拟解决了
*/
void solve(){int h, w, x1, y1, x2, y2;cin >> h >> w >> x1 >> y1 >> x2 >> y2;auto out = [](int op){if(op == 1) cout << "Alice\n";else if(op == 2) cout << "Bob\n";else cout << "Draw\n";};// 计算横向距离auto dis = [&] () -> long long {return abs(y1 - y2);};// a 远离 bauto a_away_b = [&] () -> void {for(int i = -1; i <= 1; i ++){int tmp = y1 + i;if(tmp >= 1 && tmp <= w && abs(tmp - y2) >= dis()){y1 = tmp;}}};auto a_in_b = [&] () -> void {for(int i = -1; i <= 1; i ++){int tmp = y1 + i;if(tmp >= 1 && tmp <= w && abs(tmp - y2) <= dis()){y1 = tmp;}}};auto b_away_a = [&] () -> void {for(int i = -1; i <= 1; i ++){int tmp = y2 + i;if(tmp >= 1 && tmp <= w && abs(tmp - y1) >= dis()){y2 = tmp;}}};auto b_in_a = [&] () -> void {for(int i = -1; i <= 1; i ++){int tmp = y2 + i;if(tmp >= 1 && tmp <= w && abs(tmp - y1) <= dis()){y2 = tmp;}}};if(x1 >= x2){out(3);}else{// 进入判定区域的时候,结局就已经注定了if((x2 - x1) % 2 == 1){ // A 吃 Bfor(int i = 1; i <= x2 - x1 - 1; i ++){if(i & 1){a_in_b();}else{b_away_a();}}if(abs(y1 - y2) <= 1) out(1);else out(3);}else{ // B 吃 Afor(int i = 1; i <= x2 - x1 - 1; i ++){if(i & 1){a_away_b();}else{b_in_a();}}if(abs(y1 - y2) <= 1) out(2);else out(3);}}}
signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int T = 1;cin >> T;while (T --){solve();}return 0;
}
// 每次移动改变两棋子之间的横向距离 dis_x 和纵向距离 dis_y
// 先手到达 dis_x = 0 且 dis_y = 0 的玩家获胜
// 如果无人取胜,平局。
// 每次操作,纵向距离必然 -1
// 如果两者距离为奇数, 必然是 A 尝试吃掉 B 或者平局
// 如果两者距离为偶数,必然是 B 尝试吃掉 A 或者平局
Increasing Subsequences
题解写的很好
让我们来看看构建所需数组的解决方案之一。
假设数组 a a a 有 x x x 个递增子序列。如果我们在数组末尾添加一个新的最小值,那么新数组中的递增子序列数等于 x + 1 x+1 x+1 (因为新元素不会与其他元素形成递增子序列)。(由于新元素不会与其他元素形成递增子序列,因此只会添加由该元素组成的子序列)。如果我们在数组的末尾添加一个新的最大值,那么新数组中的递增子序列数等于 2 x 2x 2x (因为新元素与其他元素形成递增子序列)。
利用上述事实,我们来定义一个递归函数 f ( x ) f(x) f(x) ,它返回的数组恰好有 x x x 个递增子序列。对于奇数值 x x x ,返回 f ( x ) = f ( x − 1 ) + m i n f(x) = f(x-1) + min f(x)=f(x−1)+min (这里的 + 表示在数组末尾添加一个元素);对于偶数值 x x x ,返回 f ( x ) = f ( x 2 ) + m a x f(x) = f(\frac{x}{2}) + max f(x)=f(2x)+max 。现在我们需要估算通过这种算法得到的数组中的元素个数。需要注意的是,第一种类型( x → x − 1 x \rightarrow x-1 x→x−1 )不能有两次连续的运算,因此每两次运算, x x x 的值至少减少两次。因此,数组的大小满足 200 200 200 的限制。
#include<bits/stdc++.h>
using namespace std;
#define int long longvector<int> f(int x){vector<int> res;if(x == 2){res.push_back(0);}else if(x & 1){res = f(x - 1);res.push_back(*min_element(res.begin(), res.end()) - 1);}else{res = f(x / 2);res.push_back(*max_element(res.begin(), res.end()) + 1);}return res;
}void solve(){int x;cin >> x;auto res = f(x);cout << res.size() << '\n';for(auto a : res) cout << a << ' ';cout << '\n';
}signed main(){ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int T = 1;cin >> T;while (T --){solve();}return 0;
}
相关文章:

Mashup-Math_Topic_One
Tutorial and Introspection A Rudolf and 121 注意到第 1 1 1 位只能被第 2 2 2 位影响,以此类推位置,对于 a i a_i ai , 如果 < 0 < 0 <0 ,不合法 ; 否则, a i − a i , a i 1 − 2 ∗ a i , a i 2 − a …...
基于JavaWEB SSM SpringBoot婚纱影楼摄影预约网站设计和实现
基于JavaWEB SSM SpringBoot婚纱影楼摄影预约网站设计和实现 博主介绍:多年java开发经验,专注Java开发、定制、远程、文档编写指导等,csdn特邀作者、专注于Java技术领域 作者主页 央顺技术团队 Java毕设项目精品实战案例《1000套》 欢迎点赞 收藏 ⭐留言…...
逐步学习Go-Select多路复用
概述 这里又有多路复用,但是Go中的这个多路复用不同于网络中的多路复用。在Go里,select用于同时等待多个通信操作(即多个channel的发送或接收操作)。Go中的channel可以参考我的文章:逐步学习Go-并发通道chan(channel)…...

王道:OJ15
课时15作业 Description 读取10个元素 87 7 60 80 59 34 86 99 21 3,然后建立二叉查找树,排序后输出3 7 21 34 59 60 80 86 87 99,针对有序后的元素,存入一个长度为10的数组中,通过折半查找找到21的下标(…...
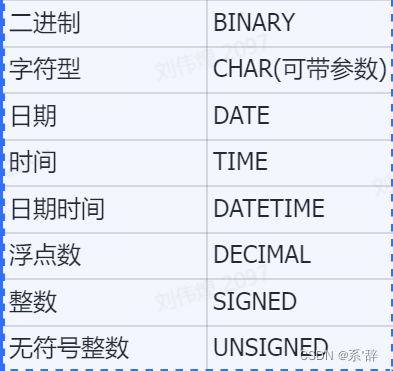
【案例·查】数据类型强制转换,方便查询匹配
问题描述: MySQL执行中需要将某种数据类型的表达式显式转换为另一种数据类型,可以使用 SQL 中的cast()来处理 案例: SELECT CAST(9.0 AS decimal) #String化为小数类型SELECT * FROM table_1 WHERE 1888-03-07 CAST(theDate AS DATE) …...
spring boot3自定义注解+拦截器+Redis实现高并发接口限流
⛰️个人主页: 蒾酒 🔥系列专栏:《spring boot实战》 🌊山高路远,行路漫漫,终有归途 目录 写在前面 内容简介 实现思路 实现步骤 1.自定义限流注解 2.编写限流拦截器 3.注册拦截器 4.接口限流测试 写在前…...
使用certbot为网站启用https
1. 安装certbot客户端 cd /usr/local/bin wget https://dl.eff.org/certbot-auto chmod ax ./certbot-auto 2. 创建目录和配置nginx用于验证域名 mkdir -p /data/www/letsencryptserver {listen 80;server_name ~^(?<subdomain>.).ninvfeng.com;location /.well-known…...

Unity 背包系统中拖拽物体到指定位置或互换位置效果的实现
在Unity中,背包系统是一种常见的游戏系统,可以用于管理和展示玩家所持有的物品、道具或装备。 其中的拖拽功能非常有意思,具体功能就是玩家可以通过拖拽物品图标来移动物品在背包中的位置,或者将物品拖拽到其他位置或界面中&…...
iOS客户端自动化UI自动化airtest+appium从0到1搭建macos+脚本设计demo演示+全网最全最详细保姆级有步骤有图
Android客户端自动化UI自动化airtest从0到1搭建macos脚本设计demo演示全网最全最详细保姆级有步骤有图-CSDN博客 避坑系列-必读: 不要安装iOS-Tagent ,安装appium -这2个性质其实是差不多的都是为了安装wda。注意安装appium最新版本,安装完…...

每周编辑精选|在线运行 Deepmoney 金融大模型、AI 偏好等多个优质数据集上线
目前,AI 领域对金融模型的研究成果大多是基于公共知识进行训练的,但在实际的金融实践中,这些公共知识对于当前市场的可解释性往往严重不足。一个理想的金融大模型应该能够理解新闻或数据事件,并能够即时地从主观和量化两个角度对事…...
C++多重继承与虚继承
多重继承的原理 多重继承(multiple inheritance)是指从多个直接基类中产生派生类的能力。 多重继承的派生类继承了所有父类的属性。 在面向对象的编程中,多重继承意味着一个类可以从多个父类继承属性和方法。 就像你有一杯混合果汁,它是由多种水果榨取…...

请简单介绍一下Shiro框架是什么?Shiro在Java安全领域的主要作用是什么?Shiro主要提供了哪些安全功能?
请简单介绍一下Shiro框架是什么? Shiro框架是一个强大且灵活的开源安全框架,为Java应用程序提供了全面的安全解决方案。它主要用于身份验证、授权、加密和会话管理等功能,可以轻松地集成到任何Java Web应用程序中,并提供了易于理解…...

TouchGFX之Button
TouchGFX中的按钮是一种感应触控事件的控件,能够在按钮被按下/释放时发送回调 代码 #ifndef TOUCHGFX_ABSTRACTBUTTON_HPP #define TOUCHGFX_ABSTRACTBUTTON_HPP #include <touchgfx/Callback.hpp> #include <touchgfx/events/ClickEvent.hpp> #includ…...
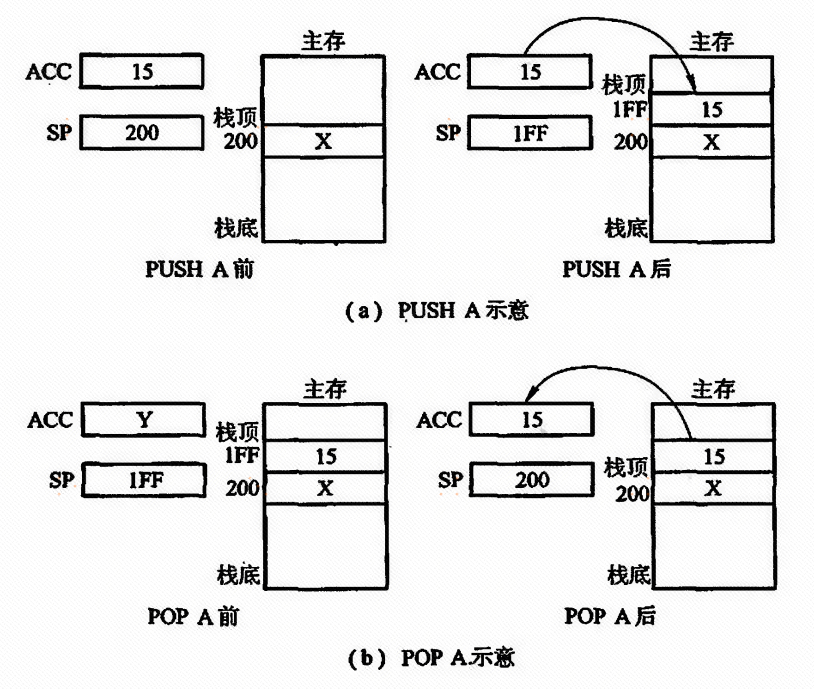
计算机组成原理 — 指令系统
指令系统 指令系统指令的概述指令的格式指令的字长取决于 操作数类型和操作种类操作数的类型数据在存储器中的存放方式操作类型 寻址方式指令寻址数据寻址立即寻址直接寻址隐含寻址间接寻址寄存器寻址寄存器间接寻址基址寻址变址寻址堆栈寻址 RISC 和 CISC 技术RISC 即精简指令…...

使用easyYapi生成文档
easyYapi生成文档 背景1.安装配置1.1 介绍1.2 安装1.3 配置1.3.1 Export Postman1.3.2 Export Yapi1.3.3 Export Markdown1.3.4 Export Api1.3.6 常见问题补充 2. java注释规范2.1 接口注释规范2.2 出入参注释规范 3. 特定化支持3.1 必填校验3.2 忽略导出3.3 返回不一致3.4 设置…...

蓝桥杯练习题总结(三)线性dp题(摆花、数字三角形加强版)
目录 一、摆花 思路一: 确定状态: 初始化: 思路二: 确定状态: 初始化: 循环遍历: 状态转移方程: 二、数字三角形加强版 一、摆花 题目描述 小明的花店新开张,为了吸…...
 multi_match的使用)
Elasticsearch(15) multi_match的使用
elasticsearch version: 7.10.1 multi_match是Elasticsearch中的一种查询类型,允许在一个或多个字段上执行全文本搜索,并合并各个字段的结果得分。这种查询有助于实现跨多个字段的统一搜索体验。 语法 {"query": {"multi_m…...

nodejs的线程模型和libuv库的基本使用
文章目录 nodejs中集成addon本地代码的回调问题单线程事件驱动模型libuvlibuv基本框架addon中使用libuv代码nodejs中集成addon本地代码的回调问题 在C++的代码中,回调函数是一个基本的代码调用方式。而在我自己的开发实践中,需要在addon这样一个nodejs的本地化模块中实现一个…...
Uni-app/Vue/Js本地模糊查询,匹配所有字段includes和some方法结合使用e
天梦星服务平台 (tmxkj.top)https://tmxkj.top/#/ 1.第一步 需要一个数组数据 {"week": "全部","hOutName": null,"weekendPrice": null,"channel": "门市价","hOutId": 98,"cTime": "…...
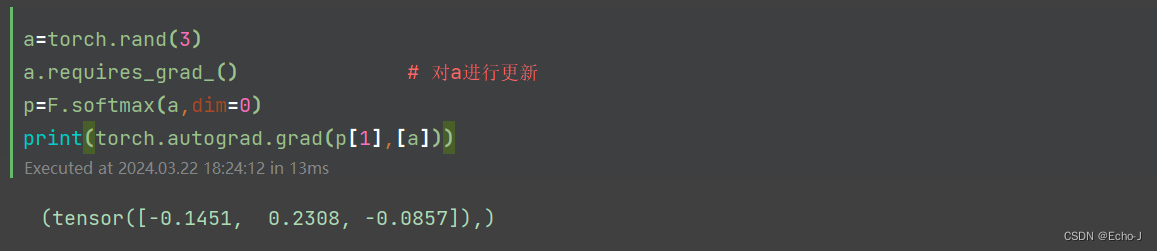
深度学习pytorch——激活函数损失函数(持续更新)
论生物神经元与神经网络中的神经元联系——为什么使用激活函数? 我们将生物体中的神经元与神经网络中的神经元共同分析。从下图可以看出神经网络中的神经元与生物体中的神经元有很多相似之处,由于只有刺激达到一定的程度人体才可以感受到刺激,…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
