深度学习pytorch——激活函数损失函数(持续更新)
论生物神经元与神经网络中的神经元联系——为什么使用激活函数?
我们将生物体中的神经元与神经网络中的神经元共同分析。从下图可以看出神经网络中的神经元与生物体中的神经元有很多相似之处,由于只有刺激达到一定的程度人体才可以感受到刺激,并且人体对刺激做出的响应是有限的,所以在输出之前应该经过激活函数。这个激活函数可以将原来发散的数据变成收敛的数据。

什么是梯度?
函数在某一点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
接下来我们将研究激活函数的梯度问题,我们将从代码实践中,获得明确的结果,更清楚激活函数的作用。
激活函数及其梯度
我们如果使用如下函数,会发现在0点函数是不可导的,我们找到一个近似此函数的分布的可导函数。

1、Sigmoid/Logistic
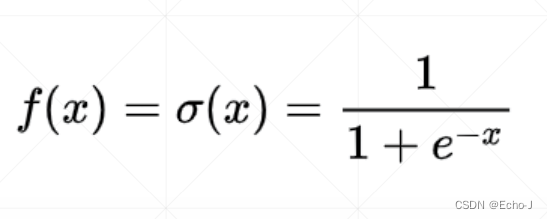
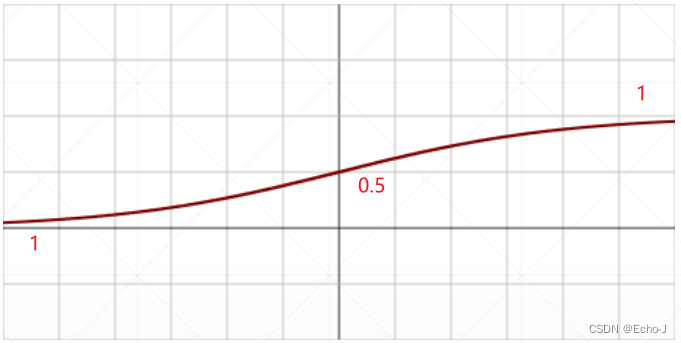
sigmoid函数的取值范围为[0, 1],因此可以使用sigmoid函数可以对数据进行压缩。
注意:由于sigmoid函数随着x的增大会逐渐趋近于1,此时sigmod的导数,就是趋近于0,就是梯度为0,在对参数进行更新的过程中我们会使用到梯度,新参数=旧参数-学习率*梯度,这就会导致参数长时间得不到更新,造成梯度离散的情况。
对sigmoid函数求导,可以得到![]() 。由于激活函数在神经网络中是已知的,因此sigmoid函数的导数也是已知的,这非常有利于我们的计算。
。由于激活函数在神经网络中是已知的,因此sigmoid函数的导数也是已知的,这非常有利于我们的计算。
代码演示:
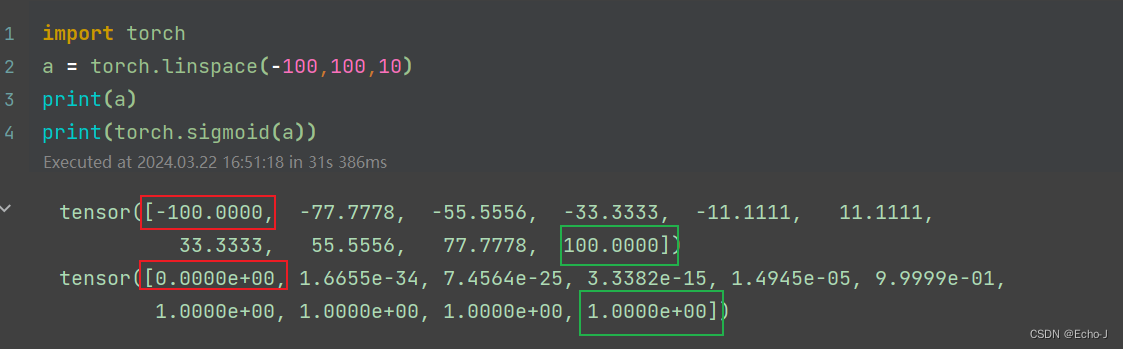
我们从代码情况中可以明显看到,经过sigmoid 函数之后所有的值都在0-1范围内,sigmoid函数的确对数据起到了一个压缩效果。
这里的torch.sigmoid()也可以使用F.sigmoid(),其中F来自于torch.nn.functional as F。
2、Tanh

对Tanh函数进行求导,得到:
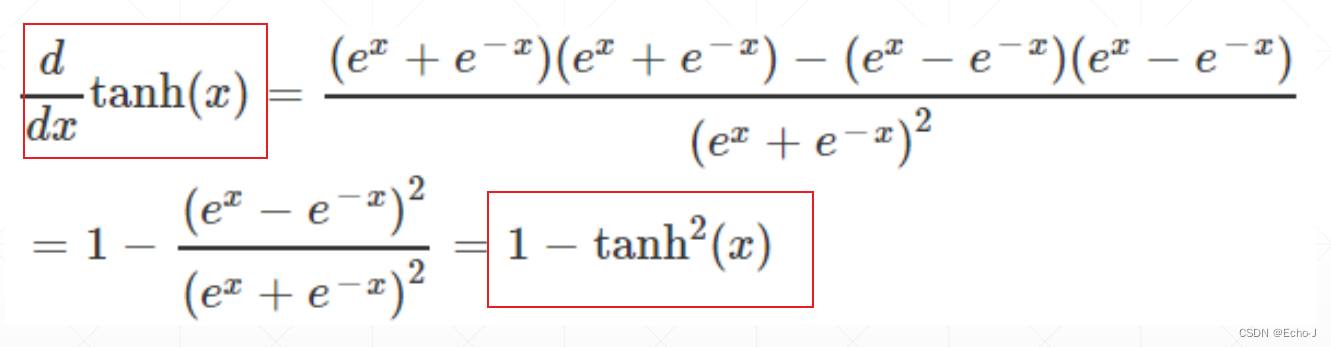
代码演示:
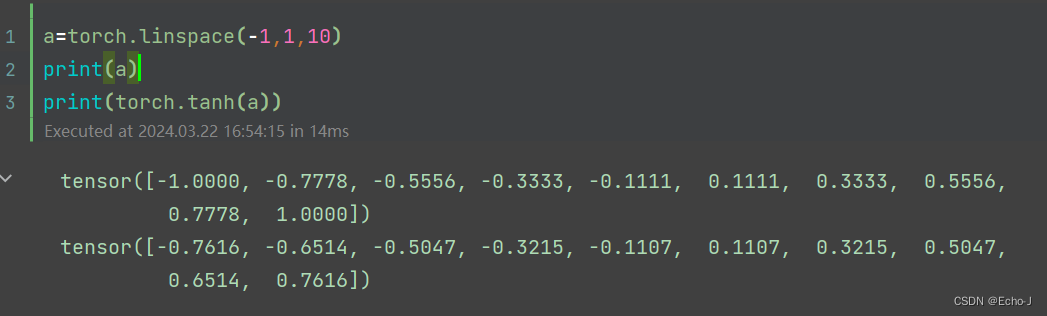
应用:RNN
3、ReLU

ReLU激活函数是我们使用最多的,因为它再一定程度上解决了梯度离散的问题,并且它的导数非常的简单,在小于0时,为0;在大于0时,为1。相对于Sigmoid激活函数,在一定情况下解决了梯度离散的情况,在现实中,它表现出来的深度学习效果也是非常好的。
对ReLU函数进行求导:

代码演示:

最后的结果,小于零的数值都取值为0,大于零的不改变。但是这个函数怎么对数据进行压缩锕?我们可以通过多个ReLU函数进行叠加,具体可以参考机器学习笔记(持续更新)-CSDN博客,ReLU函数在最后。
4、Leaky ReLU
ReLU函数再x <= 0时,导数为0,会出现梯度离散的情况,Leaky ReLU函数很好的解决了这一问题。

并且使用非常简单,直接调用LeakyReLU()函数即可,并且可以通过属性指定x <= 0时的倾斜角度,代码示例:

5、SELU
为了解决ReLU函数在x = 0时是不可导的,引入了SELU函数,这个函数是由ReLU函数和一个指数函数组合而成。

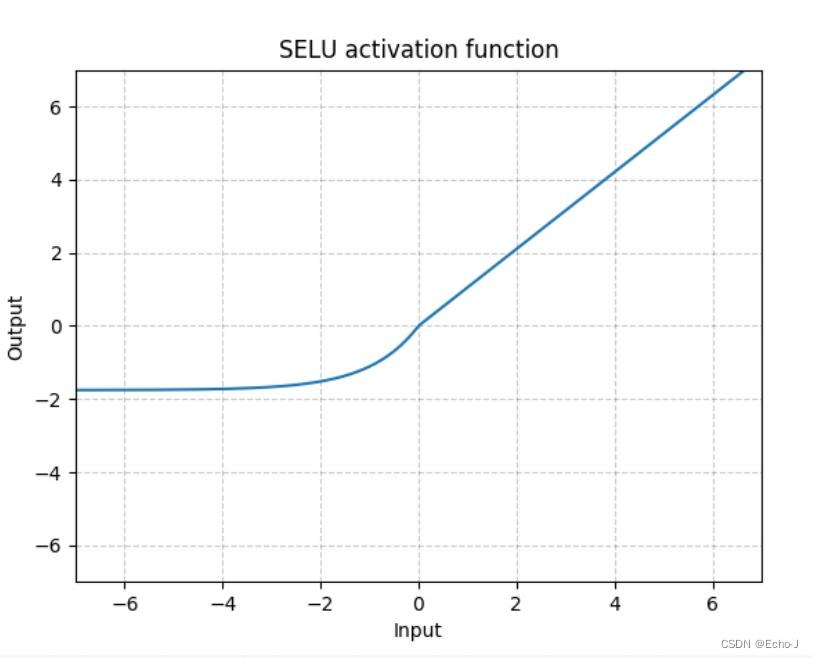
6、softplus
softplus函数在0点左右的切线正好交与原点。

Loss及其梯度
损失函数主要分为均方差损失(Mean Squared Error)、交叉熵损失(Cross Entropy Loss)。
1、MSE(Mean Squared Error)
我们使用一个线性感知机问题讨论MSE。我们来看两种损失函数计算的方式:


将模型(预测值模型)推广到任意模型,将参数统称为,对损失函数进行求导。

注意:在对w求梯度之前一定要记得对参数进行更新
(1)利用autograd.grad()求梯度:

不对w进行更新会报错element 0 of tensors does not require grad and does not have a grad_fn
蓝色标记的话就是答案,意思就是将每次的损失添加到总损失中,可以通过添加 requires_grad=True解决问题。以上代码也可以这样写,直接在w初始化时,加入requires_grad=True。

(2)利用backward()求梯度:

2、Cross Entropy Loss
交叉熵损失可以用于二分类问题、多分类问题、逻辑回归。通常使用softmax函数作为激活函数。
softmax函数:
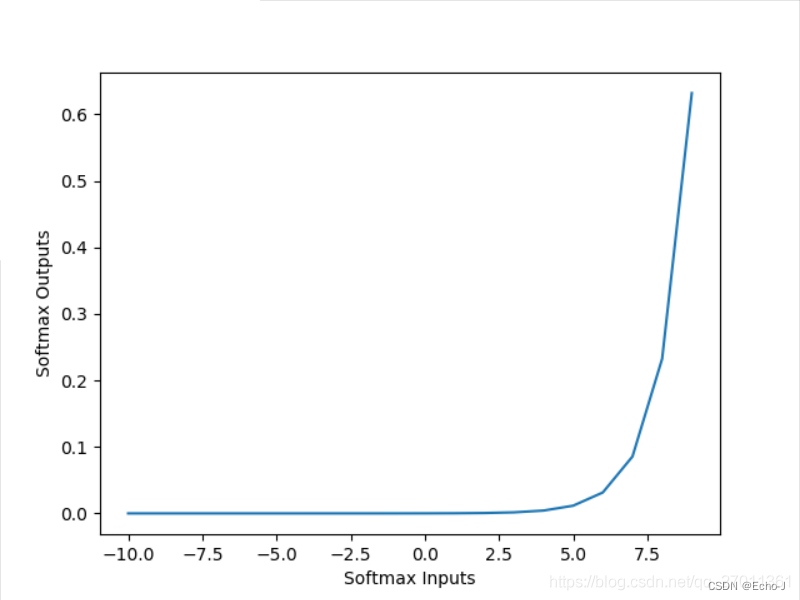

这个激活函数经常用来处理分类问题。如上图,我们对这个函数输入2、1、0.1这几个数,经过softmax函数,输出的结果为0.7、0.2、0.1范围都在0-1之间,并且总和为1。而且这个函数还起到强化的作用,在输入方2:1=2,在输出方0.7:0.2=3.5,比原来强的更强、弱的更弱。
对于此函数的导数:
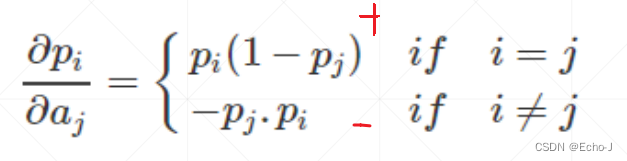
在 i = j 的时候大于0,在 i != j 的时候小于0。
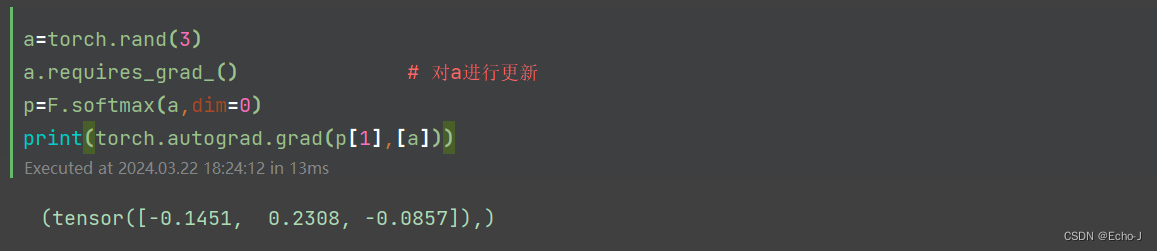
代码演示:
a=torch.rand(3)
a.requires_grad_() # 对a进行更新
p=F.softmax(a,dim=0)
print(p)
print(torch.autograd.grad(p[1],[a],retain_graph=True))
print(torch.autograd.grad(p[2],[a])) 为什么需要添加retain_graph=True?我想以下的回答将会为你解答:

大意就是retain_graph=True不会释放被保存的张量(不会释放中间体),而这些张量在以后计算梯度时将会被用到。导致的结果就是使用backward来计算梯度的次数不能超过一次。
我尝试了多次使用了backward来计算梯度,得到:RuntimeError: Trying to backward through the graph a second time (or directly access saved tensors after they have already been freed). Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved tensors after calling backward.
代码演示:
第一次测试
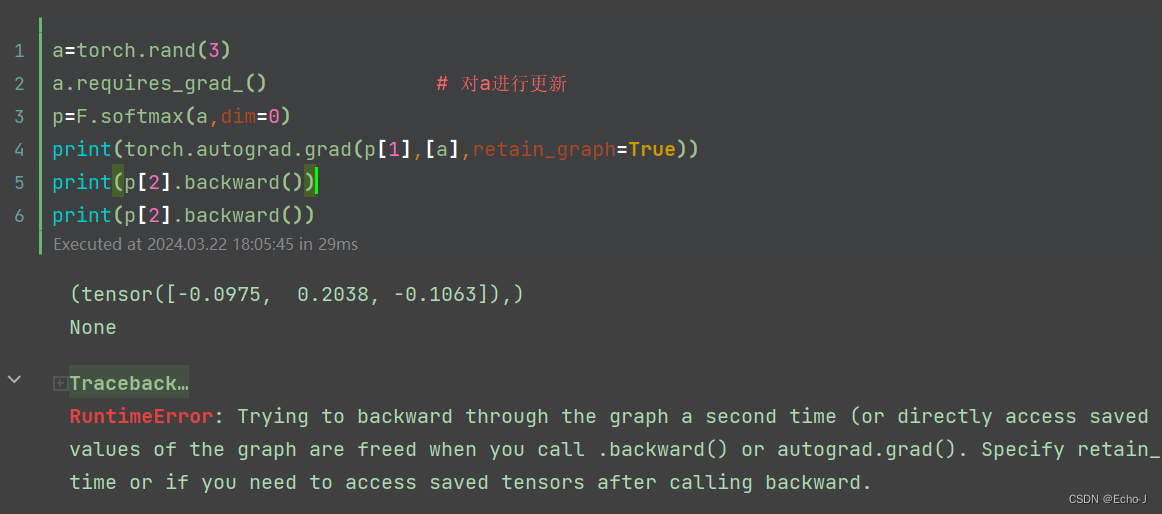
第2次测试:
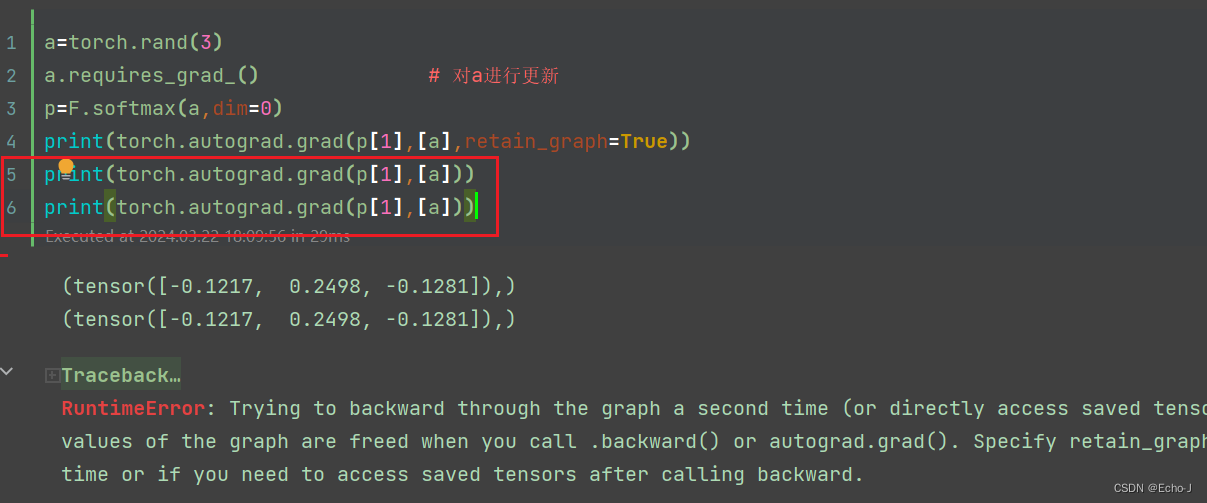
第3次测试:

第4次测试:
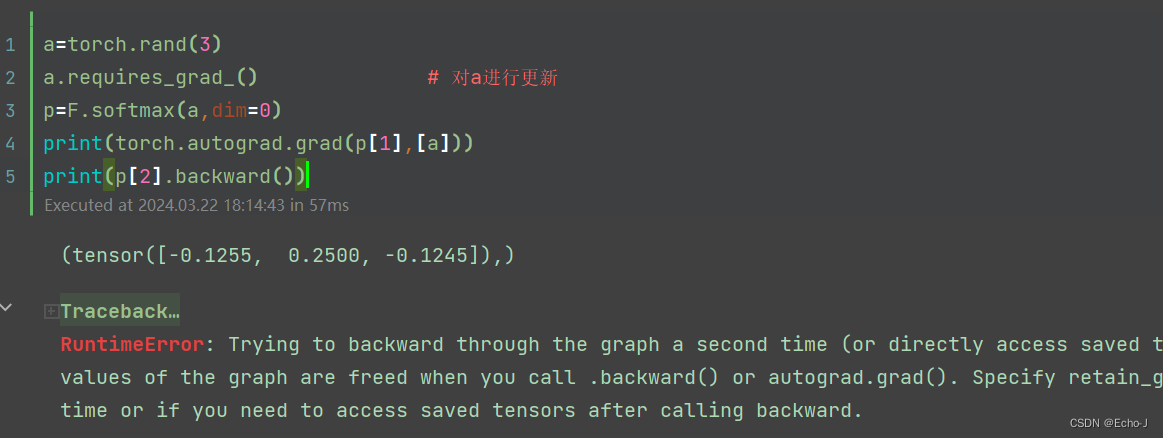 经过多次测验,我发现上面的回答是不是有问题?因此我又找了一个:
经过多次测验,我发现上面的回答是不是有问题?因此我又找了一个:
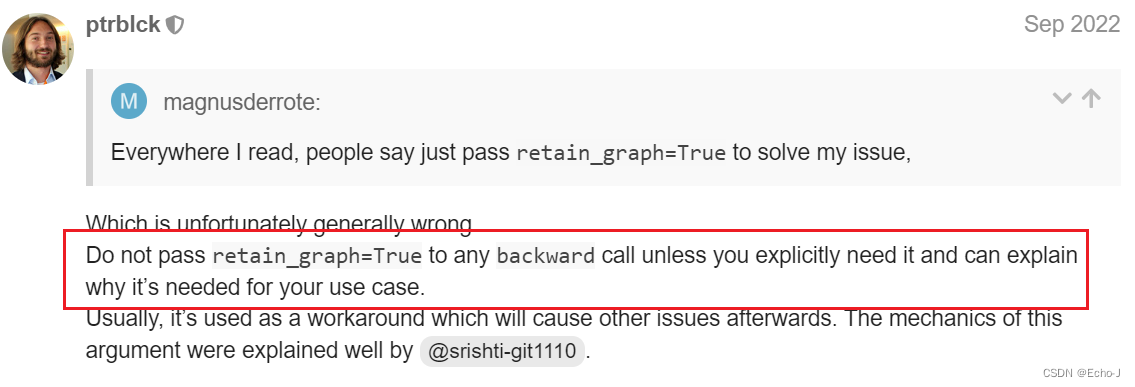
大意就是retain_graph=True非必要不使用。
因此最后的代码应该是:
如果以上内容有什么问题,欢迎指正,I would be grateful。
相关文章:

深度学习pytorch——激活函数损失函数(持续更新)
论生物神经元与神经网络中的神经元联系——为什么使用激活函数? 我们将生物体中的神经元与神经网络中的神经元共同分析。从下图可以看出神经网络中的神经元与生物体中的神经元有很多相似之处,由于只有刺激达到一定的程度人体才可以感受到刺激,…...

《苹果 iOS 应用开发与分发的关键问题解析》
一、背景 解决同事问的问题,来来回回被问好几次相同的问题,然后确认,我觉得不如写个文档 二、非研发人员安装iOS应用方式 TestFlightIPA 文件 对比 TestFlightIPA 文件安装方式TestFlight 是苹果提供的一个 beta 测试平台,开发者…...

爱上数据结构:顺序表和链表
一、线性表 线性表(linear list)是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使 用的数据结构,常见的线性表:顺序表、链表、栈、队列、字符串... 线性表在逻辑上是线性结构,也就说是连续的一条…...

python知识点总结(十)
python知识点总结十 1、装饰器的理解、并实现一个计时器记录执行性能,并且将执行结果写入日志文件中2、队列和栈的区别,并且用python实现3、设计实现遍历目录与子目录4、CPU处理进程最慢的情况通常发生在以下几种情况下:5、CPU处理线程最慢的…...

【Python】探索 Python 编程世界:常量、变量及数据类型解析
欢迎来CILMY23的博客 本篇主题为 探索 Python 编程世界:常量、变量及数据类型解析 个人主页:CILMY23-CSDN博客 Python系列专栏:http://t.csdnimg.cn/HqYo8 上一篇博客: http://t.csdnimg.cn/SEdbp C语言专栏: htt…...

vue页面实现左右div宽度,上下div高度分割线手动拖动高度或者宽度自动变化,两个div宽度或者高度拉伸调节,实现左右可拖动改变宽度的div内容显示区
实现左右或者上下div两部分拖动,宽度或者高度自动变化,实现流畅平滑的变化,还可以是实现拖动到一定宽度就不让拖动了,如果你不需要最小宽度,就直接去掉样式就行 这是页面。分左中右三部分,中间我是用来作为拖动的按钮…...

知攻善防应急靶场-Linux(1)
前言: 堕落了三个月,现在因为被找实习而困扰,着实自己能力不足,从今天开始 每天沉淀一点点 ,准备秋招 加油 注意: 本文章参考qax的网络安全应急响应和知攻善防实验室靶场,记录自己的学习过程&am…...

ffmpeg命令行
ffmpeg 如果要在linux gdb 调试,需要在configure 时候不优化 开启调试 ./configure --enable-debug --disable-optimizations make如何开启gdb 调试 gdb ffmpeg_gset args -i test.hevc -c:v copy -c:a copy output_265.mp4rh264 的流生成mp4 文件,不转…...
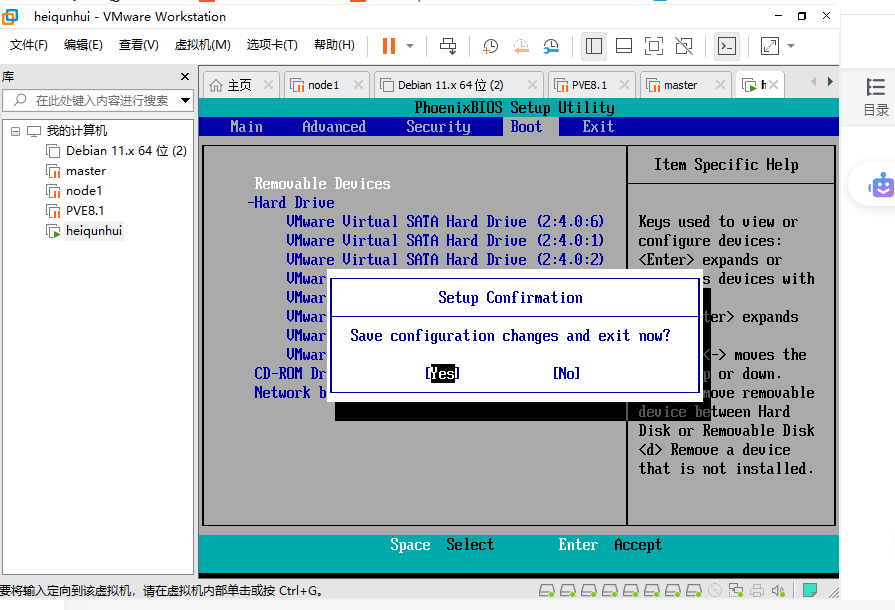
VMware虚拟机更换引导顺序
前言 我用wmware装了黑群晖测试,将img转成vmdisk的格式之后发现系统引导盘之后1G,有点太小了 我准备把wmware的黑群晖系统迁移到新添加的虚拟磁盘里 1.登录黑群晖的SSH 请先在黑群晖的控制面板中的终端机和SNMP里面启用SSH功能,才能使用ss…...
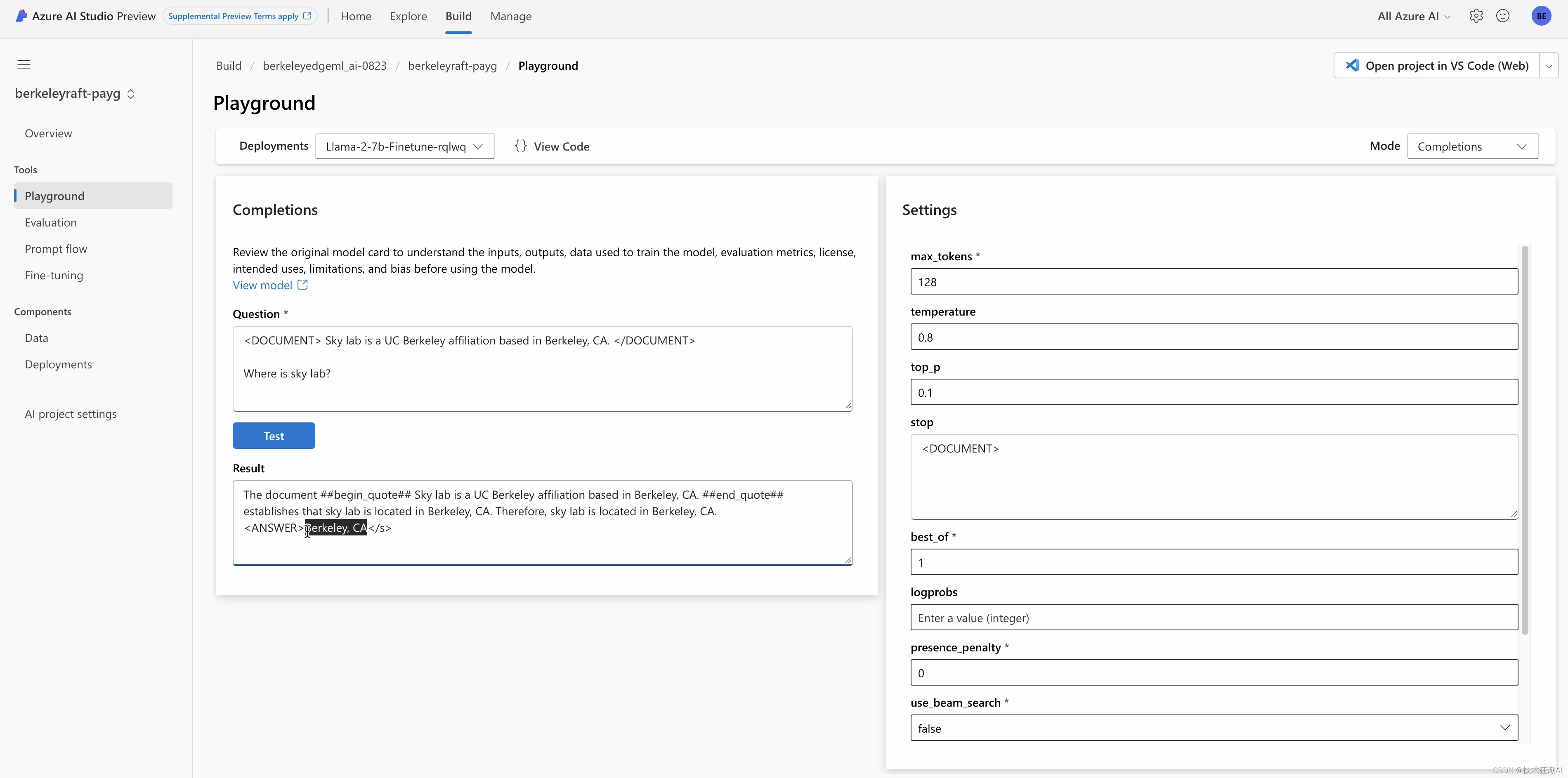
RAFT:让大型语言模型更擅长特定领域的 RAG 任务
RAFT(检索增强的微调)代表了一种全新的训练大语言模型(LLMs)以提升其在检索增强生成(RAG)任务上表现的方法。“检索增强的微调”技术融合了检索增强生成和微调的优点,目标是更好地适应各个特定领…...

Stable Diffusion 本地训练端口与云端训练端口冲突解决办法
方法之一,修改本地训练所用的端口 1 首先,进入脚本训练器的根目录 例如:C:\MarkDeng\lora-scripts-v1.7.3 找到gui.py 2 修改端口号 因为云端训练器也是占用28000和6006端口 那么本地改成27999和6007也是可以的 保存退出,运行启动…...

C++学习day1
思维导图 定义自己的命名空间,其中有string类型的变量,再定义两个函数,一个函数完成字符串的输入,一个函数完成求字符串长度,再定义一个全局函数完成对该字符串的反转 #include <iostream> using namespace std;…...

openGauss CM
CM 可获得性 本特性自openGauss 3.0.0版本开始引入。 特性简介 CM(Cluster Manager)是一款数据库管理软件,由cm_server和cm_agent组成。 cm_agent是部署在数据库每个主机上,用来启停和监控各个数据库实例进程的数据库管理组件…...
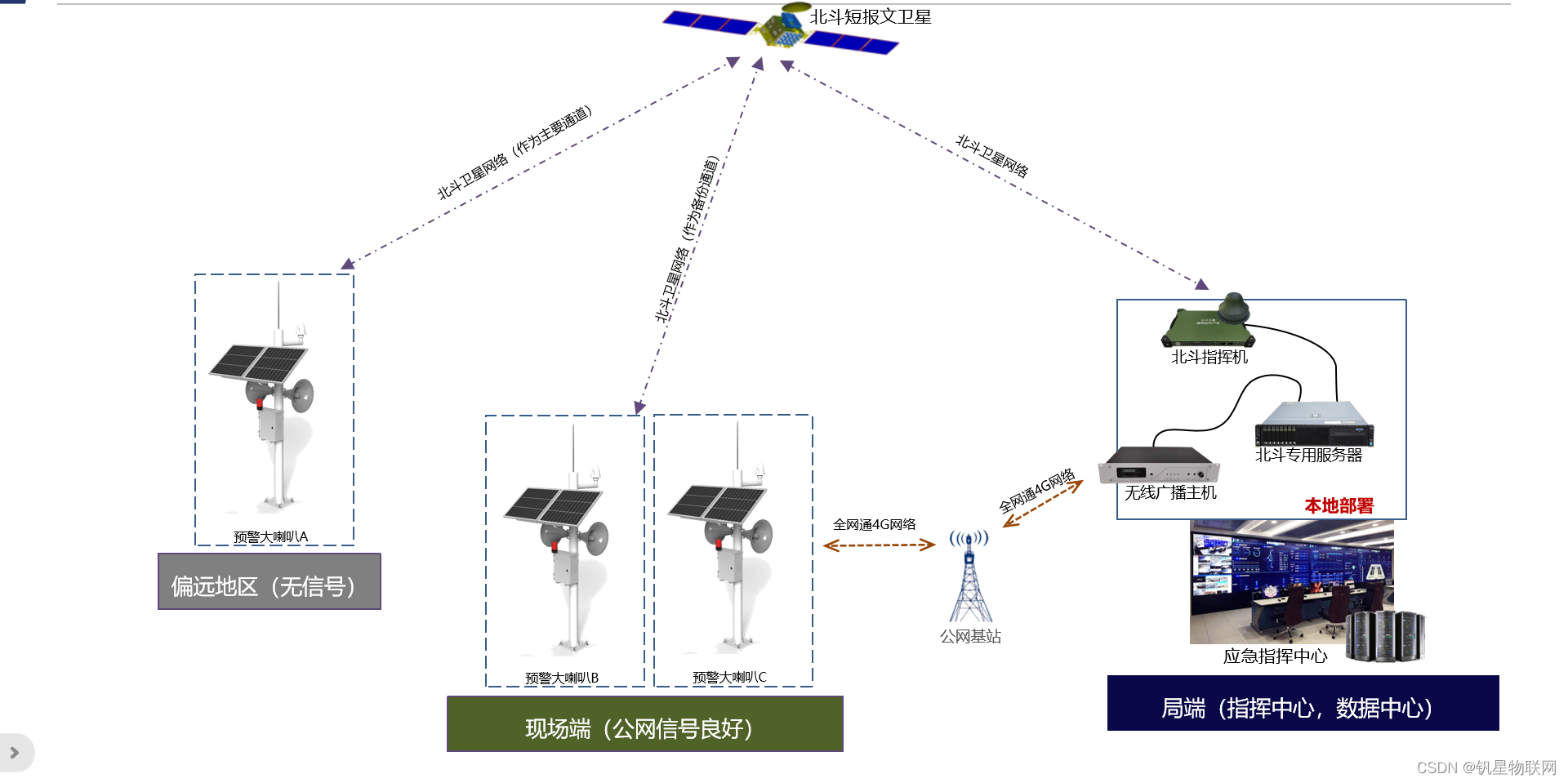
北斗短报文+4G应急广播系统:实时监控 自动预警 保护校园安全的新力量
安全无小事,生命重如山。学生是祖国的未来,校园安全是全社会安全工作的一个重要的组成部分。它直接关系到青少年学生能否安健康地成长,关系到千千万万个家庭的幸福安宁和社会稳定。 灾害事故和突发事件频频发生,给学生、教职员工…...

2024河北石家庄矿业矿山展览会|河北智慧矿山展会|河北矿博会
2024中国(石家庄)国际矿业博览会 时间:2024年7月4-6日 地点:石家庄国际会展中心.正定 随着全球经济的持续增长和矿产资源需求的不断攀升,矿业行业正迎来前所未有的发展机遇。作为矿业领域的盛会&…...

ruoyi使用笔记
1.限流处理 RateLimiter PostMapping("/createOrder") ApiOperation("创建充值订单") RateLimiter(key CacheConstants.REPEAT_SUBMIT_KEY,time 10,count 1,limitType LimitType.IP) public R createOrder(RequestBody Form form) {//业务处理return …...

论文《Exploring to Prompt for Vision-Language Models》阅读
论文《Exploring to Prompt for Vision-Language Models》阅读 论文概况论文动机(Intro)MethodologyPreliminaryCoOp[CLASS]位置Context 是否跨 class 共享表示和训练 ExperimentsOverall ComparisonDomain GeneralizationContext Length (M) 和 backbon…...

科普 | Runes 预挖矿概念
作者:Jacky X/推:zxl2102492 关于 Runes 协议的前世今生,可以点击阅读这篇文章 👇 《简述 Runes 协议、发展历程及最新的「公开铭刻」发行机制的拓展讨论》 什么是传统预挖矿概念 这轮比特币生态爆发之前,预挖矿&…...
蓝桥杯真题Day40 倒计时19天 纯练题!
蓝桥杯第十三届省赛真题-统计子矩阵 题目描述 给定一个 N M 的矩阵 A,请你统计有多少个子矩阵 (最小 1 1,最大 N M) 满足子矩阵中所有数的和不超过给定的整数 K? 输入格式 第一行包含三个整数 N, M 和 K. 之后 N 行每行包含 M 个整数…...

Android 14.0 SystemUI下拉状态栏增加响铃功能
1.概述 在14.0的系统产品rom定制化开发中,在对systemui的状态栏开发中,对SystemUI下拉状态栏的QuickQSPanel区域有快捷功能键开关,对于增加各种响铃快捷也是常用功能, 有需要增加响铃功能开关功能,接下来就来分析SystemUI下拉状态栏QuickQSPanel快捷功能键开关的相关源码…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
