蓝桥杯练习题总结(三)线性dp题(摆花、数字三角形加强版)
目录
一、摆花
思路一:
确定状态:
初始化:
思路二:
确定状态:
初始化:
循环遍历:
状态转移方程:
二、数字三角形加强版
一、摆花
题目描述
小明的花店新开张,为了吸引顾客,他想在花店的门口摆上一排花,共m盆。通过调查顾客的喜好,小明列出了顾客最喜欢的n种花,从1到n标号。为了在门口展出更多种花,规定第i种花不能超过αi盆。摆花时同一种花放在一起,且不同种类的花需按标号的从小到大的顺序依次摆列。试编程计算,一共有多少种不同的摆花方案。
输入描述
第一行包含两个正整数n和m,中间用一个空格隔开。
第二行有n个整数,每两个整数之间用一个空格隔开,依次表示a1、a2、...、an。
其中,0 < n ≤ 100,0 < m ≤ 100,0 ≤ ai ≤ 100。
输出描述
输出只有一行,一个整数,表示有多少种方案。注意:因为方案数可能很多,请输出方案数对10^9 + 7取模的结果。
输入样例
2 4 3 2
输出样例
2
解题思路
思路一:
确定状态:
首先,需要明确问题的要求:给定n种不同的花和每种花的最大数量限制,求出在摆放m盆花时,能够形成的不同摆花方案数。这个问题的关键在于每种花可以选择摆放的数量从0到其最大限制,且摆放的花必须按照花的种类顺序排列。

在动态规划中,定义状态是至关重要的一步。这里,我们定义状态dp[i][j]为考虑前i种花时,摆放j盆花的不同方案数。
int n, m; cin >> n >> m;
vector<int>a(n + 1);
vector<vector<int> >dp(101, vector<int>(101));初始化:
初始化第一种花的情况,因为只有一种花,所以可以从0到a[1]朵任意选择,都只有一种方式
for (int i = 0; i <= a[1]; i++) dp[1][i] = 1;-
外层循环遍历花的种类:从1到
n,(花的种类为0时情况已初始化)对每种花进行遍历。 -
中层循环遍历目标花的总数:从0到
m,对可能摆放的花的总数进行遍历。 - 在内层循环中,再加一个循环遍历当前考虑的这种花可以选择的数量(从0到该种花的数量上限或剩余可摆放数量的较小值),这里通过检查
j - k >= 0来确保不会有负数的情况发生。
for (int i = 2; i <= n; i++) { // 遍历每一种花 for (int j = 0; j <= m; j++) { // 遍历当前要选的花的总数for (int k = 0; k <= a[i] && j - k >= 0; k++) {......}}}- 状态转移方程
dp[i][j] = (dp[i][j] + dp[i - 1][j - k]) % p;的含义是,要得到前i种花中摆放j盆花的方案数,需要将所有可能包含第i种花的数量(从0到a[i])的方案数加起来。每次更新dp[i][j]时,都要对p取模,以避免整数溢出并满足题目要求。
dp[i][j] = (dp[i][j] + dp[i - 1][j - k]) % p;#include <bits/stdc++.h>
using namespace std;
const int N = 200, p = 1e6 + 7;
int dp[N][N], n, m, a[N];int main()
{cin >> n >> m;// 输入花的种类数n和目标数mfor (int i = 1; i <= n; i++) cin >> a[i];// 输入每种花的数量for (int i = 0; i <= a[1]; i++) dp[1][i] = 1;// 初始化第一种花的情况,因为只有一种花,所以可以从0到a[1]朵任意选择,都只有一种方式// 动态规划填表过程for (int i = 2; i <= n; i++) { // 遍历每一种花 for (int j = 0; j <= m; j++) { // 遍历当前要选的花的总数for (int k = 0; k <= a[i] && j - k >= 0; k++) {// 状态转移方程:dp[i][j]表示前i种花选出j朵的方式数,它等于前i - 1种花选出j - k朵的方式数之和dp[i][j] = (dp[i][j] + dp[i - 1][j - k]) % p;}}}cout << dp[n][m];// 输出结果,即前n种花选出m朵的方式数(模p意义下)return 0;
}思路二:
确定状态:
首先,需要明确问题的要求:给定n种不同的花和每种花的最大数量限制,求出在摆放m盆花时,能够形成的不同摆花方案数。这个问题的关键在于每种花可以选择摆放的数量从0到其最大限制,且摆放的花必须按照花的种类顺序排列。

在动态规划中,定义状态是至关重要的一步。这里,我们定义状态dp[i][j]为考虑前i种花时,摆放j盆花的不同方案数。
int n, m; cin >> n >> m;
vector<int>a(n + 1);
vector<vector<int> >dp(101, vector<int>(101));初始化:
对于本问题,我们知道不摆放任何花(即j=0时)只有一种方案,即什么花都不摆。因此,初始化dp[0][0] = 1,表示没有花时,摆放0盆花的方案数为1。其他情况(即当j>0时),在没有考虑任何花的情况下是不可能摆放任何花的,这些状态默认为0,反映了不可能发生的情况。
dp[0][0] = 1;循环遍历:
-
外层循环遍历花的种类:从1到
n,(花的种类为0时情况已初始化)对每种花进行遍历。 -
中层循环遍历目标花的总数:从0到
m,对可能摆放的花的总数进行遍历。 -
内层循环遍历当前种类花的可能数量:从0到当前种类花的数量限制或
j中的较小值(因为不可能摆放超过总数j的花)。这一步是优化的关键,通过只遍历到min(a[i], j)来减少不必要的计算。
for (int i = 1; i <= n; i++){for (int j = 0; j <= m; j++){for (int k = 0; k <= min(a[i],j); k++){......}}}状态转移方程:

dp[i][j] = (dp[i][j] + dp[i - 1][j - k]) % p;#include <bits/stdc++.h>
using namespace std;
const int p = 1e6 + 7;int main()
{int n, m; cin >> n >> m;vector<int>a(n + 1);vector<vector<int> >dp(101, vector<int>(101));for (int i = 1; i <= n; i++){cin >> a[i];}dp[0][0] = 1;for (int i = 1; i <= n; i++){for (int j = 0; j <= m; j++){for (int k = 0; k <= min(a[i],j); k++){dp[i][j] = (dp[i][j] + dp[i - 1][j - k]) % p;}}}cout << dp[n][m] % p;
}二、数字三角形加强版
数字三角形最大路径和问题
给定一个数字三角形,从三角形的顶部到底部有多条不同的路径。对于每条路径,把路径上的数加起来可以得到一个和。任务是找到最大的和。
路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右边的那个数。此外,向左下走的次数与向右下走的次数相差不能超过1。
输入描述:
输入的第一行包含一个整数N(1≤N≤100),表示三角形的行数。下面的N行给出数字三角形。数字三角形上的数都是0至100之间的整数。
输出描述:
输出一个整数,表示最大路径和。
输入输出样例:
输入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
输出:
27
数字三角形
http://t.csdnimg.cn/2IdF4
此题与之前这题的不同点在与多了一个这样的要求:
- 此外,向左下走的次数与向右下走的次数相差不能超过1。
意为:路径最后会停在最后一行中间的位置。此时有奇数和偶数两种情况,但是可以统一考虑为一种情况:
max(dp[n][(n + 1) / 2], dp[n][(n + 2) / 2]);如果是奇数,那么两个数值相同;如果是偶数,取更大的一个,皆符合题意。
#include <iostream>
using namespace std;
int a[200][200], dp[200][200], n;
int main()
{cin >> n;for (int i = 1; i <= n; i++)for (int j = 1; j <= i; j++)cin >> a[i][j];dp[1][1] = a[1][1];for (int i = 2; i <= n; i++)for (int j = 1; j <= i; j++)dp[i][j] = a[i][j] + max(dp[i - 1][j], dp[i - 1][j - 1]);cout << max(dp[n][(n + 1) / 2], dp[n][(n + 2) / 2]);return 0;
}
今天就先到这了!!!

看到这里了还不给博主扣个:
⛳️ 点赞☀️收藏 ⭐️ 关注!
你们的点赞就是博主更新最大的动力!
有问题可以评论或者私信呢秒回哦。
相关文章:

蓝桥杯练习题总结(三)线性dp题(摆花、数字三角形加强版)
目录 一、摆花 思路一: 确定状态: 初始化: 思路二: 确定状态: 初始化: 循环遍历: 状态转移方程: 二、数字三角形加强版 一、摆花 题目描述 小明的花店新开张,为了吸…...
 multi_match的使用)
Elasticsearch(15) multi_match的使用
elasticsearch version: 7.10.1 multi_match是Elasticsearch中的一种查询类型,允许在一个或多个字段上执行全文本搜索,并合并各个字段的结果得分。这种查询有助于实现跨多个字段的统一搜索体验。 语法 {"query": {"multi_m…...

nodejs的线程模型和libuv库的基本使用
文章目录 nodejs中集成addon本地代码的回调问题单线程事件驱动模型libuvlibuv基本框架addon中使用libuv代码nodejs中集成addon本地代码的回调问题 在C++的代码中,回调函数是一个基本的代码调用方式。而在我自己的开发实践中,需要在addon这样一个nodejs的本地化模块中实现一个…...
Uni-app/Vue/Js本地模糊查询,匹配所有字段includes和some方法结合使用e
天梦星服务平台 (tmxkj.top)https://tmxkj.top/#/ 1.第一步 需要一个数组数据 {"week": "全部","hOutName": null,"weekendPrice": null,"channel": "门市价","hOutId": 98,"cTime": "…...
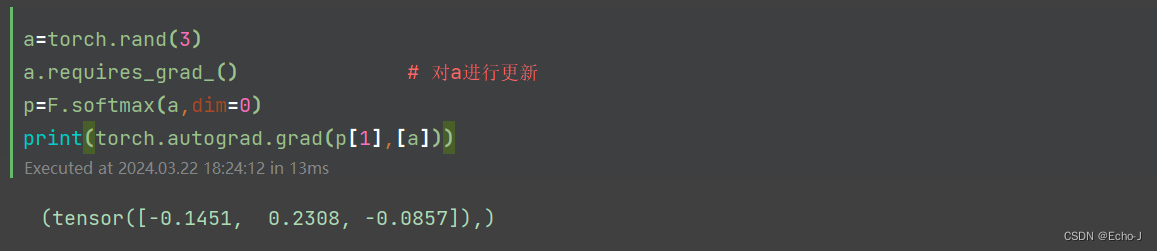
深度学习pytorch——激活函数损失函数(持续更新)
论生物神经元与神经网络中的神经元联系——为什么使用激活函数? 我们将生物体中的神经元与神经网络中的神经元共同分析。从下图可以看出神经网络中的神经元与生物体中的神经元有很多相似之处,由于只有刺激达到一定的程度人体才可以感受到刺激,…...

《苹果 iOS 应用开发与分发的关键问题解析》
一、背景 解决同事问的问题,来来回回被问好几次相同的问题,然后确认,我觉得不如写个文档 二、非研发人员安装iOS应用方式 TestFlightIPA 文件 对比 TestFlightIPA 文件安装方式TestFlight 是苹果提供的一个 beta 测试平台,开发者…...

爱上数据结构:顺序表和链表
一、线性表 线性表(linear list)是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使 用的数据结构,常见的线性表:顺序表、链表、栈、队列、字符串... 线性表在逻辑上是线性结构,也就说是连续的一条…...

python知识点总结(十)
python知识点总结十 1、装饰器的理解、并实现一个计时器记录执行性能,并且将执行结果写入日志文件中2、队列和栈的区别,并且用python实现3、设计实现遍历目录与子目录4、CPU处理进程最慢的情况通常发生在以下几种情况下:5、CPU处理线程最慢的…...

【Python】探索 Python 编程世界:常量、变量及数据类型解析
欢迎来CILMY23的博客 本篇主题为 探索 Python 编程世界:常量、变量及数据类型解析 个人主页:CILMY23-CSDN博客 Python系列专栏:http://t.csdnimg.cn/HqYo8 上一篇博客: http://t.csdnimg.cn/SEdbp C语言专栏: htt…...

vue页面实现左右div宽度,上下div高度分割线手动拖动高度或者宽度自动变化,两个div宽度或者高度拉伸调节,实现左右可拖动改变宽度的div内容显示区
实现左右或者上下div两部分拖动,宽度或者高度自动变化,实现流畅平滑的变化,还可以是实现拖动到一定宽度就不让拖动了,如果你不需要最小宽度,就直接去掉样式就行 这是页面。分左中右三部分,中间我是用来作为拖动的按钮…...

知攻善防应急靶场-Linux(1)
前言: 堕落了三个月,现在因为被找实习而困扰,着实自己能力不足,从今天开始 每天沉淀一点点 ,准备秋招 加油 注意: 本文章参考qax的网络安全应急响应和知攻善防实验室靶场,记录自己的学习过程&am…...

ffmpeg命令行
ffmpeg 如果要在linux gdb 调试,需要在configure 时候不优化 开启调试 ./configure --enable-debug --disable-optimizations make如何开启gdb 调试 gdb ffmpeg_gset args -i test.hevc -c:v copy -c:a copy output_265.mp4rh264 的流生成mp4 文件,不转…...
VMware虚拟机更换引导顺序
前言 我用wmware装了黑群晖测试,将img转成vmdisk的格式之后发现系统引导盘之后1G,有点太小了 我准备把wmware的黑群晖系统迁移到新添加的虚拟磁盘里 1.登录黑群晖的SSH 请先在黑群晖的控制面板中的终端机和SNMP里面启用SSH功能,才能使用ss…...
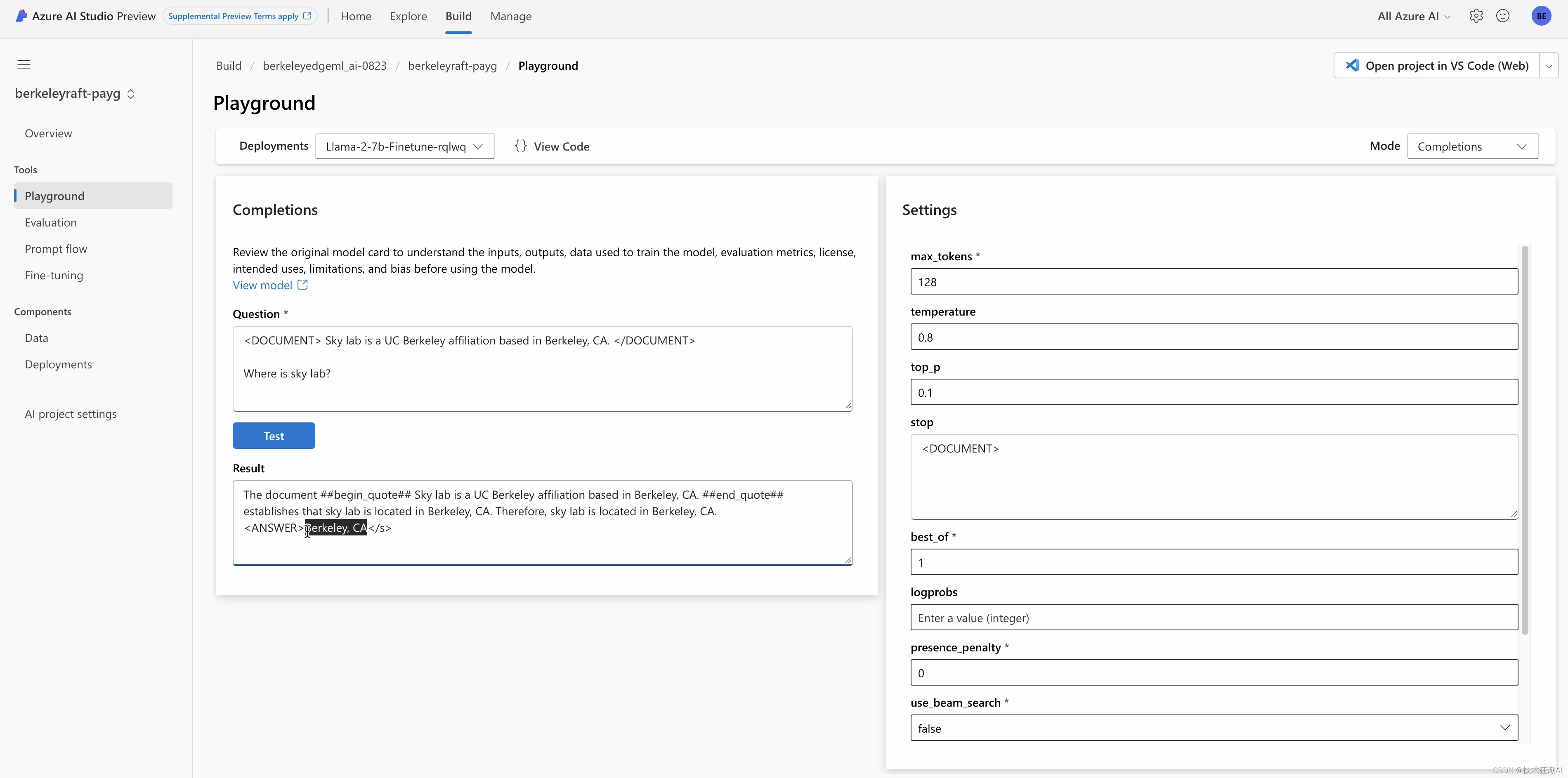
RAFT:让大型语言模型更擅长特定领域的 RAG 任务
RAFT(检索增强的微调)代表了一种全新的训练大语言模型(LLMs)以提升其在检索增强生成(RAG)任务上表现的方法。“检索增强的微调”技术融合了检索增强生成和微调的优点,目标是更好地适应各个特定领…...

Stable Diffusion 本地训练端口与云端训练端口冲突解决办法
方法之一,修改本地训练所用的端口 1 首先,进入脚本训练器的根目录 例如:C:\MarkDeng\lora-scripts-v1.7.3 找到gui.py 2 修改端口号 因为云端训练器也是占用28000和6006端口 那么本地改成27999和6007也是可以的 保存退出,运行启动…...

C++学习day1
思维导图 定义自己的命名空间,其中有string类型的变量,再定义两个函数,一个函数完成字符串的输入,一个函数完成求字符串长度,再定义一个全局函数完成对该字符串的反转 #include <iostream> using namespace std;…...

openGauss CM
CM 可获得性 本特性自openGauss 3.0.0版本开始引入。 特性简介 CM(Cluster Manager)是一款数据库管理软件,由cm_server和cm_agent组成。 cm_agent是部署在数据库每个主机上,用来启停和监控各个数据库实例进程的数据库管理组件…...
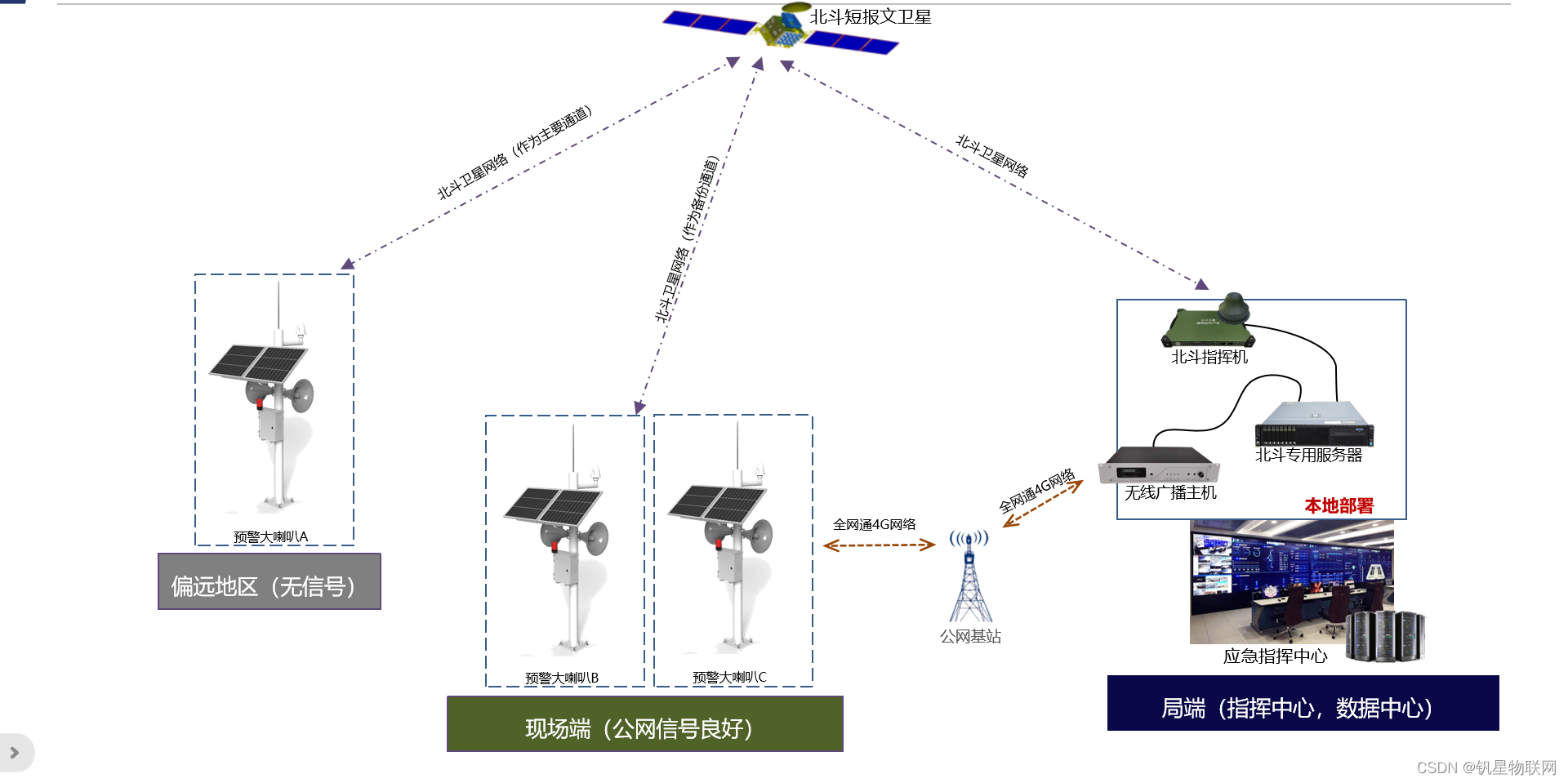
北斗短报文+4G应急广播系统:实时监控 自动预警 保护校园安全的新力量
安全无小事,生命重如山。学生是祖国的未来,校园安全是全社会安全工作的一个重要的组成部分。它直接关系到青少年学生能否安健康地成长,关系到千千万万个家庭的幸福安宁和社会稳定。 灾害事故和突发事件频频发生,给学生、教职员工…...

2024河北石家庄矿业矿山展览会|河北智慧矿山展会|河北矿博会
2024中国(石家庄)国际矿业博览会 时间:2024年7月4-6日 地点:石家庄国际会展中心.正定 随着全球经济的持续增长和矿产资源需求的不断攀升,矿业行业正迎来前所未有的发展机遇。作为矿业领域的盛会&…...

ruoyi使用笔记
1.限流处理 RateLimiter PostMapping("/createOrder") ApiOperation("创建充值订单") RateLimiter(key CacheConstants.REPEAT_SUBMIT_KEY,time 10,count 1,limitType LimitType.IP) public R createOrder(RequestBody Form form) {//业务处理return …...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
