拉普拉斯变换
定义:
拉普拉斯变换是一种在信号处理、控制理论和其他领域中广泛使用的数学工具,用于将一个函数从时域转换到复频域。拉普拉斯变换将一个函数 f(t) 变换为一个复变量函数 F(s),其中 s 是复数变量。下面是拉普拉斯变换的推导过程:
- 定义拉普拉斯变换:
给定一个函数 f(t),其拉普拉斯变换 F(s) 定义为:
F(s)=∫0∞e−stf(t)dt
其中,s 是一个复数变量。
- 计算拉普拉斯变换:
根据定义,我们可以计算函数 f(t) 的拉普拉斯变换 F(s)。首先,将 f(t) 乘以指数函数 e^{-st},然后对 t 从 0 到 无穷积分。这个积分可以是定积分,也可以是广义积分。
- 拉普拉斯变换的性质:
拉普拉斯变换具有一些重要的性质,例如线性性、时移性、频移性、频率缩放性等。这些性质可以简化计算,并在信号处理和控制系统分析中起到重要作用。
- 逆拉普拉斯变换:
给定一个复变量函数 F(s),其逆拉普拉斯变换 f(t) 定义为:
f(t)=12πj∫σ−j∞σ+j∞estF(s)ds
其中,逆拉普拉斯变换通过沿着一条垂直线积分来计算,该线位于复平面的某个实部值 σ 上。
通过拉普拉斯变换,我们可以将微分方程转换为代数方程,简化系统分析和控制设计。在 MATLAB 中,可以使用 laplace() 函数来计算函数的拉普拉斯变换,以及使用 ilaplace() 函数来计算逆拉普拉斯变换。
示例:
让我们通过一个具体的示例来演示如何使用拉普拉斯变换。考虑一个简单的微分方程:
dx(t)dt+2x(t)=5
我们将对该微分方程进行拉普拉斯变换,以便求解其解析解。
- 对微分方程进行拉普拉斯变换:
将微分方程中的变量 x(t) 及其导数进行拉普拉斯变换,得到:
sX(s)−x(0)+2X(s)=5s
其中,X(s) 是 x(t) 的拉普拉斯变换,x(0) 是初始条件。
- 求解 X(s):
整理上式,得到:
X(s)=5+x(0)+sx(0)s(s+2)
- 求逆拉普拉斯变换:
现在我们有 X(s) 的表达式,我们可以通过计算逆拉普拉斯变换来找到 x(t)。对于上面的 X(s) 表达式,我们可以使用部分分式分解来求逆拉普拉斯变换。
X(s)=As+Bs+2
解出 A 和 B 的值,然后计算逆拉普拉斯变换,得到 x(t) 的解析表达式。
- MATLAB 实现:
在 MATLAB 中,可以使用 laplace() 函数来计算微分方程的拉普拉斯变换,然后使用 ilaplace() 函数来计算逆拉普拉斯变换。下面是一个简单的 MATLAB 代码示例:
syms s t Xs
eqn = s*Xs - x0 + 2*Xs == 5/s;
Xs = solve(eqn, Xs);
xt = ilaplace(Xs);
通过这个示例,您可以了解如何使用拉普拉斯变换来解决微分方程,并通过 MATLAB 进行计算。
请求解y=qxn+(1-q)yn-1的传递函数
对于差分方程 ( y = qxn + (1-q)yn-1 ),我们可以将其转化为Z域的传递函数形式。
假设输入信号为 ( x[n] ),输出信号为 ( y[n] ),则差分方程可以表示为:
[ y[n] = qx[n] + (1-q)y[n-1] ]
对上述方程进行Z变换,得到传递函数形式为:
[ Y(z) = qX(z) + (1-q)z^{-1}Y(z) ]
进一步整理得到传递函数 ( H(z) ) 的表达式为:
[ H(z) = \frac{Y(z)}{X(z)} = \frac{q}{1 - (1-q)z^{-1}} ]
所以,传递函数为 ( H(z) = \frac{q}{1 - (1-q)z^{-1}} )。
使用matlab求解请求解y=qxn+(1-q)yn-1的传递函数
在 MATLAB 中,我们可以使用 ztrans 函数来求解给定差分方程的传递函数。首先,我们需要将差分方程表示成Z变换的形式,然后应用 ztrans 函数计算传递函数。
假设给定的差分方程是 ( y[n] = q x[n] + (1-q) y[n-1] ),我们将其转化为Z变换的形式:
[ Y(z) = qX(z) + (1-q)z^{-1}Y(z) ]
现在,我们可以使用MATLAB来计算传递函数。以下是在MATLAB中求解传递函数的示例代码:
syms z q; % 定义符号变量
X = 1; % 假设输入信号 X(z) 的Z变换为1(这里假设输入信号是单位脉冲)
Y = q*X + (1-q)*z^(-1)*Y; % 根据差分方程和Z变换的关系得到 Y(z)
H = Y/X; % 计算传递函数 H(z) = Y(z)/X(z)
H = simplify(H); % 对传递函数进行化简
disp(H); % 显示传递函数
在上述示例代码中,我们定义了符号变量 ( z ) 和 ( q ),然后假设输入信号 ( x[n] ) 的Z变换为1(这里假设输入信号是单位脉冲)。接下来根据差分方程和Z变换的关系求解 ( Y(z) ),然后计算传递函数 ( H(z) = \frac{Y(z)}{X(z)} ),最后对传递函数进行化简并显示结果。
通过上述步骤,我们就可以使用MATLAB求解给定差分方程的传递函数了。
相关文章:

拉普拉斯变换
定义: 拉普拉斯变换是一种在信号处理、控制理论和其他领域中广泛使用的数学工具,用于将一个函数从时域转换到复频域。拉普拉斯变换将一个函数 f(t) 变换为一个复变量函数 F(s),其中 s 是复数变量。下面是拉普拉斯变换的推导过程:…...

Mashup-Math_Topic_One
Tutorial and Introspection A Rudolf and 121 注意到第 1 1 1 位只能被第 2 2 2 位影响,以此类推位置,对于 a i a_i ai , 如果 < 0 < 0 <0 ,不合法 ; 否则, a i − a i , a i 1 − 2 ∗ a i , a i 2 − a …...
基于JavaWEB SSM SpringBoot婚纱影楼摄影预约网站设计和实现
基于JavaWEB SSM SpringBoot婚纱影楼摄影预约网站设计和实现 博主介绍:多年java开发经验,专注Java开发、定制、远程、文档编写指导等,csdn特邀作者、专注于Java技术领域 作者主页 央顺技术团队 Java毕设项目精品实战案例《1000套》 欢迎点赞 收藏 ⭐留言…...
逐步学习Go-Select多路复用
概述 这里又有多路复用,但是Go中的这个多路复用不同于网络中的多路复用。在Go里,select用于同时等待多个通信操作(即多个channel的发送或接收操作)。Go中的channel可以参考我的文章:逐步学习Go-并发通道chan(channel)…...

王道:OJ15
课时15作业 Description 读取10个元素 87 7 60 80 59 34 86 99 21 3,然后建立二叉查找树,排序后输出3 7 21 34 59 60 80 86 87 99,针对有序后的元素,存入一个长度为10的数组中,通过折半查找找到21的下标(…...
【案例·查】数据类型强制转换,方便查询匹配
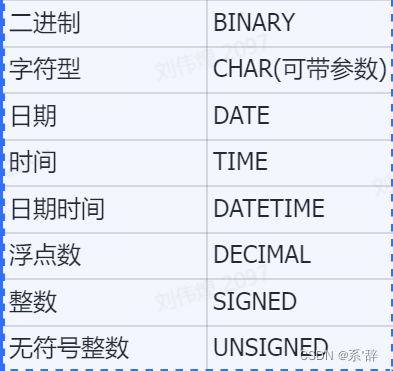
问题描述: MySQL执行中需要将某种数据类型的表达式显式转换为另一种数据类型,可以使用 SQL 中的cast()来处理 案例: SELECT CAST(9.0 AS decimal) #String化为小数类型SELECT * FROM table_1 WHERE 1888-03-07 CAST(theDate AS DATE) …...
spring boot3自定义注解+拦截器+Redis实现高并发接口限流
⛰️个人主页: 蒾酒 🔥系列专栏:《spring boot实战》 🌊山高路远,行路漫漫,终有归途 目录 写在前面 内容简介 实现思路 实现步骤 1.自定义限流注解 2.编写限流拦截器 3.注册拦截器 4.接口限流测试 写在前…...
使用certbot为网站启用https
1. 安装certbot客户端 cd /usr/local/bin wget https://dl.eff.org/certbot-auto chmod ax ./certbot-auto 2. 创建目录和配置nginx用于验证域名 mkdir -p /data/www/letsencryptserver {listen 80;server_name ~^(?<subdomain>.).ninvfeng.com;location /.well-known…...

Unity 背包系统中拖拽物体到指定位置或互换位置效果的实现
在Unity中,背包系统是一种常见的游戏系统,可以用于管理和展示玩家所持有的物品、道具或装备。 其中的拖拽功能非常有意思,具体功能就是玩家可以通过拖拽物品图标来移动物品在背包中的位置,或者将物品拖拽到其他位置或界面中&…...
iOS客户端自动化UI自动化airtest+appium从0到1搭建macos+脚本设计demo演示+全网最全最详细保姆级有步骤有图
Android客户端自动化UI自动化airtest从0到1搭建macos脚本设计demo演示全网最全最详细保姆级有步骤有图-CSDN博客 避坑系列-必读: 不要安装iOS-Tagent ,安装appium -这2个性质其实是差不多的都是为了安装wda。注意安装appium最新版本,安装完…...

每周编辑精选|在线运行 Deepmoney 金融大模型、AI 偏好等多个优质数据集上线
目前,AI 领域对金融模型的研究成果大多是基于公共知识进行训练的,但在实际的金融实践中,这些公共知识对于当前市场的可解释性往往严重不足。一个理想的金融大模型应该能够理解新闻或数据事件,并能够即时地从主观和量化两个角度对事…...
C++多重继承与虚继承
多重继承的原理 多重继承(multiple inheritance)是指从多个直接基类中产生派生类的能力。 多重继承的派生类继承了所有父类的属性。 在面向对象的编程中,多重继承意味着一个类可以从多个父类继承属性和方法。 就像你有一杯混合果汁,它是由多种水果榨取…...

请简单介绍一下Shiro框架是什么?Shiro在Java安全领域的主要作用是什么?Shiro主要提供了哪些安全功能?
请简单介绍一下Shiro框架是什么? Shiro框架是一个强大且灵活的开源安全框架,为Java应用程序提供了全面的安全解决方案。它主要用于身份验证、授权、加密和会话管理等功能,可以轻松地集成到任何Java Web应用程序中,并提供了易于理解…...

TouchGFX之Button
TouchGFX中的按钮是一种感应触控事件的控件,能够在按钮被按下/释放时发送回调 代码 #ifndef TOUCHGFX_ABSTRACTBUTTON_HPP #define TOUCHGFX_ABSTRACTBUTTON_HPP #include <touchgfx/Callback.hpp> #include <touchgfx/events/ClickEvent.hpp> #includ…...
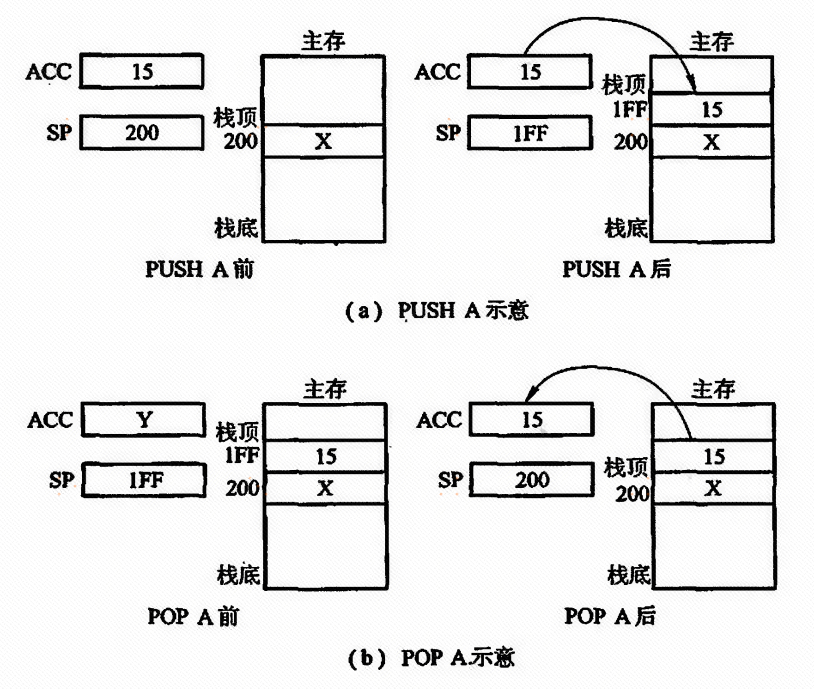
计算机组成原理 — 指令系统
指令系统 指令系统指令的概述指令的格式指令的字长取决于 操作数类型和操作种类操作数的类型数据在存储器中的存放方式操作类型 寻址方式指令寻址数据寻址立即寻址直接寻址隐含寻址间接寻址寄存器寻址寄存器间接寻址基址寻址变址寻址堆栈寻址 RISC 和 CISC 技术RISC 即精简指令…...

使用easyYapi生成文档
easyYapi生成文档 背景1.安装配置1.1 介绍1.2 安装1.3 配置1.3.1 Export Postman1.3.2 Export Yapi1.3.3 Export Markdown1.3.4 Export Api1.3.6 常见问题补充 2. java注释规范2.1 接口注释规范2.2 出入参注释规范 3. 特定化支持3.1 必填校验3.2 忽略导出3.3 返回不一致3.4 设置…...

蓝桥杯练习题总结(三)线性dp题(摆花、数字三角形加强版)
目录 一、摆花 思路一: 确定状态: 初始化: 思路二: 确定状态: 初始化: 循环遍历: 状态转移方程: 二、数字三角形加强版 一、摆花 题目描述 小明的花店新开张,为了吸…...
 multi_match的使用)
Elasticsearch(15) multi_match的使用
elasticsearch version: 7.10.1 multi_match是Elasticsearch中的一种查询类型,允许在一个或多个字段上执行全文本搜索,并合并各个字段的结果得分。这种查询有助于实现跨多个字段的统一搜索体验。 语法 {"query": {"multi_m…...

nodejs的线程模型和libuv库的基本使用
文章目录 nodejs中集成addon本地代码的回调问题单线程事件驱动模型libuvlibuv基本框架addon中使用libuv代码nodejs中集成addon本地代码的回调问题 在C++的代码中,回调函数是一个基本的代码调用方式。而在我自己的开发实践中,需要在addon这样一个nodejs的本地化模块中实现一个…...
Uni-app/Vue/Js本地模糊查询,匹配所有字段includes和some方法结合使用e
天梦星服务平台 (tmxkj.top)https://tmxkj.top/#/ 1.第一步 需要一个数组数据 {"week": "全部","hOutName": null,"weekendPrice": null,"channel": "门市价","hOutId": 98,"cTime": "…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
