包子凑数(蓝桥杯,闫氏DP分析法)
题目描述:
小明几乎每天早晨都会在一家包子铺吃早餐。
他发现这家包子铺有 N 种蒸笼,其中第 i 种蒸笼恰好能放 Ai 个包子。
每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买 X 个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有 X 个包子。
比如一共有 3 种蒸笼,分别能放 3、4和 5 个包子。
当顾客想买 11个包子时,大叔就会选 2 笼 3 个的再加 1 笼 5 个的(也可能选出 1 笼 3 个的再加 2 笼 4 个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。
比如一共有 3 种蒸笼,分别能放 4、5和 6 个包子。
而顾客想买 7 个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。
输入格式:
第一行包含一个整数 N。
接下来 N 行,每行包含一个整数 Ai。
输出格式:
输出一个整数代表答案。
如果凑不出的数目有无限多个,输出INF。
数据范围:
1≤N≤100,
1≤Ai≤100
输入样例1:
2
4
5
输出样例1:
6
输入样例2:
2
4
6
输出样例2:
INF
样例解释
对于样例1,凑不出的数目包括:1, 2, 3, 6, 7, 11。
对于样例2,所有奇数都凑不出来,所以有无限多个。
前情提要:这道题目有关完全背包,01背包这两道题目,如果没看过这两道题目的题解大家可以去看看,能帮助理解这道题目。链接我也放到这里了,点击链接就行。
分析步骤:
第一:看到题目我们就能明白,每一笼包子是可以选无数多笼的,只要次数不超过我们指定的个数,看看能组合出多少种组合来,最后判断一下有多少个数组合出来了,多少个数没有组合出来那么这就是答案。由此可以得出第一个特点:题目是 组合问题,是完全背包问题的变形:有几个物品,每个物品无限个,每个物品选任意个,能否凑到某个重量。
第二:我们如何判断这个题目是否有无数个值会组合不出来呢?我们想一下什么样的就组合不出来,例如2,4,6最大公约数是2所以奇数组合不出来,因为他只能组合出gcd的倍数。例如30,60最大公约数是30,所以只要不是30的倍数的就一定组合不出来,由此我们可以发现一些问题组合数和gcd有关,只要gcd不是1的话那么它就有无数种数组合不出来。这里用到裴蜀定理 ,任意两个数的组合必定是他们gcd的倍数,同样可以推广到更多数:如果这些数的gcd的d不是1那么有无数个数组合不出来
第三:闫氏DP分析法:
-
根据闫氏DP分析法我们可以知道dp问题可以将其分解为两个步骤:第一种是状态表示,第二种是状态计算。
-
我们所有的背包问题都是围绕我们对于集合的定义来的,所以这个定义是非常重要的!!!我们将集合定义为:所有只从前i个包子中选择,数量为j的集合是否能够达到题目要求的包子数,是个bool数组。
-
状态计算:由于完全背包是可以无限次的选择物品的,所以我们不能和01背包一样,只将其分解为选或者不选,因为它可以有很多很多种选择,可以不选,可以选一种,可以选两种...只要题目要求包子数量(背包体积)足够大就可以。
-
如果他不选择包子 i 那么这种情况相当于从(1,i - 1)中选择数量不超过j的情况是一样的所以我们的表达式是:f[i-1][j]。
-
如果他选择物品 i 那么这样又该如何表示呢?我们并不知道他到底要选择几个物品,那应该怎么做呢?假如我们选择一个的话那么就应该写为f[i-1][j-vi];假如我们选择两个的话那么就应该写为f[i-1][j-2*vi];假如我们选择k个的话那么就应该写为f[i-1][j-k*vi],那么我们最终的答案就应该在这些集合之中。
-
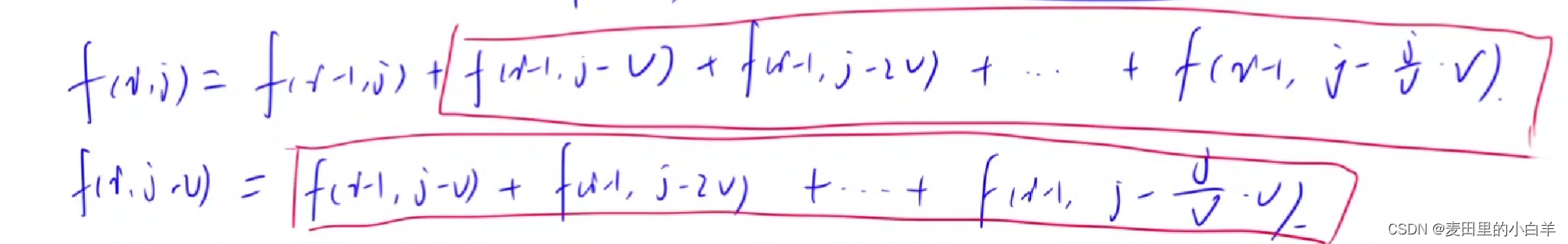
-
所以f(i,j) = f(i-1 , j) || f(i-1 , j - v) || f(i-1 , j - 2v) || ........|| f(i-1 , j - (j/v)*v);
-
所以f(i,j-v) = f(i-1 , j - v) || f(i-1 , j - 2*v) || f(i-1 , 3*v) || ........f(i-1 , j - (j/v)*v);
-
由上述两个式子,我们可以知道如果将 j 替换成 j-vi 两个式子非常相似。f[ i ] [ j ] = f[ i -1][ j ] || f[ i ][ j - vi ] ;
第四:书写主函数,构建整体框架:
-
输入值,并且根据裴蜀定理求出最大公约数看看是不是1,如果不是1那么必定有无数个值组合不出来,那么直接输出INF。初始化一下我们的f数组全部赋值为0,初始化我们的f[0][0] = true。为什么?根据我们对集合的定义来分析:只从前i个包子中选择,数量为j的集合是否能够达到题目要求的包子数。那么f[0][0]代表前0个包子中选择,数量为0的集合是可能的所以初始化为true。
for(int i = 1 ; i <= n ; ++ i){for(int j = 0 ; j <= 10000 ; ++ j){f[i][j] = f[i-1][j] || (j >= arr[i] ? f[i][j - arr[i]] : false) ;}} -
d==1 的话我们就进入双重for循环。第一个for就是包子种类,第二个for就是包子数量。那么问题来了。我们怎么确定数量最大值就是10000呢?那么当qcd为1时,最大不能表示出来的数必定有个上界,因为两个数a,b(当gcd=1时),最大不能表示出数是:(a-1)(b-1)-1。当数字更多的时候,这个上界必然更小(可选的数字变多了),而99和98是100内最大的互质的数,所以这个上界选择10000。
-
我们之前分析出了f[ i ] [ j ] = f[ i -1][ j ] || f[ i ][ j - vi ] ;但是注意一个问题:选择一个,选择两个,是在所需包子数大于我们的这一笼包子数的情况下才可以选,假如所需包子数都要小于这一笼包子数的话就不可以选了!所以我们选择了用三目运算符 (j >= arr[i] ? f[i][j - arr[i]] : false) ;这句话的意思是如果 j >= arr[i] 是对的话那么则返回f[i][j - arr[i]] ;如果不对则返回false,那么f[ i ] [ j ] = f[ i -1][ j ] || f[ i ][ j - vi ]这就是错了就代表组合不出这个数。
-
最后我们只需要在遍历一遍,看看哪些数是组合不出来的,组合不出来就res++。
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 110 ;int n ;
bool f[N][10010];
int arr[N];int gcd(int a , int b){return b ? gcd(b,a%b):a;
}int main()
{cin>>n;int d = 0;for(int i = 1 ; i <= n ; ++i){cin>>arr[i];d = gcd(d,arr[i]);}memset(f, 0, sizeof f);f[0][0] = true;if(d != 1) cout<<"INF"<<endl;else{for(int i = 1 ; i <= n ; ++ i){for(int j = 0 ; j <= 10000 ; ++ j){f[i][j] = f[i-1][j] || (j >= arr[i] ? f[i][j - arr[i]] : false) ;}}int res = 0;for(int i = 0 ; i <= 10000 ; i ++){if(!f[n][i]) res ++;}cout<<res;
}return 0;
}
01背包从后往前,完全背包从前往后!!
相关文章:
包子凑数(蓝桥杯,闫氏DP分析法)
题目描述: 小明几乎每天早晨都会在一家包子铺吃早餐。 他发现这家包子铺有 N 种蒸笼,其中第 i 种蒸笼恰好能放 Ai 个包子。 每种蒸笼都有非常多笼,可以认为是无限笼。 每当有顾客想买 X 个包子,卖包子的大叔就会迅速选出若干笼…...

Java八股文(JVM)
Java八股文のJVM JVM JVM 什么是Java虚拟机(JVM)? Java虚拟机是一个运行Java字节码的虚拟机。 它负责将Java程序翻译成机器代码并执行。 JVM的主要组成部分是什么? JVM包括以下组件: ● 类加载器(ClassLoa…...

云硬盘扩容后将空间增加到原有分区的解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...
Tensorflow2.0笔记 - metrics做损失和准确度信息度量
本笔记主要记录metrics相关的内容,详细内容请参考代码注释,代码本身只使用了Accuracy和Mean。本节的代码基于上篇笔记FashionMnist的代码经过简单修改而来,上篇笔记链接如下: Tensorflow2.0笔记 - FashionMnist数据集训练-CSDN博…...

LeetCode 面试经典150题 290.单词规律
题目: 给定一种规律 pattern 和一个字符串 s ,判断 s 是否遵循相同的规律。 这里的 遵循 指完全匹配,例如, pattern 里的每个字母和字符串 s 中的每个非空单词之间存在着双向连接的对应规律。 思路:一一映射需要用到…...
)
【CASS精品教程】CASS中计算四参数和七参数(以RTK数据为例)
文章目录 一、四参数介绍二、四参数计算三、七参数介绍四、四参数、七参数的区别一、四参数介绍 两个不同的二维平面直角坐标系之间转换通常使用四参数模型,四参数适合小范围测区的空间坐标转换,相对于七参数转换的优势在于只需要2个公共已知点就能进行转换,操作简单。 在…...

什么是RISC-V?开源 ISA 如何重塑未来的处理器设计
RISC-V代表了处理器架构的范式转变,特点是其开源模型简化了设计理念并促进了全球community-driven的开发。RISC-V导致了处理器技术发展前进方式的重大转变,提供了一个不受传统复杂性阻碍的全新视角。 RISC-V起源于加州大学伯克利分校的学术起点ÿ…...

展馆设计中展示有哪些要求
1、展示产品特点和功能 产品展示应突出产品的特点、功能和优势。通过使用适当的展示方式和展示环境,使观众能够直观地了解产品的外观、结构、性能等方面。可以使用实物展示、模型、原型、图表、动画等方式,以多种角度和视角展示产品的特点和功能。 2、提…...
python实战之PyQt5桌面软件
一. 演示效果 二. 准备工作 1. 使用pip 下载所需包 pyqt5 2. 下载可视化UI工具 QT Designer 链接:https://pan.baidu.com/s/1ic4S3ocEF90Y4L1GqYHPPA?pwdywct 提取码:ywct 3. 可视化UI工具汉化 把上面的链接打开, 里面有安装和汉化包, 前面的路径还要看…...
Switch 和 PS1 模拟器:3000+ 游戏随心玩 | 开源日报 No.174
Ryujinx/Ryujinx Stars: 26.1k License: MIT Ryujinx 是用 C# 编写的实验性任天堂 Switch 模拟器。 该项目旨在提供出色的准确性和性能、用户友好的界面以及稳定的构建。它已经通过了大约 4050 个测试,其中超过 4000 个可以启动并进入游戏,其中大约 340…...
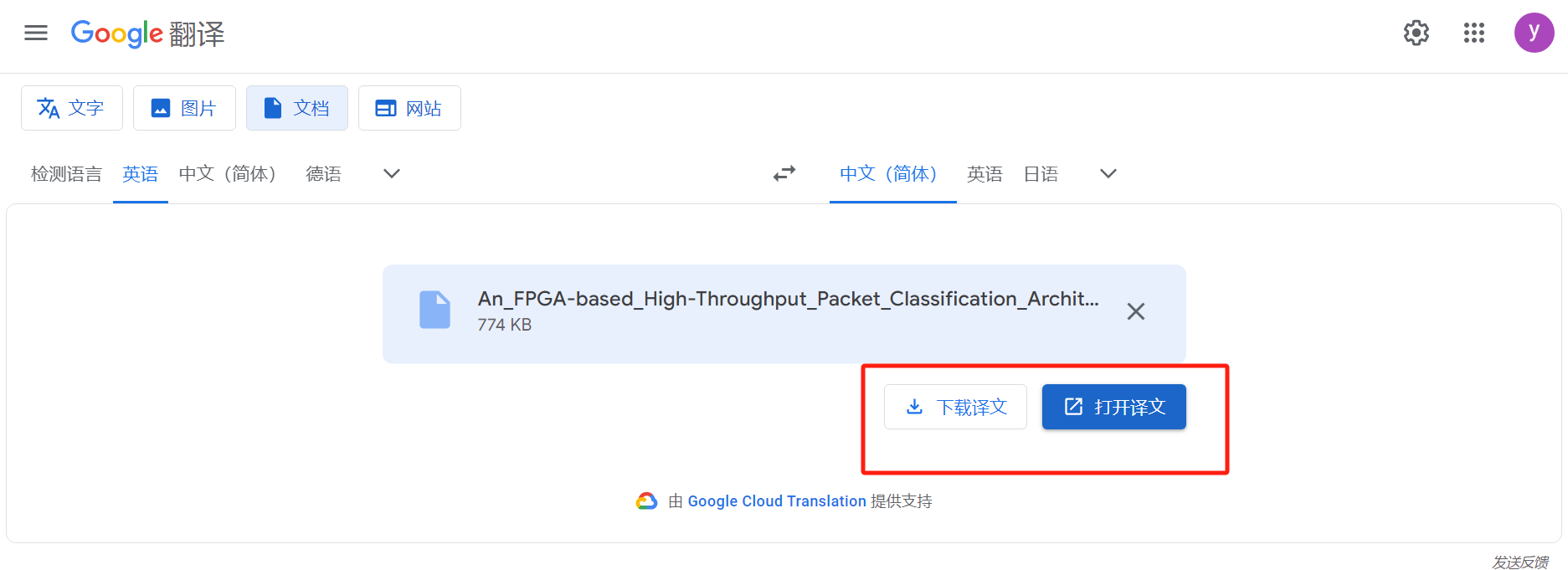
免费翻译pdf格式论文
进入谷歌翻译网址https://translate.google.com/?slauto&tlzh-CN&opdocs 将需要全文翻译的pdf放进去 选择英文到中文,然后点击翻译 可以选择打开译文或者下载译文,下载译文会下载到电脑上,打开译文会在浏览器打开。...

3D产品可视化SaaS
“我们正在走向衰退吗?” “我们已经陷入衰退了吗?” “我们正在步入衰退。” 过去几个月占据头条的问题和陈述引发了关于市场对每个行业影响的讨论和激烈辩论。 特别是对于科技行业来说,过去几周一直很动荡,围绕费用、增长和裁…...

浙大版《C语言程序设计(第4版)》题目集-习题3-5 三角形判断
给定平面上任意三个点的坐标(x1,y1)、(x2,y2)、(x3,y3),检验它们能否构成三角形。 输入格式: 输入在一行中顺序给出六个[−100,100]范围内的数字,即三个点的坐标x1、y1、x2、y2、x3、y3。 输出格式: 若这3个点不能构成三角形,则在一行中输…...

Java封装、继承、多态和抽象深度解析
在软件工程的世界里,面向对象编程(OOP)是一种编程范式,它使用“对象”来设计软件。对象可以封装数据和方法,以提高代码的复用性、可维护性和可扩展性。Java作为一门面向对象的编程语言,提供了四个基本的面向…...
深度学习每周学习总结P3(天气识别)
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 | 接辅导、项目定制 数据链接 提取码:o3ix 目录 0. 总结1. 数据导入部分数据导入部分代码详解:a. 数据读取部分a.1 提问:关…...

通过iOS网络抓包工具实现移动应用数据安全监控
摘要 本文将深入探讨iOS平台上常用的网络抓包工具,包括Charles、克魔助手、Thor和Http Catcher,以及通过SSH连接进行抓包的方法。此外,还介绍了克魔开发助手作为iOS应用开发的辅助工具,提供的全方面性能监控和调试功能。 在iOS应…...

Stable Diffusion WebUI 生成参数:脚本(Script)——提示词矩阵、从文本框或文件载入提示词、X/Y/Z图表
本文收录于《AI绘画从入门到精通》专栏,专栏总目录:点这里,订阅后可阅读专栏内所有文章。 大家好,我是水滴~~ 在本篇文章中,我们将深入探讨 Stable Diffusion WebUI 的另一个引人注目的生成参数——脚本(Script)。我们将逐一细说提示词矩阵、从文本框或文件导入提示词,…...

synchronized和volatile的原理及应用
文章目录 synchronized的实现原理及应用升级锁代码示例volatile原理及应用代码示例线程不安全类 synchronized的实现原理及应用 synchronized 是Java中用于实现线程同步的关键字,可以应用于方法或代码块,确保在多线程环境下对共享资源的安全访问。下面是…...

Python 基于 OpenCV 视觉图像处理实战 之 OpenCV 简单实战案例 之九 简单闪烁效果
Python 基于 OpenCV 视觉图像处理实战 之 OpenCV 简单实战案例 之九 简单闪烁效果 目录 Python 基于 OpenCV 视觉图像处理实战 之 OpenCV 简单实战案例 之九 简单闪烁效果 一、简单介绍 二、简单闪烁效果实现原理 三、简单闪烁效果案例实现简单步骤 四、注意事项 一、简单…...

11 开源鸿蒙OpenHarmony轻量系统源码分析
开源鸿蒙轻量系统源码分析 作者将狼才鲸日期2024-03-28 一、前言 之前单独的LiteOS是通过Makefile编译的,当前的开源鸿蒙LiteOS-M和LiteOS-A是通过gn和ninja编译的。 Gitee官方只介绍了LiteOS-M的gn ninja编译的流程,针对M3使用Keil编译的流程可能要参…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

