【数据结构 | 图论】如何用链式前向星存图(保姆级教程,详细图解+完整代码)
一、概述
链式前向星是一种用于存储图的数据结构,特别适合于存储稀疏图,它可以有效地存储图的边和节点信息,以及边的权重。
它的主要思想是将每个节点的所有出边存储在一起,通过数组的方式连接(类似静态数组实现链表)。这种方法的优点是存储空间小,查询速度快,尤其适合于处理大规模的图数据,在一些笔试或者竞赛的场景中经常使用。
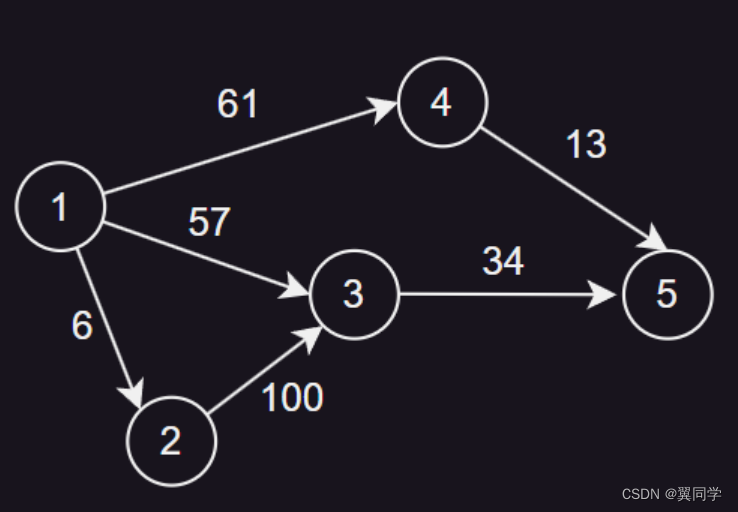
下面,我们用这张图来图解一下链式前向星的存储逻辑:
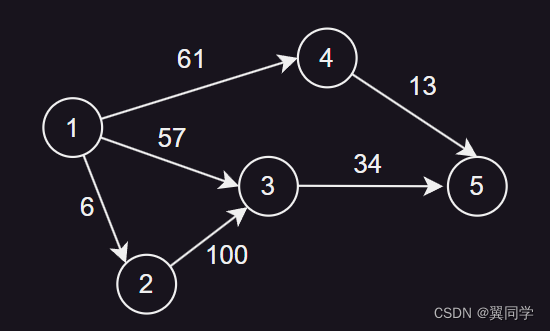
二、前置准备
注意看这里的设定,以及我加粗的提示。
-
head数组:head[i]存储的是节点i的第一条边的编号。这样,我们可以通过head[i]快速找到从节点i出发的所有边。 -
next数组:next[j]存储的是编号为j的边的下一条边的编号。这样,我们可以通过next[j]快速找到从同一个节点出发的下一条边。 -
to数组:to[j]存储的是编号为j的边的终点节点编号。这样,我们可以通过to[j]快速找到边j的终点,也就是这条边要去往哪里。 -
weight数组:weight[j]存储的是编号为j的边的权重。这样,我们可以通过weight[j]快速找到边j的权重。 -
cnt变量:cnt用于存储边的数量,也表示边的编号。每添加一条边,cnt就会增加1。这样,我们可以通过cnt快速知道当前图中边的数量,同时我们也认为cnt是新添加边的编号。
三、初始化
public static void build(int n) {cnt = 1; // 边从1开始编号Arrays.fill(head, 1, n + 1, 0); // head[1 ... n] 全设为 0
}
在链式前向星中,我们使用cnt来作为边的编号,由于边的编号是从1开始的,所以初始化时我们将cnt设置为1。同时,将head数组的所有元素设置为0。因为head[i]存储的是节点i的第一条边的编号,所以,如果节点i没有出度(即没有从节点i出发的边),那么head[i]就应该为0。初始化时所有节点都没有出度,后续在添加边的时候,会更新对应的head[i]的值。
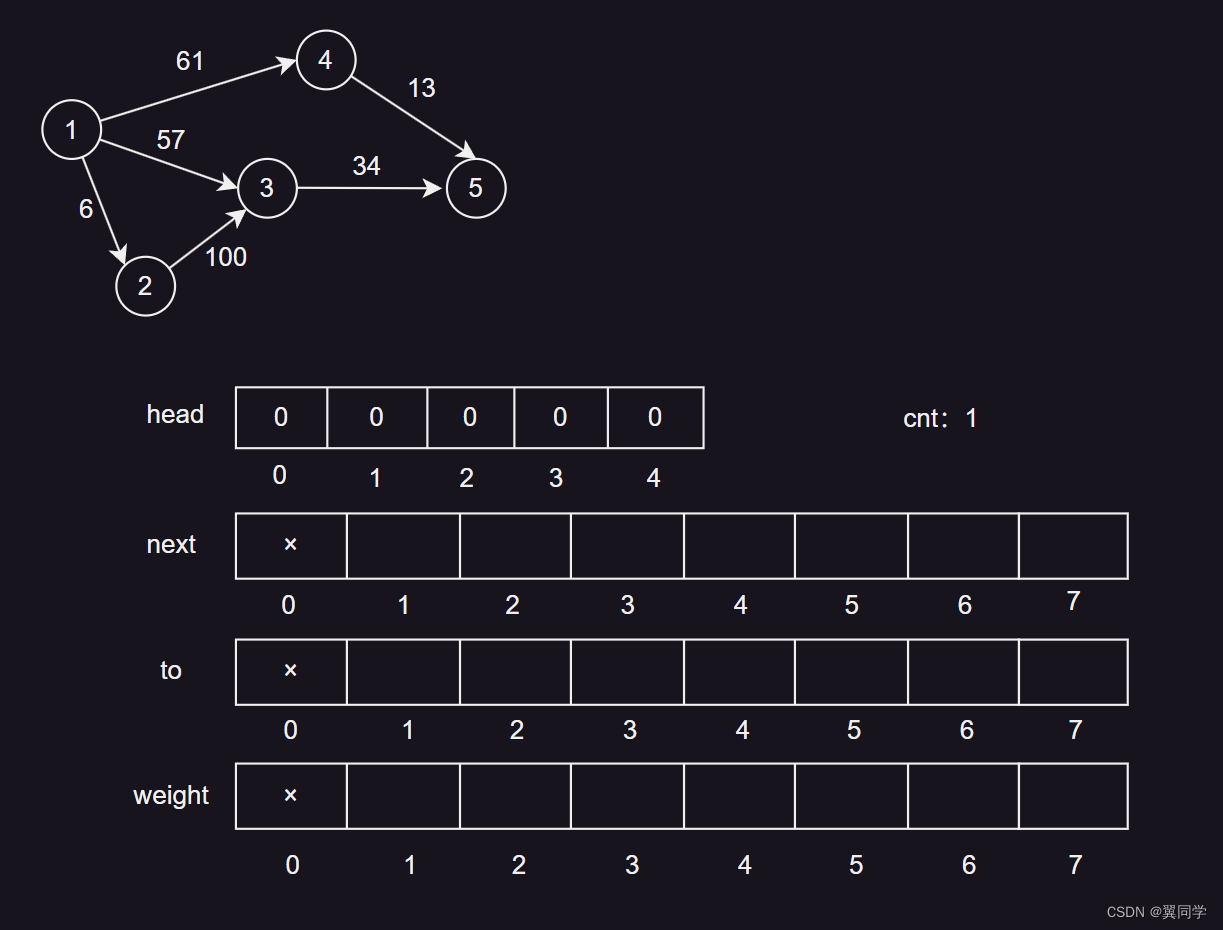
四、添加边(重点)
在链式前向星中添加边的操作是最核心的,它涉及到head、next、to、weight数组的更新,以及边的编号cnt的自增。
在看代码之前,我们先回顾一下各个结构的下标以及值的含义:
-
head数组:下标i表示节点编号,值head[i]表示从节点i出发的第一条边的编号。 -
next数组:下标j表示边的编号,值next[j]表示编号为j的边的下一条边的编号。 -
to数组:下标j表示边的编号,值to[j]表示编号为j的边的终点节点编号。 -
weight数组:下标j表示边的编号,值weight[j]表示编号为j的边的权重。
结合上述含义,我们来看代码就很清晰了:
// (u, v, w): 有一条边,从u节点指向v节点,权重为w
// 在每一次添加边时,cnt都表示当前未分配的边的编号,添加边后cnt需++
public static void addEdge(int u, int v, int w) {next[cnt] = head[u];to[cnt] = v;weight[cnt] = w;head[u] = cnt;++cnt;
}
首先,我们需要更新next数组。next[cnt]存储的是编号为cnt的边的下一条边的编号。在添加新边时,我们将新边的next置为旧的头边号head[u],这样就可以通过next[cnt]快速找到从节点u出发的下一条边。
然后,我们需要更新to数组,将新边的终点设置为v,这样就可以通过to[cnt]快速找到边cnt的终点。
更新weight数组也很自然,就是将新边的权重设置为w,最后,我们将节点u的头边号修改为当前新边的编号,这样就可以通过head[u]快速找到从节点u出发的第一条边。
备注:记得每添加一条边,边的编号
cnt就需要增加1
五、建图
建图分为有向图与无向图,输入的参数是一个二维数组edges作为输入,这个数组的每个元素都是一个长度为3的数组,代表一条边的两个端点和这条边的权重。
// 建有向图
public static void directGraph(int[][] edges) {for (int[] edge : edges) {addEdge(edge[0], edge[1], edge[2]); // 添加有向边}
}// 建无向图
public static void undirectGraph(int[][] edges) {for (int[] edge : edges) {addEdge(edge[0], edge[1], edge[2]); // 添加边addEdge(edge[1], edge[0], edge[2]); // 添加反向边}
}
六、图解
下面这个数组提供了图的边信息,基本上题目都会给定形式的信息,让你去建图:
有一条边(u, v, w),表示从u节点指向v节点,权重为w
[[1, 6, 2],[1, 3, 57],[1, 4, 61],[2, 3, 100],[3, 5, 34],[4, 5, 13],
]
这里 u,v,w 的含义以及顺序应根据具体题目具体分析,这里的设定是(u, v, w)表示一条边从u节点指向v节点,权重为w。
// 添加边:
public static void addEdge(int u, int v, int w) {next[cnt] = head[u];to[cnt] = v;weight[cnt] = w;head[u] = cnt;++cnt;
}
下面我们图解一下,在链式前向星中,依次添加6条边到有向图中的逻辑。

如果看不懂,建议返回上面去看各个数组的下标以及值的含义。
添加边 {1, 6, 2}
head[1] = 1:节点1的第一条边的编号是1。next[1] = 0:边1没有下一条边。to[1] = 2:边1的终点是节点2。weight[1] = 6:边1的权重是6。cnt:2,表示当前边的数量是1,下一条边的编号是2。
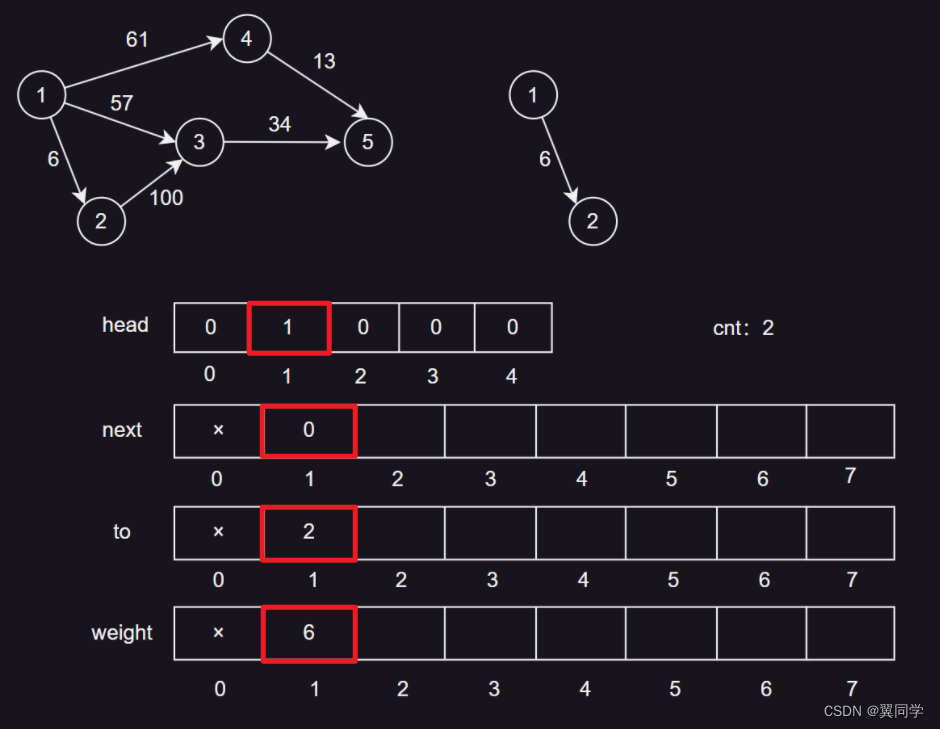
添加边 {1, 3, 57}
head[1] = 2:节点1的第一条边的编号是2。next[2] = 1:边2的下一条边是边1。to[2] = 3:边2的终点是节点3。weight[2] = 57:边2的权重是57。cnt:3,表示当前边的数量是2,下一条边的编号是3。
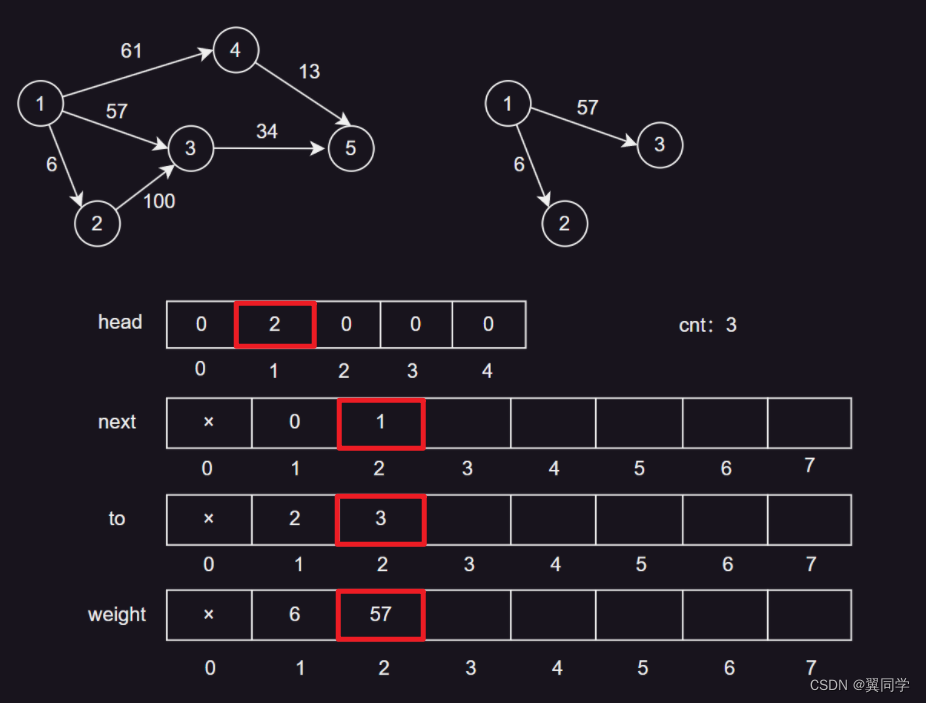
添加边 {1, 4, 61}
head[1] = 3:节点1的第一条边的编号是3。next[3] = 2:边3的下一条边是边2。to[3] = 4:边3的终点是节点4。weight[3] = 61:边3的权重是61。cnt:4,表示当前边的数量是3,下一条边的编号是4。
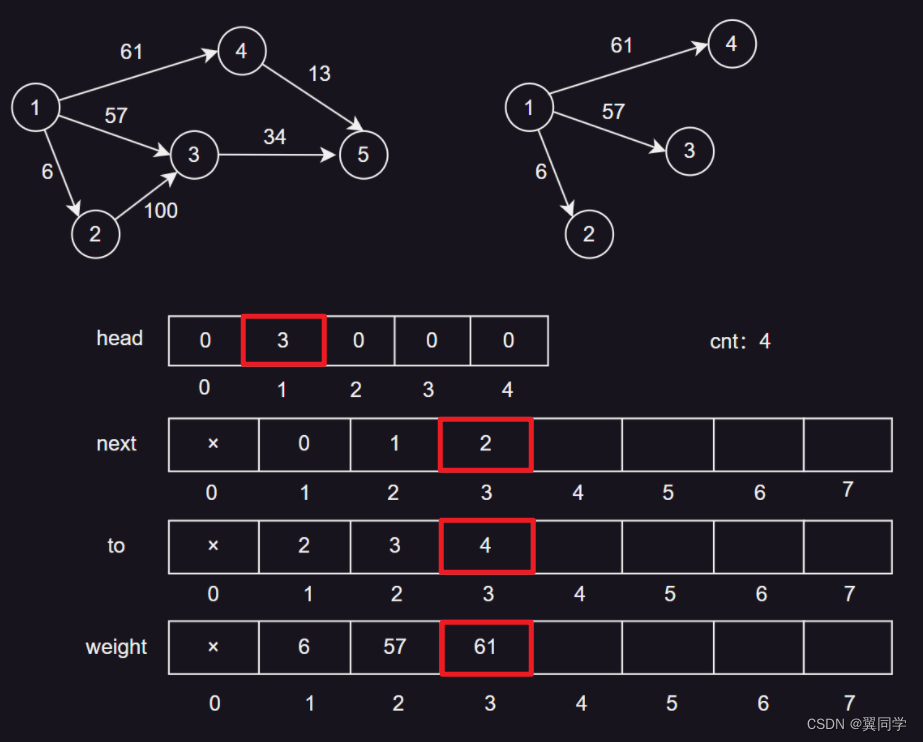
添加边 {2, 3, 100}
head[2] = 4:节点2的第一条边的编号是4。next[4] = 0:边4没有下一条边。to[4] = 3:边4的终点是节点3。weight[4] = 100:边4的权重是100。cnt:5,表示当前边的数量是4,下一条边的编号是5。
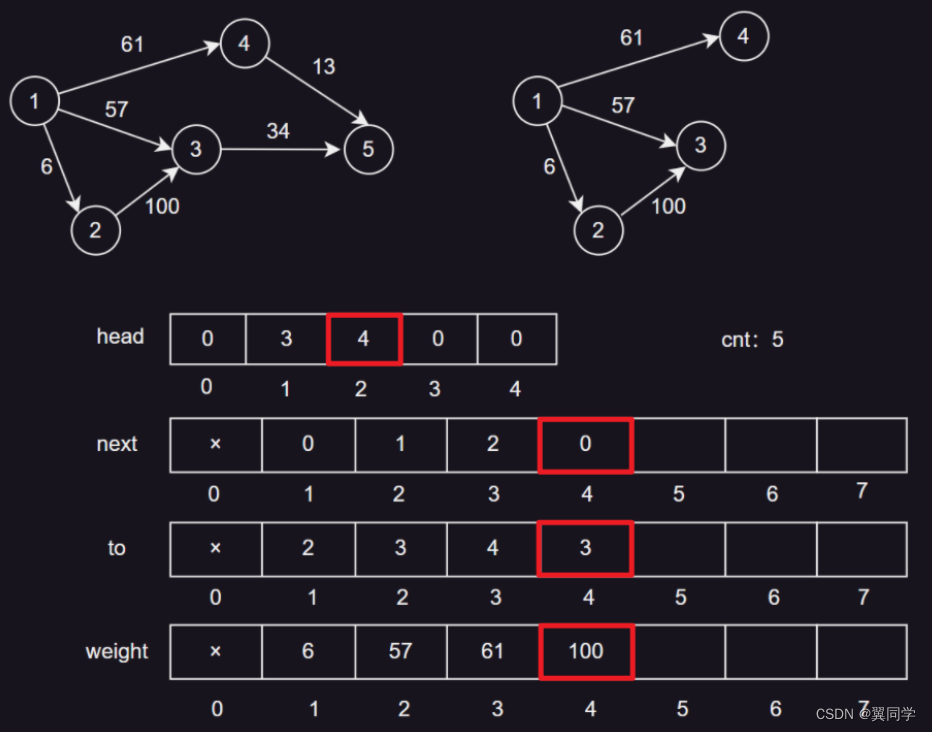
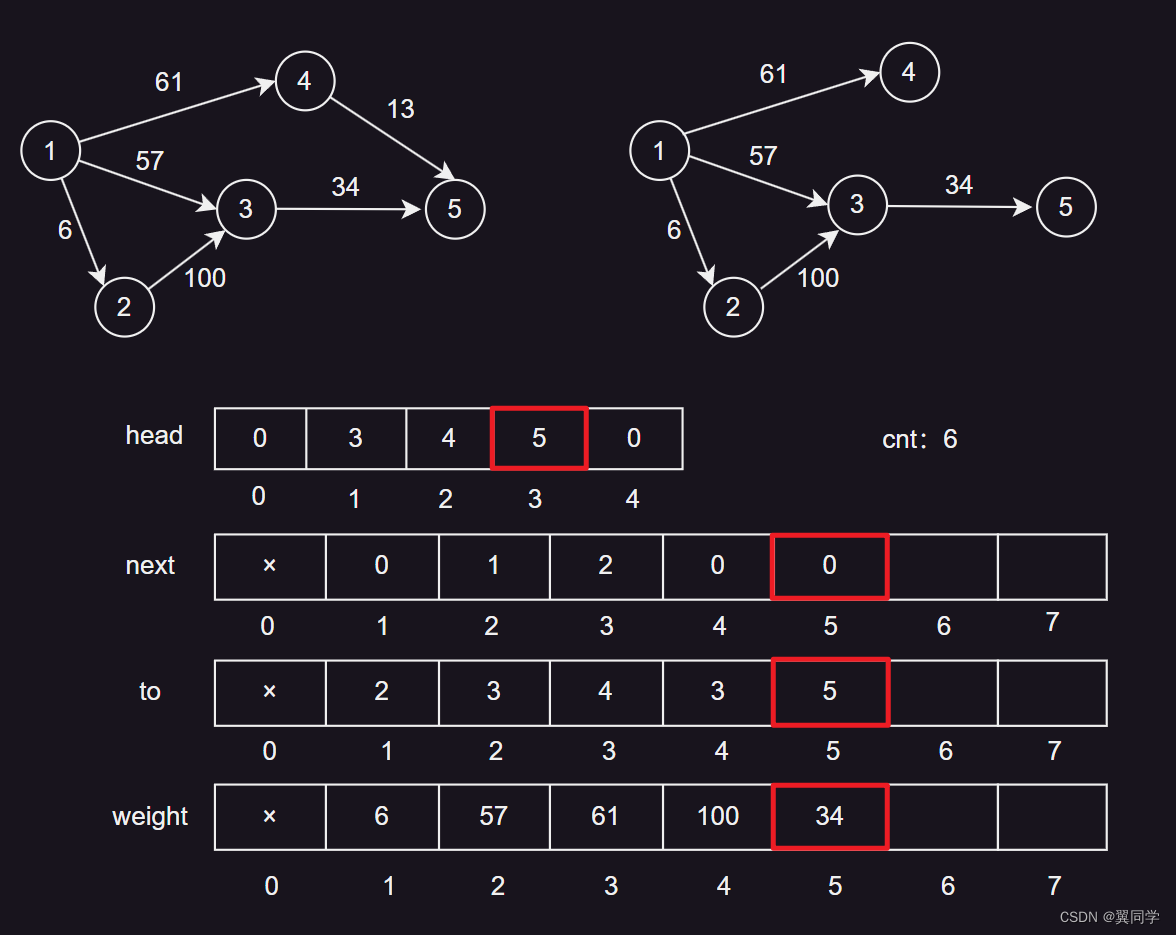
添加边 {3, 5, 34}
head[3] = 5:节点3的第一条边的编号是5。next[5] = 0:边5没有下一条边。to[5] = 5:边5的终点是节点5。weight[5] = 34:边5的权重是34。cnt:6,表示当前边的数量是5,下一条边的编号是6。
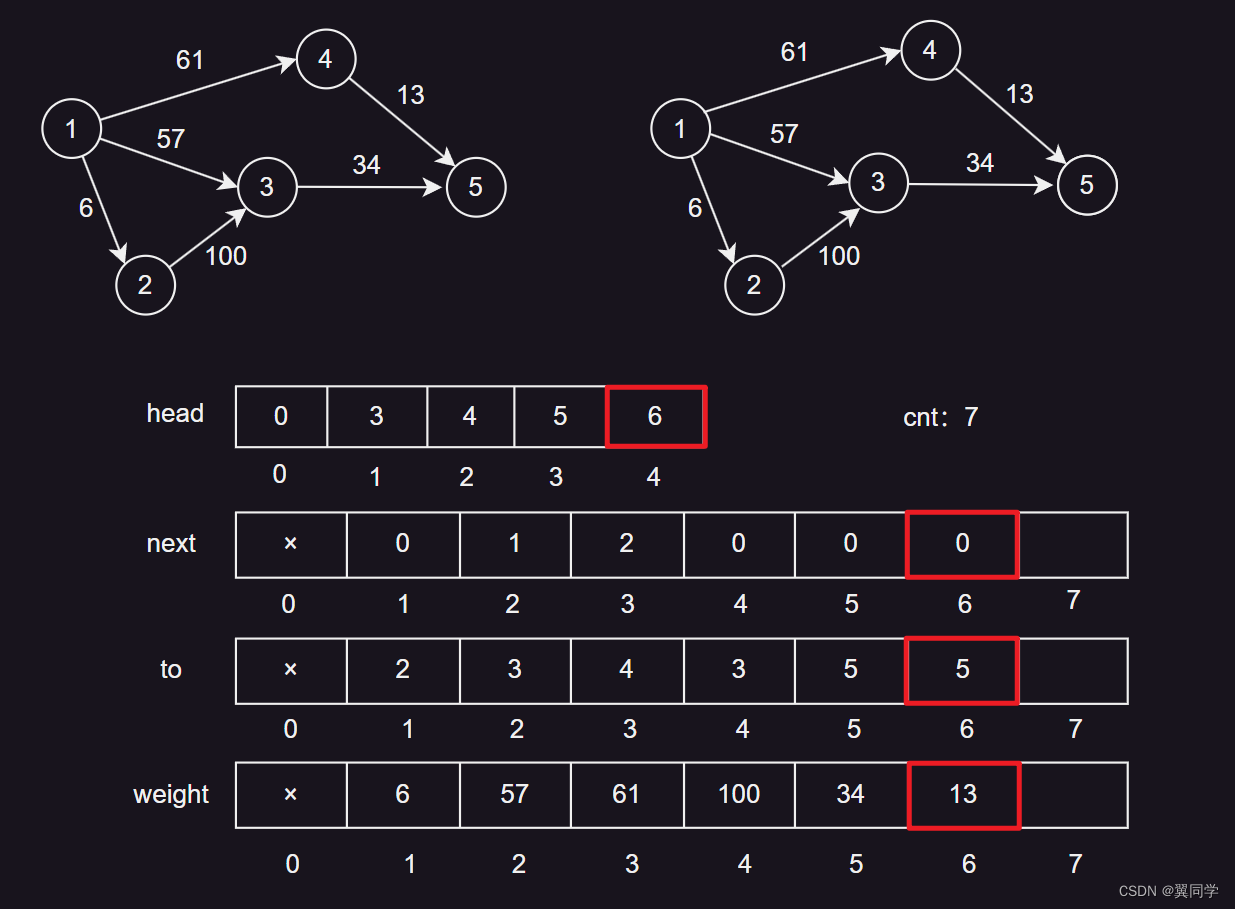
添加边 {4, 5, 13}
head[4] = 6:节点4的第一条边的编号是6。next[6] = 0:边6没有下一条边。to[6] = 5:边6的终点是节点5。weight[6] = 13:边6的权重是13。cnt:7,表示当前边的数量是6,下一条边的编号是7。
七、遍历图
遍历图的逻辑也不难理解,就是对于每个节点,遍历其所有的邻居,根据next数组不断去拿到和每个节点连接的边的编号,直到没有邻居节点为止,一步步跳着找嘛。
步骤如下:
- 对于每个节点,通过
head数组找到该节点的第一条边。 - 通过
next数组找到下一条边,直到next数组的值为0,表示没有更多的边。 - 在遍历过程中,可以通过
to和weight数组获取边的终点和权重。
我们用打印邻居节点的方式来验证遍历的结果:
public static void traversal(int n) {StringBuilder sb = new StringBuilder();sb.append("链式前向星遍历,u: (v, w)表示u有一条边前往v,权重为w\n");for (int i = 1; i <= n; i++) {sb.append("[").append(i).append("]: ");for (int ei = head[i]; ei > 0; ei = next[ei]) {sb.append("(").append(to[ei]).append(",").append(weight[ei]).append(") "); // 输出边的终点和权重}sb.append("\n");}System.out.println(sb.toString()); // 打印结果
}
八、完整代码
package cn.zhengyiyi;import java.util.Arrays;public class Main {public static int N = 11;public static int M = 21; /*** 编号为 i 的节点,其第一条边的编号为 head[i]* 备注:如果 head[i] 为0,说明没有一条边从节点 i 出发*/public static int[] head = new int[N];/*** 编号为 i 的边,它的下一条边是 next[i],*/public static int[] next = new int[M];/*** 编号为 i 的边,前往的节点是 to[i],也就是第 i 条边的终点是 to[i]*/public static int[] to = new int[M];/*** 编号为 i 的边,权重是 weight[i]*/public static int[] weight = new int[M];/*** 记录边的数量,初始时值为 1*/public static int cnt;// 初始化链式前向星public static void build(int n) {cnt = 1; // 边从1开始编号Arrays.fill(head, 1, n + 1, 0); // head[1 ... n] 全设为 0}// 添加一条边:(u->v,权重为w)public static void addEdge(int u, int v, int w) {// 1. 更新next数组,将新边的next置为旧的头边号head[u],方便后续跳到旧的头边号next[cnt] = head[u];// 2. 更新to数组,设置当前新边的终点为vto[cnt] = v; // 3. 更新weight数组,设置当前边的权重wweight[cnt] = w;// 4. 更新head数组,将原先的头边号修改为当前新边head[u] = cnt;// 5. 最后边的编号要自增++cnt;}// 建立有向图public static void directGraph(int[][] edges) {for (int[] edge : edges) {addEdge(edge[0], edge[1], edge[2]); // 添加有向边}}// 建立无向图public static void undirectGraph(int[][] edges) {for (int[] edge : edges) {addEdge(edge[0], edge[1], edge[2]); // 添加边addEdge(edge[1], edge[0], edge[2]); // 无向图需要添加反向边}}// 遍历图public static void traversal(int n) {StringBuilder sb = new StringBuilder();sb.append("链式前向星遍历,u: (v, w)表示u有一条边前往v,权重为w\n");for (int i = 1; i <= n; i++) {sb.append("[").append(i).append("]: ");for (int ei = head[i]; ei > 0; ei = next[ei]) {sb.append("(").append(to[ei]).append(",").append(weight[ei]).append(") "); // 输出边的终点和权重}sb.append("\n");}System.out.println(sb.toString()); // 打印结果}public static void main(String[] args) {int n = 5; // 节点数build(n); // 初始化int[][] directEdges = { // 有向图的边{ 1, 6, 2 },{ 1, 3, 57 },{ 1, 4, 61 },{ 2, 3, 100 },{ 3, 5, 34 },{ 4, 5, 13 }};directGraph(directEdges); // 建立有向图traversal(n); // 遍历有向图}
}
运行结果:
链式前向星遍历,u: (v, w)表示u有一条边前往v,权重为w
[1]: (4,61) (3,57) (6,2)
[2]: (3,100)
[3]: (5,34)
[4]: (5,13)
[5]:
相关文章:

【数据结构 | 图论】如何用链式前向星存图(保姆级教程,详细图解+完整代码)
一、概述 链式前向星是一种用于存储图的数据结构,特别适合于存储稀疏图,它可以有效地存储图的边和节点信息,以及边的权重。 它的主要思想是将每个节点的所有出边存储在一起,通过数组的方式连接(类似静态数组实现链表…...
气象预测新篇章:Python人工智能的变革力量
Python是功能强大、免费、开源,实现面向对象的编程语言,在数据处理、科学计算、数学建模、数据挖掘和数据可视化方面具备优异的性能,这些优势使得Python在气象、海洋、地理、气候、水文和生态等地学领域的科研和工程项目中得到广泛应用。可以…...
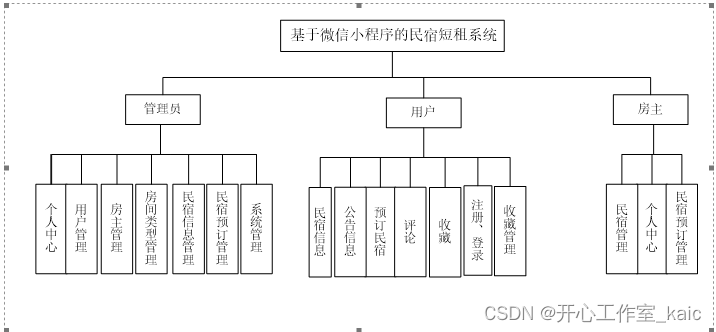
基于微信小程序的民宿短租系统设计与实现(论文+源码)_kaic
摘 要 随着社会的发展,出差、旅游成为常态,也就造成民宿短租市场的兴起。人们新到陌生的环境里找民宿一般都是通过中介。中介虽然可以快速找到合适的民宿但会收取大量的中介费用,这对刚到新环境里的人们来说是一笔大的资金支出。也有一些人通…...
vue3开发前端表单缓存自定义指令,移动端h5必备插件
开发背景 公司需要开发一款移动端应用,使用vue开发,用户录入表单需要本地缓存,刷新页面,或者不小心关掉重新进来,上次录入的信息还要存在。 这里有两种方案,第一种就是像博客平台一样,实时保存…...
骗子查询系统源码
源码简介 小权云黑管理系统 V1.0 功能如下: 1.添加骗子,查询骗子 2.可添加团队后台方便审核用 3.在线反馈留言系统 4.前台提交骗子,后台需要审核才能过 5.后台使用光年UI界面 6.新增导航列表,可给网站添加导航友链 7.可添加云黑类…...

目标检测+车道线识别+追踪
一种方法: 车道线检测-canny边缘检测-霍夫变换 一、什么是霍夫变换 霍夫变换(Hough Transform)是一种在图像处理和计算机视觉中广泛使用的特征检测技术,主要用于识别图像中的几何形状,尤其是直线、圆和椭圆等常见形状…...
非wpf应用程序项目【类库、用户控件库】中使用HandyControl
文章速览 前言参考文章实现方法1、添加HandyControl包;2、添加资源字典3、修改资源字典内容 坚持记录实属不易,希望友善多金的码友能够随手点一个赞。 共同创建氛围更加良好的开发者社区! 谢谢~ 前言 wpf应用程序中,在入口项目中…...
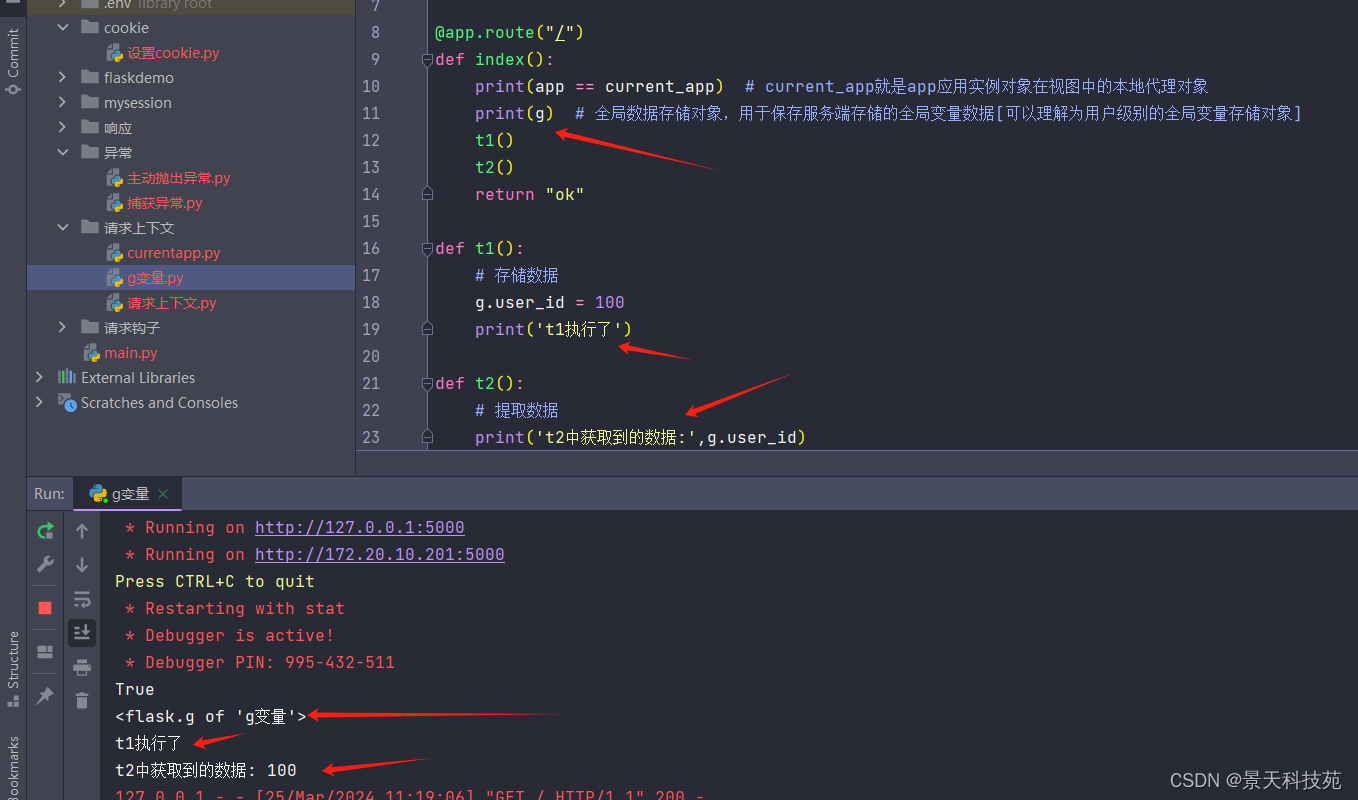
【python】flask执行上下文context,请求上下文和应用上下文原理解析
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...
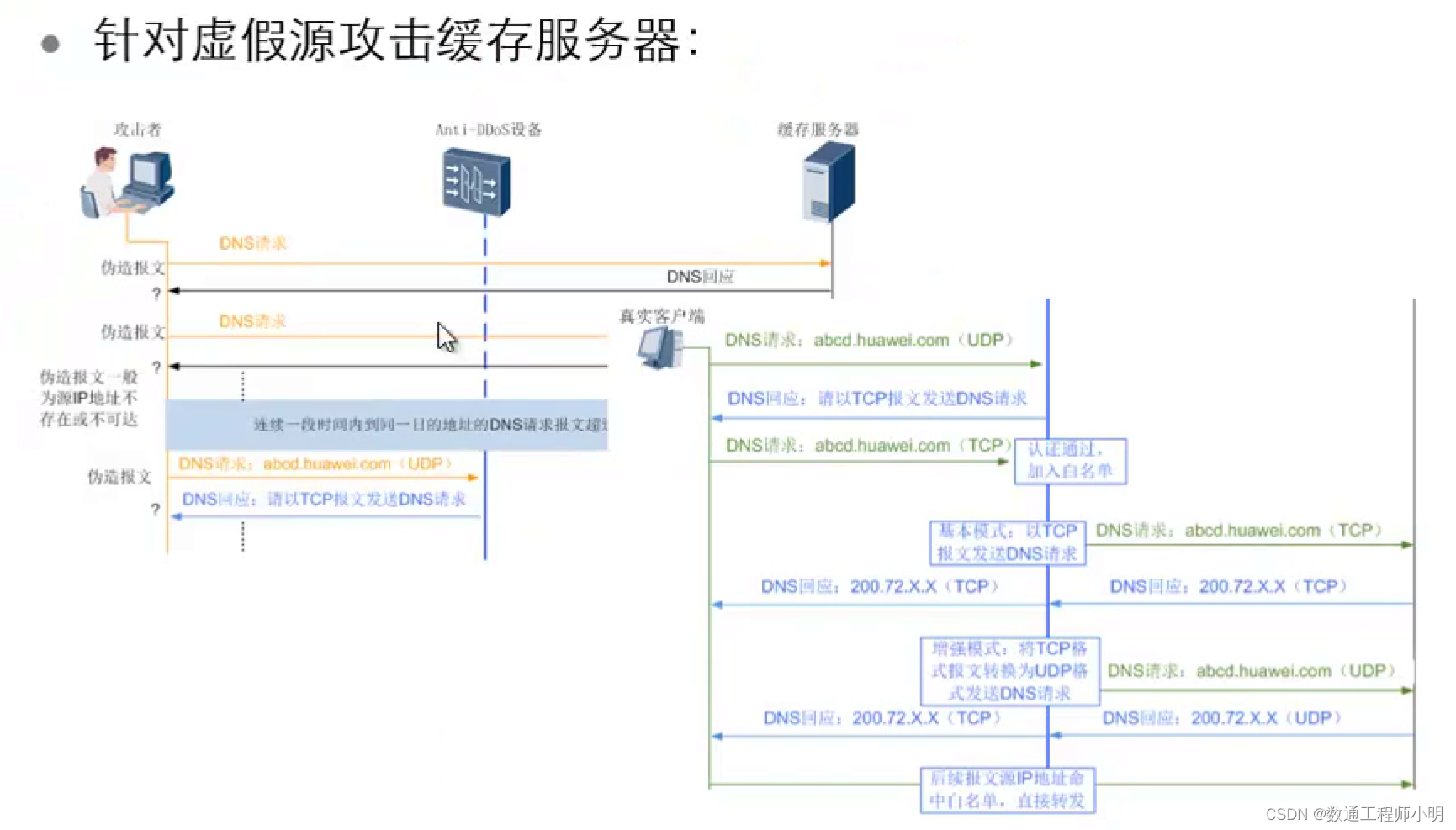
DDos系列攻击原理与防御原理
七层防御体系 静态过滤 命中黑名单 对确定是攻击的流量直接加入黑名单(源地址命中黑名单直接丢弃,缺乏机动性和扩展性) 畸形报文过滤 畸形报文攻击 TCP包含多个标记位,排列组合有规律 • 现象:TCP标记位全为1 …...
Python拆分PDF、Python合并PDF
WPS能拆分合并,但却是要输入编辑密码,我没有。故写了个脚本来做拆分,顺便附上合并的代码。 代码如下(extract.py) #!/usr/bin/env python """PDF拆分脚本(需要Python3.10)Usage::$ python extract.py <pdf-fil…...
经典总结大全-技巧总结-数据开发-基本函数-常识整理-经典面试题)
SqlServer(4)经典总结大全-技巧总结-数据开发-基本函数-常识整理-经典面试题
六、技巧 1、11,12的使用,在SQL语句组合时用的较多 “where 11” 是表示选择全部 “where 12”全部不选, 如: if strWhere !‘’ begin set strSQL ‘select count(*) as Total from [’ tblName ] where ’ strWhere …...
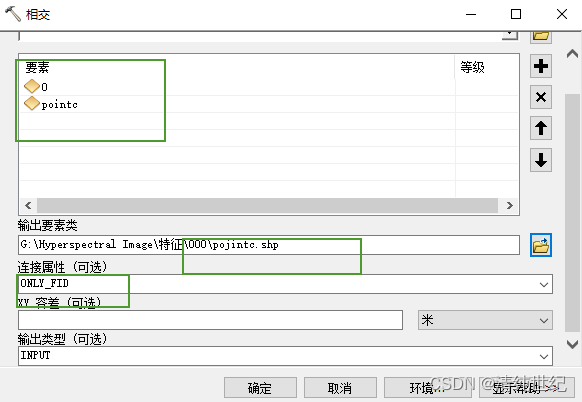
ArcGIS矢量裁剪矢量
一、利用相交工具 Arctoolbox工具一分析工具一叠加分析一相交...

pygame用chatgpt绘制3d沿x轴旋转的
import pygame from pygame.locals import * import sys import mathpygame.init()width, height 800, 600 screen pygame.display.set_mode((width, height))vertices [(0, 100, 0), (100, 200, 0), (300, 100, 0)]angle 0 rotation_speed 2 # 可根据需要调整旋转速度 c…...

golang大小写规则的影响
目录 golang大小写的规则: 1、可见性(visibility): 2、包的导入和调用: 3、json序列化和反序列化: 4、结构体字段的导出和可见性: 5、方法和函数的导出和可见性 : 6、常量和变…...
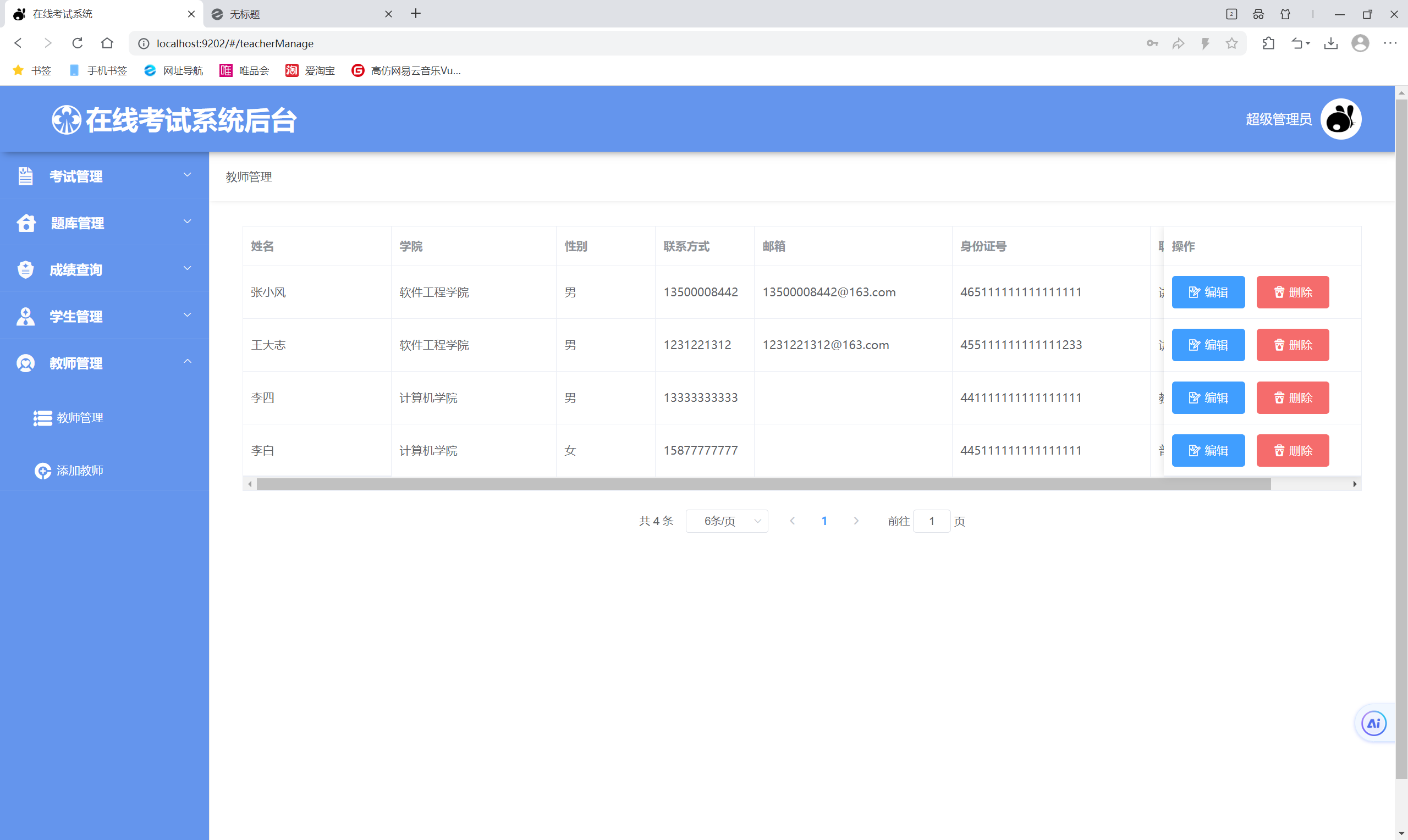
基于Java在线考试系统系统设计与实现(源码+部署文档)
博主介绍: ✌至今服务客户已经1000、专注于Java技术领域、项目定制、技术答疑、开发工具、毕业项目实战 ✌ 🍅 文末获取源码联系 🍅 👇🏻 精彩专栏 推荐订阅 👇🏻 不然下次找不到 Java项目精品实…...

如何应对复杂软件工程的开发流程?
应对复杂软件工程的开发流程通常需要一个结构化和系统化的方法。这种方法不仅包括采用合适的技术和工具,还涉及到项目管理、团队协作、需求分析、设计、实施、测试、部署和维护等多个方面。以下是一些关键步骤,以及如何将这些步骤应用于使用LabVIEW进行软…...

JAVA的NIO和BIO底层原理分析
文章目录 一、操作系统底层IO原理1. 简介2. 操作系统进行IO的流程 二、BIO底层原理1. 什么是Socket2. JDK原生编程的BIO 三、Java原生编程的NIO1. 简介2. NIO和BIO的主要区别3. Reactor模式4. NIO的三大核心组件5. NIO核心源码分析 一、操作系统底层IO原理 1. 简介 IO&#x…...
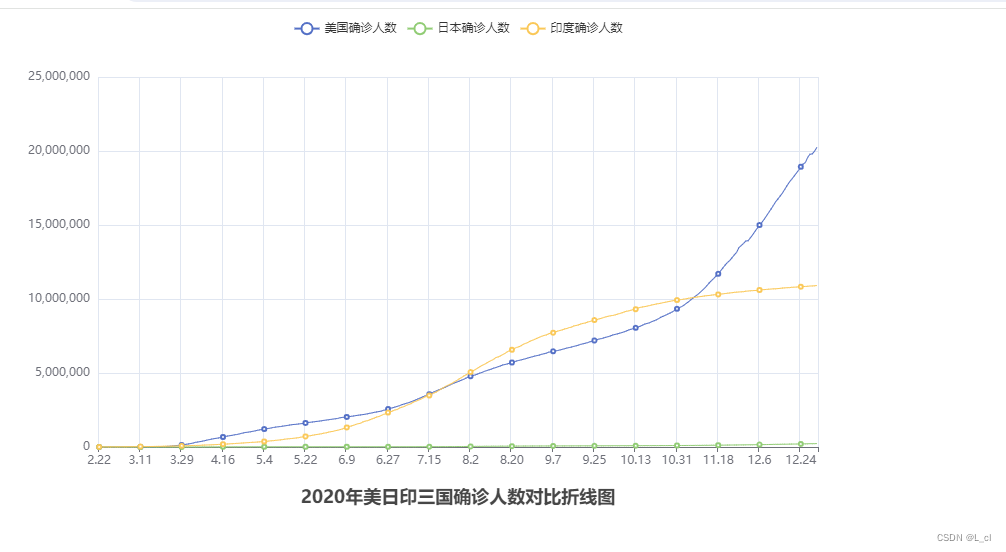
Python学习从0到1 day18 Python可视化基础综合案例 1.折线图
我默记这段路的酸楚,等来年春暖花开之时再赏心阅读 —— 24.3.24 python基础综合案例 数据可视化 — 折线图可视化 一、折线图案例 1.json数据格式 2.pyecharts模块介绍 3.pyecharts快速入门 4.数据处理 5.创建折线图 1.json数据格式 1.什么是json 2.掌握如何使用js…...

HTML网站的概念
目录 前言: 1.什么是网页: 2.什么是网站: 示例: 3.服务器: 总结: 前言: HTML也称Hyper Text Markup Language,意思是超文本标记语言,同时HTML也是前端的基础&…...

【微服务】Nacos(配置中心)
文章目录 1.AP和CP1.基本介绍2.说明 2.Nacos配置中心实例1.架构图2.在Nacos Server加入配置1.配置列表,加号2.加入配置3.点击发布,然后返回4.还可以编辑 3. 创建 Nacos 配置客户端模块获取配置中心信息1.创建子模块 e-commerce-nacos-config-client50002…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...
