算法打卡day28|贪心算法篇02|Leetcode 122.买卖股票的最佳时机 II、55. 跳跃游戏、45.跳跃游戏 II
算法题
Leetcode 122.买卖股票的最佳时机 II
题目链接:122.买卖股票的最佳时机 II
大佬视频讲解:买卖股票的最佳时机 II视频讲解
个人思路
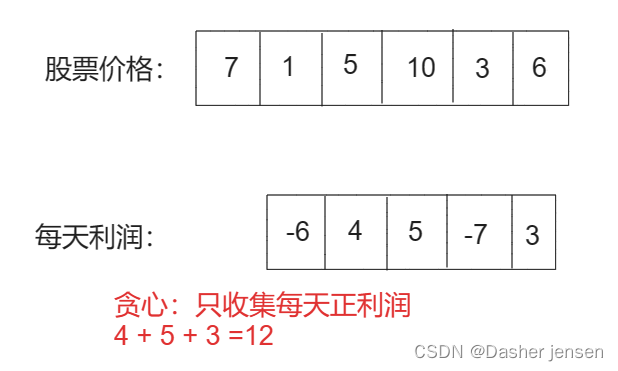
因为只有一只股票,且两天作一个交易单元,那每次只收集正利润就可以最终最多可以获取的利润,可以用贪心。
解法
贪心法
从下图可以发现,其实收集每天的正利润就可以,收集正利润的区间,就是股票买卖的区间,而且只需要关注最终利润,不需要记录区间。
局部最优:收集每天的正利润,全局最优:求得最大利润
class Solution {public int maxProfit(int[] prices) {int result = 0;//最终利润for (int i = 1; i < prices.length; i++) {result += Math.max(prices[i] - prices[i - 1], 0);//只收集正利润}return result;}
}时间复杂度:O(n);(遍历整个数组)
空间复杂度:O(1);(常量级的变量)
Leetcode 55. 跳跃游戏
题目链接:55. 跳跃游戏
大佬视频讲解:跳跃游戏视频讲解
个人思路
可以每次取最大的跳跃步数,这个就是可以跳跃的覆盖范围,当覆盖范围盖过终点 就代表能跳到终点。每步取最优,最后推出全局最优,用贪心。
解法
贪心法
这个问题转化为跳跃覆盖范围究竟可不可以覆盖到终点!
每次移动取最大跳跃步数(得到最大的覆盖范围),每移动一个单位,就更新最大覆盖范围。
贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点。

i 每次移动只能在 cover 的范围内移动,每移动一个元素,cover 得到该元素数值(新的覆盖范围)的补充,让 i 继续移动下去。而 cover 每次只取 max;如果 cover 大于等于了终点下标,直接 return true 。
class Solution {public boolean canJump(int[] nums) {if (nums.length == 1) {return true;}int coverRange = 0; //覆盖范围, 初始覆盖范围应该是0,因为下面的迭代是从下标0开始的//在覆盖范围内更新最大的覆盖范围for (int i = 0; i <= coverRange; i++) {coverRange = Math.max(coverRange, i + nums[i]);if (coverRange >= nums.length - 1) {//找到覆盖终点return true;}}return false;}
}时间复杂度:O(n);(遍历整个数组)
空间复杂度:O(1);(常量级的变量)
Leetcode 45.跳跃游戏 II
题目链接:45.跳跃游戏 II
大佬视频讲解:跳跃游戏 II视频讲解
个人思路
这道题和上一题思路类似;只是本题要计算最少步数。在计算时,当前可移动距离尽可能多走,如果还没到终点,步数再加一。一步尽可能多走,从而达到最少步数。局部可以推全局,用贪心。
解法
贪心法
在解题时要注意,不能真的能跳多远就跳多远,那样就不知道下一步最远能跳到哪里了。
要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最少步数.
所以这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖。
如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点.

class Solution {public int jump(int[] nums) {int result = 0;//步数int end = 0;// 当前覆盖的最远距离下标int temp = 0;// 下一步覆盖的最远距离下标//移动下标i只要遇到当前覆盖最远距离的下标,直接步数加一for (int i = 0; i <= end && end < nums.length - 1; ++i) {temp = Math.max(temp, i + nums[i]);//更新最大覆盖范围if (i == end) {// 可达位置的改变次数就是跳跃次数end = temp;result++;}}return result;}
}时间复杂度:O(n);(遍历整个数组)
空间复杂度:O(1);(常量级变量)
以上是个人的思考反思与总结,若只想根据系列题刷,参考卡哥的网址代码随想录算法官网
相关文章:

算法打卡day28|贪心算法篇02|Leetcode 122.买卖股票的最佳时机 II、55. 跳跃游戏、45.跳跃游戏 II
算法题 Leetcode 122.买卖股票的最佳时机 II 题目链接:122.买卖股票的最佳时机 II 大佬视频讲解:买卖股票的最佳时机 II视频讲解 个人思路 因为只有一只股票,且两天作一个交易单元,那每次只收集正利润就可以最终最多可以获取的利润…...

2013年认证杯SPSSPRO杯数学建模A题(第一阶段)护岸框架全过程文档及程序
2013年认证杯SPSSPRO杯数学建模 A题 护岸框架 原题再现: 在江河中,堤岸、江心洲的迎水区域被水流长期冲刷侵蚀。在河道整治工程中,需要在受侵蚀严重的部位设置一些人工设施,以减弱水流的冲刷,促进该处泥沙的淤积&…...

【3】3道链表力扣题:删除链表中的节点、反转链表、判断一个链表是否有环
3道链表力扣题 一、删除链表中的节点🌏 题目链接📕 示例🍀 分析💻 代码 二、反转链表🌏 题目链接📕 示例🍀 分析① 递归② 迭代 三、判断一个链表是否有环🌏 题目链接📕 …...
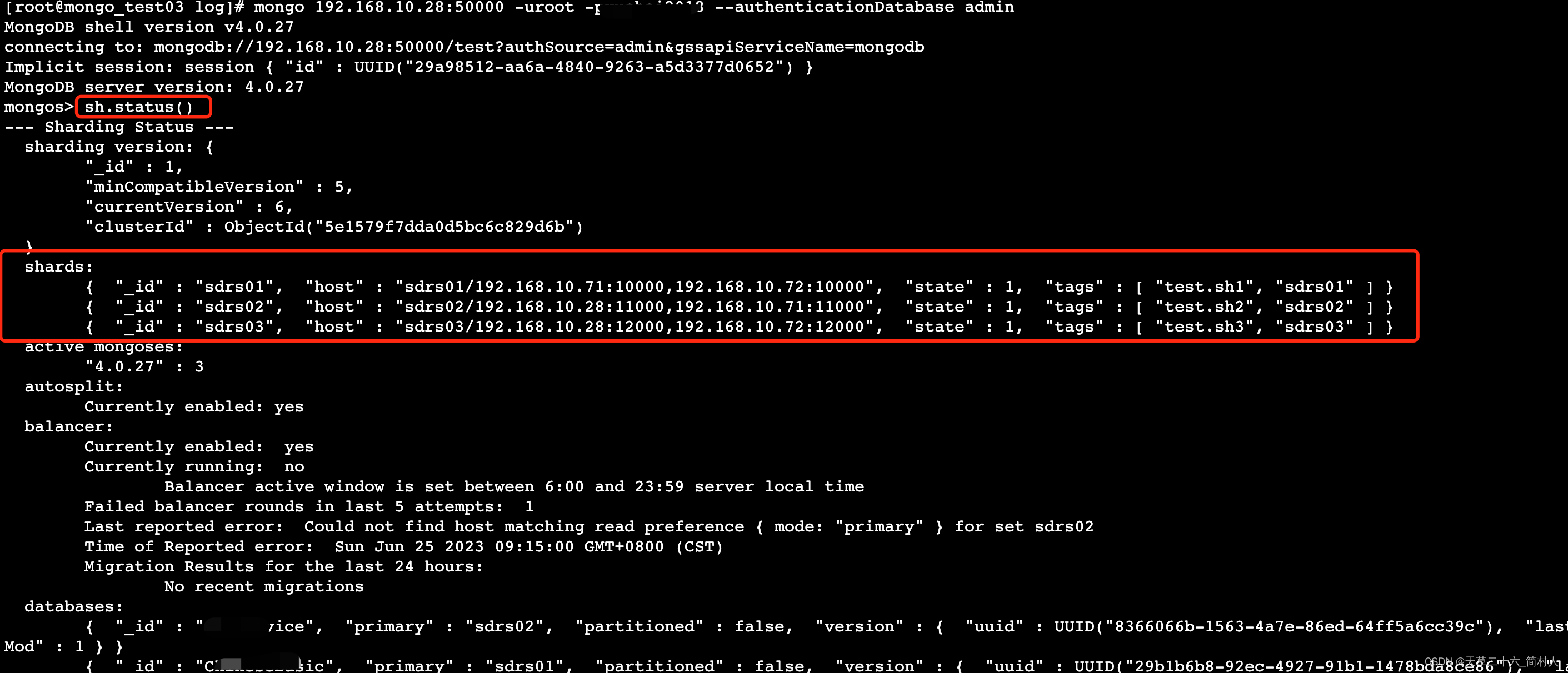
mongodb sharding分片模式的集群数据库,日志治理缺失导致写入数据库报错MongoWriteConcernException的问题总结(上)
一、背景 常见的mongodb集群模式有以下三种: 主从复制(Master-Slave)模式副本集(Replica Set)模式分片(Sharding)模式 公司测试环境搭建的集群采用分片模式,有同事反馈说…...

苹果Mac OS系统上安装brew
1.命令行安装brew Homebrew是 mac的包管理器,仅需执行相应的命令,就能下载安装需要的软件包,可以省掉自己去下载、解压、拖拽(安装)等繁琐的步骤。 a. 打开HomeBrew官网:https://brew.sh/index.html b. 点击页面上的复制按钮,打…...

应用侧渲染流程
应用侧渲染流程 《Android应用程序UI硬件加速渲染环境初始化过程分析》 https://blog.csdn.net/Luoshengyang/article/details/45769759 《Android HWUI绘制流程》 https://wizzie.top/android/android_HWUI_Draw/#1-gpu%E6%B8%B2%E6%9F%93%E7%A1%AC%E4%BB%B6%E5%8A%A0%E9%…...

学生党开放式运动耳机怎么选?五款超高销量高性价比品牌推荐
开放式运动耳机成为了许多人的运动首选装备,想要在众多的开放式耳机中找到一款价格亲民,且性能在线高性价比的开放式运动耳机可并非那么简单,所以今天我就来为大家推荐五款超高销量、高性价比的运动耳机品牌。 在推荐之前,整理了…...
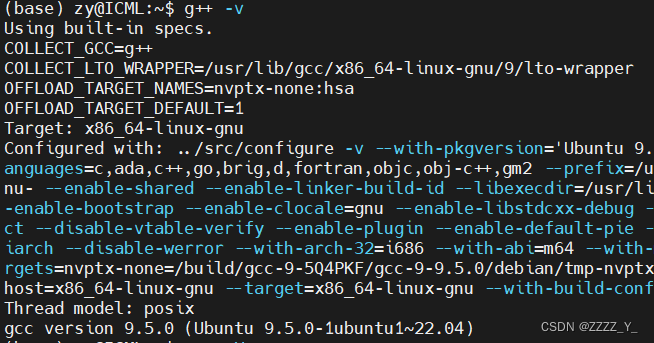
服务器中有g++,但是查询不到,Command ‘g++‘ not found
有gcc但是查询不到g,gcc版本为9.5.0 (base) zyICML:~$ g -V Command g not found, but can be installed with: apt install g Please ask your administrator. 突然就出现这个问题,导致detectron装不上,现在有时间了专门研究下怎么解决 这…...
,split() ,sys.stdin.readline() ,matrix.append, input().strip())
count(“0“),split() ,sys.stdin.readline() ,matrix.append, input().strip()
目录 count() 方法主要用于计算一个序列(例如列表、元组或字符串)中某个元素出现的次数...
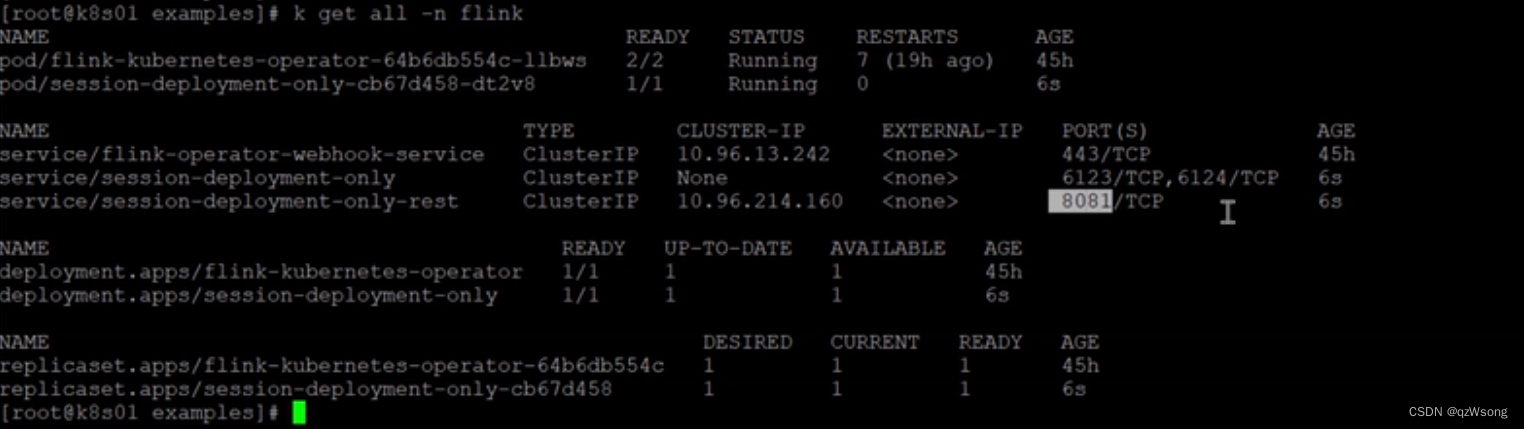
Flink on Kubernetes (flink-operator) 部署Flink
flink on k8s 官网 https://nightlies.apache.org/flink/flink-kubernetes-operator-docs-release-1.1/docs/try-flink-kubernetes-operator/quick-start/ 我的部署脚本和官网不一样,有些地方官网不够详细 部署k8s集群 注意,按照默认配置至少有两台wo…...

代码随想录算法训练营第三十二天|122.买卖股票的最佳时机II、55. 跳跃游戏、45.跳跃游戏II
122.买卖股票的最佳时机II - 🔗 讲解 - 🔗 方法一: 💡这道题自己想到的办法没有解析那么清晰,大致思路就是第一步先找到第一个可以买进的时间(也就是第一个prices[i] < prices[i 1]的i)&…...

常见数据库分类介绍及其适用场景
一、引言 数据库是指在计算机系统中,为了结构化地管理和存储数据而建立起来的一种数据管理系统。它以高效、安全和可靠的方式存储和管理用户所需的各种数据,并提供了强大的数据处理和查询功能。随着信息技术的不断发展,数据库已经成为现代计…...
)
周末总结(2024/03/30)
工作 接受破烂现状,改变状态 上周一周的工作都感觉是摸鱼状态,每天只有三个小时左右的时间聚焦在工作上,其他时间都在胡思乱想。但是我发现可以在工作中学习和下班相关的技术栈。我无意改变自己的工作状态,只想在5月底找好下家然后…...
爬楼梯)
(75)爬楼梯
文章目录 1. 每日一言2. 题目2.1 解题思路2.1.1 递归2.1.2 记忆化搜索2.1.3 动态规划2.1.4 动态规划空间优化 2.2 代码2.2.1 递归2.2.2 记忆化搜索2.2.3 动态规划2.2.4 动态规划空间优化 3. 结语 1. 每日一言 Happy life lies in a peaceful mind. 幸福的生活存在于心绪的宁静…...
ttkbootstrap界面美化系列之Notebook(四)
在简单的界面设计中,Notebook也是常用的组件之一,Notebook组件的引入可以根据标签来切换不同的界面。使得界面更有层次感,不必都挤在一个界面上。在tkinter中就有Notebook组件,在ttkbootstrap中,同样也对Notebook进行了…...

MySQL8存储过程整合springboot
注意:调用使用mybatis-plus3形式调用,可能会有些区别 1. 创建存储过程 -- -- 生成员工工号的存储过程 DELIMITER $$ CREATE PROCEDURE generate_employee_number(OUT employeeNumber VARCHAR(20)) -- 解释 out 一个返回值 BEGINDECLARE prefix VARCHAR…...

Acwing 1238.日志统计 双指针
小明维护着一个程序员论坛。现在他收集了一份”点赞”日志,日志共有 N� 行。 其中每一行的格式是: ts id 表示在 ts 时刻编号 id 的帖子收到一个”赞”。 现在小明想统计有哪些帖子曾经是”热帖”。 如果一个帖子曾在任意一个长度为 D 的…...

Matlab-R2022b-安装文件分享
一、MATLAB主要特点和功能 MATLAB是一款强大的科学计算软件,专门用于算法开发、数据分析、数值计算以及科学数据可视化。 以下是一些MATLAB的主要特点和功能: 1.矩阵运算: MATLAB的名字来源于"Matrix Laboratory"(矩阵实验室&…...

Flutter开发之objectbox
Flutter开发之objectbox 在之前进行iOS开发的时候使用WCDB去进行管理数据库很方便,它支持ORM(Object-Relational Mapping,对象关系映射),用于实现面向对象编程语言里不同类型系统的数据之间的转换。 那么在Flutter开发…...
)
AI Drug Discovery Design(学习路线)
AIDD,即AI Drug Discovery & Design,是近年来非常火热的技术应用,已经介入到新药设计到研发的大部分环节当中,为新药发现与开发带来了极大的助力。其学习路线涉及多个学科和领域的知识。以下是一个可能的AIDD学习路线…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
