math模块篇(七)
文章目录
- math.dist(p, q)
- math.hypot(*coordinates)
- math.sin(x)
- math.tan(x)
- math.degrees(x)
- math.radians(x)
- math.acosh(x)
- math.asinh(x)
- math.atanh(x)
math.dist(p, q)
在Python的math模块中,并没有一个名为math.dist(p, q)的函数。可能你是想要计算两点p和q之间的距离,但这通常不是通过math模块直接完成的。在二维或三维空间中,两点之间的距离可以通过欧几里得距离公式来计算。
对于二维空间中的两点p(x1, y1)和q(x2, y2),它们之间的欧几里得距离d可以通过以下公式计算:
²)
和q(x2, y2, z2),距离d可以通过以下公式计算:
- y1)² + (z2 - z1)²)
,你可以使用math.sqrt和math.pow函数来实现这些计算。下面```是一个计算二维空间中两点距离的示例:
import mathdef calculate_distance(p, q):x1, y1 = px2, y2 = qreturn math.sqrt(math.pow(x2 - x1, 2) + math.pow(y2 - y1, 2))# 示例用法
p = (1, 2)
q = (4, 6)
distance = calculate_distance(p, q)
print(distance) # 输出两点之间的距离
如果你正在处理更高维度的空间或者想要使用更高效的数值计算库,你可能会考虑使用numpy或scipy这样的库,它们提供了更强大的数组操作和数学函数。例如,使用numpy计算二维空间中两点之间的距离可以这样写:
import numpy as npp = np.array([1, 2])
q = np.array([4, 6])
distance = np.linalg.norm(q - p)
print(distance) # 输出两点之间的距离
在这个例子中,np.linalg.norm函数计算了向量q - p的欧几里得范数,也就是两点之间的距离。
math.hypot(*coordinates)
math.hypot(*coordinates) 是 Python 标准库 math 模块中的一个函数,它用于计算给定坐标值的欧几里得范数(Euclidean norm),也就是直角三角形的斜边长度。该函数接受任意数量的参数,每个参数代表一个坐标值,并返回这些坐标值构成的向量的长度。
在数学上,欧几里得范数是通过计算坐标值的平方和然后取平方根来得到的。对于 N 维空间中的点 (x1, x2, …, xN),其欧几里得范数(或长度)定义为:
norm = sqrt(x1^2 + x2^2 + ... + xN^2)
math.hypot 函数就是用来高效计算这个值的。它使用了一种算法,可以避免逐个计算平方和平方根,从而提高了计算效率。
下面是一些使用 math.hypot 的例子:
二维空间中的点
import mathx = 3
y = 4
hypotenuse = math.hypot(x, y)
print(hypotenuse) # 输出 5.0,因为 sqrt(3^2 + 4^2) = sqrt(9 + 16) = sqrt(25) = 5
三维空间中的点
import mathx = 1
y = 2
z = 3
hypotenuse = math.hypot(x, y, z)
print(hypotenuse) # 输出 3.7416573867739413,因为 sqrt(1^2 + 2^2 + 3^2) = sqrt(1 + 4 + 9) = sqrt(14) ≈ 3.7416573867739413
更高维度的空间
你可以传递任意数量的参数给 math.hypot,它都可以计算对应的高维空间中点的欧几里得范数。
import mathx1, x2, x3, x4 = 1, 2, 3, 4
hypotenuse = math.hypot(x1, x2, x3, x4)
print(hypotenuse) # 输出 5.477225575051661,因为 sqrt(1^2 + 2^2 + 3^2 + 4^2) = sqrt(1 + 4 + 9 + 16) = sqrt(30) ≈ 5.477225575051661
总之,math.hypot 函数是一个非常实用的工具,用于计算欧几里得空间中点的向量长度。
math.sin(x)
math.sin(x) 是 Python 中 math 模块的一个函数,用于计算给定角度 x 的正弦值。这里的 x 应该是一个以弧度为单位的角,而不是度。
在 Python 中使用 math.sin(x) 之前,你需要先导入 math 模块。以下是一个简单的示例:
import math# 计算45度(弧度制表示)的正弦值
x_in_degrees = 45
x_in_radians = math.radians(x_in_degrees) # 将角度转换为弧度sin_value = math.sin(x_in_radians)
print(sin_value) # 输出正弦值
注意,math.sin() 函数接受的是弧度制的角度,而不是度数。如果你有一个度数值并希望计算其正弦值,你需要使用 math.radians() 函数将其转换为弧度。
对于上述代码,输出将接近于 0.7071067811865476,这是 45 度(在弧度制下表示为 math.pi / 4)的正弦值。
如果你需要处理复数或者矩阵中的元素,你可能需要使用 numpy 库中的 numpy.sin() 函数,它支持数组和矩阵操作,并且对于复数也有效。例如:
import numpy as np# 计算45度(弧度制表示)的正弦值
x_in_degrees = 45
x_in_radians = np.radians(x_in_degrees) # 将角度转换为弧度sin_value = np.sin(x_in_radians)
print(sin_value) # 输出正弦值
在这种情况下,sin_value 将是一个标量值,因为我们只对单个角度进行了操作。但是,如果 x_in_radians 是一个 numpy 数组,np.sin() 将会对数组中的每个元素进行正弦计算。
math.tan(x)
math.tan(x) 是 Python 中 math 模块的一个函数,用于计算给定角度 x 的正切值。与 math.sin(x) 和 math.cos(x) 类似,这里的 x 应该是一个以弧度为单位的角,而不是度。
在使用 math.tan(x) 之前,你也需要先导入 math 模块。下面是一个简单的示例:
import math# 计算45度(弧度制表示)的正切值
x_in_degrees = 45
x_in_radians = math.radians(x_in_degrees) # 将角度转换为弧度tan_value = math.tan(x_in_radians)
print(tan_value) # 输出正切值
输出将接近于 1.0,这是 45 度(在弧度制下表示为 math.pi / 4)的正切值。
请注意,math.tan(x) 的结果可能是无穷大(对于 (2k+1) * math.pi / 2 的 x 值,其中 k 是整数),或者是未定义(对于 k * math.pi 的 x 值)。这是因为正切函数在这些点上不存在或无穷大。
对于需要处理复数或者数组中的元素的情况,你可以使用 numpy 库中的 numpy.tan() 函数,如下所示:
import numpy as np# 计算45度(弧度制表示)的正切值
x_in_degrees = 45
x_in_radians = np.radians(x_in_degrees) # 将角度转换为弧度tan_value = np.tan(x_in_radians)
print(tan_value) # 输出正切值
在这个例子中,tan_value 将是一个标量值,因为我们只对单个角度进行了操作。如果 x_in_radians 是一个 numpy 数组,np.tan() 将会对数组中的每个元素计算正切值。
math.degrees(x)
math.degrees(x) 是 Python 中 math 模块的一个函数,它用于将弧度转换为度数。x 参数应该是一个以弧度为单位的角,函数将返回对应的以度数为单位的角。
这里是一个简单的例子,展示了如何使用 math.degrees() 函数:
import math# 假设我们有一个以弧度为单位的角
radians = math.pi / 4# 将弧度转换为度数
degrees = math.degrees(radians)print(degrees) # 输出 45.0
在这个例子中,我们有一个以弧度为单位的角(即 π/4,它等于 45 度),我们使用 math.degrees() 函数将其转换为度数,并打印出结果,输出将是 45.0。
这个函数在处理三角函数时特别有用,尤其是当你需要在度数和弧度之间转换时。例如,你可能使用 math.radians() 来将角度转换为弧度,然后使用 math.sin(), math.cos(), math.tan() 等函数进行计算,最后使用 math.degrees() 将结果转换回度数。
math.radians(x)
math.radians(x) 是 Python 中 math 模块的一个函数,用于将角度 x 从度数转换为弧度。当你在使用三角函数(如 math.sin(), math.cos(), math.tan() 等)时,这些函数期望的输入是以弧度为单位的,而不是以度数为单位。因此,如果你有一个以度数为单位的角,并且想要计算它的三角函数值,你需要先使用 math.radians() 将它转换为弧度。
下面是一个简单的例子,展示了如何使用 math.radians() 函数:
import math# 假设我们有一个以度数为单位的角
degrees = 45# 将度数转换为弧度
radians = math.radians(degrees)print(radians) # 输出转换后的弧度值
输出将是 0.7853981633974483,这是 45 度转换为弧度的结果。
在编写涉及三角函数的代码时,始终记住输入到这些函数中的角度应该是以弧度为单位的。如果你有一个以度数为单位的角,使用 math.radians() 进行转换是一个好习惯,这样可以避免计算错误。
下面是一个更完整的例子,它计算了一个以度数为单位的角的正弦值:
import math# 假设我们有一个以度数为单位的角
degrees = 45# 将度数转换为弧度
radians = math.radians(degrees)# 计算正弦值
sin_value = math.sin(radians)print(sin_value) # 输出正弦值
在这个例子中,我们首先使用 math.radians() 将角度从度数转换为弧度,然后使用 math.sin() 计算转换后的角的正弦值。
math.acosh(x)
math.acosh(x) 是 Python 中 math 模块的一个函数,用于计算给定数值 x 的反双曲余弦值(也称为双曲余弦的逆函数)。反双曲余弦函数是双曲余弦函数 math.cosh(x) 的逆运算。
双曲余弦函数 cosh(x) 定义为 (exp(x) + exp(-x)) / 2,其中 exp(x) 是自然指数函数。反双曲余弦函数 acosh(x) 则满足 cosh(acosh(x)) = x。
math.acosh(x) 的输入 x 必须大于或等于 1,因为双曲余弦函数 cosh(x) 在 x >= 0 的范围内是增函数,并且 cosh(0) = 1。因此,acosh(x) 的定义域为 [1, +∞)。
以下是一个使用 math.acosh() 的示例:
import math# 计算反双曲余弦值
x = 2
acosh_value = math.acosh(x)print(acosh_value) # 输出反双曲余弦值
输出将是 acosh(2) 的值,它大于 0 但小于 math.pi,因为 cosh(math.pi/2) = math.sqrt(2)。
需要注意的是,math.acosh() 只接受单个数值作为输入,并且返回单个数值作为输出。如果你需要处理数组或矩阵中的元素,你可能需要使用像 numpy 这样的科学计算库,它提供了 numpy.arccosh() 函数来处理多维数组。
例如,使用 numpy 计算反双曲余弦值:
import numpy as np# 计算数组元素的反双曲余弦值
x = np.array([1, 2, 3])
acosh_values = np.arccosh(x)print(acosh_values) # 输出数组元素的反双曲余弦值
这将输出一个数组,包含每个对应元素的反双曲余弦值。
math.asinh(x)
math.asinh(x) 是 Python 中 math 模块的一个函数,用于计算给定数值 x 的反双曲正弦值(也称为双曲正弦的逆函数)。反双曲正弦函数是双曲正弦函数 math.asinh(x) 或 math.sinh(x) 的逆运算。
双曲正弦函数 sinh(x) 定义为 (exp(x) - exp(-x)) / 2,其中 exp(x) 是自然指数函数。反双曲正弦函数 asinh(x) 则满足 sinh(asinh(x)) = x。
math.asinh(x) 的输入 x 可以是任何实数,包括负数。它的值域为整个实数轴,即 (-∞, +∞)。
以下是一个使用 math.asinh() 的示例:
import math# 计算反双曲正弦值
x = 0.5
asinh_value = math.asinh(x)print(asinh_value) # 输出反双曲正弦值
输出将是 0.5 的反双曲正弦值,它位于 0 和 math.pi/2 之间。
同样地,如果你需要处理数组或矩阵中的元素,你可以使用 numpy 库的 numpy.arcsinh() 函数。例如:
import numpy as np# 计算数组元素的反双曲正弦值
x = np.array([0, 0.5, 1])
asinh_values = np.arcsinh(x)print(asinh_values) # 输出数组元素的反双曲正弦值
这将输出一个数组,包含每个对应元素的反双曲正弦值。
math.atanh(x)
math.atanh(x) 是 Python 中 math 模块的一个函数,用于计算给定数值 x 的反双曲正切值(也称为双曲正切的逆函数)。反双曲正切函数是双曲正切函数 math.tanh(x) 的逆运算。
双曲正切函数 tanh(x) 定义为 (exp(x) - exp(-x)) / (exp(x) + exp(-x)),其中 exp(x) 是自然指数函数。反双曲正切函数 atanh(x) 则满足 tanh(atanh(x)) = x。
math.atanh(x) 的输入 x 必须在 -1 和 1 之间(包括 -1 和 1),因为 tanh(x) 的值域是 [-1, 1]。因此,atanh(x) 的定义域为 [-1, 1]。
以下是一个使用 math.atanh() 的示例:
import math# 计算反双曲正切值
x = 0.5
atanh_value = math.atanh(x)print(atanh_value) # 输出反双曲正切值
输出将是 0.5 的反双曲正切值,它位于 0 和 math.pi/2 之间。
同样地,如果你需要处理数组或矩阵中的元素,你可以使用 numpy 库的 numpy.arctanh() 函数。例如:
import numpy as np# 计算数组元素的反双曲正切值
x = np.array([-0.5, 0, 0.5])
atanh_values = np.arctanh(x)print(atanh_values) # 输出数组元素的反双曲正切值
这将输出一个数组,包含每个对应元素的反双曲正切值。
请注意,math.atanh() 只接受单个数值作为输入,并且返回单个数值作为输出。如果你需要处理向量或矩阵,使用 numpy 会更加方便和高效。
相关文章:
)
math模块篇(七)
文章目录 math.dist(p, q)math.hypot(*coordinates)math.sin(x)math.tan(x)math.degrees(x)math.radians(x)math.acosh(x)math.asinh(x)math.atanh(x) math.dist(p, q) 在Python的math模块中,并没有一个名为math.dist(p, q)的函数。可能你是想要计算两点p和q之间的…...

wordpress插件,免费的wordpress插件
WordPress作为世界上最受欢迎的内容管理系统之一,拥有庞大的插件生态系统,为用户提供了丰富的功能扩展。在内容创作和SEO优化方面,有一类特殊的插件是自动生成原创文章并自动发布到WordPress站点的工具。这些插件能够帮助用户节省时间和精力&…...

Remote Desktop Manager for Mac:远程桌面管理软件
Remote Desktop Manager for Mac,是远程桌面管理的理想之选。它集成了多种远程连接技术,无论是SSH、RDP还是VNC,都能轻松应对,让您随时随地安全访问远程服务器和工作站。 软件下载:Remote Desktop Manager for Mac下载…...

如何撰写研究论文
SEVENTYFOUR/SHUTTERSTOCK 即使对于有经验的作家来说,将数月或数年的研究浓缩到几页纸中也是一项艰巨的任务。作者需要在令人信服地解决他们的科学问题和详细地呈现他们的结果之间找到最佳平衡点,以至于丢失了关键信息。他们必须简明扼要地描述他们的方…...
数据结构
一、栈 先进后出 二、队列 先进先出 三、数组 查询快,增加修改慢 四、链表 查询慢,增加修改慢 五、二叉树 节点: 查找二叉树 二叉查找树的特点 二叉查找树,又称二叉排序树或者二叉搜索树 每一个节点上最多有两个子节点 左子树上所…...
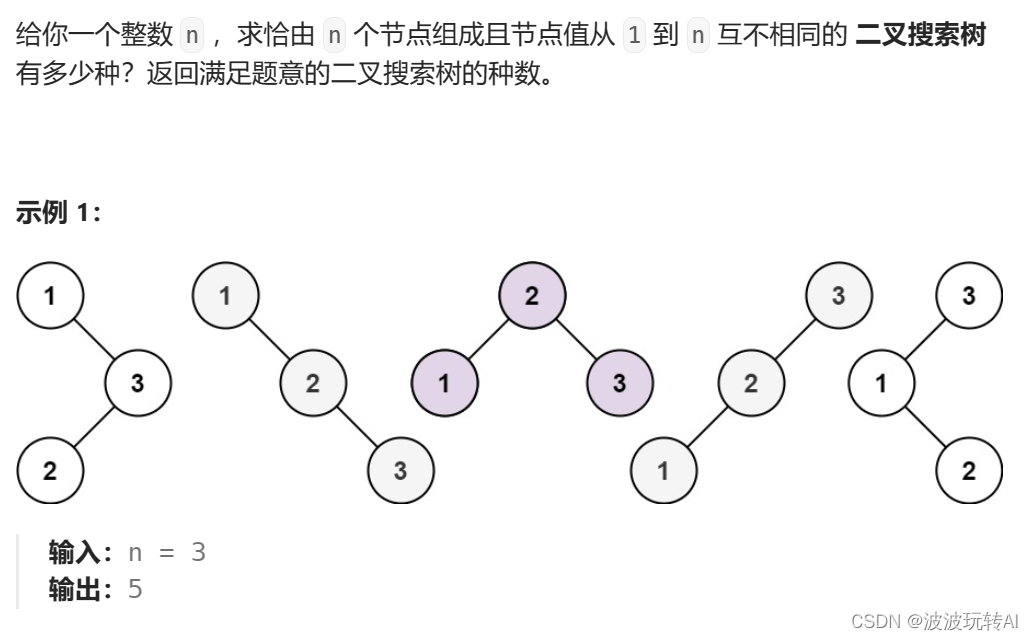
动态规划相关题目
文章目录 1.动态规划理论基础2.斐波那契数3.爬楼梯4.使用最小花费爬楼梯5.不同路径6.不同路径 II7. 整数拆分8. 不同的二叉搜索树 1.动态规划理论基础 1.1 什么是动态规划? 动态规划,英文:Dynamic Programming,简称DP,如果某一…...

iOS - Runtime - Class-方法缓存(cache_t)
文章目录 iOS - Runtime - Class-方法缓存(cache_t)1. 散列表的存取值 iOS - Runtime - Class-方法缓存(cache_t) Class内部结构中有个方法缓存(cache_t),用散列表(哈希表)来缓存曾经调用过的方法,可以提高…...

2014年认证杯SPSSPRO杯数学建模B题(第一阶段)位图的处理算法全过程文档及程序
2014年认证杯SPSSPRO杯数学建模 B题 位图的处理算法 原题再现: 图形(或图像)在计算机里主要有两种存储和表示方法。矢量图是使用点、直线或多边形等基于数学方程的几何对象来描述图形,位图则使用像素来描述图像。一般来说&#…...

【物联网项目】基于ESP8266的家庭灯光与火情智能监测系统——文末完整工程资料源码
目录 系统介绍 硬件配置 硬件连接图 系统分析与总体设计 系统硬件设计 ESP8266 WIFI开发板 人体红外传感器模块 光敏电阻传感器模块 火焰传感器模块 可燃气体传感器模块 温湿度传感器模块 OLED显示屏模块 系统软件设计 温湿度检测模块 报警模块 OLED显示模块 …...

Unity中控制帧率的思考
如何控制帧率: 在Unity中,你可以通过设置Application.targetFrameRate来限制帧率。 例如,如果你想将帧率限制为16帧, 你可以在你的代码中添加以下行: Application.targetFrameRate 16; 通常,这行代码会放在…...

阿里云子域名配置,且不带端口访问
进入阿里云控制台,创建一个SSL证书 # 域名名称child.domain.com创建完成后,将返回主机记录以及记录值,保存好,用于下一步使用 创建DNS解析 创建DNS的TXT类型解析 选择记录类型:TXT 填写主机记录:_dnsa…...

C#-ConcurrentDictionary用于多线程并发字典
ConcurrentDictionary 是 .NET Framework 中用于多线程并发操作的一种线程安全的字典集合类。它提供了一种在多个线程同时访问和修改字典时保持数据一致性的机制。 以下是 ConcurrentDictionary 类的一些重要特性和用法: 线程安全性:ConcurrentDictiona…...

深入探讨多线程编程:从0-1为您解释多线程(下)
文章目录 6. 死锁6.1 死锁原因 6.2 避免死锁的方法加锁顺序一致性。超时机制。死锁检测和解除机制。 6. 死锁 6.1 死锁 原因 系统资源的竞争:(产生环路)当系统中供多个进程共享的资源数量不足以满足进程的需要时,会引起进程对2…...
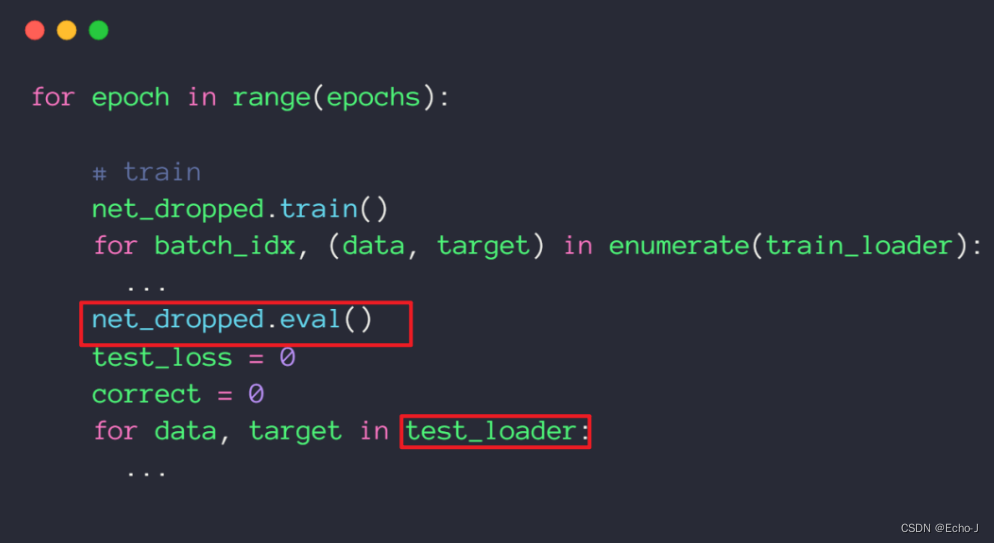
深度学习pytorch——减少过拟合的几种方法(持续更新)
1、增加数据集 2、正则化(Regularization) 正则化:得到一个更加简单的模型的方法。 以一个多项式为例: 随着最高次的增加,会得到一个更加复杂模型,模型越复杂就会更好的拟合输入数据的模型(图-1)&#…...

排序第五篇 归并排序
一 简介 归并排序(Merge Sort) 的基本思想是: 首先将待排序文件看成 n n n 个长度为1的有序子文件, 把这些子文件两两归并, 得到 n 2 \frac{n}{2} 2n 个长度为 2 的有序子文件; 然后再把这 n 2 \frac{n}{2} 2n 个有序的子…...
【Win】使用PowerShell和Webhooks轻松发送消息至Microsoft Teams
Microsoft Teams是一款由微软开发的团队协作和通讯工具。如果您对这个名字还不太熟悉,那么现在就是一个了解它的好时机。微软将Teams定位为其之前Skype for Business解决方案的继任者,并且它也提供了与其他基于频道的通讯应用程序(例如Slack、…...

ESCTF-OSINT赛题WP
这你做不出来?check ESCTF{湖北大学_嘉会园食堂} 这个识图可以发现是 淡水渔人码头 但是 osint 你要发现所有信息 聊天记录说国外 同时 提示给了美国 你综合搜索 美国 渔人码头 在美国旧金山的渔人码头(英语:Fisherman’s Wharf)是一个著名旅…...

2024蓝桥杯省赛保奖突击班-Day2-前缀和、差分、尺取_笔记_练习题解
3月25日-课堂笔记 前缀和预处理 O ( n ) \mathcal{O}(n) O(n) s[1] a[1]; for(int i 2; i < n; i)s[i] s[i - 1] a[i];利用前缀和查询区间和 O ( 1 ) O(1) O(1) long long calc(int l, int r) {return l 1 ? s[r] : s[r] - s[l - 1]; }差分序列的求法 c[1] a[…...

C++基础之虚函数(十七)
一.什么是多态 多态是在有继承关系的类中,调用同一个指令(函数),不同对象会有不同行为。 二.什么是虚函数 概念:首先虚函数是存在于类的成员函数中,通过virtual关键字修饰的成员函数叫虚函数。 性质&am…...

快速入门Kotlin①基本语法
前言 23年底读了一遍“Kotlin官方文档”,官方文档大而全,阅读下来,大有裨益。 此系列文章的目的是记录学习进程,同时,若能让读者迅速掌握重点内容并快速上手,那就再好不过了。 函数 带有两个 Int 参数、…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...

Qt学习及使用_第1部分_认识Qt---Qt开发基本流程
前言 学以致用,通过QT框架的学习,一边实践,一边探索编程的方方面面. 参考书:<Qt 6 C开发指南>(以下称"本书") 标识说明:概念用粗体倾斜.重点内容用(加粗黑体)---重点内容(红字)---重点内容(加粗红字), 本书原话内容用深蓝色标识,比较重要的内容用加粗倾…...
