算法之美:堆排序原理剖析及应用案例分解实现
这段时间持续更新关于“二叉树”的专栏文章,关心的小伙伴们对于二叉树的基本原理已经有了初步的了解。接下来,我将会更深入地探究二叉树的原理,并且展示如何将这些原理应用到更广泛的场景中去。文章将延续前面文章的风格,尽量精炼明了,减少冗长的废话,旨在简洁清晰地阐述二叉树的原理及其应用。让我们一起深入了解,并探索其潜在的价值吧!
什么是堆排序
指利用堆这种数据结构所设计的一种排序算法,将二叉堆的数据进行排序,构建一个有序的序列。在这排序过程中,只需要个别【临时存储】空间,所以堆排序是原地排序算法,空间复杂度为O(1)。
本身大顶堆和小顶堆里面的元素是无序的,只是有一定的规则在里面:
1)大顶堆,每个父节点的值都大于或等于其子节点的值,即根节点的值最大;
2)小顶堆,每个父节点的值都小于或等于其子节点的值,即根节点的值最小;

堆排序流程
把无序数组构建成二叉堆,建堆结束后,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换(删除操作), 堆顶a[1]与最后一个元素a[n]交换,最大元素放到下标为n的位置, 末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆(堆化操作),这样会得到n个元素的次小值
反复执行上述步骤,得到一个有序的数组。
综上所述,这个堆排序的过程其实可以直接分为建堆和排序两大步骤:
1)【建堆】过程的时间复杂度为O(n),排序过程的时间复杂度为O(nlogn),所以 堆排序整体的时间复杂度为O(nlogn);
2)【堆排序】不是稳定的算法,在排序的过程中,将堆最后一个节点跟堆顶节点互换,可能改变值相同数据的原始相对顺序;
堆排序动画演示:Heap Sort Visualization (usfca.edu)
堆排序实现
public class HeapSort {/*** 从小到大进行堆排序* @param source*/public static void sort(int[] source) {//步骤一:构建堆,数组下标0不存储数据int[] heap = new int[source.length + 1];//根据待排序数组,构造一个无序的堆System.arraycopy(source, 0, heap, 1, source.length);//对堆中的元素做下沉调整,从长度的一半处开始,往堆顶索引1处扫描)//二叉堆特性:数组索引一半后的都是叶子节点,不需要做下沉,一半前都是非叶子节点,才需要做for (int i = (heap.length) / 2; i > 0; i--) {down(heap, i, heap.length - 1);}System.out.println("大顶堆:"+Arrays.toString(heap));// 步骤二:堆排序}/*** 比较大小,item[left] 元素是否小于 item[right]的元素*/private static boolean rightBig(int[] heap, int left, int right) {return heap[left] < heap[right];}/*** 交互堆中两个元素的位置*/private static void swap(int[] heap, int i, int j) {int temp = heap[i];heap[i] = heap[j];heap[j] = temp;}/*** 使用下沉操作,堆顶和最后一个元素交换后,重新堆化* 不断比较 节点 arr[k]和对应 左节点arr[2*k] 和 右节点arr[2*k+1]的大小,如果当前结点小,则需要交换位置* 直到找到 最后一个索引节点比较完成 则结束* <p>* 数组中下标为 k 的节点* 左子节点下标为 2*k 的节点* 右子节点就是下标 为 2*k+1 的节点* 父节点就是下标为 k/2 取整的节点*/private static void down(int[] heap, int k, int range) {// 最后一个节点的下标是range,即元素总个数while (2 * k <= range) {//记录当前节点的左右子节点,较大的节点int maxIndex;if (2 * k + 1 <= range) {if (rightBig(heap, 2 * k, 2 * k + 1)) {maxIndex = 2 * k + 1;} else {maxIndex = 2 * k;}} else {maxIndex = 2 * k;}//比较当前节点和较大接的值,如果当前节点大则结束if (heap[k] > heap[maxIndex]) {break;} else {//否则往下一层比较,当前节点的k变为子节点中较大的值swap(heap, k, maxIndex);k = maxIndex;}}}/*** 从小到大进行堆排序* @param source*/public static void sort(int[] source) {//步骤一:构建堆,数组下标0不存储数据int[] heap = new int[source.length + 1];//根据待排序数组,构造一个无序的堆System.arraycopy(source, 0, heap, 1, source.length);//对堆中的元素做下沉调整,从长度的一半处开始,往堆顶索引1处扫描)//二叉堆特性:数组索引一半后的都是叶子节点,不需要做下沉,一半前都是非叶子节点,才需要做for (int i = (heap.length) / 2; i > 0; i--) {down(heap, i, heap.length - 1);}System.out.println("大顶堆:"+Arrays.toString(heap));// 步骤二:堆排序,把堆顶元素和数组最后一个索引元素交换;然后再堆化,然后堆顶又是最大元素,再和数组倒数第二索引处交换;持续进行直到最后// 类似删除操作,只需要下沉操作重新堆化即可//记录未排序的元素中最大的索引int maxUnSortIndex = heap.length - 1;//通过循环,交换堆顶元素和最大未排序元素的下标while (maxUnSortIndex != 1) {//交换元素swap(heap, 1, maxUnSortIndex);//排序后最大元素所在的索引,不要参与堆的下沉,所以 递减1maxUnSortIndex--;//继续对堆顶处的元素进行下沉调整down(heap, 1, maxUnSortIndex);}//把heap中的数据复制到原数组source中System.arraycopy(heap, 1, source, 0, source.length);}//Main入口public static void main(String[] args) {//待排序数组int[] arr = {923,23,12,4,9932,11,34,49,123,222,880};//堆排序HeapSort.sort(arr);//输出排序后数组中的元素System.out.println("堆排序:"+Arrays.toString(arr));}}海量数据之堆应用TopK思想
从一堆数据中选出前多少个最大或最小数
堆典型问题,思路方案:取大用小,取小用大
取最大的K个数用小顶堆,取最小的K个数用大顶堆;
取海量数据里面最小的K个数
要找出数组中最小的k个数,就要【构造一个有k个元素的大顶堆】,大顶堆的堆顶元素值最大,比较堆顶的元素和扫描的元素,如果堆顶元素 < 扫描元素,继续扫描其他元素。如果堆顶元素 > 扫描元素 ,将堆顶元素出队,扫描元素插入大顶堆,将更小的元素换到堆中,反复根据上述步骤操作,直到比较完最后一个元素,此时堆里面的就是最小的k个数。
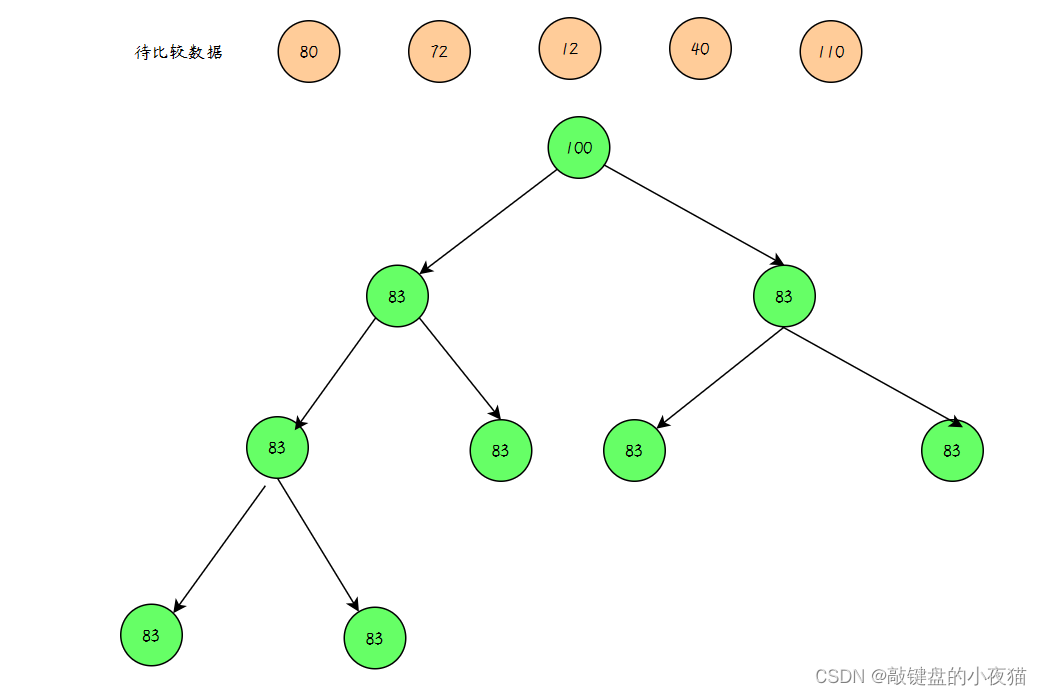
取海量数据里面最大的K个数
要找出数组中最大的k个数,就要【构造一个有k个元素的小顶堆】,小顶堆的堆顶元素值最小,比较堆顶的元素和扫描的元素,如果堆顶元。
素 > 扫描元素,继续扫描其他元素。如果堆顶元素 < 扫描元素 ,将堆顶元素出队,扫描元素插入小顶堆,将更大的元素换到堆中,反复根据上述步骤操作,直到比较完最后一个元素,此时堆里面的就是最大的k个数。
实际应用及实现
问题
如何100亿个数中找出最小的前k个数
问题分析
100亿个数,一个数占四个字节,那么100亿个数就需要40G的存储空间:1G = 10亿字节, 100亿个int = 400亿字节 = 40G。使用普通的电脑和服务器肯定不可能把全部数据,不能创建一个具有100亿个数据的堆,而且使用常规加载进去,存储空间不够大,时间复杂度也是很大。
解决方案
要找出数组中最小的k个数,就要【构造一个有k个元素的大顶堆】,大顶堆的堆顶元素值最大,比较堆顶的元素和扫描的元素,如果堆顶元素 < 扫描元素,继续扫描其他元素。如果堆顶元素 > 扫描元素 ,将堆顶元素出队,扫描元素插入大顶堆,将更小的元素换到堆中,反复根据上述步骤操作,直到比较完最后一个元素,此时堆里面的就是最小的k个数。
代码实现
public class MinTopKHeapSort {/*** 从小到大进行堆排序* @param source*/public static void sort(int[] source,int temp) {//步骤一:构建堆,数组下标0不存储数据int[] heap = new int[source.length + 1];//根据待排序数组,构造一个无序的堆System.arraycopy(source, 0, heap, 1, source.length);//对堆中的元素做下沉调整,从长度的一半处开始,往堆顶索引1处扫描)//二叉堆特性:数组索引一半后的都是叶子节点,不需要做下沉,一半前都是非叶子节点,才需要做for (int i = (heap.length) / 2; i > 0; i--) {down(heap, i, heap.length - 1);}System.out.println("大顶堆:"+Arrays.toString(heap)+", 新元素="+temp);// 循环将数组中剩余的数放入heap数组中,并进行堆排序,如果当前数小于Heap数组中的第一个数,则将当前数替换为第一个数if (temp < heap[1]) {heap[1] = temp;//重新堆化down(heap, 1, source.length-1);}System.arraycopy(heap, 1, source, 0, source.length);}/*** 比较大小,item[left] 元素是否小于 item[right]的元素*/private static boolean rightBig(int[] heap, int left, int right) {return heap[left] < heap[right];}/*** 交互堆中两个元素的位置*/private static void swap(int[] heap, int i, int j) {int temp = heap[i];heap[i] = heap[j];heap[j] = temp;}/*** 使用下沉操作,堆顶和最后一个元素交换后,重新堆化* 不断比较 节点 arr[k]和对应 左节点arr[2*k] 和 右节点arr[2*k+1]的大小,如果当前结点小,则需要交换位置* 直到找到 最后一个索引节点比较完成 则结束*/private static void down(int[] heap, int k, int range) {//当前节点存在左子树while (2 * i < length) {//此时j为左子树节点int j = 2 * i;//如果当前节点存在右子树,并且右子树的值大于左子树的值if (j < length && arr[j + 1] > arr[j]) {//此时j为右子树节点j = j + 1;}//比较当前节点值与其左右子树值的大小if (arr[i] > arr[j]) {break;} else {swap(arr, i, j);i = j;}}}public static void main(String[] args) {//随机数据int[] arr = {923,982,23,1000,1990,12,4,9932,11,34,49,123,1,222,880};// 定义一个长度为k的数组int top = 3;int[] heap = new int[top];// 循环将数组中的前k个数放入Heap数组中; for (int i = 0; i < top; i++) {heap[i] = arr[i];}//循环将数组中剩余的数放入heap数组中,并进行堆排序for(int i = top; i < arr.length; i++){MinTopKHeapSort.sort(heap,arr[i]);}//输出排序后数组中的元素System.out.println("最小的 top k 数据:"+Arrays.toString(heap));}}延申方案
如果是百亿数据,只需要从文本中读取前k个出来,然后构建大顶堆,然后在从剩余的元素逐个读取比较即可
相关文章:
算法之美:堆排序原理剖析及应用案例分解实现
这段时间持续更新关于“二叉树”的专栏文章,关心的小伙伴们对于二叉树的基本原理已经有了初步的了解。接下来,我将会更深入地探究二叉树的原理,并且展示如何将这些原理应用到更广泛的场景中去。文章将延续前面文章的风格,尽量精炼…...
Net8 ABP VNext完美集成FreeSql、SqlSugar,实现聚合根增删改查,完全去掉EFCore
没有基础的,请参考上一篇 彩蛋到最后一张图里找 参考链接 结果直接上图,没有任何业务代码 启动后,已经有了基本的CRUD功能,还扩展了批量删除,与动态查询 动态查询截图,支持分页,排序 实现原理…...
yolov8直接调用zed相机实现三维测距(python)
yolov8直接调用zed相机实现三维测距(python) 1. 相关配置2. 版本一2.1 相关代码2.2 实验结果 3. 版本二3.1 相关代码3.2 实验结果 相关链接 此项目直接调用zed相机实现三维测距,无需标定,相关内容如下: 1.yolov5直接调…...

element跑马灯/轮播图,第一页隐藏左边按钮,最后一页隐藏右边按钮(vue 开箱即用)
图示: 第一步: <el-carousel :class"changeIndex0?leftBtnNone:changeIndeximgDataList.length-1? rightBtnNone:" height"546px" :autoplay"false" change"changeNext"><el-carousel-item v-for…...

下载及安装PHP,composer,phpstudy,thinkPHP6.0框架
文章目录 目录 文章目录 前言 一、下载PHP 二、下载composer 三、下载PHPstudy 四、下载think PHP 1.下载 2.多应用开发 前言 thinkPHP是一款开源的PHP框架,它是基于MVC(Model-View-Controller)设计模式构建的。thinkPHP提供了丰富的…...

volatile使用场景总结
volatile关键字在Java中用于确保变量的可见性以及防止指令重排序,特别是在没有使用锁定机制时对变量进行读写的多线程环境中。以下是需要使用volatile修饰的一些场景: 确保变量的可见性 当一个变量被多个线程访问,且至少有一个线程在写&…...

AcWing 1413. 矩形牛棚(每日一题)
原题链接:1413. 矩形牛棚 - AcWing题库 作为一个资本家,农夫约翰希望通过购买更多的奶牛来扩大他的牛奶业务。 因此,他需要找地方建立一个新的牛棚。 约翰购买了一大块土地,这个土地可以看作是一个 R 行(编号 1∼R&…...
macOS Sonoma 14.4.1 (23E224) 正式版发布,ISO、IPSW、PKG 下载
macOS Sonoma 14.4.1 (23E224) 正式版发布,ISO、IPSW、PKG 下载 2024 年 3 月 26 日凌晨,macOS Sonoma 14.4.1 更新修复了一个可能导致连接到外部显示器的 USB 集线器无法被识别的问题。它还解决了可能导致 Java 应用程序意外退出的问题,并修…...
WPF使用外部字体,思源黑体,为例子
1.在工程中新建文件夹,命名为“Font"。 2.将下载好的字体文件复制到Font文件夹。 3.在工程中,加入静态资源 <Window.Resources><FontFamily x:Key"SYBold">/AnalyzeImage;Component/Font/#思源黑体 CN Bold</FontFamily…...
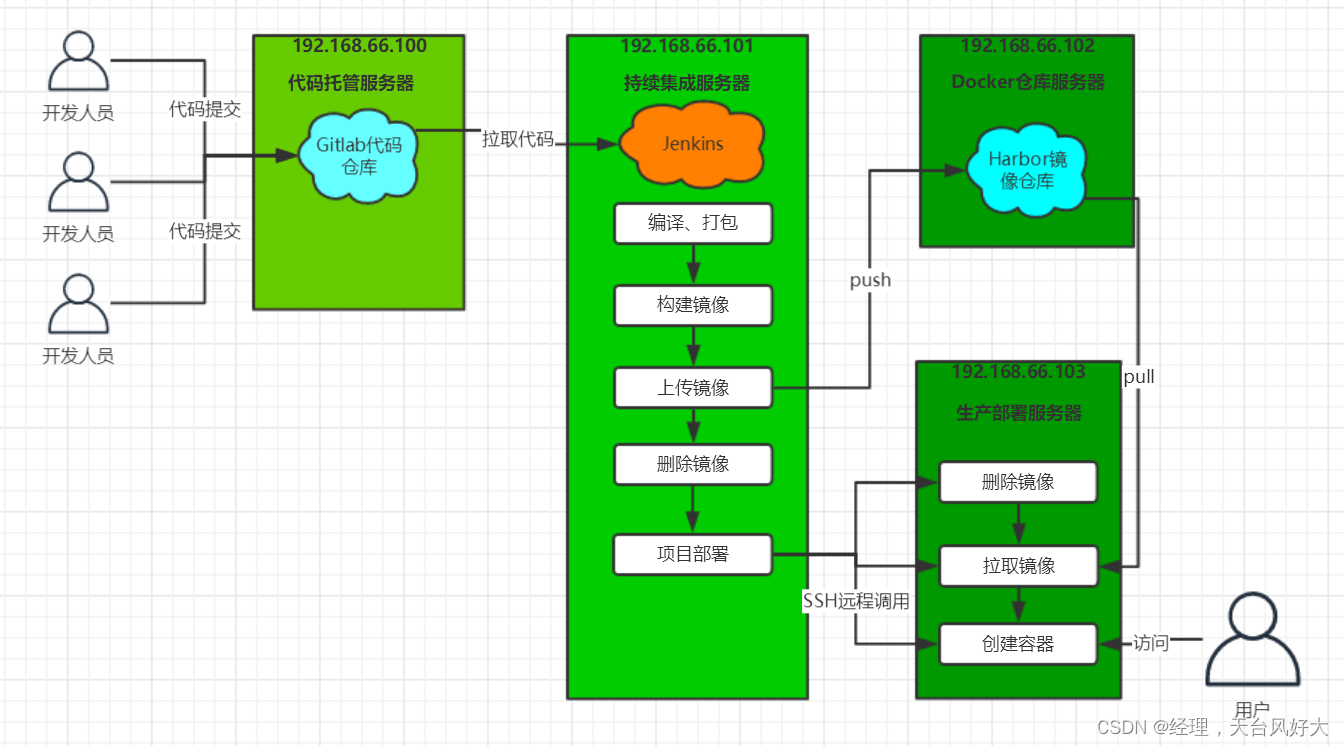
9、jenkins微服务持续集成(一)
文章目录 一、流程说明二、源码概述三、本地部署3.1 SpringCloud微服务部署本地运行微服务本地部署微服务3.2 静态Web前端部署四、Docker快速入门一、流程说明 Jenkins+Docker+SpringCloud持续集成流程说明 大致流程说明: 开发人员每天把代码提交到Gitlab代码仓库Jenkins从G…...

VOC(客户之声)赋能智能家居:打造个性化、交互式的未来生活体验
随着科技的飞速发展,智能家居已成为现代家庭不可或缺的一部分。然而,如何让智能家居更好地满足用户需求,提供更贴心、更智能的服务,一直是行业关注的焦点。在这个背景下,VOC(客户之声)作为一种用…...

时序预测 | Matlab实现GWO-BP灰狼算法优化BP神经网络时间序列预测
时序预测 | Matlab实现GWO-BP灰狼算法优化BP神经网络时间序列预测 目录 时序预测 | Matlab实现GWO-BP灰狼算法优化BP神经网络时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 1.Matlab实现GWO-BP灰狼算法优化BP神经网络时间序列预测(完整源码和数据…...

node.js学习(2)
版权声明 以下文章为尚硅谷PDF资料,B站视频链接:【尚硅谷Node.js零基础视频教程,nodejs新手到高手】仅供个人学习交流使用。如涉及侵权问题,请立即与本人联系,本人将积极配合删除相关内容。感谢理解和支持,…...

【pytest】测试数据存储在 Excel 或 TXT 文件中,如何参数化
如果测试数据存储在 Excel 或 TXT 文件中,你可以使用外部库来读取这些数据,并将其转化为参数化测试所需的格式。下面我将分别展示如何从这两种文件中读取数据,并用于参数化测试。 从 Excel 文件中读取测试数据 你可以使用 pandas 库来读取 …...
ubuntu22.04@Jetson Orin Nano安装配置VNC服务端
ubuntu22.04Jetson Orin Nano安装&配置VNC服务端 1. 源由2. 环境3. VNC安装Step 1: update and install xserver-xorg-video-dummyStep 2: Create config for dummy virtual displayStep3: Add the following contents in xorg.conf.dummyStep 4: Update /etc/X11/xorg.con…...

面向对象特征二:继承
继承的概述 生活中的继承 财产继承: 绿化:前人栽树,后人乘凉 “绿水青山,就是金山银山” 样貌: 继承之外,是不是还可以"进化": 继承有延续(下一代延续上一代的基因、财…...

宝塔面板CentOS Stream 8 x86 下如何安装openlitespeed
宝塔自带的软件商店里如果没办法安装,那么我们可以通过指令来手动安装: 第一步: yum install epel-release Package epel-release-8-19.el8.noarch is already installed. Dependencies resolved. Nothing to do. Complete! 第二步&#…...
)
LeetCode 2952.需要添加的硬币的最小数量:贪心(排序)
【LetMeFly】2952.需要添加的硬币的最小数量:贪心(排序) 力扣题目链接:https://leetcode.cn/problems/minimum-number-of-coins-to-be-added/ 给你一个下标从 0 开始的整数数组 coins,表示可用的硬币的面值ÿ…...
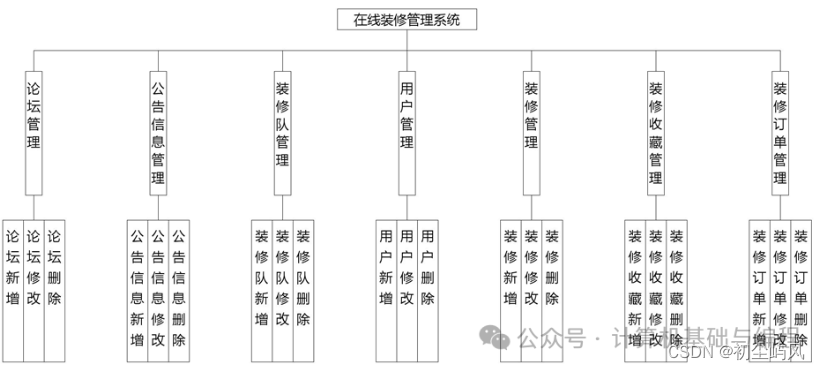
基于SpringBoot + Vue实现的在线装修管理系统设计与实现+毕业论文
介绍 系统包含用户、装修队、管理员三个角色 管理员: 管理员管理:管理其他管理员的账号和权限,确保系统管理的层次化和安全性。 装修队管理:审核装修队的资质,管理装修队的人员信息,监控工程进度ÿ…...
阿里云安全产品简介,Web应用防火墙与云防火墙产品各自作用介绍
在阿里云的安全类云产品中,Web应用防火墙与云防火墙是用户比较关注的安全类云产品,二则在作用上并不是完全一样的,Web应用防火墙是一款网站Web应用安全的防护产品,云防火墙是一款公共云环境下的SaaS化防火墙,本文为大家…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
