【力扣】191.位 1 的个数、485.最大连续 1 的个数
191.位 1 的个数
题目描述
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中 设置位 的个数(也被称为汉明重量)。
示例 1:
输入:n = 11
输出:3
解释:输入的二进制串 1011 中,共有 3 个设置位。
示例 2:
输入:n = 128
输出:1
解释:输入的二进制串 10000000 中,共有 1 个设置位。
示例 3:
输入:n = 2147483645
输出:30
解释:输入的二进制串 11111111111111111111111111111101 中,共有 30 个设置位。
提示:
- 1 <= n <= 231 - 1
进阶:
- 如果多次调用这个函数,你将如何优化你的算法?
解题方法
- C 循环检查
int hammingWeight(int n) {int cnt = 0;unsigned int m = 0x1; // 必须定义为“无符号”型for (int i = 0; i < 32; i++) {if (n & (m << i)) {cnt++;}}return cnt;
}
复杂度分析:
时间复杂度为 O(k),其中 k 是 int 型的二进制位数,k = 32。
空间复杂度为 O(1)。
485. 最大连续 1 的个数
题目描述
给定一个二进制数组 nums , 计算其中最大连续 1 的个数。
示例 1:
输入:nums = [1,1,0,1,1,1]
输出:3
解释:开头的两位和最后的三位都是连续 1 ,所以最大连续 1 的个数是 3.
示例 2:
输入:nums = [1,0,1,1,0,1]
输出:2
提示:
- 1 <= nums.length <= 105
- nums[i] 不是 0 就是 1.
解题方法
- C 遍历取最大
// #define MAX(a, b) ((a) > (b) ? (a) : (b)) // 取最大值int my_max(int a, int b) {if (a > b)return a;elsereturn b;
}int findMaxConsecutiveOnes(int* nums, int numsSize) {int max_cnt = 0, cnt = 0; // 定义最大计数变量,计数变量for (int i = 0; i < numsSize; i++) {if (nums[i] == 1) {cnt++; // 对 1 计数} else {max_cnt = my_max(max_cnt, cnt); // 存储最大 1 的个数cnt = 0; // 重新计数}}max_cnt = my_max(max_cnt, cnt);return max_cnt;
}
复杂度分析
时间复杂度为 O(n),其中 n 是数组的长度。
空间复杂度为 O(1)。
相关文章:

【力扣】191.位 1 的个数、485.最大连续 1 的个数
191.位 1 的个数 题目描述 编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中 设置位 的个数(也被称为汉明重量)。 示例 1: 输入:n 11 输出࿱…...

蓝桥杯 java 承压计算
题目: 思路: 1:其中的数字代表金属块的重量(计量单位较大) 说明每个数字后面不一定有多少个0 2:假设每块原料的重量都十分精确地平均落在下方的两个金属块上,最后,所有的金属块的重量都严格精确地平分落在最底层的电子…...

leetcode268-Missing Number
这道题目要求缺失的数字,一般解决数组的问题,要么往排序数组,要么往双指针遍历这些方向上靠,要么往异或方向上靠,总之落点无非就只有这几个。我们要求缺失的数字,可以依次让1~n和数组元素进行异…...
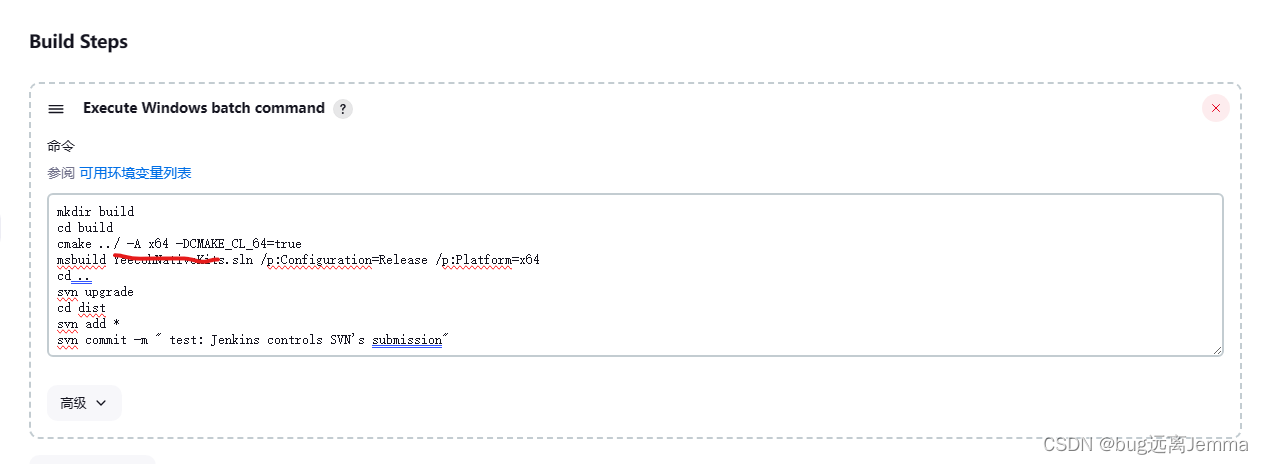
【jenkins+cmake+svn管理c++项目】jenkins回传文件到svn(windows)
书接上文:创建一个项目 在经过cmakemsbuild顺利生成动态库之后,考虑到我一个项目可能会生成多个动态库,它们分散在build内的不同文件夹,我希望能将它们收拢到一个文件夹下,并将其回传到svn。 一、动态库移位—cmake实…...
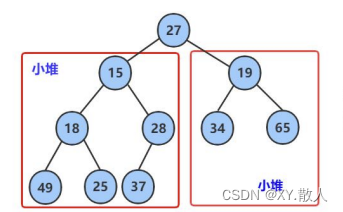
数据结构·二叉树(2)
目录 1 堆的概念 2 堆的实现 2.1 堆的初始化和销毁 2.2 获取堆顶数据和堆的判空 2.3 堆的向上调整算法 2.4 堆的向下调整算法 2.4 堆的插入 2.5 删除堆顶数据 2.6 建堆 3 建堆的时间复杂度 3.1 向上建堆的时间复杂度 3.2向下建堆的时间复杂度 4 堆的排序 前言&…...

MATLAB算法实战应用案例精讲-【毕业季论文专用】人工智能视觉检测技术及其在实际应用中的挑战与前景
目录 摘要: 第一章:引言 1.1 研究背景 1.2 研究目的与意义...
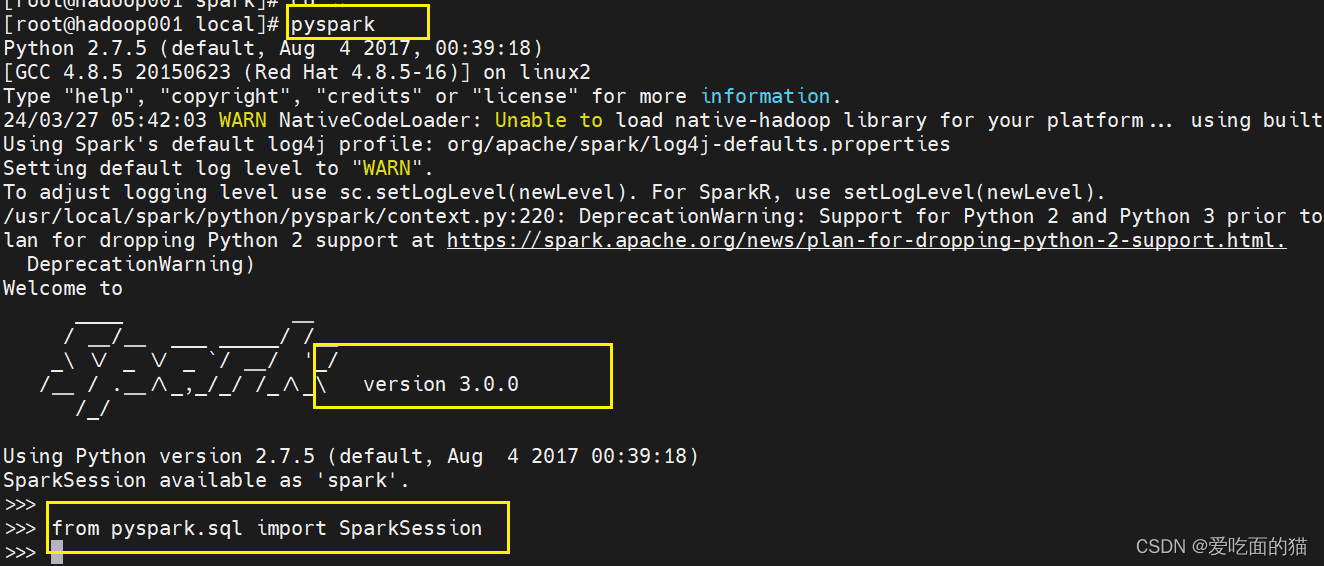
Linux虚拟机环境搭建spark
Linux环境搭建Spark分为两个版本,分别是Scala版本和Python版本。 一、 安装Pyspark 本环境以 Python 环境为例。 1、下载spark 下载网址:https://archive.apache.org/dist/spark 下载安装包:根据自己环境选择合适版本,本环境…...

STL的string容器
string基本概念 string是C风格的字符串,本质上是一个类。 string 和 char* 的区别 char* 是一个指针; string是一个类,内部封装了 char* ,用来管理字符串,是一个 char* 型的容器。 特点 string内部封装了很多成员…...

半导体工艺技术
完整内容点击:【半导体工艺技术】...

acwing算法提高之图论--单源最短路的扩展应用
目录 1 介绍2 训练 1 介绍 本专题用来记录使用。。。。 2 训练 题目1:1137选择最佳线路 C代码如下, #include <iostream> #include <cstring> #include <algorithm> #include <queue>using namespace std;const int N 101…...

SQLServer数据库使用Function实现根据字段内容的拼音首字母进行数据查询
实现SQL首字母查询分两步,第一步建Function,第二步引用新建的Function。 1. 首先需要自定义一个查询的Function,详细SQL如下: ALTER function [dbo].[GetDataByPY](str nvarchar(4000)) returns nvarchar(4000) as begin decla…...
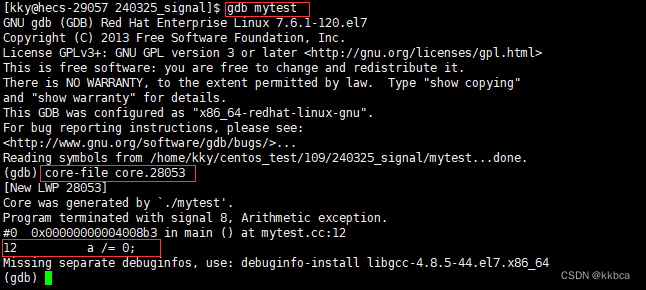
Linux——信号概念与信号产生方式
目录 一、概念 二、前台进程与后台进程 1.ctrlc 2.ctrlz 三、信号的产生方式 1.键盘输入产生信号 2.系统调用发送信号 2.1 kill()函数 2.2 raise()函数 2.3 abort()函数 3.异常导致信号产生 3.1 除0异常 3.2 段错误异常 4.软件条件产生信号 4.1 管道 4.2 闹钟…...
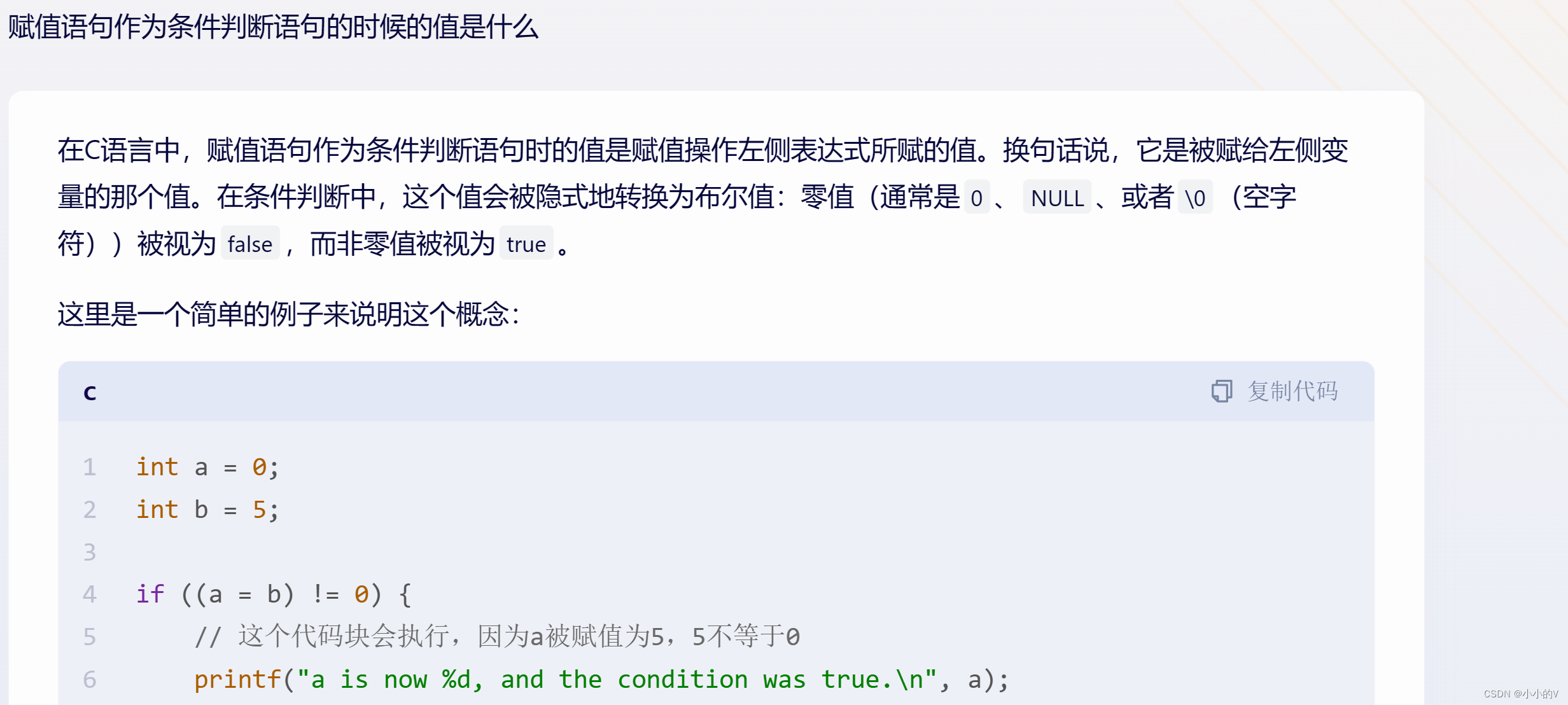
赋值语句还能当判断条件?涨芝士了!
赋值和条件看似是C语言中毫不相关的两个概念,虽然实际过程中我猜测不会有太多这种不太符合常理的情况出现,但是现在在学习的过程中,为了出题而出题总是会整出一些花活出来.....这很难不让人联想起高中时一些大佬为了彰显自己的数学天赋而自己…...
数据结构 - 算法效率|时间复杂度|空间复杂度
目录 1.算法效率 2.时间复杂度 2.1定义 2.2大O渐近表示法 2.3常见时间复杂度计算举例 3.空间复杂度 3.1定义 3.2常见空间复杂度计算举例 1.算法效率 算法的效率常用算法复杂度来衡量,算法复杂度描述了算法在输入数据规模变化时,其运行时间和空间…...
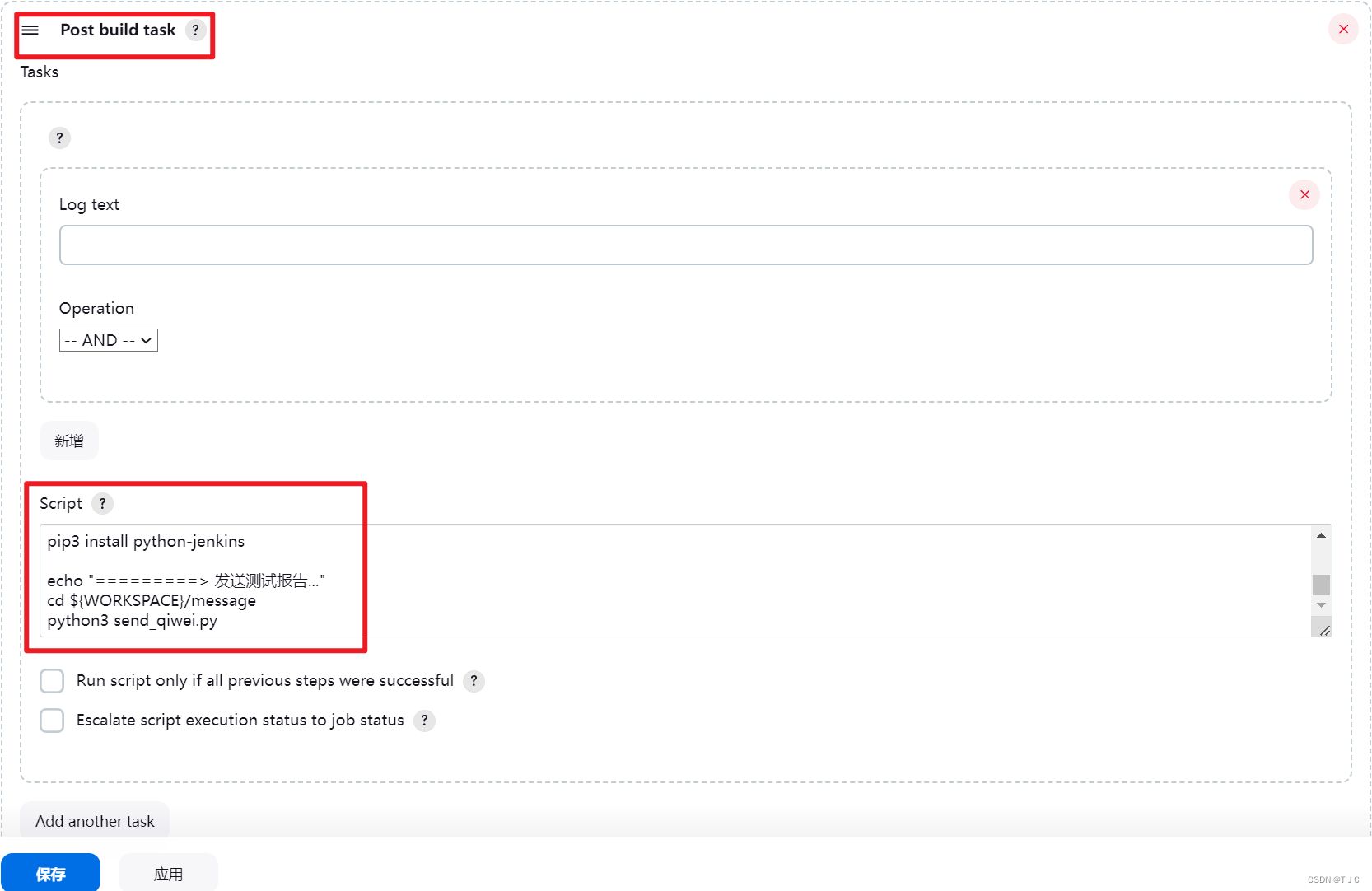
接口自动化之 + Jenkins + Allure报告生成 + 企微消息通知推送
接口自动化之 Jenkins Allure报告生成 企微消息通知推送 在jenkins上部署好项目,构建成功后,希望可以把生成的报告,以及结果统计发送至企微。 效果图: 实现如下。 1、生成allure报告 a. 首先在Jenkins插件管理中&#x…...

『Apisix安全篇』探索Apache APISIX身份认证插件:从基础到实战
🚀『Apisix系列文章』探索新一代微服务体系下的API管理新范式与最佳实践 【点击此跳转】 📣读完这篇文章里你能收获到 🛠️ 了解APISIX身份认证的重要性和基本概念,以及如何在微服务架构中实施API安全。🔑 学习如何使…...
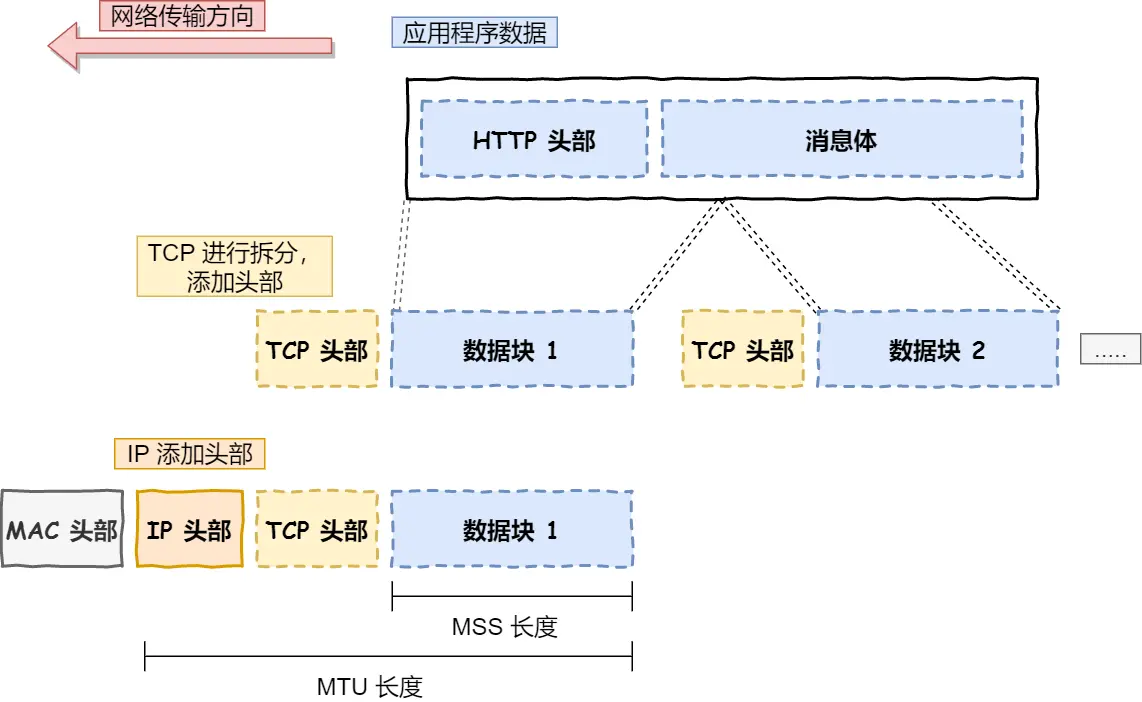
【01-20】计算机网络基础知识(非常详细)从零基础入门到精通,看完这一篇就够了
【01-20】计算机网络基础知识(非常详细)从零基础入门到精通,看完这一篇就够了 以下是本文参考的资料 欢迎大家查收原版 本版本仅作个人笔记使用1、OSI 的七层模型分别是?各自的功能是什么?2、说一下一次完整的HTTP请求…...
)
『大模型笔记』常见的分布式并行策略(分布式训练)
常见的分布式并行策略(分布式训练) 文章目录 一. 为什么分布式训练越来越流行二. 常见的并行策略2.1 数据并行2.2 模型并行2.3 流水并行2.4 混合并行二. 参考文献一. 为什么分布式训练越来越流行 近年来,深度学习被广泛应用到各个领域,包括计算机视觉、语言理解、语音识别、广…...
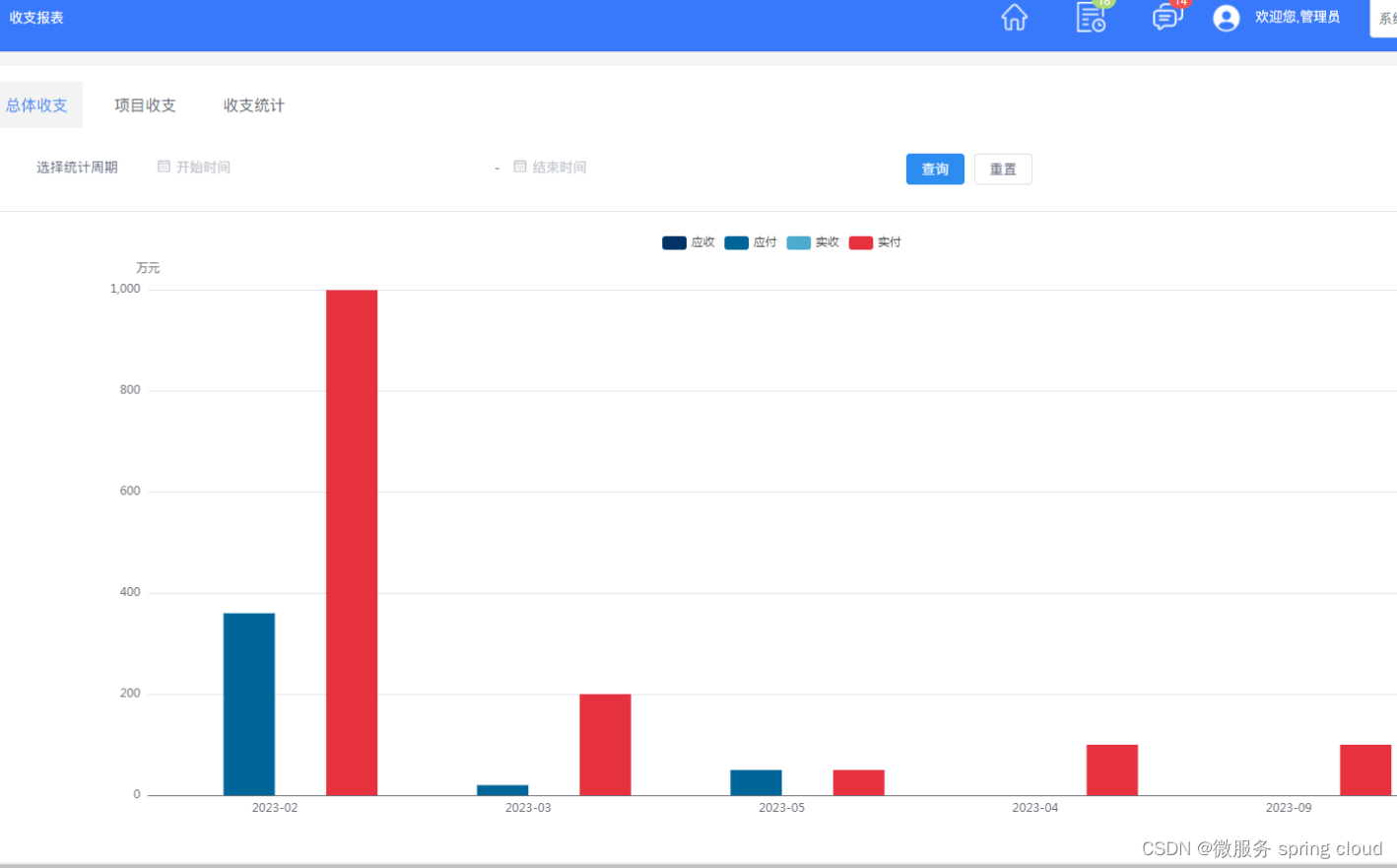
java 企业工程管理系统软件源码+Spring Cloud + Spring Boot +二次开发+ 可定制化
工程项目管理软件是现代项目管理中不可或缺的工具,它能够帮助项目团队更高效地组织和协调工作。本文将介绍一款功能强大的工程项目管理软件,该软件采用先进的Vue、Uniapp、Layui等技术框架,涵盖了项目策划决策、规划设计、施工建设到竣工交付…...
3D数据格式导出工具HOOPS Publish如何生成高质量3D PDF?
在当今数字化时代,从建筑设计到制造业,从医学领域到电子游戏开发,3D技术已经成为了不可或缺的一部分。在这个进程中,将3D模型导出为3D PDF格式具有重要的意义。同时,HOOPS Publish作为一个领先的解决方案,为…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...

基于 HTTP 的单向流式通信协议SSE详解
SSE(Server-Sent Events)详解 🧠 什么是 SSE? SSE(Server-Sent Events) 是 HTML5 标准中定义的一种通信机制,它允许服务器主动将事件推送给客户端(浏览器)。与传统的 H…...
