【stable diffusion扩散模型】一篇文章讲透
目录
一、引言
二、Stable Diffusion的基本原理
1 扩散模型
2 Stable Diffusion模型架构
3 训练过程与算法细节
三、Stable Diffusion的应用领域
1 图像生成与艺术创作
2 图像补全与修复
3 其他领域
四、Stable Diffusion的优势与挑战
👉优势
👉挑战
五、Stable Diffusion的未来发展
1 技术进步的影响
2 应用拓展
3 挑战与解决方案
六、结论
一、引言
随着科技的飞速发展,图像生成技术逐渐成为了人工智能领域的一个研究热点。从早期的简单图像处理到如今的深度学习生成模型,图像生成技术不断突破,为人们带来了前所未有的视觉体验。在这个背景下,Stable Diffusion作为一种新型的图像生成技术,以其独特的优势引起了广泛关注。本文将介绍Stable Diffusion的基本原理、应用领域、优势与挑战,并展望其未来发展。
二、Stable Diffusion的基本原理
👇推荐这篇文章https://arxiv.org/pdf/1706.03762.pdf
1 扩散模型
Stable Diffusion是一种基于扩散模型的图像生成技术。扩散模型是一种概率模型,通过模拟数据分布的扩散过程来生成新的数据。在Stable Diffusion中,模型首先学习大量图像数据的统计规律,然后利用这些规律来生成新的图像。
2 Stable Diffusion模型架构
Stable Diffusion的模型架构通常包括编码器、扩散过程和解码器三个部分。编码器负责将输入的图像转换为潜在的表示,扩散过程则在潜在的表示上进行随机扰动,最后解码器将扰动后的表示还原为图像。通过这种方式,Stable Diffusion能够生成具有多样性和真实感的图像。
3 训练过程与算法细节
在训练过程中,Stable Diffusion采用了一种特殊的算法来优化模型参数。通过不断迭代和调整参数,模型能够逐渐学习到数据的内在规律,并生成高质量的图像。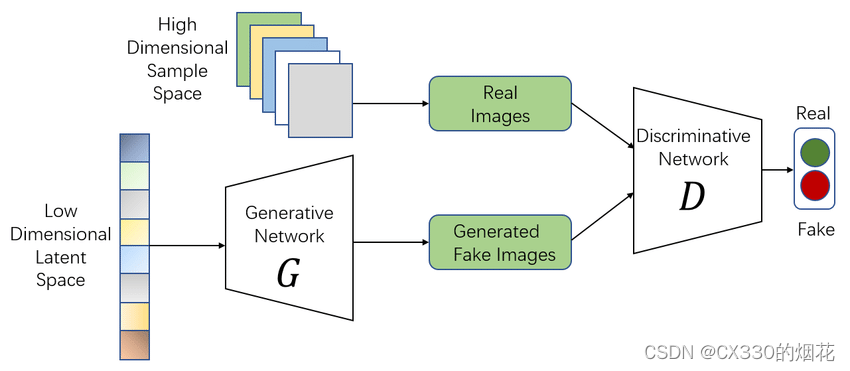
三、Stable Diffusion的应用领域
1 图像生成与艺术创作
首先,在图像生成与艺术创作方面,Stable Diffusion能够生成具有独特风格和创意的图像。通过调整模型的参数和输入条件,艺术家可以创作出丰富多样的艺术作品。此外,Stable Diffusion还可以用于风格迁移,将一种风格的图像转换为另一种风格,为艺术创作提供更多的可能性。
2 图像补全与修复
其次,Stable Diffusion在图像补全与修复方面也具有重要作用。当图像的某部分缺失或损坏时,Stable Diffusion可以根据图像的剩余部分生成缺失或损坏的内容,实现图像的自动补全和修复。这对于图像处理、文物保护等领域具有重要意义。
3 其他领域
此外,Stable Diffusion还可以应用于虚拟现实与增强现实、医学影像处理、游戏设计与开发等领域。在虚拟现实与增强现实中,Stable Diffusion可以生成逼真的虚拟场景和物体,提升用户体验;在医学影像处理中,Stable Diffusion可以帮助医生更好地分析和诊断疾病;在游戏设计与开发中,Stable Diffusion可以生成丰富的游戏场景和角色,提高游戏的趣味性和可玩性。
四、Stable Diffusion的优势与挑战
👉优势
Stable Diffusion作为一种新型的图像生成技术,具有许多优势。
- 首先,它能够生成高质量的图像,具有真实感和多样性。
- 其次,Stable Diffusion具有广泛的应用领域,可以应用于艺术创作、图像处理、虚拟现实等多个领域。
- 此外,随着技术的不断进步,Stable Diffusion的生成速度和效率也在不断提高。
👉挑战
然而,Stable Diffusion也面临着一些挑战。
- 首先,计算资源需求大是Stable Diffusion面临的一个主要问题。由于模型需要处理大量的图像数据,因此需要高性能的计算设备和大量的存储空间。
- 其次,模型的稳定性与收敛性也是一个需要解决的问题。在训练过程中,模型可能会出现不稳定或难以收敛的情况,影响生成图像的质量。
- 此外,伦理与版权问题也是Stable Diffusion需要关注的一个方面。在生成图像时,需要确保不侵犯他人的版权和隐私,并遵守相关的伦理规范。
五、Stable Diffusion的未来发展
1 技术进步的影响
随着技术的不断进步,Stable Diffusion有望在未来取得更大的发展。首先,随着计算能力的提升和算法的优化,Stable Diffusion的生成速度和效率将得到进一步提高。这将使得Stable Diffusion能够更广泛地应用于各个领域,为人们带来更好的体验和服务。
2 应用拓展
其次,Stable Diffusion在应用领域上也将不断拓展。除了现有的艺术创作、图像处理等领域外,Stable Diffusion还有望在医学影像处理、自动驾驶、智能制造等领域发挥更大的作用。通过与其他技术的结合,Stable Diffusion将为这些领域提供更高效、更准确的解决方案。
3 挑战与解决方案
然而,面对挑战和问题,我们也需要寻找相应的解决方案。例如,通过优化算法和模型结构来降低计算资源需求;通过引入正则化等技术来提高模型的稳定性与收敛性;通过加强版权保护意识和伦理规范来确保技术的健康发展。
六、结论
Stable Diffusion作为一种新型的图像生成技术,以其独特的优势在多个领域展现出了广泛的应用前景。通过不断优化算法和模型结构,解决面临的挑战和问题,Stable Diffusion有望在未来取得更大的发展,为人们带来更好的视觉体验和服务。我期待着Stable Diffusion在图像生成领域的更多创新和突破,为人工智能技术的发展贡献更多的力量。
相关文章:

【stable diffusion扩散模型】一篇文章讲透
目录 一、引言 二、Stable Diffusion的基本原理 1 扩散模型 2 Stable Diffusion模型架构 3 训练过程与算法细节 三、Stable Diffusion的应用领域 1 图像生成与艺术创作 2 图像补全与修复 3 其他领域 四、Stable Diffusion的优势与挑战 👉优势 …...

数据链路层之信道:数字通信的桥梁与守护者
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua小谢,在这里我会分享我的知识和经验。&am…...

SQL109 纠错4(组合查询,order by..)
SELECT cust_name, cust_contact, cust_email FROM Customers WHERE cust_state MI UNION SELECT cust_name, cust_contact, cust_email FROM Customers WHERE cust_state IL ORDER BY cust_name;order by子句,必须位于最后一条select语句之后...

Spring Boot + Vue 实现文件导入导出功能
文章目录 1、概述2、后端实现(Spring Boot)3、前端实现(Vue)4、总结 1、概述 在现代Web应用开发中,文件的导入导出是一个常见的需求。Spring Boot作为后端开发的强大框架,搭配前端框架Vue,可…...
vue watch 深度监听
vue2文档:API — Vue.js vue3文档:侦听器 | Vue.js watch 可以用来监听页面中的数据,但如果监听的源是对象或数组,则使用深度监听,强制深度遍历源,以便在深度变更时触发回调。 一,监听 <t…...
Qt源码调试步骤记录
1.源码: 两种方式,要么安装qt时选择source,要么从官网下载源码,然后在qt creator中设置路径。二选一即可。我选的第二种。 1.1.第一种,安装时选择source: 1.2.第二种,下载源码设置路径&#x…...
)
大数据面试英文自我介绍参考(万字长文)
发现有一个怪圈,如果码农年龄35+,除非非常匹配,不然在国内企业筛选可能就筛选不过。国外码农可以干到40+、50+。一些外企,对年龄35+的码农依然青睐。这些外企对英文是有要求,通常是要英文自我介绍,下面提供一些英文自我介绍参考。 参考1: Good morning/afternoon, I a…...

外包干了5天,技术退步明显.......
先说一下自己的情况,大专生,18年通过校招进入杭州某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落! 而我已经在一个企业干了四年的功能测…...
Docket常见的软件部署1
1 安装MySQL # 查看MySQL镜像 docker search mysql # 拉起镜像 docker pull mysql:5.7 # 创建MySQL数据映射卷,防止数据不丢失 mkdir -p /hmoe/tem/docker/mysql/data/ # 启动镜像 docker run -d --name mysql -e MYSQL_ROOT_PASSWORD123456 -p 3306:3306 -v /home…...
Qt源程序编译及错误问题解决
Error 5 while parsing C:/qt-everywhere-src-6.6.2/qt-build/qtdeclarative/src/qmlmodels/meta_types/qt6qmlmodels_release_metatypes.json: illegal value .json 文件为空文件0字节,加 “[]”,不要引号。可以解决这类错误。 Qt编译 Qt for Windows…...
)
作业练习(python)
第一题: cel eval(input()) fah 9 / 5 * cel 32 print("%.1f" % fah) 第二题: radius, length eval(input()) area radius * radius * 3.14159267 volume area * length print("%.2f" % area) print("%.2f" …...
Wireshark使用相关
1.wireshark如何查看RST包 tcp.flags.reset1 RST表示复位,用来异常的关闭连接,在TCP的设计中它是不可或缺的。发送RST包关闭连接时,不必等缓冲区的包都发出去(不像上面的FIN包),直接就丢弃缓存区的包发送R…...

相机标定学习记录
相机标定是计算机视觉和机器视觉领域中的一项基本技术,它的主要目的是通过获取相机的内部参数(内参)和外部参数(外参),以及镜头畸变参数,建立起现实世界中的点与相机成像平面上对应像素点之间准…...

CSS 滚动条样式修改
1、滚动条整体部分 使用 ::-webkit-scrollbar 注意:这个必须要加,不然修改的样式不生效 ::-webkit-scrollbar {width: 10px;//修改滚动条宽度 }2、滚动条中的滑块 使用 ::-webkit-scrollbar-thumb ::-webkit-scrollbar-thumb {border-radius: 8px;b…...
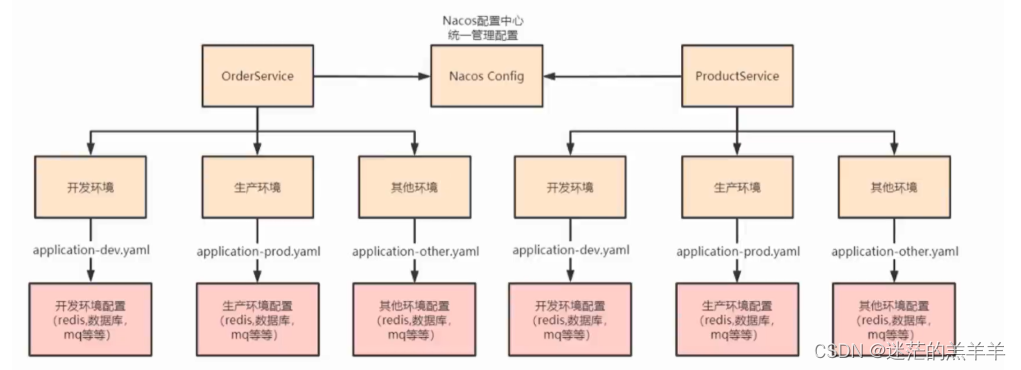
谈谈配置中心?
配置中心可以做集中式的服务配置管理,比如配置一些数据库连接的URL,一些共用的配置且可动态调整的参数。如果不采用集中式的管理,会导致修改起来特别麻烦,一个个的修改特别繁琐。 Nacos Config配置中心中采用的是客户端拉取数据&a…...
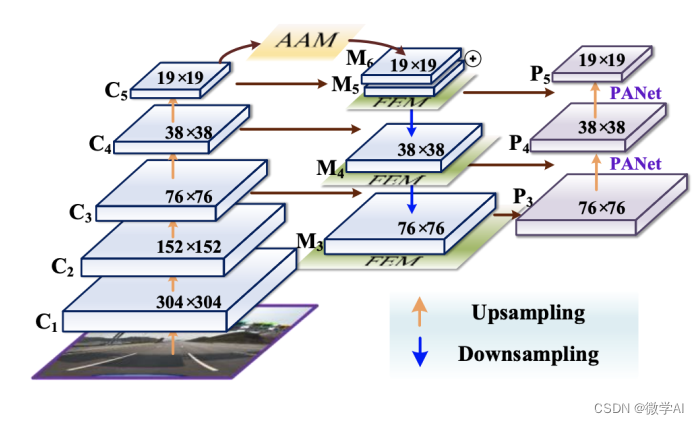
人工智能(pytorch)搭建模型25-基于pytorch搭建FPN特征金字塔网络的应用场景,模型结构介绍
大家好,我是微学AI,今天给大家介绍一下人工智能(pytorch)搭建模型25-基于pytorch搭建FPN特征金字塔网络的应用场景,模型结构介绍。特征金字塔网络(FPN)是一种深度学习模型结构,主要应用于目标检测任务中&am…...
JRT业务开发起步
这是一段充满挑战与奋斗的旅程,自第一行Java代码的写下起,便历经重重险阻。从细微的代码行,逐步汇聚成实用的工具类方法;从工具类方法的积累,逐渐构建起功能强大的工具包;再从工具包的整合,最终…...

深度解析:国内主流音视频产品的核心功能与市场表现
前言 当前音视频开发领域呈现出多样化竞争态势,其中声网(Agora)、即构(ZEGO)等云通讯企业占据了市场的主导地位。随着技术的持续进步和用户需求的日益多样化,选择音视频服务提供商的标准也越来越个性化&am…...
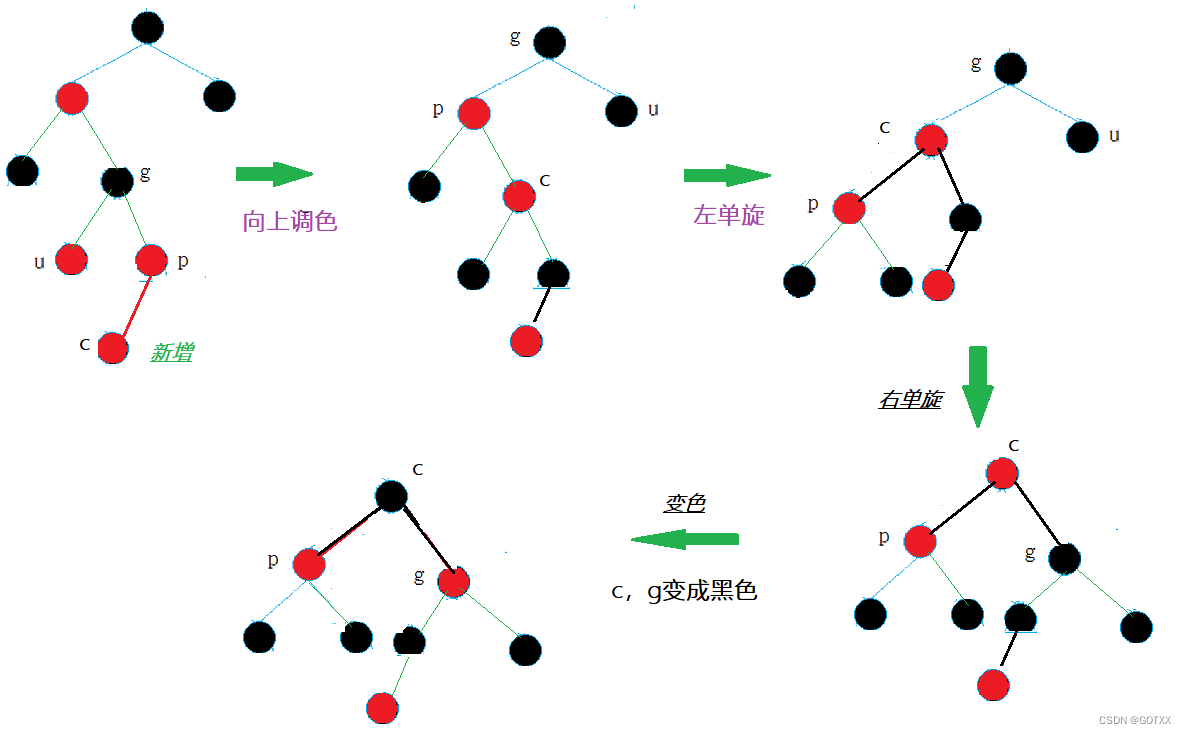
红黑树介绍及插入操作的实现
🎉个人名片: 🐼作者简介:一名乐于分享在学习道路上收获的大二在校生 🙈个人主页🎉:GOTXX 🐼个人WeChat:ILXOXVJE 🐼本文由GOTXX原创,首发CSDN&…...

[linux初阶][vim-gcc-gdb] TwoCharter: gcc编译器
目录 一.Linux中gcc编译器的下载与安装 二.使用gcc编译器来翻译 C语言程序 ①.编写C语言代码 ②翻译C语言代码 a.预处理 b.编译 c.汇编 d.链接 ③.执行Main 二进制可执行程序(.exe文件) 三.总结 一.Linux中gcc编译器的下载与安装 使用yum命令(相当于手机上的应用…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
