LeetCode_二分搜索_困难_154.寻找旋转排序数组中的最小值 II
目录
- 1.题目
- 2.思路
- 3.代码实现(Java)
1.题目
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到:
- 若旋转 4 次,则可以得到 [4,5,6,7,0,1,4]
- 若旋转 7 次,则可以得到 [0,1,4,4,5,6,7]
注意,数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。给你一个可能存在重复元素值的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的最小元素。
你必须尽可能减少整个过程的操作步骤。
示例 1:
输入:nums = [1,3,5]
输出:1
示例 2:
输入:nums = [2,2,2,0,1]
输出:0
提示:
n == nums.length
1 <= n <= 5000
-5000 <= nums[i] <= 5000
nums 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
进阶:这道题与 寻找旋转排序数组中的最小值 类似,但 nums 可能包含重复元素。允许重复会影响算法的时间复杂度吗?会如何影响,为什么?
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array-ii
2.思路
(1)二分搜索
本题与153.寻找旋转排序数组中的最小值这题类似,只不过本题中的 nums 数组可能包含重复元素。
相关题目:
LeetCode_二分搜索_中等_33.搜索旋转排序数组
LeetCode_二分搜索_中等_81.搜索旋转排序数组 II
LeetCode_二分搜索_中等_153.寻找旋转排序数组中的最小值
3.代码实现(Java)
//思路1————二分搜索
class Solution {public int findMin(int[] nums) {int left = 0;int right = nums.length - 1;while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] > nums[right]) {//如果 nums[mid] > nums[right],说明最小值在 mid 右侧left = mid + 1;} else if (nums[mid] < nums[right]) {//如果 nums[mid] < nums[right],说明最小值在 mid 左侧或者就是 mid 本身right = mid;} else {//如果 nums[mid] == nums[right],我们无法判断最小值在 mid 的左侧还是右侧,因此将右边界缩小一位right--;}}return nums[left];}
}
相关文章:

LeetCode_二分搜索_困难_154.寻找旋转排序数组中的最小值 II
目录1.题目2.思路3.代码实现(Java)1.题目 已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,4,4,5,6,7] 在变化后可能得到: 若旋转 4…...

面向对象设计模式:创建型模式之建造者模式
一、引入 Build:建造和构建具有建筑结构的大型物体 建楼:打牢地基、搭建框架、然后自下而上一层层盖起来。构建物体:通常需要先建造组成这个物体的各个部分,然后分阶段把它们组装起来 二、建造者模式 2.1 Intent 意图 Separate…...

集成学习boosting、bagging、stacking
目录 一、介绍 二、三种架构学习 (1)boosting (2)bagging (3)stacking 一、介绍: 对于单个模型来说很难拟合复杂的数,模型的抗干扰能力较低,所以我们希望可以集成多…...

数据模型(上):模型分类和模型组成
1.模型分类 数据模型是一种由符号、文本组成的集合,用以准确表达信息景观,达到有效交流、沟通的目的。数据建模者要求能与来自不同部门,具有不同技术背景,不同业务经验,不同技术水平的人员交流、沟通。数据建模者要了解每个人员的观点,并通过反馈证明理解无误,最终作…...
 数据结构题目集 - ZZULI)
郑州轻工业大学2022-2023(2) 数据结构题目集 - ZZULI
6-1 线性表元素的区间删除 6-1 线性表元素的区间删除 分数 20 全屏浏览题目 切换布局 作者 DS课程组 单位 浙江大学 给定一个顺序存储的线性表,请设计一个函数删除所有值大于min而且小于max的元素。删除后表中剩余元素保持顺序存储,并且相对位置不能改变…...

【Python语言基础】——Python MySQL Drop Table
Python语言基础——Python MySQL Drop Table 文章目录Python语言基础——Python MySQL Drop Table一、Python MySQL Drop Table一、Python MySQL Drop Table 删除表 您可以使用 “DROP TABLE” 语句来删除已有的表: 实例 删除 “customers” 表: import…...

2023美团面试真题
面试前需要准备: 1. Java 八股文:了解常考的题型和回答思路; 2. 算法:刷 100-200 道题,记住刷题最重要的是要理解其思想,不要死记硬背,碰上原题很难,但 大多数的解题思路是相通的…...
【微信小程序开发全流程】篇章0:基于JavaScript开发的校园综合类微信小程序的概览
基于JavaScript开发的校园综合类微信小程序的概览 本文仅供学习,未经同意请勿转载 一些说明:上述项目来源于笔者我本科大三阶段2019年电子设计课程项目,在这个项目中,我主要是负责的部分有前端,前后端的对接…...

如何分析sql性能
1、前言 提到sql性能分析,可能都会想到explain,它在mysql里被称为执行计划,也就是说可以通过该命令看出mysql在通过优化器分析之后如何执行sql。mysql的内置优化器十分强大,它能帮我们把sql再次优化,以最低的成本去执…...

市场营销书籍推荐:《经理人参阅:市场营销》
要学好市场营销有什么好方法?答案是看书!比起碎片化地去阅读一些文章或看一些相关视频,读书来得更实在些。倘若能静下心来好好读上一本系统性的市场营销书籍,学好营销管理将不会再是一件难事。然而,问题的关键是&#…...

WPF 控件专题 MediaElement控件详解
1、MediaElement 介绍 MediaElement:表示包含音频和/或视频的控件。 MediaOpened在引发事件之前,ActualWidth控件将ActualHeight报告为零,因为媒体内容用于确定控件的最终大小和位置。 对于仅音频内容,这些属性始终为零。 对于固…...

基于SpringBoot+SpringCloud+Vue前后端分离项目实战 --开篇
本文目录前言做项目的三大好处强强联手(天狗组合)专栏作者简介专栏的优势后端规划1. SpringBoot 和 SpringCloud 的选择2. Mybatis 和 MybatisPlus 和 JPA 的选择3. MySQL 和 Mongodb 的选择4. Redis 和 RocketMQ5. 后端规划小总结后端大纲提前掌握的知识点一期SpringBoot二期S…...

循环队列的实现
我们知道队列的实现可以用单链表和数组,但是循环链表也可以使用这两种方式。首先我们来看看单链表:首先使用单链表,我们需要考虑循环队列的一些特点。单链表实现循环队列我们要考虑几个核心问题:首先我们要区别 解决 空 和 满 的问…...
MTK平台开发入门到精通(休眠唤醒篇)休眠唤醒LPM框架
文章目录 一、lpm驱动源码分析二、设备属性调试文件沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇文章将介绍 lpm 驱动源码分析。 mtk 平台下,其默认的 lpm 机制的源码位置:drivers/misc/mediatek/lpm/ 一、lpm驱动源码分析 目录:drivers/misc/mediatek/lpm/…...
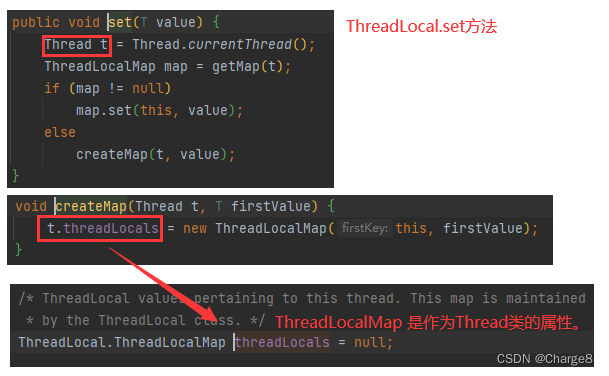
ThreadLocal详解
一、ThreadLocal简介 1、简介 ThreadLocal叫做线程变量,它是一个线程的本地变量,意味着这个变量是线程独有的,是不能与其他线程共享的。这样就可以避免资源竞争带来的多线程的问题。 即 ThreadLocal类用来提供线程内部的局部变量࿰…...
利用Cookie劫持+HTML注入进行钓鱼攻击
目录 HTML注入和cookie劫持: 发现漏洞 实际利用 来源 HTML注入和cookie劫持: HTML注入漏洞一般是由于在用户能够控制的输入点上,由于缺乏安全过滤,导致攻击者能将任意HTML代码注入网页。此类漏洞可能会引起许多后续攻击&#…...

【接口汇总】常用免费的API
短信API 短信验证码:可用于登录、注册、找回密码、支付认证等等应用场景。支持三大运营商,3秒可达,99.99%到达率,支持大容量高并发。 通知短信:当您需要快速通知用户时,通知短信是最快捷有效的…...

数字信号处理知识点
数字信号处理知识点1 频谱图中,横坐标取值范围的含义2 MATLAB常用函数2.1 波形产生2.2 滤波器分析2.3 滤波器实现2.4 线性系统变换2.5 滤波器设计2.5.1 FIR滤波器2.5.2 IIR滤波器2.6 Transforms(变换)2.7 统计信号处理和谱分析2.8 Windows(窗函数)2.9 Parametric Mo…...

计算机网络第八版——第三章课后题答案(超详细)
第三章 该答案为博主在网络上整理,排版不易,希望大家多多点赞支持。后续将会持续更新(可以给博主点个关注~ 第一章 答案 第二章 答案 【3-01】数据链路(即逻辑链路)与链路(即物理链路)有何区…...
九龙证券|磷酸亚铁锂是什么?磷酸亚铁锂的特点和性能介绍
磷酸亚铁锂是一种新式锂离子电池电极资料,化学式:LiFePO4,磷酸亚铁锂为近来新开发的锂离子电池电极资料,首要用于动力锂离子电池,作为正极活性物质运用,人们习气也称其为磷酸铁锂。 磷酸亚铁锂的特色和功能…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
