蓝桥杯22年第十三届省赛-统计子矩阵|一维前缀和加双指针
题目链接:
1.统计子矩阵 - 蓝桥云课 (lanqiao.cn)
蓝桥杯2022年第十三届省赛真题-统计子矩阵 - C语言网 (dotcpp.com)
说明:
涉及到子矩阵的时候,一般就跟前缀和相关,可以降维。
先回顾一下最大子矩阵,回忆一下一维前缀和的模板,枚举列(行也可以,计算前缀和时就算列上的前缀和)的起点和终点,求每行上的元素之和的时候时间优化为O(1):
最大子段和和最大子矩阵|动态规划-CSDN博客
如果列的起点和终点确定,那么求小于k的子矩阵个数其实就是求第1行到第m行有多少个和小于k的连续子序列。
用l,r表示这个子序列的左右端点,
如果
因为矩阵元素都为正数
1.sum(l,r)<k,那么sum(i,r)<k ; l<=i<=r,合法的新子序列个数就是r-l+1;
2.sum(l,r)>k,那么sum(l,j)>k;r<=j<=m, 当前区间已经大于k了,没必要再继续向下挪动r了,那就移动l
再注意一下自己的错误:
//错误代码,不能加这个判断 ,因为,当t和b都指向一个元素时,这个元素还大于k//s减为0,t移动到b+1位置,并且接下来仍有可能出现小于k的矩阵 //if(t>b) break;/*错误代码,因为此时小于k的矩阵不止一个,而是 b-t+1个即i+1列到j列上,t行到b行的矩阵和小于k,那么,固定t, t到b-1行也小于kt到b-2行也小于k,t到X(t<=X<=b)行都小于k,应该加上t到b的数字个数反过来也一样,b移动到下个位置小于k,将b固定,b行到t行 也是 b-t+1个if(s<=k) {ans++;}*/总结一下:
- 子矩阵问题可能会用前缀和降维
- 求小于某个值的连续子序列的数量时,使用双指针。l和r都起始点开始,移动r指针,序列和小于k时,新答案有r-l+1个;大于k时,移动l指针直到小于k。
代码:
只用前缀和的版本,两层循环控制列的起点和终点,两层循环控制行的起点和终点。会超时。
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N =500+10;
int ans = 0;
int k;int mx[N][N]={0};
signed main() {ios::sync_with_stdio(0); cin.tie(0);cout.tie(0);int m,n;cin>>m>>n;cin>>k;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){cin>>mx[i][j];mx[i][j]+=mx[i][j-1];}}for(int i=0;i<=n-1;i++){for(int j=i+1;j<=n;j++){for(int t=1;t<=m;t++){int s=0;for(int b=t;b<=m;b++){s+=mx[b][j]-mx[b][i];if(s<=k) ans++;else break;}}}}cout<<ans;return 0;
}加双指针:
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N =500+10;
int ans = 0;
int k;int mx[N][N]={0};
signed main() {ios::sync_with_stdio(0); cin.tie(0);cout.tie(0);int m,n;cin>>m>>n;cin>>k;//计算每行上的前缀和 for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){cin>>mx[i][j];mx[i][j]+=mx[i][j-1];}}// for(int i=0;i<=n-1;i++){
// for(int j=i+1;j<=n;j++){
//
// 此处 要控制起始行和终点行
// for(int t=1;t<=m;t++){
// int s=0;
// for(int b=t;b<=m;b++){
// s+=mx[b][j]-mx[b][i];
// if(s<=k)
// ans++;
// else break;
// }
// }
//
// }
// }for(int i=0;i<=n-1;i++){for(int j=i+1;j<=n;j++){//t头指针,b尾指针//当和大于k,头指针向右挪动//尾指针最后都要移动for(int t=1,b=1,s=0;t<=m&&b<=m;b++){//int s=0; 应该放在上面初始化为0 s+=mx[b][j]-mx[b][i];while(s>k){s-=mx[t][j]-mx[t][i];t++;} //错误代码,不能加这个判断 ,因为,当t和b都指向一个元素时,这个元素还大于k//s减为0,t移动到b+1位置,并且接下来仍有可能出现小于k的矩阵 //if(t>b) break;/*错误代码,因为此时小于k的矩阵不止一个,而是 b-t+1个即i+1列到j列上,t行到b行的矩阵和小于k,那么,固定t, t到b-1行也小于kt到b-2行也小于k,t到X(t<=X<=b)行都小于k,应该加上t到b的数字个数反过来也一样,b移动到下个位置小于k,将b固定,b行到t行 也是 b-t+1个if(s<=k) {ans++;}*/ans+=b-t+1;}}}cout<<ans;return 0;
}相关文章:

蓝桥杯22年第十三届省赛-统计子矩阵|一维前缀和加双指针
题目链接: 1.统计子矩阵 - 蓝桥云课 (lanqiao.cn) 蓝桥杯2022年第十三届省赛真题-统计子矩阵 - C语言网 (dotcpp.com) 说明: 涉及到子矩阵的时候,一般就跟前缀和相关,可以降维。 先回顾一下最大子矩阵,回忆一下一…...
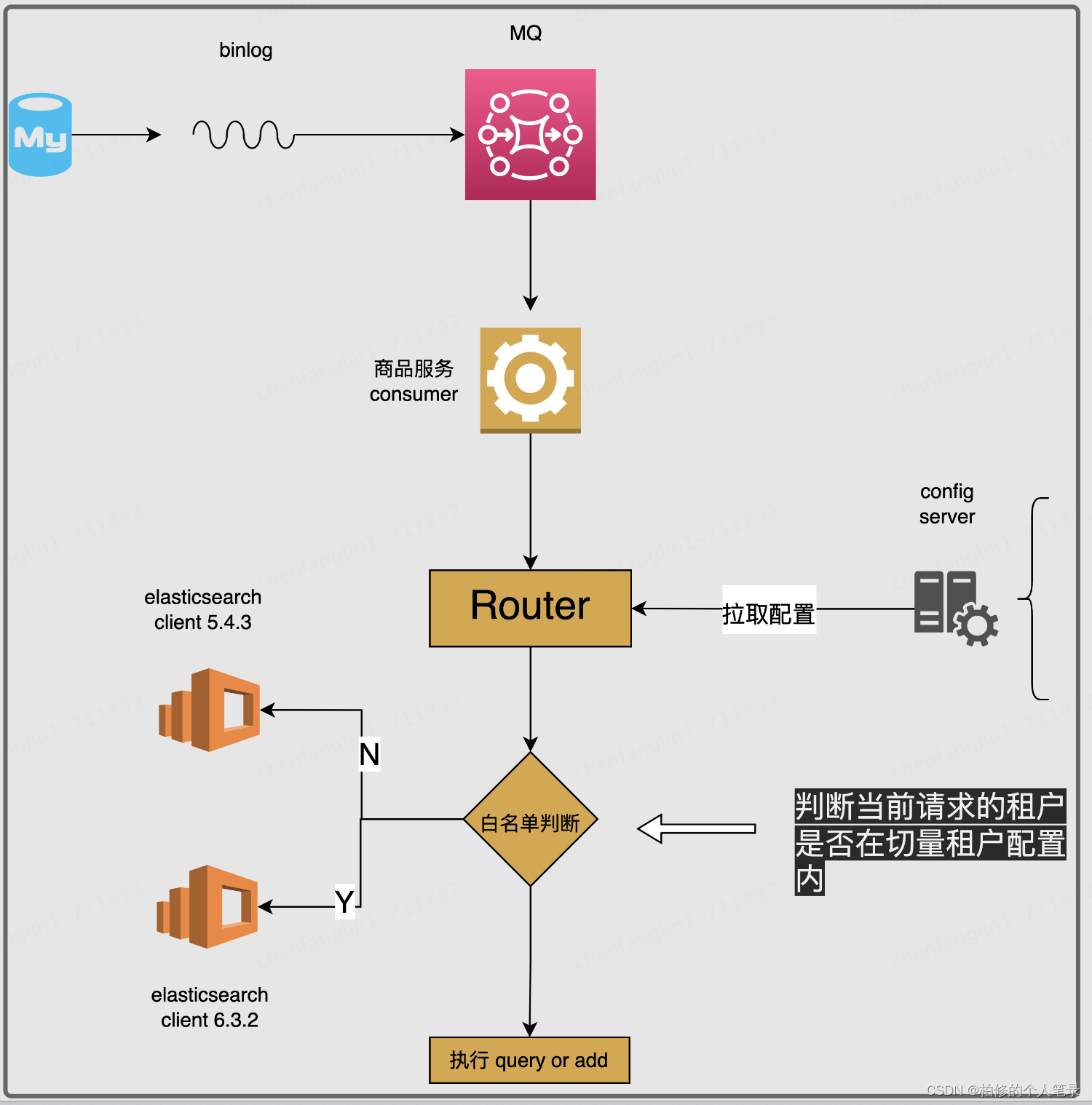
SaaS 电商设计 (十) 记一次 5000kw 商品数据ES迁移 (详细的集群搭建以及线上灰度过程设计)
目录 一.背景二.技术目标三.技术方案3.1 整体流程3.2 ES 切换前:完成整体新集群的搭建.i:拓扑结构设计ii: 如何选择整体的 **ES** 集群配置. 3.3 **ES** 版本切换中3.3.1 多client版本兼容3.3.2 Router的设计 3.4 ES 切换后3.5 开箱即用 四.总结 专栏系列 -SaaS 电商设计 (一) …...
linux安装Tomcat
linux安装Tomcat 下载地址:https://archive.apache.org/dist/tomcat/tomcat-8/v8.5.87/bin/apache-tomcat-8.5.87.tar.gz 将下载的安装包传到该文件夹 解压安装包 tar -zxvf apache-tomcat-8.5.87.tar.gz 配置环境变量 vim /etc/profile 添加指定文件最下方 expo…...

【机器学习300问】57、机器是如何读得懂文本数据的呢?
你知道的,人工智能的大佬们想方设法的让机器具备人一样的能力,比如读懂文本的能力。既然机器是在模仿人类,那么问题“机器是如何读得懂文本数据的呢?”就可以变成“人是如何读得懂文本数据的呢?” 一、人是如何读得懂…...

了解XSS和CSRF攻击与防御
什么是XSS攻击 XSS(Cross-Site Scripting,跨站脚本攻击)是一种常见的网络安全漏洞,它允许攻击者在受害者的浏览器上执行恶意脚本。这种攻击通常发生在 web 应用程序中,攻击者通过注入恶意脚本来利用用户对网站的信任&…...
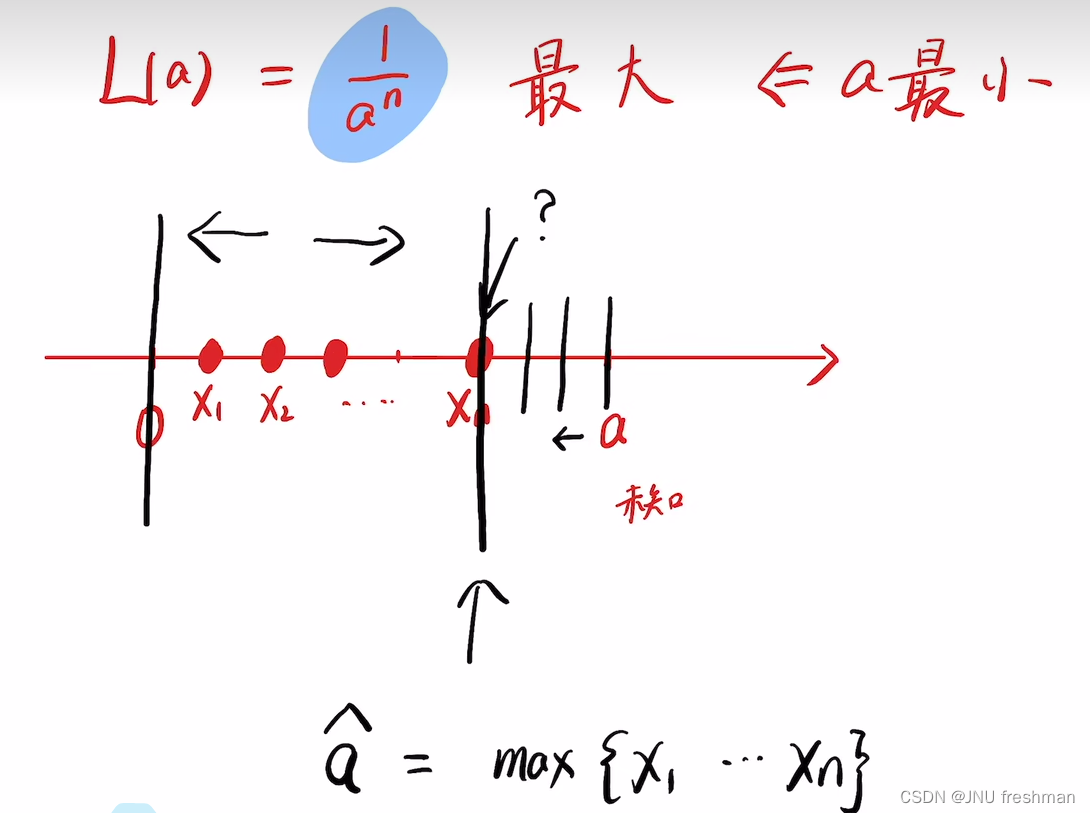
NEO 学习之 MLE(最大似然估计)
文章目录 简单题目MLE 在不同的分布的运用正态分布指数分布均匀分布泊松分布 如何理解 最大似然估计? 就是我们先取出一堆样本,得到一个L( θ \theta θ) 函数,然后的话,这个是关于 θ \theta θ 的一个函数,那么由于存…...

going和Java对比有什么不同
语法风格:Golang 和 Java 的语法风格有很大的不同。Golang 更加简单,语法类似于 C 语言,而 Java 比较复杂,语法类似于 C。 并发:Golang 在并发方面有很大的优势,支持轻量级线程 goroutine 和 channel 通信…...

RabbitMQ面经 手打浓缩版
保证可靠性 生产者 本地事务完成和消息发送同时完成 通过事务消息完成 重写confirm在里面做逻辑处理 确保发送成功(不成功就放入到重试队列) MQ 打开持久化确保消息不会丢失 消费者 改成手动回应 不重复消费 生产者 保证不重复发送消息 消费者…...

JavaScript引用数据类型
JS总共分为两种数据类型: 1.基本数据类型 2.引用数据类型 基本数据类型在之前的文章中待大家了解过了 今天我们就来了解一下引用数据类型: 首先呢,我们要知道引用数据类型是存储在哪里的:引用数据类型是存放在堆内存中的对象…...
Mac m1 Flink的HelloWorld
首先在官方下载Downloads | Apache Flink 下载好压缩包后解压,得到Flink文件夹 进入:cd flink-1.19.0 ls 查看里面的文件: 执行启动集群 ./bin/start-cluster.sh 输出显示它已经成功地启动了集群,并且正在启动 standalonesessio…...

3.1 Python变量的定义和使用
Python变量的定义和使用 任何编程语言都需要处理数据,比如数字、字符串、字符等,我们可以直接使用数据,也可以将数据保存到变量中,方便以后使用。 变量(Variable)可以看成一个小箱子,专门用来…...

OceanBase中左外连接和反连接的经验分享
本文作者:张瑞远,曾从事银行、证券数仓设计、开发、优化类工作,现主要从事电信级IT系统及数据库的规划设计、架构设计、运维实施、运维服务、故障处理、性能优化等工作。 持有Orale OCM,MySQL OCP及国产代表数据库认证。 获得的专业技能与认证…...
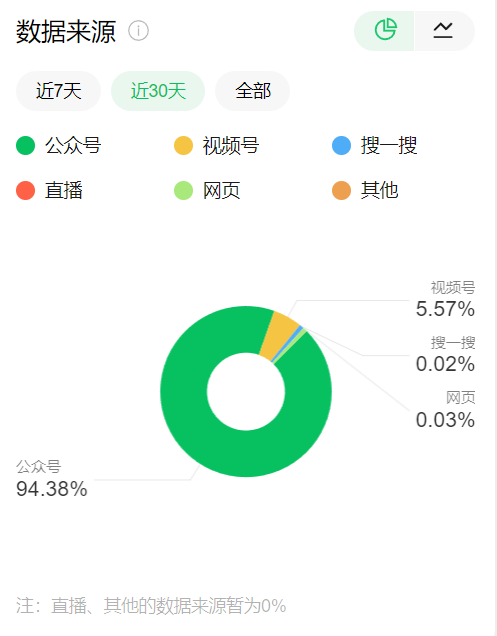
如何提升公众号搜索量?分享内部运营的5步优化技术!
最近一直有自媒体同行朋友在写关于公众号的内容,很多都说公众号现在没得玩了。其实,在运营自媒体上面,思维不通,技术不到位,哪个平台都不适合你玩。 想要在自媒体上面运营变现,一定不要先点击广告变现&…...

【2024】根据系统平均负载情况排查隐患
查看系统负载情况的时候可以使用top和uptime命令。 其中top是一个比较综合的命令,如果我们只需要查看负载情况,可以直接使用uptime命令即可。 uptime命令是一个查看系统运行时间和负载情况的命令,分为四个部分: 系统当前时间系统运行时间当前登录用户数系统平均负载:分别…...
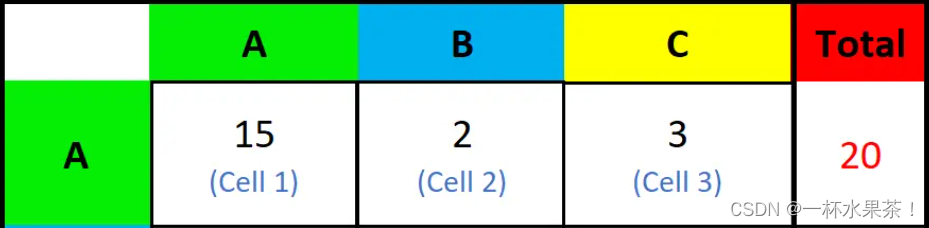
分类任务中的评估指标:Accuracy、Precision、Recall、F1
概念理解 T P TP TP、 T N TN TN、 F P FP FP、 F N FN FN精度/正确率( A c c u r a c y Accuracy Accuracy) 二分类查准率 P r e c i s i o n Precision Precision,查全率 R e c a l l Recall Recall 和 F 1 − s c o r e F1-score F1−s…...

android 音视频基础知识--个人笔记
avi,mkv封装格式数据------》音频流,视频流//字母流(国外会分开) ----〉解封装,解复用打开封装格式 -----》视频压缩数据---压缩H264,H265 -------〉视频解码 ----》原始数据YUV -----〉音频压缩数据---…...
信息工程大学第五届超越杯程序设计竞赛(同步赛)题解
比赛传送门 博客园传送门 c 模板框架 #pragma GCC optimize(3,"Ofast","inline") #include<bits/stdc.h> #define rep(i,a,b) for (int ia;i<b;i) #define per(i,a,b) for (int ia;i>b;--i) #define se second #define fi first #define e…...

Python:文件读写
一、TXT文件读写 Python中用open()函数来读写文本文件,返回文件对象,以下是函数语法。 open(<name>, <mode>, <buffering>,<encoding)name:文件名。 mode:打开文件模式。 buffering:设…...

10.windows ubuntu 组装软件:spades,megahit
Spades 是一种用于组装测序数据的软件,特别适用于处理 Illumina 测序平台产生的数据。它的全称是 "St. Petersburg genome assembler",是一款广泛使用的基因组组装工具。 第一种:wget https://cab.spbu.ru/files/release3.15.3/S…...

K8S之Secret的介绍和使用
Secret Secret的介绍Secret的使用通过环境变量引入Secret通过volume挂载Secret Secret的介绍 Secret是一种保护敏感数据的资源对象。例如:密码、token、秘钥等,而不需要把这些敏感数据暴露到镜像或者Pod Spec中。Secret可以以Volume或者环境变量的方式使…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

day51 python CBAM注意力
目录 一、CBAM 模块简介 二、CBAM 模块的实现 (一)通道注意力模块 (二)空间注意力模块 (三)CBAM 模块的组合 三、CBAM 模块的特性 四、CBAM 模块在 CNN 中的应用 一、CBAM 模块简介 在之前的探索中…...
加密芯片与MCU协同工作的典型流程)
SE(Secure Element)加密芯片与MCU协同工作的典型流程
以下是SE(Secure Element)加密芯片与MCU协同工作的典型流程,综合安全认证、数据保护及防篡改机制: 一、基础认证流程(参数保护方案) 密钥预置 SE芯片与MCU分别预置相同的3DES密钥(Key1、Key2…...
[KCTF]CORE CrackMe v2.0
这个Reverse比较古老,已经有20多年了,但难度确实不小。 先查壳 upx压缩壳,0.72,废弃版本,工具无法解压。 反正不用IDA进行调试,直接x32dbg中,dump内存,保存后拖入IDA。 这里说一下…...

OCC笔记:TDF_Label中有多个相同类型属性
注:OCCT版本:7.9.1 TDF_Label中有多个相同类型的属性的方案 OCAF imposes the restriction that only one attribute type may be allocated to one label. It is necessary to take into account the design of the application data tree. For exampl…...

CSS(2)
文章目录 Emmet语法快速生成HTML结构语法 Snipaste快速生成CSS样式语法快速格式化代码 快捷键(VScode)CSS 的复合选择器什么是复合选择器交集选择器后代选择器(重要)子选择器(重要)并集选择器(重要)**链接伪类选择器**focus伪类选…...
