保研线性代数机器学习基础复习2
1.什么是群(Group)?
对于一个集合 G 以及集合上的操作 ,如果G
G-> G,那么称(G,
)为一个群,并且满足如下性质:
- 封闭性:

- 结合性:

- 中性元素:

- 逆元素:

2.什么是阿贝尔群(Abelian group)?
满足交换(commutative)特征的群,称为阿贝尔群。
 3.(
3.(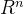 ,+)和(
,+)和(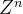 ,+)是阿贝尔群吗?说明理由。
,+)是阿贝尔群吗?说明理由。
- 满足封闭性:

- 满足结合性
- 中性元素是:
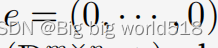
- 逆元素是:

- 满足交换性
4.(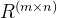 ,+)是阿贝尔群吗?
,+)是阿贝尔群吗?
是
5.什么是一般线性群(general linear group)?
讨论(,*)可逆/正则/非奇异方阵以及关于方阵的multiply的操作,是群,但是不是阿贝尔群,因为矩阵乘法不满足交换性。
- 封闭性和结合性同一般矩阵
- 中性元素:单位矩阵
- 逆元素:对于任意矩阵其逆元素是它的逆矩阵
6.什么是实数向量空间/线性空间(vector space)?
对于向量空间V=(V,+,*)拥有两种操作:
- +:V操作V得到V (是向量的add操作,每两个向量的逐个元素相加)
- *:实数R操作V得到V (是标量乘法scale操作,用向量乘以标量)
同时满足下列条件:
- (V,+)是一个阿贝尔群
- 分配性:

- 结合性:

- 中性元素:1(对于*,因为+是阿贝尔群)
7.举例一些常见的线性空间?
- n维向量空间

- m行n列矩阵

- 复数域可以看做是实数域上的线性空间

8.什么是向量子空间(Vector Subspace)?
如果向量空间,并且
,并且U也是满足add和scale的向量空间。
例如齐次线性方程组![]() 的解
的解是Rn的向量子空间,但是非齐次线性方程组
![]() 的解就不是Rn的子空间。任何一个Rn的子空间都是齐次线性方程组的解。
的解就不是Rn的子空间。任何一个Rn的子空间都是齐次线性方程组的解。
9.什么是线性组合(Linear Combination)?
首先考虑向量空间V,,
,有
 称
称是向量
的线性组合。
10.什么是线性无关(Linear Independent)?
考虑一个向量空间V,其中![]() ,如果存在线性组合满足
,如果存在线性组合满足![]() ,其中至少一个λ!=0,那么说明
,其中至少一个λ!=0,那么说明线性相关(Linear dependent),但是如果仅仅存在所有
,那么说明
线性无关(Linear Independent)。
11.寻找线性无关向量的方法?
- 首先要确定的是k个向量要么线性无关,要么线性相关,不可能存在第三种情况
- 如果至少一个向量
是0向量,那么他们一定线性相关。如果两个向量,并且他们相同,那么也一定线性相关。
- 如果其中一个向量xi是另一个向量xj的倍数,或者其中一个向量x可以由其他向量线性表示
- 使用高斯消元法对
进行消元,初等变换成列向量之后,如果所有列向量都是pivot column,那么这k个线性无关,如果存在至少一个non-pivot column,那么说明这k个列向量线性相关。
12.如果m>k,那么x1,...,xm线性相关

相关文章:

保研线性代数机器学习基础复习2
1.什么是群(Group)? 对于一个集合 G 以及集合上的操作 ,如果G G-> G,那么称(G,)为一个群,并且满足如下性质: 封闭性:结合性:中性…...
vultr ubuntu 服务器远程桌面安装及连接
一. 概述 vultr 上开启一个linux服务器,都是以终端形式给出的,默认不带 ui 桌面的,那其实对于想使用服务器上浏览器时的情形不是很好。那有没有方法在远程服务器安装桌面,然后原程使用呢?至少ubuntu的服务器是有的&am…...
前端学习<二>CSS基础——12-CSS3属性详解:动画详解
前言 本文主要内容: 过渡:transition 2D 转换 transform 3D 转换 transform 动画:animation 过渡:transition transition的中文含义是过渡。过渡是CSS3中具有颠覆性的一个特征,可以实现元素不同状态间的平滑过渡…...
Sqoop 的安装与配置
目录 1 下载并解压2 修改配置文件3 添加环境变量4 拷贝 JDBC 驱动5 测试Sqoop是否能够成功连接数据库 下载地址 1 下载并解压 (1)上传安装包 sqoop-1.4.6.bin__hadoop-2.0.4-alpha.tar.gz 到 hadoop101 的 /opt/software 路径中 (2…...

Mysql设置访问权限(docker配置)
1.运行命令:docker exec -it 数据库名 bash,我这里是bot_test, docker exec -it bot_test bash 2.运行命令mysql -uroot -p --default-character-setutf8,输入密码连接数据库 3.运行命令show databases,查看当前的表 4.进入my…...
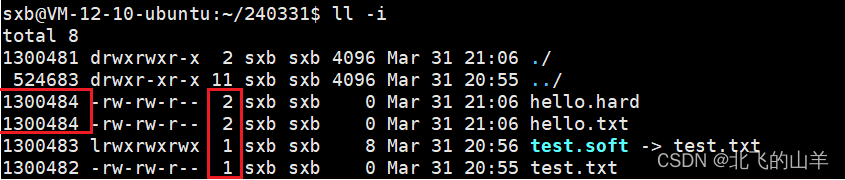
【Linux】详解软硬链接
一、软硬链接的建立方法 1.1软链接的建立 假设在当前目录下有一个test.txt文件,要对其建立软链接,做法如下: ln就是link的意思,-s表示软链接,test.txt要建立软链接的文件名,后面跟上要建立的软链接文件名…...

维修贝加莱4PP420.1043-B5触摸屏Power Panel 400工业电脑液晶
深圳捷达工控维修为贝加莱、HMI 显示电源面板 400 4PP420.1043-B5 提供专业电子维修。在 深圳捷达工控维修,我们拥有及时且经济高效地维修 B&R 、HMI Display Power Panel 400 4PP420.1043-B5 的经验。我们为发送给我们工厂维修的贝加莱 HMI 显示面板 400 4PP42…...
Java_21 完成一半题目
完成一半题目 有 N 位扣友参加了微软与力扣举办了「以扣会友」线下活动。主办方提供了 2*N 道题目,整型数组 questions 中每个数字对应了每道题目所涉及的知识点类型。 若每位扣友选择不同的一题,请返回被选的 N 道题目至少包含多少种知识点类型。 示例…...

【WPF应用21】WPF 中的 TextBox 控件详解与示例
在 Windows Presentation Foundation (WPF) 中,TextBox 控件是一个强大的输入控件,允许用户输入、编辑和选择文本。TextBox 控件在各种应用程序中都非常常见,例如表单、对话框和编辑器。本文将详细介绍 TextBox 控件的功能、使用方法、属性、…...

小程序页面传参?
小程序页面之间传递参数通常可以通过以下几种方式实现: 通过 URL 参数传递:可以在跳转目标页面时,在 URL 中添加参数,目标页面可以通过 options 参数获取传递过来的数据。 // 页面 A wx.navigateTo({url: targetPage?param1value…...
C++list的模拟实现
为了实现list,我们需要实现三个类 一、List的节点类 template<class T> struct ListNode {ListNode(const T& val T()):_pPre(nullptr),_pNext(nullptr),_val(val){}ListNode<T>* _pPre;ListNode<T>* _pNext;T _val; }; 二、List的迭代器…...

Leetcode 187. 重复的DNA序列
DNA序列 由一系列核苷酸组成,缩写为 ‘A’, ‘C’, ‘G’ 和 ‘T’.。 例如,“ACGAATTCCG” 是一个 DNA序列 。 在研究 DNA 时,识别 DNA 中的重复序列非常有用。 给定一个表示 DNA序列 的字符串 s ,返回所有在 DNA 分子中出现不…...
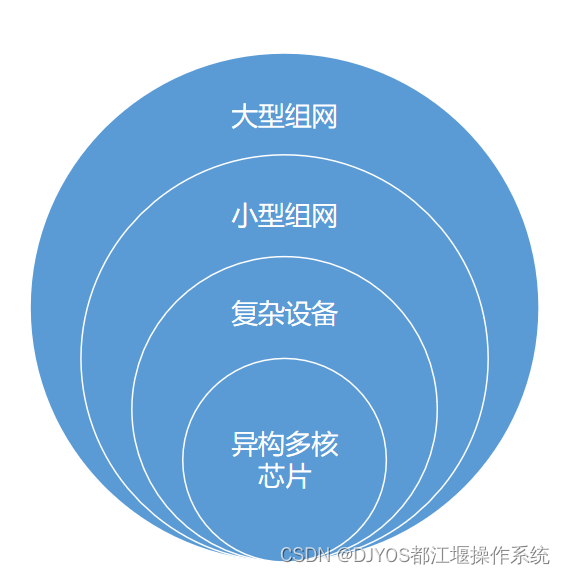
都江堰泛计算操作系统(多机)应用方向
1、异构多核芯片 DJYOS是全球唯一支持异构多核的操作系统。当前的系统级芯片,为了适应多样化的用户需求,基本上都采用了异构多核架构。传统操作系统就需要在一个芯片内,运行多种操作系统,开发工作更加复杂,运行协同性低…...

【第十二届“泰迪杯”数据挖掘挑战赛】【2024泰迪杯】B题基于多模态特征融合的图像文本检索—解题全流程(论文更新)
【第十二届“泰迪杯”数据挖掘挑战赛】【2024泰迪杯】B题基于多模态特征融合的图像文本检索更新(论文更新) 本节主要更新了论文、训练日志的log数据提取(Loss、ACC、RK)等数据可视化作图的代码 B题交流QQ群: 4583…...

蓝桥杯22年第十三届省赛-统计子矩阵|一维前缀和加双指针
题目链接: 1.统计子矩阵 - 蓝桥云课 (lanqiao.cn) 蓝桥杯2022年第十三届省赛真题-统计子矩阵 - C语言网 (dotcpp.com) 说明: 涉及到子矩阵的时候,一般就跟前缀和相关,可以降维。 先回顾一下最大子矩阵,回忆一下一…...
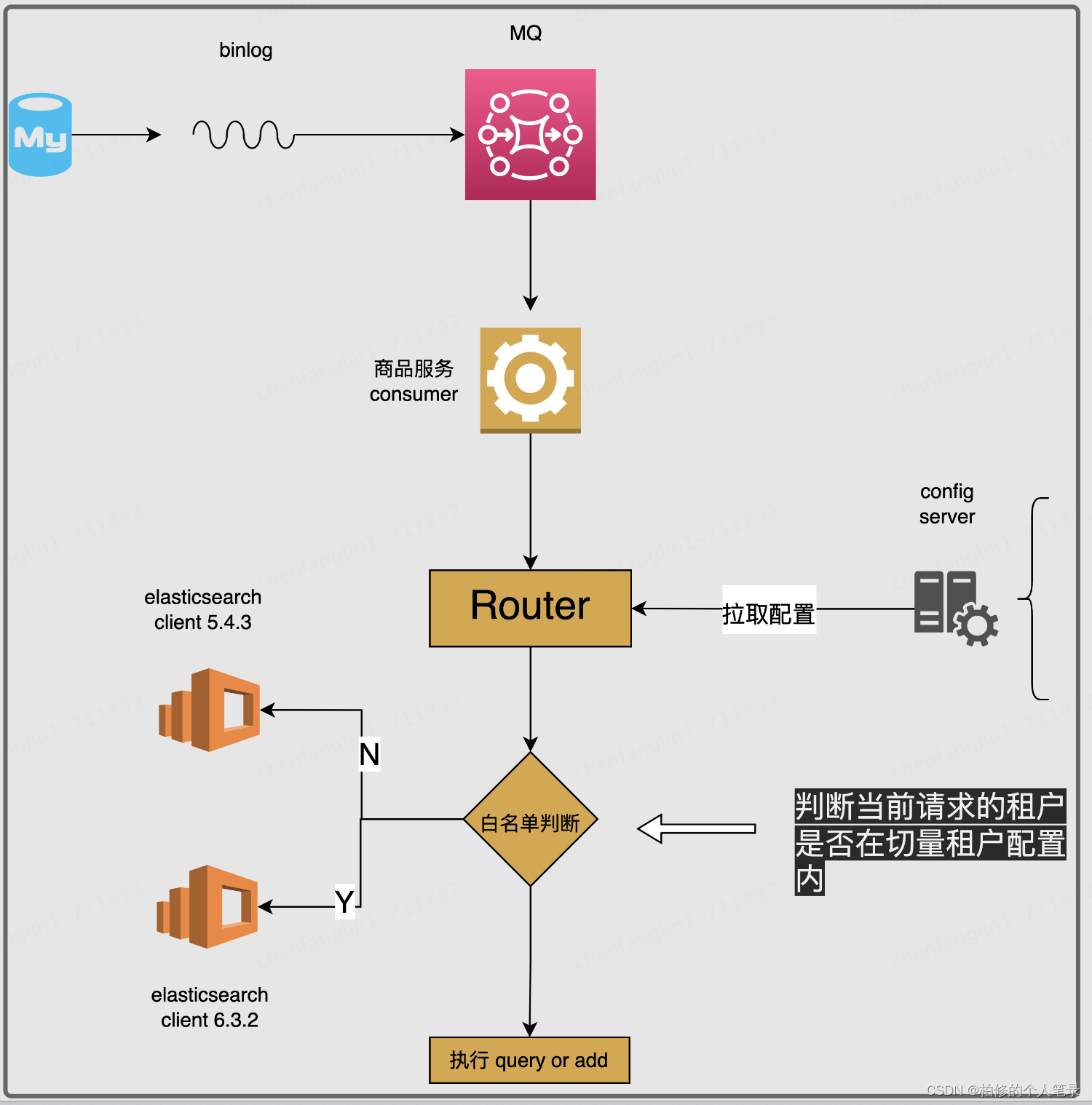
SaaS 电商设计 (十) 记一次 5000kw 商品数据ES迁移 (详细的集群搭建以及线上灰度过程设计)
目录 一.背景二.技术目标三.技术方案3.1 整体流程3.2 ES 切换前:完成整体新集群的搭建.i:拓扑结构设计ii: 如何选择整体的 **ES** 集群配置. 3.3 **ES** 版本切换中3.3.1 多client版本兼容3.3.2 Router的设计 3.4 ES 切换后3.5 开箱即用 四.总结 专栏系列 -SaaS 电商设计 (一) …...
linux安装Tomcat
linux安装Tomcat 下载地址:https://archive.apache.org/dist/tomcat/tomcat-8/v8.5.87/bin/apache-tomcat-8.5.87.tar.gz 将下载的安装包传到该文件夹 解压安装包 tar -zxvf apache-tomcat-8.5.87.tar.gz 配置环境变量 vim /etc/profile 添加指定文件最下方 expo…...

【机器学习300问】57、机器是如何读得懂文本数据的呢?
你知道的,人工智能的大佬们想方设法的让机器具备人一样的能力,比如读懂文本的能力。既然机器是在模仿人类,那么问题“机器是如何读得懂文本数据的呢?”就可以变成“人是如何读得懂文本数据的呢?” 一、人是如何读得懂…...

了解XSS和CSRF攻击与防御
什么是XSS攻击 XSS(Cross-Site Scripting,跨站脚本攻击)是一种常见的网络安全漏洞,它允许攻击者在受害者的浏览器上执行恶意脚本。这种攻击通常发生在 web 应用程序中,攻击者通过注入恶意脚本来利用用户对网站的信任&…...
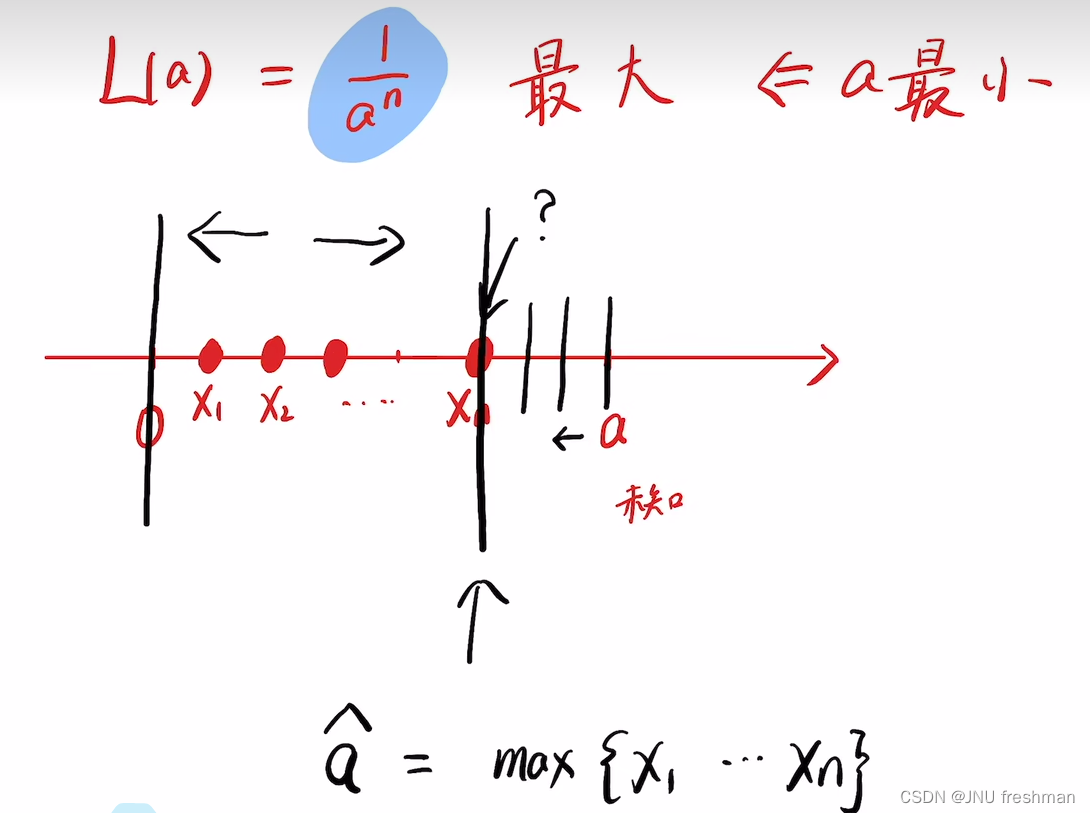
NEO 学习之 MLE(最大似然估计)
文章目录 简单题目MLE 在不同的分布的运用正态分布指数分布均匀分布泊松分布 如何理解 最大似然估计? 就是我们先取出一堆样本,得到一个L( θ \theta θ) 函数,然后的话,这个是关于 θ \theta θ 的一个函数,那么由于存…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
