《拆解一切问题》如何成为解决难题的高手 - 三余书屋 3ysw.net

拆解一切问题:如何成为解决难题的高手
今天给大家分享的这本书叫做《拆解一切问题》,标题看起来确实有点虚,在没有读这本书之前,会让人感觉似乎只要读完学会书中的内容,就可以解决一切问题了。但事实上这种认识是误解,并没有什么问题的解决可以采用通用的方法。不过,作者在文中聊到的一些方法还是有很多值得学习和参考的。对于我们来说,看一本书就只要看其有用的部分,能够有所启发的某个知识点,哪怕是用某个关键词就可以了,并不需要全盘接受作者的观点。如果读完这本书对你自己的生活或者解决问题有帮助的话,那么就没有白读。下面我具体为大家来聊聊本书的重点内容。
思维才是解决问题的关键武器,作者将解决问题的思维非常形象地描述出来,也就是本书中的五大章节的标题:尺子思维、剪刀思维、针线思维、锤子思维和螺丝刀思维。这五大思维的作用就是对问题边界的丈量、分割杂糅问题、链接碎片化问题、实锤疏忽问题和让拆解成为习惯。现在就让我们一一来看一下这五种思维。
第一种,锁定问题,尺子思维,丈量问题的边界。遇到一个问题,首先想到的是区分问题的类型,如果是疑问,那肯定会有正确答案,如果你还不知道,那可能只是知识面的问题。如果是难题,那就应该第一时间想到,没有什么标准答案,有的只是通过采取必要的行动推进事情顺利的解决方案,而解决方案没有对错之分,只有优劣之分。看似简单,可是会解决问题的人和不会解决问题的人之间的根本性区别在于,理解问题的角度不同。不会解决问题的人止步于调查,会解决问题的人致力于思考。作者提出了一个五步高效流程:觉察问题出现的征兆,锁定问题改善之处,筛选解题路径、解决方案的适应性,积极评估改进效果。
第二种,剪刀思维分割杂糅问题,遇到一个难题,为什么常常无法下手呢?因为问题太笼统,无从下手。怎么做呢?可以考虑采用剪刀思维,首先抓住问题的关键词进行分析,也就是将问题大卸八块后重新建构。具体的操作思路就是使用某种逻辑先将问题拆分,然后再使用另一种逻辑进行整合。当下已经有很多成熟的分解结构,比如工作中常见的分解结构,包括工作分解结构(简称WBS)、组织分解结构(简称OBS)、项目分解结构(简称PBS)等。
第三种,针线思维链接碎片化问题,灵感往往在一瞬间迸发,但前提是需要有一定的知识储备和积累。历史上就发生过一个活生生的例子,有一年发生饥荒,百姓没有粮食吃,只有挖草根吃树皮,许多百姓因此活活饿死,消息被迅速报到了皇宫中。晋惠帝坐在高高的皇座上,听完了大臣的奏报后,大为不解。善良的晋惠帝很想为他的子民做点事情,经过冥思苦想后,终于悟出了一个解决方案:“百姓无粟米,何不食肉糜?”众人看来确实是片面好笑的办法,但是站在只知道酒肉、不知道草根树皮这些知识的晋惠帝来说,这只能是他所想到的最好的办法了吧。
那如何来解决这种问题,避免再产生贻笑大方的事情呢?那就是创新。书中提到了头脑风暴法、检核表法、类比思考法,借助工具将碎片化的灵感串联起来,逐渐找到解决问题的更好的方案。第四种,锤子思维,实锤疏忽问题。经构思得到的解决方案必然以适宜的形式回到实践中去,经过再次耐心的审视和推敲,才能最终得以确定。这个过程就是我们所说的锤炼。铁矿,经过不断的锤炼,才能将有害气体与不纯物质去除,正是因为有了这样的过程,才能炼成强韧的钢。构想和创意也是如此,必须经过反复打磨和推敲,才能删除其中的有害成分和不利因素。最终,我们将获得像钢一样有韧性的思维,并将初步构想打磨成高效的解决方案。
运用创新思维学之父爱德华·德博诺(Edward de Bono)博士开发的六顶思考帽思考法,会使混乱的思考变得更清晰,使团体中无意义的争论变成集思广益的探讨,使每个人变得富有创造性。整个过程不是无休止的争论,而是集思广益。第五种,螺丝刀思维,拧紧大脑的发条,让拆解成为一种习惯。只要在解决问题的过程中,经过分析、创构、锤炼这三个步骤,即使对于非常棘手的问题,我们也能够构思出巧妙的解决方案。单独解决一次问题可能会让你获得奖赏,但并不能让你真正成长。学会持续解决身边的问题,才能更好地促进自身成长,更好地体会达成目标的成就感。这就需要有一种螺丝刀思维,通过刻意练习、分析、创构、锤炼三个步骤,让自己修炼成为一名解决问题的高手。刻意练习、写道,学习不再是挖掘某人潜力的方式,而是开发这种潜力的方式。我们可以创造自己的潜力,拆解一切问题的最后一步就是刻意练习,让拆解成为一种习惯。要知道,如果每天努力1%,有的人在此基础上多努力1%,那么不久就会产生巨大的力量。而如果偷懒1%,则很容易失去竞争力。
学会了解这五种思维后,我们该如何有逻辑地拆解一切问题呢?按作者的思维方法,我们来自己总结一下,其实拆解问题的方法有四种:结构性思维、系统性思维、公式思维、假设思维。当你能知道复杂问题里的影响元素时,就用结构性思维、系统性思维、公式思维。当你不知道时,就用假设思维。下面我们分别来说这三种思维方式。
什么是结构性思维?结构性思维相对系统性思维是静态的。当你遇到一个复杂问题时,把问题拆分为影响问题的元素A、B、C,其中影响A的元素又需要拆分为A1、A2、A3,就这样一直拆分,直到把复杂的问题拆分成若干个可解决的原问题。拆分的过程需要遵循麦肯锡的MECE法则,相互独立,完全穷尽。这个法则是拆分的精髓,不懂法则就无法拆分。
拆分后需要不断问自己还有遗漏的元素吗?这些元素之间是相互独立的吗?某两个元素是否有重合的嫌疑?这个问题拆分后就得出了最佳的答案,你会根据自己的资源和时间,知道先做什么、后做什么、不做什么而不断调整,最终找到最优解。当发现影响复杂问题的元素A、B、C是相互独立的时候,用结构性思维。什么是系统性思维?系统性思维就是搭建模型。系统性思维相对结构性思维是动态的,是一组相互连接的要素,相互作用是系统决定了个体要素的行为。一个系统的组成要素就是结构性思维的元素,连接功能偏生物或目标偏人类。其中连接是要素间的关系,分四种:因果链、增强回路、调节回路和滞后效应。要素在这四种连接关系的作用下也会持续变化,这时候被赋予了一个新名字:变量。实操中,一个复杂问题如何开好一家咨询公司?在这借用刘润老师的创业系统图,他先是找到能带来收入的核心元素,声誉是元素,也是变量,再找到影响声誉的两大要素:作品和学识。好的作品提升个人的声誉,声誉的提升能让他获得企业的信任,有机会为知名企业提供咨询实践的成功案例,提升了学识的提升,行程作品提升声誉,最终形成一个增强回路,不断滚雪球。
当发现影响复杂问题的元素A、B、C是相互影响时,若A加强或者减弱了B,B加强或者减弱了C,C加强或者减弱了A的时候,就用系统性思维,它能持续地指引你在正确的道路上努力。什么是公式思维?把复杂问题的解答方式公式化,就是公式思维。公式思维可以清晰地呈现各要素增强或者减弱后是如何作用于复杂问题的形式,如问题Z等于A加B加C,问题Z等于X,quit问题Z等于AB乘以Z,问题Z等于A加B减C。诸如此类的算术形式、公式思维还可以解决一些类似某个城市有多少自行车,这个城市的地铁一天多少人次这样的变态问题。
一个麦肯锡的人被叫到谷歌,给到的任务是提升广告部门的收入,这还是个复杂问题,不可被直接解决。那他是怎么做的?他叫上了广告部门的人,问道:“你们的任务公式是什么?”部门的人呆了,说我们从来都没有过什么公式。最终在讨论下,他们得出了一个业务公式:广告收入等于曝光量乘以点击率乘以每次点击的单价。你会发现,提高广告部的收入有三种办法:提高广告的曝光量、点击率和每次点击的单价。
当发现影响复杂问题的元素A、B、C相互独立,且各要素的增强或者减弱以某种数学关系在影响复杂问题时,可以用公式思维。最后说明一下,或许每个人读完的收获都会不一样,但是从本书我们依然可以发现,其实解决一切问题的关键还在于思维方式和方法。原则上,只要你能够运用每种思维方法,就能够很轻松地面对和解决生活中的各类问题。
————————————————
本文为[三余书屋]收集和整理,原文链接:https://www.3ysw.net/book/1768048822730723328
相关文章:

《拆解一切问题》如何成为解决难题的高手 - 三余书屋 3ysw.net
拆解一切问题:如何成为解决难题的高手 今天给大家分享的这本书叫做《拆解一切问题》,标题看起来确实有点虚,在没有读这本书之前,会让人感觉似乎只要读完学会书中的内容,就可以解决一切问题了。但事实上这种认识是误解…...

matlab——基于三维激光扫描点云的树冠体积计算方法
目录 一、算法原理1、原理概述2、参考文献二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT。 一、算法原理 1、原理概述 针对树冠形状不规则,树冠体积难以测量和计算的问题,提出一种基于三…...
如何在jupyter使用新建的虚拟环境以及改变jupyter启动文件路径。
对于刚刚使用jupyter的新手来说,经常不知道如何在其中使用新建的虚拟环境内核,同时,对于默认安装的jupyter,使用jupyter notebook命令启动 jupyter 以后往往默认是C盘的启动路径,如下图所示,这篇教程将告诉…...
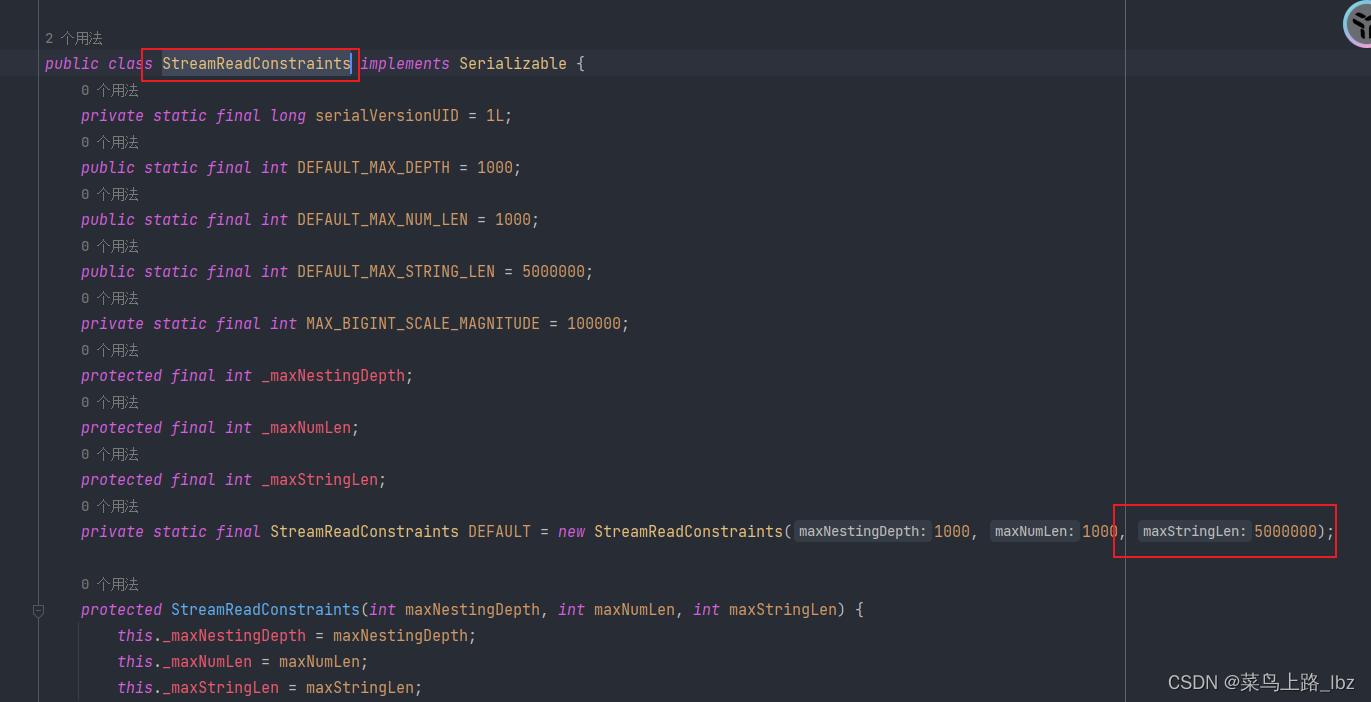
Exception in thread “main“ com.fasterxml.jackson.databind.JsonMappingException:
问题:jaskson反序列化超出最大长度 Caused by: com.fasterxml.jackson.core.exc.StreamConstraintsException: String length (5043456) exceeds the maximum length (5000000) 场景:前端传递过大base64 原因: jaskon默认已经限制了最大长…...

第三十九章 保护与 IRIS 的 Web 网关连接
文章目录 第三十九章 保护与 IRIS 的 Web 网关连接配置 Web 网关的连接安全最低连接安全性(不推荐)简单的用户名/密码验证 第三十九章 保护与 IRIS 的 Web 网关连接 本页介绍用于保护从 Web Gateway 到 IRIS 的连接的选项。与 IRIS 的 Web 网关连接可以…...
java数据结构与算法刷题-----LeetCode127. 单词接龙
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 文章目录 广度优先双分裂蛇 广度优先双分裂蛇 解题思路:时间复…...

pytorch中的torch.nn.Linear
torch.nn.Linear是pytorch中的线性层,应该是最常见的网络层了,官方文档:torch.nn.Linear。 torch.nn.Linear(in_features, out_features, biasTrue, deviceNone, dtypeNone)其中,in_features表示输入的维度;out_featu…...

03-MySQl数据库的-用户管理
一、创建新用户 mysql> create user xjzw10.0.0.% identified by 1; Query OK, 0 rows affected (0.01 sec) 二、查看当前数据库正在登录的用户 mysql> select user(); ---------------- | user() | ---------------- | rootlocalhost | ---------------- 1 row …...
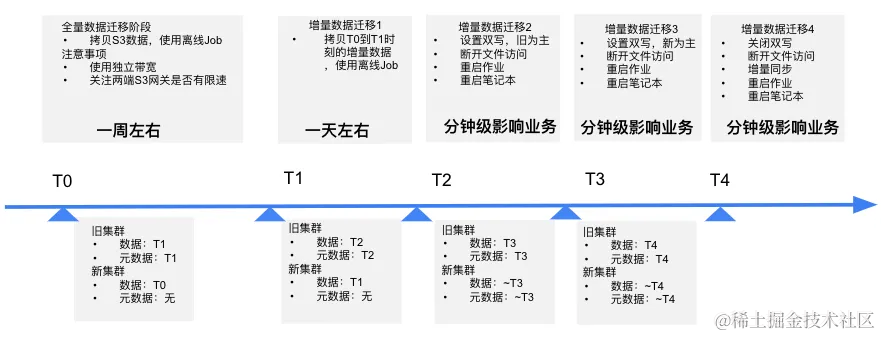
知乎:多云架构下大模型训练,如何保障存储稳定性?
知乎,中文互联网领域领先的问答社区和原创内容平台,2011 年 1 月正式上线,月活跃用户超过 1 亿。平台的搜索和推荐服务得益于先进的 AI 算法,数百名算法工程师基于数据平台和机器学习平台进行海量数据处理和算法训练任务。 为了提…...
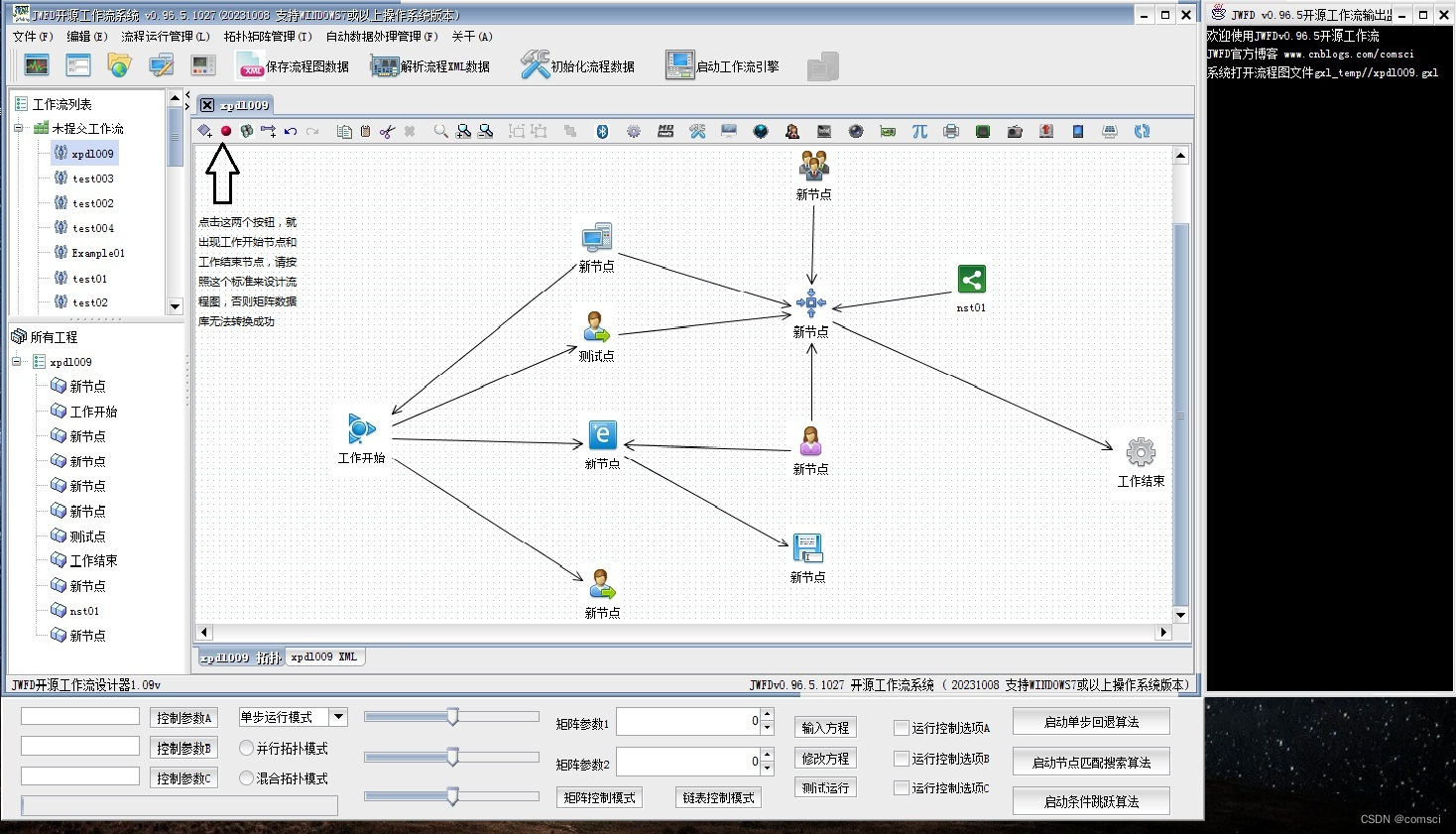
JWFD流程图转换为矩阵数据库的过程说明
在最开始设计流程图的时候,请务必先把开始节点和结束节点画到流程图上面,就是设计器面板的最开始两个按钮,先画开始点和结束点,再画中间的流程,然后保存,这样提交到矩阵数据库就不会出任何问题,…...
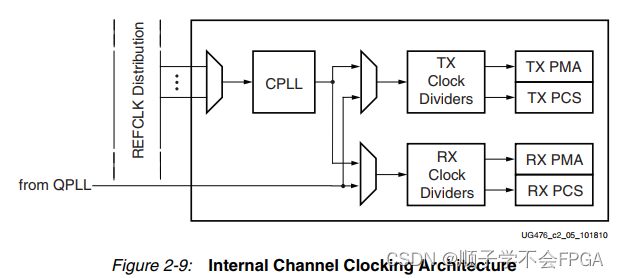
GT收发器第一篇_总体结构介绍
文章目录 前言GT收发器介绍 前言 之前写过一篇简单介绍GT的文章https://blog.csdn.net/m0_56222647/article/details/136730026,可以先通过这篇文章对整体进行简单了解一下。 GT收发器介绍 参考xilinx手册ug476 对于7系列的FPGA,共有3个系列…...
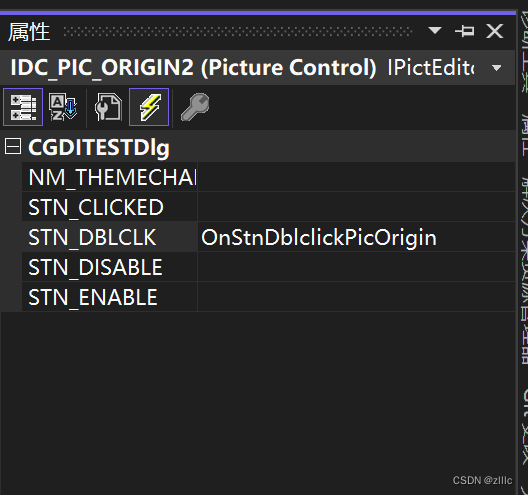
[图像处理] MFC载入图片并进行二值化处理和灰度处理及其效果显示
文章目录 工程效果重要代码完整代码参考 工程效果 载入图片,并在左侧显示原始图片、二值化图片和灰度图片。 双击左侧的图片控件,可以在右侧的大控件中,显示双击的图片。 初始画面: 载入图片: 双击左侧的第二个控件…...
)
centos7.5 安装gitlab-ce (Omnibus)
一、安装前置依赖 # 安装基础依赖 $ sudo yum -y install policycoreutils openssh-server openssh-clients postfix# 启动 ssh 服务 & 设置为开机启动 $ sudo systemctl enable sshd & sudo systemctl start sshd二、安装gitlab rpm包 # 下载并执行社区版脚本 curl …...
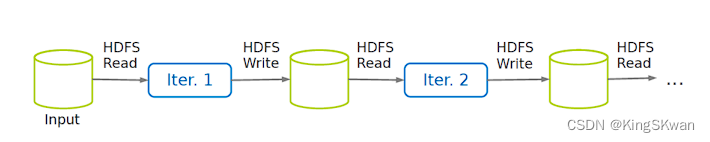
深入理解MapReduce:从Map到Reduce的工作原理解析
当谈到分布式计算和大数据处理时,MapReduce是一个经典的范例。它是一种编程模型和处理框架,用于在大规模数据集上并行运行计算任务。MapReduce包含三个主要阶段:Map、Shuffle 和 Reduce。 ** Map 阶段 ** Map 阶段是 MapReduce 的第一步&am…...
初始Java篇(JavaSE基础语法)(5)(类和对象(上))
个人主页(找往期文章包括但不限于本期文章中不懂的知识点):我要学编程(ಥ_ಥ)-CSDN博客 目录 面向对象的初步认知 面向对象与面向过程的区别 类的定义和使用 类的定义格式 类的实例化 this引用 什么是this引用? this引用…...

机器人---人形机器人之技术方向
1 背景介绍 在前面的文章《行业杂谈---人形机器人的未来》中,笔者初步介绍了人形机器人的未来发展趋势。同智能汽车一样,它也会是未来机器人领域的一个重要分支。目前地球上最高智慧的结晶体就是人类,那么人形机器人的未来会有非常大的发展空…...
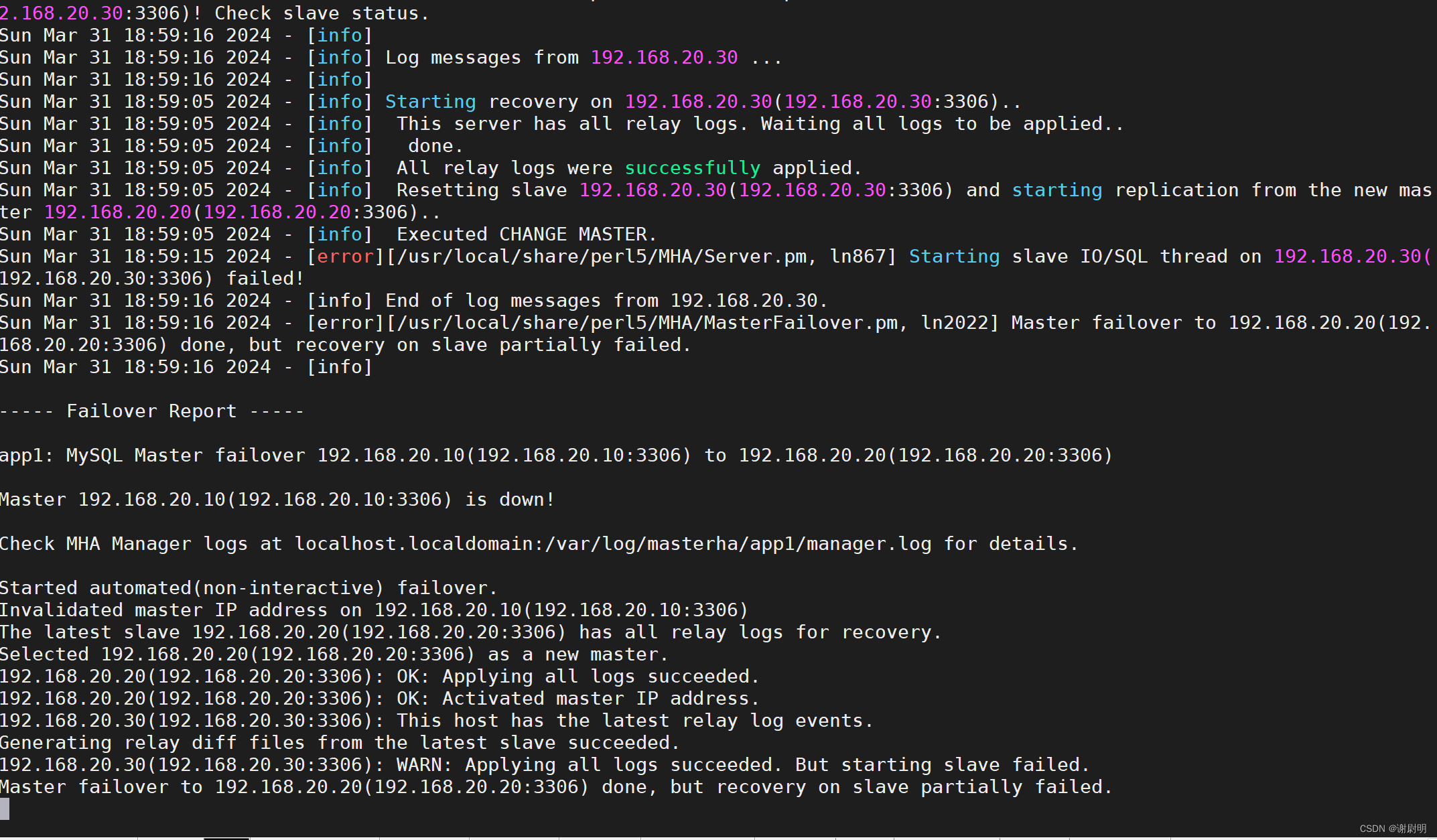
MySQL MHA高可用数据库
文章目录 MySQL MHA高可用数据库搭建MySQL MHA模拟故障故障修复: MySQL MHA高可用数据库 MHA(MySQL High Availability)是一个开源的高可用解决方案,用于实现MySQL主从复制集群的故障自动切换。MHA的主要目的是确保MySQL数据库集…...
比的是什么?)
LVS(Layout versus schematic)比的是什么?
概述 LVS不是一个简单地将版图与电路原理图进行比较的过程,它需要分两步完成。第一步“抽取”,第二步“比较”。首先根据LVS提取规则,EDA 工具从版图中抽取出版图所确定的网表文件;然后将抽取出的网表文件与电路网表文件进行比较…...
从0开始搭建基于VUE的前端项目(三) Vuex的使用与配置
准备与版本 vuex 3.6.2(https://v3.vuex.vuejs.org/zh/)概念 vuex是什么? 是用作 【状态管理】的 流程图如下 state 数据状态,成员是个对象 mapState 组件使用this.$store.state.xxx获取state里面的数据 getters 成员是个函数,方便获取state里面的数据,也可以加工数据 ma…...
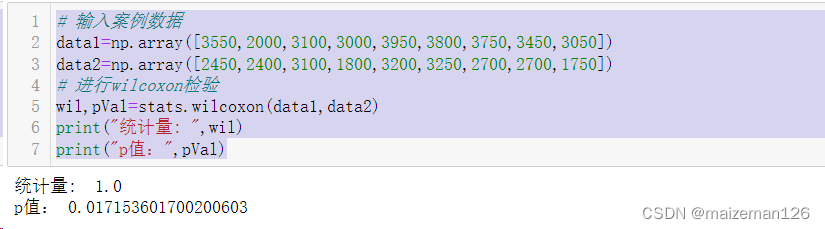
python统计分析——双样本均值比较
参考资料:python统计分析【托马斯】 1、配对样本t检验 在进行两组数据之间的比较时,有两种情况必须区分开。在第一种情况中,同一对象在不同时候的两个记录值进行相互比较。例如,用学生们进入初中时的身高和他们一年后的身高&…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
动态规划-1035.不相交的线-力扣(LeetCode)
一、题目解析 光看题目要求和例图,感觉这题好麻烦,直线不能相交啊,每个数字只属于一条连线啊等等,但我们结合题目所给的信息和例图的内容,这不就是最长公共子序列吗?,我们把最长公共子序列连线起…...
