搜索与图论——Floyd算法求最短路
floyd算法用来求多源汇最短路
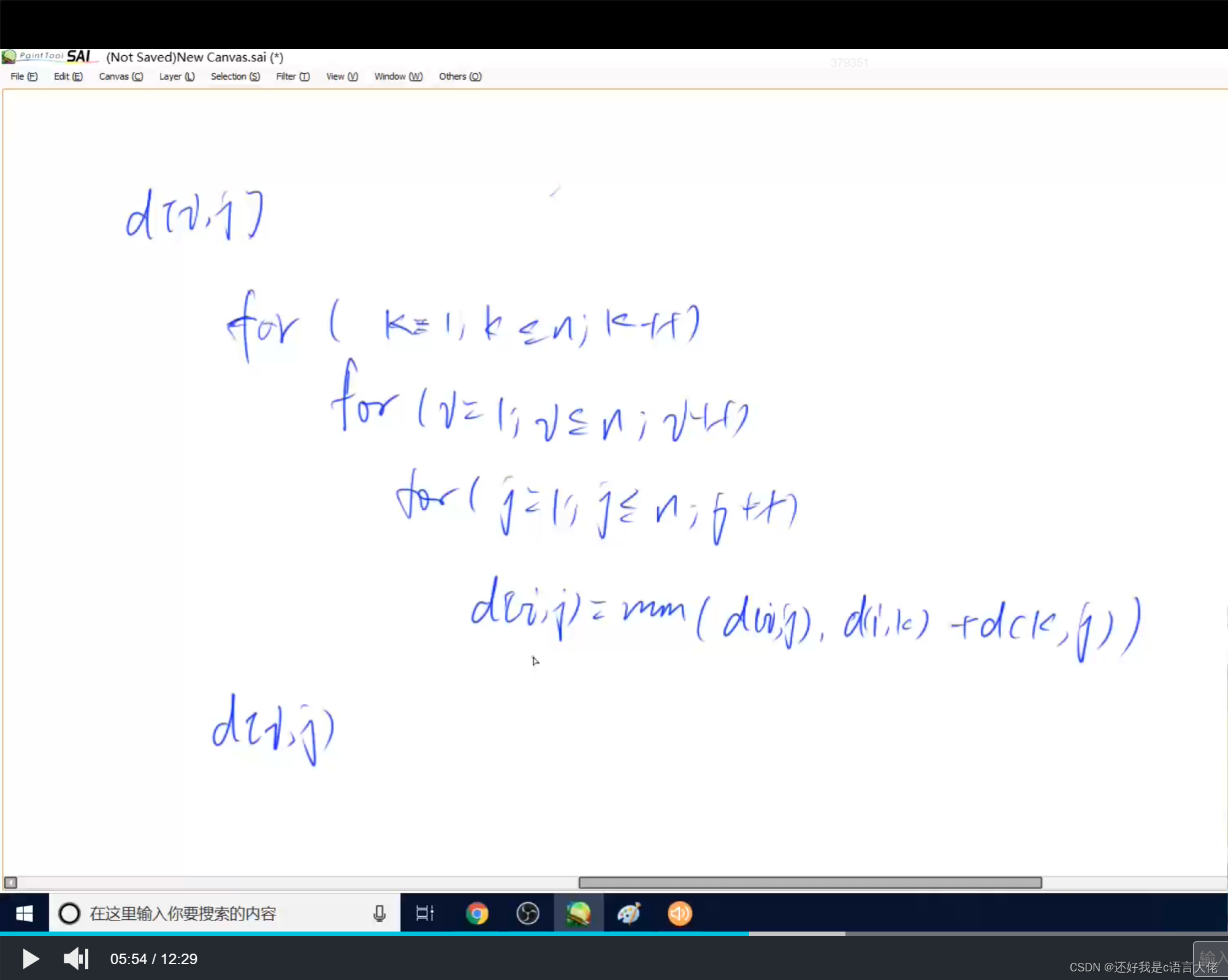
用邻接矩阵来存所有的边
时间复杂度O(n^3)
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N = 20010,INF = 1e9;int n,m,k;
int g[N][N];void floyd(){for(int k = 1;k <= n;k ++ ){for(int i = 1;i <= n;i ++ ){for(int j = 1;j <= n;j ++ ){g[i][j] = min(g[i][j],g[i][k] + g[k][j]);}}}
}int main(){cin >> n >> m >> k;for(int i = 1;i <= n;i ++ ){for(int j = 1;j <= m;j ++ ){if(i == j) g[i][j] = 0;else g[i][j] = INF;}}for(int i = 0;i < m;i ++ ){int x,y,z;cin >> x >> y >> z;g[x][y] = min(g[x][y],z);}floyd();while(k -- ){int x,y;cin >> x >> y;if(g[x][y] > INF / 2) cout << "impossible" << endl; //INF还是要/2,考虑到可能有负权边的情况else cout << g[x][y] <<endl;}return 0;
}相关文章:

搜索与图论——Floyd算法求最短路
floyd算法用来求多源汇最短路 用邻接矩阵来存所有的边 时间复杂度O(n^3) #include<iostream> #include<cstring> #include<algorithm>using namespace std;const int N 20010,INF 1e9;int n,m,k; int g[N][N];void floyd(){for(int k 1;k < n;k ){f…...

春招冲刺百题计划--矩阵篇
289. 生命游戏 题目: 给定一个包含 m n 个格子的面板,每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态: 1 即为 活细胞 (live),或 0 即为 死细胞 (dead)。每个细胞与…...
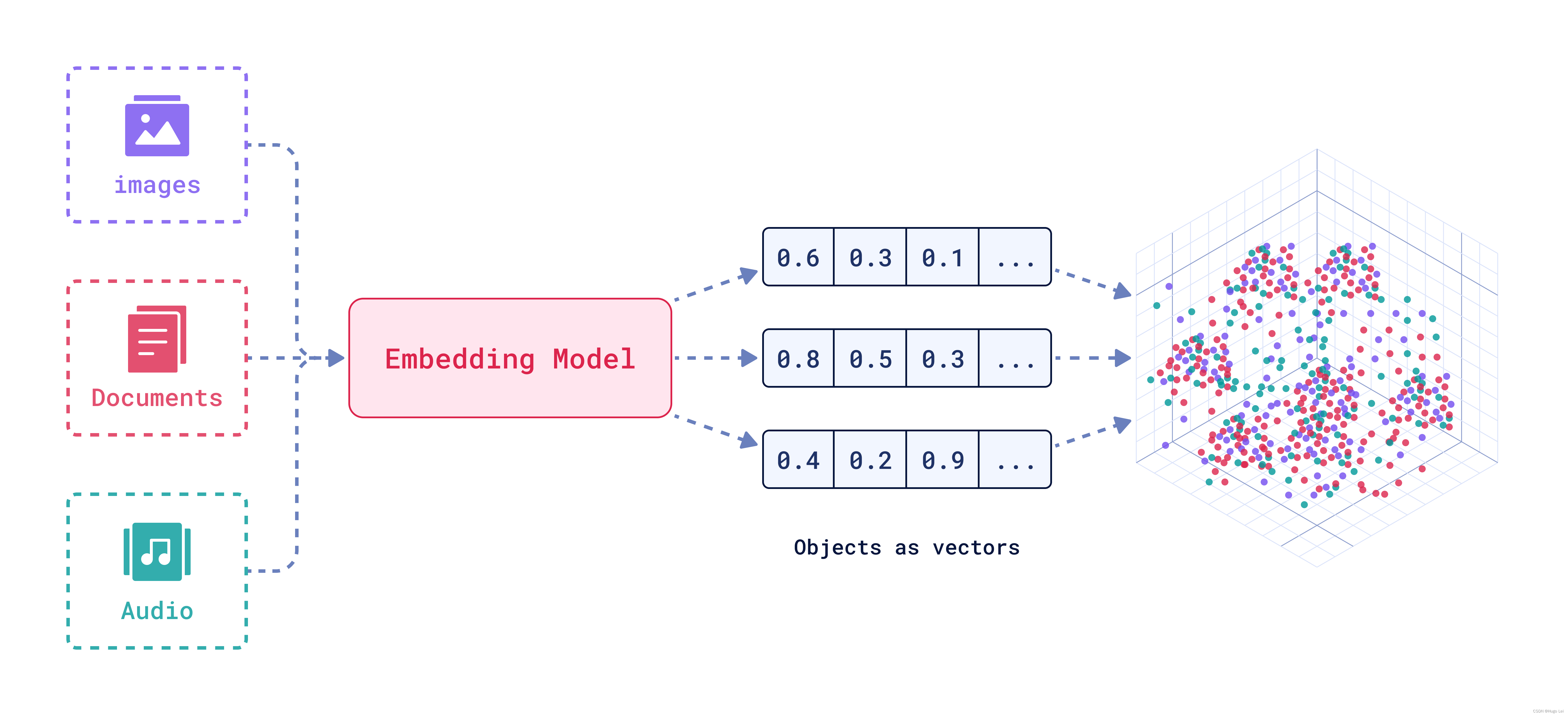
LLM大语言模型(八):ChatGLM3-6B使用的tokenizer模型BAAI/bge-large-zh-v1.5
背景 BGE embedding系列模型是由智源研究院研发的中文版文本表示模型。 可将任意文本映射为低维稠密向量,以用于检索、分类、聚类或语义匹配等任务,并可支持为大模型调用外部知识。 BAAI/BGE embedding系列模型 模型列表 ModelLanguageDescriptionq…...

MySQL中的三种日志
MySQL 包括三种类型的⽇志,分别是 binlog、 redolog 和 undolog,它们分别有不同的作⽤和特点。 binlog (存档日志) binlog(Binary log)是 MySQL 中的⼆进制⽇志⽂件,是 Server 层⽣成的的⽇志…...
(A,B,C,D))
Codeforces Round 932 (Div. 2)(A,B,C,D)
比赛链接 AB都是思维,更确切地说,A考了字符串字典序,很经典的贪心考点,B考了MEX运算。C出的还是比较好的,dp方法值得学习。D题是个不太好想的容斥,主要是变量有点多,容易搞混。 A. Entertainme…...
初识C++ · 入门(2)
目录 1 引用 1.1引用的概念 1.2 引用的特性 2 传值,传引用的效率 3 引用和指针的区别 4 内联函数 4.1 内联函数的定义 4. 2 内联函数的特性 5 关键字auto 5.1关于命名的思考 5.2 关于auto的发展 5.3 auto使用规则 6 范围for的使用 7 空指针 1 引用 …...
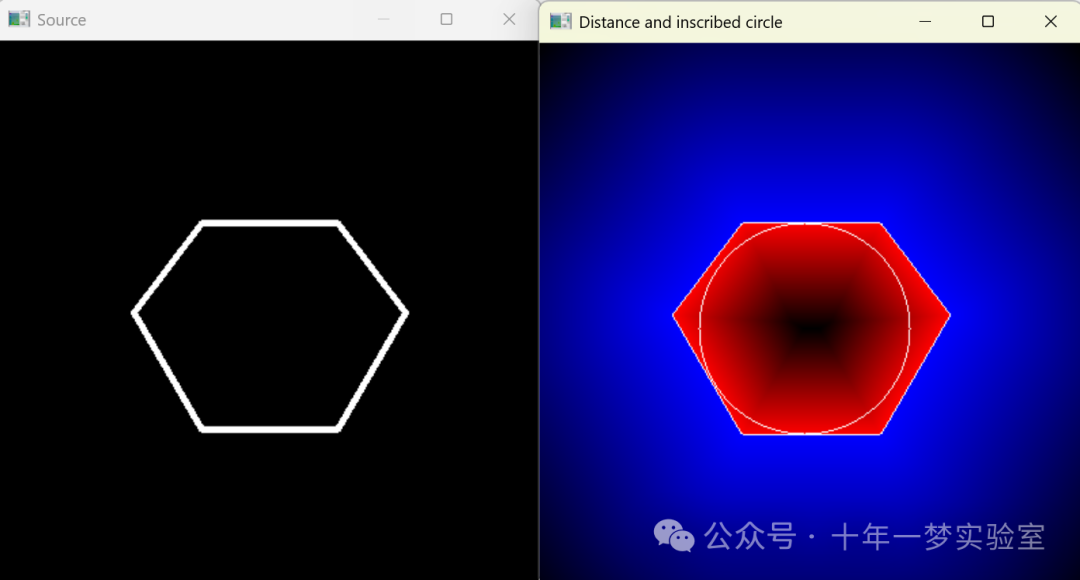
【opencv】教程代码 —ShapeDescriptors
检测和显示图像的轮廓 在图像中搜索并显示轮廓边缘多边形、轮廓矩形和包围圆 获取包含检测到的轮廓的椭圆和旋转的矩形 图像轮廓检测和轮廓凸包 计算图像中的轮廓的矩(包括面积、重心等)并进行显示 创建和绘制一个多边形图像然后计算并显示图像上每个点到…...

2024-03-28 Java8之Collectors类
Collectors类常用方法 文章目录 Collectors类常用方法1.toList、toSet、toMap2.joining、counting、summingInt、minBy3.groupingBy 1.toList、toSet、toMap Collector<T, ?, List<T>> toList(); //收集为List集合 Collector<T, ?, Set<T>> toSet()…...
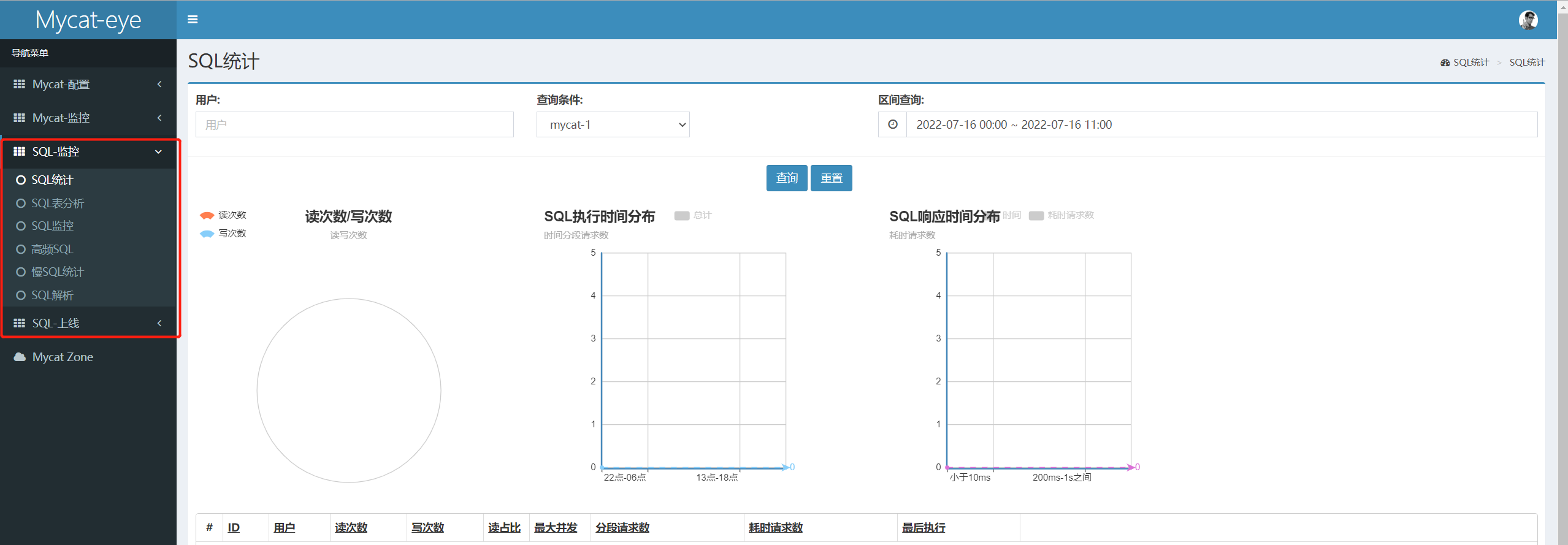
第116讲:使用Mycat-eye管理Mycat数据库服务
文章目录 1.Mycat的管理工具2.Mycat-eye介绍3.部署Mycat-eye3.1.安装Zookeep3.2.安装Mycat-eye3.3.访问Mycat-eye 4.在Mycat-eye中导入Mycat服务的信息 1.Mycat的管理工具 Mycat默认开通2个端口,可以在server.xml中进行修改。 8066 数据访问端口,即进行…...

XR虚拟直播间,引领创新风潮,打破直播局限!
随着互联网技术日新月异的发展,直播行业也迎来了蓬勃发展的春天。然而,大多数直播间在吸引观众眼球和延长用户观看时长方面,仍然面临着巨大的挑战。正是在这样的背景下,XR虚拟直播系统应运而生,以其多维度的直播场景、…...
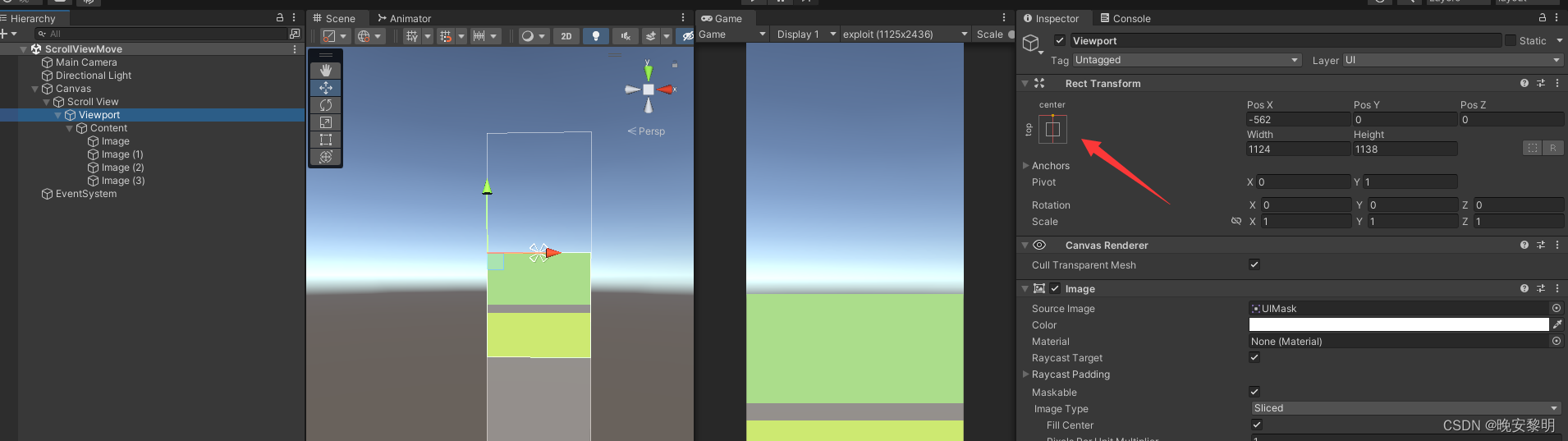
unity双层滑动实现
实现功能: 当滑动列表中内容处于顶端的时候,向上滑动优先滑动整个滑动列表,当滑动列表移动到设置位置,即设定的最高处时,继续移动列表内内容。向下移动亦然,当内容处于滑动列表顶端时,移动整个滑…...

浅谈AI技术创业有哪些机会?
一、AI技术创业概念简介 AI技术创业指的是利用人工智能(Artificial Intelligence,AI)技术进行创业活动。人工智能是指计算机系统能够模拟和展现出人类智能的一种技术。在AI技术创业中,创业者利用AI技术来解决现实生活中的问题&…...
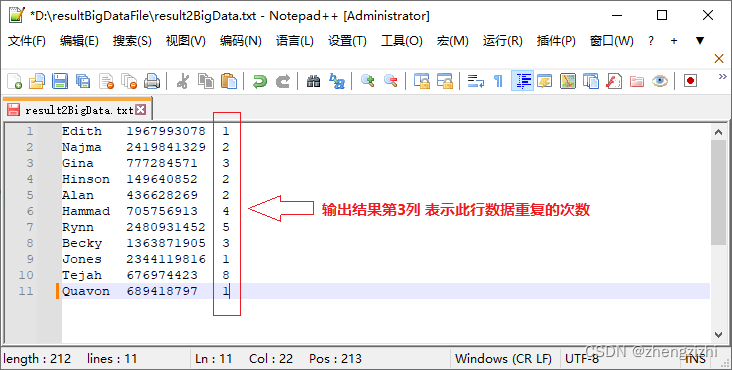
大数据-TXT文本重复行计数工具
支持系统类型:Windows 64位系统 Linux 64位系统 苹果64位系统 硬盘要求:固态硬盘(有效剩余磁盘空间大小最低3倍于大数据文件的大小) 内存要求:最低8G(例如只有几百G数据) 如果处理TB级大数据文…...

【无标题】331
2024年3月31日19:26:09 和一个好感度为40的女生完成了一次基础的对话 2024年3月31日19:26:26 在群里完成了一个毫无所谓的对话 2024年3月31日19:40:04开始准备写论文了 2024年3月31日19:40:11好感度为40的女生回复了我本质上是回复率只有40的人回复了我那应该感到高兴才对 …...
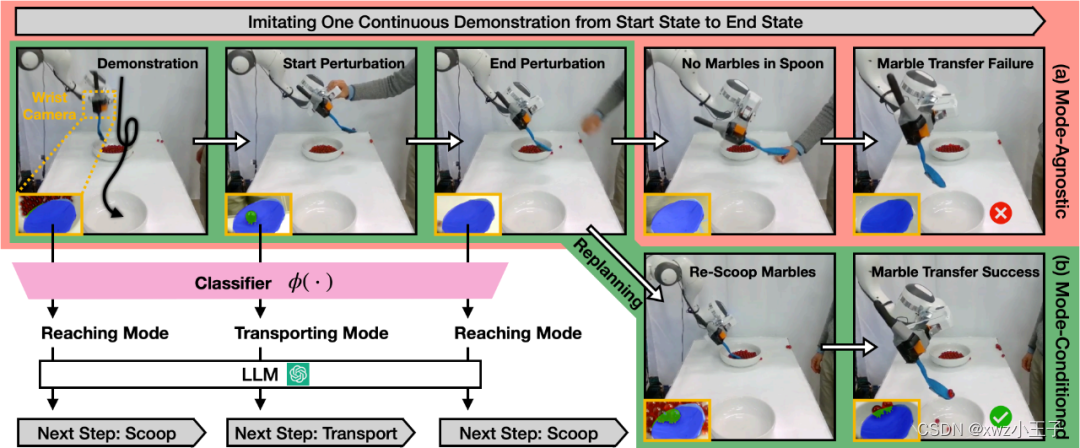
MIT最新研究成果 机器人能够从错误中纠偏 无需编程介入和重复演示
目前科学家们正在努力让机器人变得更加智能,教会他们完成诸如擦拭桌面,端盘子等复杂技能。以往机器人要在非结构化环境执行这样的任务,需要依靠固定编程进行,缺乏场景通用性,而现在机器人的学习过程主要在于模仿&#…...

C语言—指针数组
从键盘任意输入一个整型表示的月份值,用指针数组编程输出该月份的英文表示,若输入的月份值不在1~12之间,则输出“Illegal month”。 **输入格式要求:"%d" 提示信息:"Input month number:&q…...

OpenCV图像二值化
1.二值图像 灰度图像 0 - 255二值图像 0(黑) / 255(白) 2.二值分割 五种阈值分割方法(阈值T): 大于T为255,小于T为0 大于T为0,小于T为255 小于T为原值 else T 小于…...

java中的抽象类
抽象类是指包含了抽象方法的类。在java中,抽象方法指的是用abstract关键字进行修饰的方法,抽象方法与普通的方法的最大区别就是抽象方法没有方法体,也就是说抽象方法是没有具体的实现的。这也就意味着在抽象类的子类中调用抽象方法时…...

代码随想录算法训练营第二十天| 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
系列文章目录 目录 系列文章目录654.最大二叉树递归法[左闭右开)[左闭右闭] 617.合并二叉树递归法(前中后序都可,以前序为例)迭代法(类似 101. 对称二叉树 写法,可用双端队列/单端队列<栈>,以单端队列…...

2014年认证杯SPSSPRO杯数学建模A题(第二阶段)轮胎的花纹全过程文档及程序
2014年认证杯SPSSPRO杯数学建模 A题 轮胎的花纹 原题再现: 轮胎被广泛使用在多种陆地交通工具上。根据性能的需要,轮胎表面常会加工出不同形状的花纹。在设计轮胎时,往往要针对其使用环境,设计出相应的花纹形状。 第二阶段问…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...

基于Python的气象数据分析及可视化研究
目录 一.🦁前言二.🦁开源代码与组件使用情况说明三.🦁核心功能1. ✅算法设计2. ✅PyEcharts库3. ✅Flask框架4. ✅爬虫5. ✅部署项目 四.🦁演示效果1. 管理员模块1.1 用户管理 2. 用户模块2.1 登录系统2.2 查看实时数据2.3 查看天…...
