插入排序、归并排序、堆排序和快速排序的稳定性分析
插入排序、归并排序、堆排序和快速排序的稳定性分析
- 一、插入排序的稳定性
- 二、归并排序的稳定性
- 三、堆排序的稳定性
- 四、快速排序的稳定性
- 总结
在计算机科学中,排序是将一组数据按照特定顺序进行排列的过程。排序算法的效率和稳定性是评价其优劣的两个重要指标。稳定性指的是在排序过程中,相等的元素在排序后保持原有的相对顺序。本文将详细分析插入排序、归并排序、堆排序和快速排序这四种常见排序算法的稳定性,并通过浅显易懂的语言进行解释。

一、插入排序的稳定性
插入排序是一种简单直观的排序算法,它的工作原理类似于我们整理扑克牌的过程。在插入排序中,我们将待排序的元素逐个插入到已排序的序列中,从而得到一个新的有序序列。由于插入排序在每次插入元素时,都会保证已排序序列的有序性,因此它是稳定的排序算法。
具体来说,插入排序从第一个元素开始,认为该元素已经被排序;取出下一个元素,在已经排序的元素序列中从后向前扫描;如果该元素(已排序)大于新元素,将该元素移到下一位置;重复步骤,直到找到已排序的元素小于或者等于新元素的位置;将新元素插入到该位置后。在插入过程中,如果遇到相等的元素,插入排序会将新元素插入到相等元素的后面,从而保证了稳定性。
伪代码示例:
for i from 1 to n-1 do key = A[i] j = i - 1 while j >= 0 and A[j] > key do A[j+1] = A[j] j = j - 1 end while A[j+1] = key
end for
C代码示例:
void insertionSort(int A[], int n) { int i, j, key; for (i = 1; i < n; i++) { key = A[i]; j = i - 1; while (j >= 0 && A[j] > key) { A[j + 1] = A[j]; j = j - 1; } A[j + 1] = key; }
}
二、归并排序的稳定性
归并排序是一种采用分治思想的排序算法。它将待排序序列划分为若干个子序列,每个子序列是有序的;然后再将这些有序子序列逐步合并,最终得到一个完全有序的序列。归并排序在合并过程中,如果遇到相等的元素,会将它们按照原有的相对顺序进行合并,因此归并排序是稳定的排序算法。
具体来说,归并排序首先将待排序序列划分为若干个子序列,每个子序列只包含一个元素,因此它们都是有序的。然后,通过两两合并这些有序子序列,得到更长的有序序列。在合并过程中,如果遇到相等的元素,归并排序会将它们按照原有的相对顺序进行合并。这样,在最终得到的有序序列中,相等元素的相对顺序与原始序列中的相对顺序保持一致,从而保证了稳定性。
伪代码示例:
function mergeSort(A, low, high) if low < high then mid = (low + high) / 2 mergeSort(A, low, mid) mergeSort(A, mid+1, high) merge(A, low, mid, high) end if
end function function merge(A, low, mid, high) n1 = mid - low + 1 n2 = high - mid create arrays Left[n1] and Right[n2] for i from 0 to n1 do Left[i] = A[low + i] end for for j from 0 to n2 do Right[j] = A[mid + 1 + j] end for i = 0 j = 0 k = low while i < n1 and j < n2 do if Left[i] <= Right[j] then A[k] = Left[i] i = i + 1 else A[k] = Right[j] j = j + 1 end if k = k + 1 end while while i < n1 do A[k] = Left[i] i = i + 1 k = k + 1 end while while j < n2 do A[k] = Right[j] j = j + 1 k = k + 1 end while
end function
C代码示例:
void merge(int A[], int low, int mid, int high) { int i, j, k; int n1 = mid - low + 1; int n2 = high - mid; int Left[n1], Right[n2]; for (i = 0; i < n1; i++) Left[i] = A[low + i]; for (j = 0; j < n2; j++) Right[j] = A[mid + 1 + j]; i = 0; j = 0; k = low; while (i < n1 && j < n2) { if (Left[i] <= Right[j]) { A[k] = Left[i]; i++; } else { A[k] = Right[j]; j++; } k++; } while (i < n1) { A[k] = Left[i]; i++; k++; } while (j < n2) { A[k] = Right[j]; j++; k++; }
} void mergeSort(int A[], int low, int high) { if (low < high) { int mid = low + (high - low) / 2; mergeSort(A, low, mid); mergeSort(A, mid + 1, high); merge(A, low, mid, high); }
}
三、堆排序的稳定性
堆排序是一种基于堆数据结构的排序算法。堆是一种特殊的树形数据结构,每个节点都有一个值,且整棵树满足堆的性质:即父节点的值大于或等于(或小于或等于)其子节点的值。堆排序通过构建最大堆或最小堆,然后交换堆顶元素与末尾元素并调整堆的结构,最终得到一个有序序列。然而,堆排序在调整堆的过程中可能会改变相等元素之间的相对顺序,因此堆排序不是稳定的排序算法。
具体来说,在堆排序过程中,当遇到相等的元素时,由于堆的调整过程可能会改变它们之间的相对顺序,因此无法保证排序后的序列中相等元素的相对顺序与原始序列中的相对顺序一致。因此,堆排序不是稳定的排序算法。
伪代码示例:
function heapSort(A) n = length(A) buildMaxHeap(A) for i from n-1 downto 1 do swap A[0] and A[i] maxHeapify(A, 0, i-1) end for
end function function buildMaxHeap(A) n = length(A) for i from floor(n/2)-1 downto 0 do maxHeapify(A, i, n-1) end for
end function function maxHeapify(A, i, heapSize) left = 2*i + 1 right = 2*i + 2 largest = i if left < heapSize and A[left] > A[largest] then largest = left end if if right < heapSize and A[right] > A[largest] then largest = right end if if largest != i then swap A[i] and A[largest] maxHeapify(A, largest, heapSize) end if
end function
C代码示例:
void heapify(int A[], int n, int i) { int largest = i; int left = 2 * i + 1; int right = 2 * i + 2; if (left < n && A[left] > A[largest]) largest = left; if (right < n && A[right] > A[largest]) largest = right; if (largest != i) { int swap = A[i]; A[i] = A[largest]; A[largest] = swap; heapify(A, n, largest); }
} void heapSort(int A[], int n) { for (int i = n / 2 - 1; i >= 0; i--) heapify(A, n, i); for (int i = n - 1; i >= 0; i--) { int temp = A[0]; A[0] = A[i]; A[i] = temp; heapify(A, i, 0); }
}
四、快速排序的稳定性
快速排序是一种高效的排序算法,它采用分治的思想进行排序。快速排序通过选择一个基准元素将待排序序列划分为两个子序列,一个子序列中的元素都小于基准元素,另一个子序列中的元素都大于基准元素;然后递归地对这两个子序列进行快速排序,最终得到一个有序序列。然而,快速排序在划分过程中可能会改变相等元素之间的相对顺序,因此快速排序不是稳定的排序算法。
具体来说,在快速排序过程中,当遇到相等的元素时,由于划分过程可能会将它们分到不同的子序列中,从而导致它们之间的相对顺序发生改变。因此,快速排序无法保证排序后的序列中相等元素的相对顺序与原始序列中的相对顺序一致。因此,快速排序不是稳定的排序算法。
伪代码示例:
function quickSort(A, low, high) if low < high then pi = partition(A, low, high) quickSort(A, low, pi-1) quickSort(A, pi+1, high) end if
end function function partition(A, low, high) pivot = A[high] i = low - 1 for j from low to high-1 do if A[j] <= pivot then i = i + 1 swap A[i] and A[j] end if end for swap A[i+1] and A[high]
C代码示例
#include <stdio.h> // 交换数组中的两个元素
void swap(int* a, int* b) { int temp = *a; *a = *b; *b = temp;
} // 分区函数,返回分区后基准元素的位置
int partition(int A[], int low, int high) { int pivot = A[high]; // 选择最右边的元素作为基准 int i = (low - 1); // 指向最小元素的指针 for (int j = low; j <= high - 1; j++) { // 如果当前元素小于或等于基准元素 if (A[j] <= pivot) { i++; // 增加指针 swap(&A[i], &A[j]); // 交换元素 } } swap(&A[i + 1], &A[high]); // 将基准元素放到正确的位置 return (i + 1); // 返回基准元素的位置
} // 快速排序函数
void quickSort(int A[], int low, int high) { if (low < high) { int pi = partition(A, low, high); // 获取基准元素的位置 // 递归地对基准元素左边和右边的子数组进行排序 quickSort(A, low, pi - 1); quickSort(A, pi + 1, high); }
} // 打印数组的函数
void printArray(int A[], int size) { for (int i = 0; i < size; i++) { printf("%d ", A[i]); } printf("\n");
} // 主函数,测试快速排序
int main() { int A[] = {10, 7, 8, 9, 1, 5}; int n = sizeof(A) / sizeof(A[0]); printf("Original array: \n"); printArray(A, n); quickSort(A, 0, n - 1); printf("Sorted array: \n"); printArray(A, n); return 0;
}
这段代码定义了一个快速排序函数quickSort,一个分区函数partition,以及一个用于交换数组中两个元素的辅助函数swap。主函数main中创建了一个待排序的数组,并调用quickSort函数对其进行排序。排序完成后,使用printArray函数打印排序后的数组。
需要注意的是,快速排序在最坏情况下的时间复杂度为O(n^2),这通常发生在输入数组已经排序或接近排序的情况下。为了避免这种情况,可以采取一些策略,如随机选择基准元素或使用三数取中法来选择基准元素。然而,在平均情况下,快速排序的时间复杂度为O(n log n),并且由于其原地排序的特性(不需要额外的存储空间),它在实践中被广泛使用
总结
综上所述,插入排序和归并排序是稳定的排序算法,而堆排序和快速排序不是稳定的排序算法。在实际应用中,我们需要根据具体的需求和数据特征选择合适的排序算法。如果稳定性是首要考虑的因素,那么插入排序和归并排序将是更好的选择;如果对排序速度有较高要求且可以容忍一定程度的不稳定性,那么堆排序和快速排序也是值得考虑的选项。
需要注意的是,虽然本文重点分析了这四种排序算法的稳定性,但在实际应用中还需要考虑其他因素,如算法的时间复杂度、空间复杂度以及数据规模等。只有综合考虑这些因素,才能选择出最适合具体应用场景的排序算法。
此外,对于稳定性的理解也需要注意一些细节。稳定性并不是所有情况下都需要考虑的因素,有些应用场景可能并不关心排序算法是否稳定。因此,在选择排序算法时,我们需要根据具体的应用场景和需求来进行权衡和选择。
最后,需要强调的是,排序算法的选择和使用是一个非常重要的计算机科学问题。在实际应用中,我们需要根据具体的问题和数据特征来选择合适的排序算法,并进行必要的优化和调整。只有这样,才能充分发挥排序算法的优势,提高程序的效率和性能。
相关文章:

插入排序、归并排序、堆排序和快速排序的稳定性分析
插入排序、归并排序、堆排序和快速排序的稳定性分析 一、插入排序的稳定性二、归并排序的稳定性三、堆排序的稳定性四、快速排序的稳定性总结 在计算机科学中,排序是将一组数据按照特定顺序进行排列的过程。排序算法的效率和稳定性是评价其优劣的两个重要指标。稳定…...
【pytest、playwright】多账号同时操作
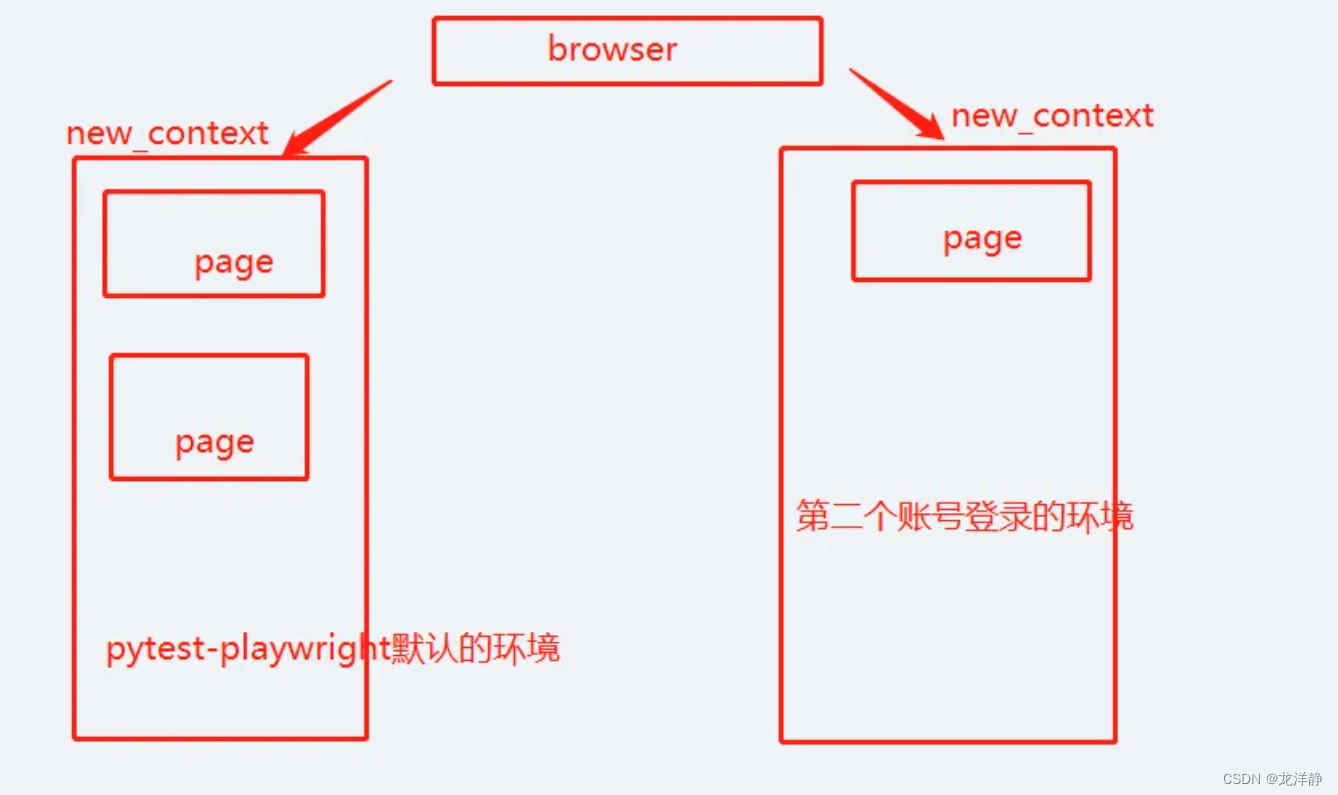
目录 方案实现思路: 方案一: 方案二: 方案实现思路: 依照上图所见,就知道,一个账号是pytest-playwright默认的环境,一个是 账号登录的环境 方案一: 直接上代码: imp…...
软考 系统架构设计师系列知识点之云原生架构设计理论与实践(8)
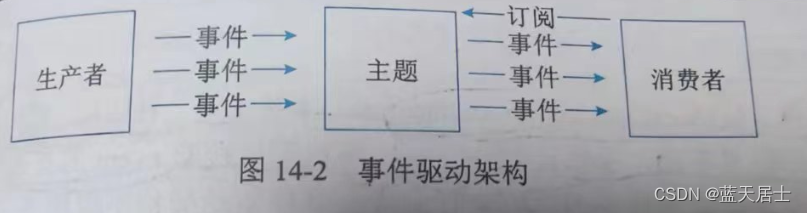
接前一篇文章:软考 系统架构设计师系列知识点之云原生架构设计理论与实践(7) 所属章节: 第14章. 云原生架构设计理论与实践 第2节 云原生架构内涵 14.2 云原生架构内涵 关于云原生的定义有众多版本,对于云原生架构的…...
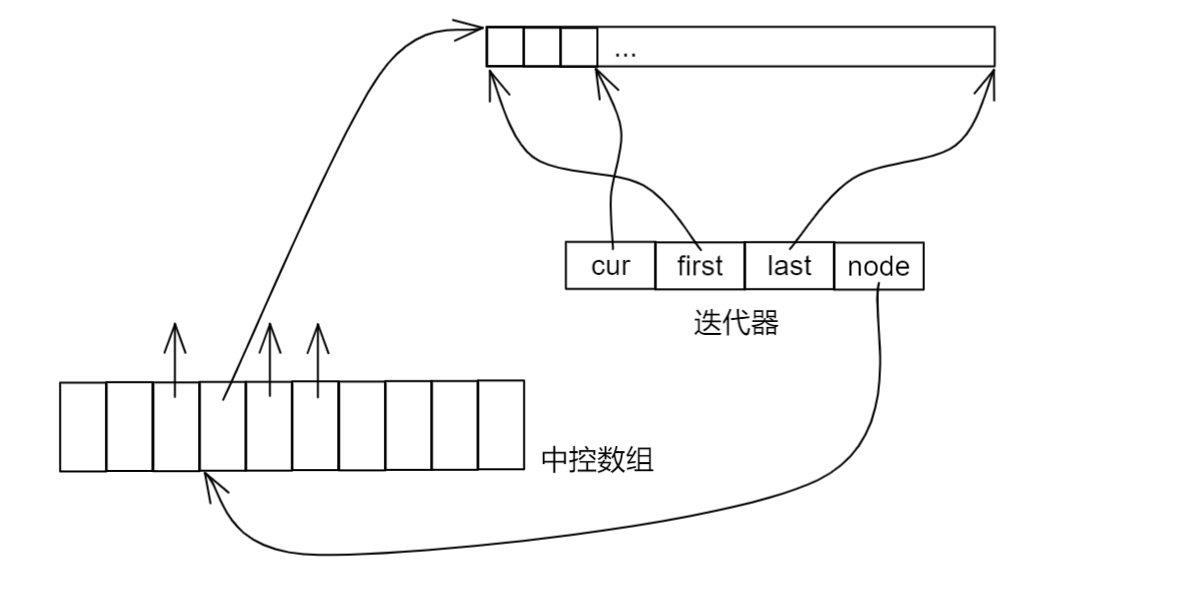
【C++】stack、queue和优先级队列
一、前言 二、stack类 2.1 了解stack 2.2 使用stack (1)empty (2)size (3)top (4)push (5)pop 2.3 stack的模拟实现 三、queue类 3.1 了解queue …...

第十三届蓝桥杯国赛真题 Java C 组【原卷】
文章目录 发现宝藏试题 A: 斐波那契与 7试题 B: 小蓝做实验试题 C: 取模试题 D: 内存空间试题 E \mathrm{E} E : 斐波那契数组试题 F: 最大公约数试题 G: 交通信号试题 I: 打折试题 J: 宝石收集 发现宝藏 前些天发现了一个巨牛的人工智能学习网站,通俗易懂&#x…...

docker部署ubuntu
仓库: https://hub.docker.com/search?qUbuntu 拉一个Ubuntu镜像 docker pull ubuntu:18.04 查看本地镜像: docker images 运行容器 docker run -itd --name ubuntu-18-001 ubuntu:18.04 通过ps命令可以查看正在运行的容器信息 docker ps 进入容器 最…...
iOS问题记录 - App Store审核新政策:隐私清单 SDK签名(持续更新)
文章目录 前言开发环境问题描述问题分析1. 隐私清单 & SDK签名1.1. 隐私清单 - 数据使用声明1.2. 隐私清单 - 所用API原因描述1.3. SDK签名 2. 即将发布的第三方SDK要求 解决方案最后 前言 前段时间用Flutter开发的iOS App提交了新版本,结果刚过两分钟就收到了…...
ES学习日记(二)-------集群设置
上一节写了elasticsearch单节点安装和配置,现在说集群,简单地说就是在多台服务器上搭建单节点,在配置文件里面增加多个ip地址即可,过程同单节点部署,主要说集群配置 注意:不建议在之前单节点es上修改配置为集群,据说运行之后会生成很多文件,在单点基础上修改容易出现未知问题,…...

农村集中式生活污水分质处理及循环利用技术指南
立项单位:生态环境部土壤与农业农村生态环境监管技术中心、山东文远环保科技股份有限公司、北京易境创联环保有限公司、中国环境科学研究院、广东省环境科学研究院、中铁第五勘察设计院集团有限公司、中华环保联合会水环境治理专业委员会 本文件规定了集中式村镇生活…...
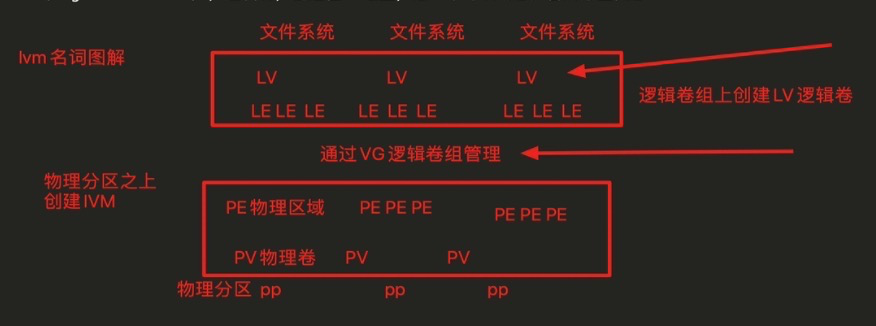
linux 一些命令
文章目录 linux 一些命令fdisk 磁盘分区parted 分区文件系统mkfs 格式化文件系统fsck 修复文件系统 mount 挂载swap 交换分区清除linux缓存df du 命令raid 命令基本原理硬raid 和 软raid案例raid 10 故障修复,重启与卸载 lvm逻辑卷技术LVM的使用方式LVM 常见名词解析…...
移动硬盘损坏打不开?别急,这里有解决方案!
在日常工作和生活中,移动硬盘几乎成为了我们必不可少的存储设备,它小巧便捷,能够容纳大量的数据。然而,当移动硬盘突然损坏打不开时,那份焦虑与无助几乎无法用言语来形容。那些重要的文件、珍贵的照片,似乎…...

微信小程序【从入门到精通】——服务器的数据交互
👨💻个人主页:开发者-曼亿点 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 曼亿点 原创 👨💻 收录于专栏:…...
Python爬虫-懂车帝城市销量榜单
前言 本文是该专栏的第23篇,后面会持续分享python爬虫干货知识,记得关注。 最近粉丝留言咨询某汽车平台的汽车销量榜单数据,本文笔者以懂车帝平台为例,采集对应的城市汽车销量榜单数据。 具体的详细思路以及代码实现逻辑,跟着笔者直接往下看正文详细内容。(附带完整代码…...

《QDebug 2024年3月》
一、Qt Widgets 问题交流 1. 二、Qt Quick 问题交流 1.Qt5 ApplicationWindow 不能使用父组件 Window 的 transientParent 属性 ApplicationWindow 使用 transientParent 报错: "ApplicationWindow.transientParent" is not available due to compone…...

C# OpenCvSharp-HoughCircles(霍夫圆检测) 简单计数
目录 效果 项目 代码 下载 效果 项目 代码 using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text; using System.Windows.Forms; using OpenCvSharp; using O…...

MybatisPlus速成
MybatisPlus快速入门 快速入门入门案例常见注解常见配置 核心功能条件构造器自定义SQLService接口 扩展功能代码生成静态工具逻辑删除枚举处理器JSON处理器 插件功能分页插件通用分页实体 参考文档 mybatis-plus参考文档 全部资料链接 讲义 快速入门 入门案例 <dependency…...
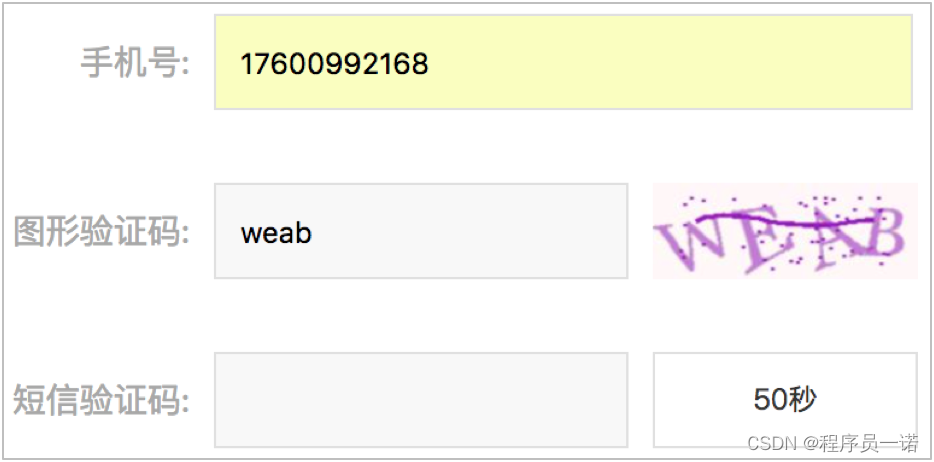
【Django开发】0到1美多商城项目md教程第4篇:图形验证码,1. 图形验证码接口设计【附代码文档】
美多商城完整教程(附代码资料)主要内容讲述:欢迎来到美多商城!,项目准备。展示用户注册页面,创建用户模块子应用。用户注册业务实现,用户注册前端逻辑。图形验证码,图形验证码接口设…...
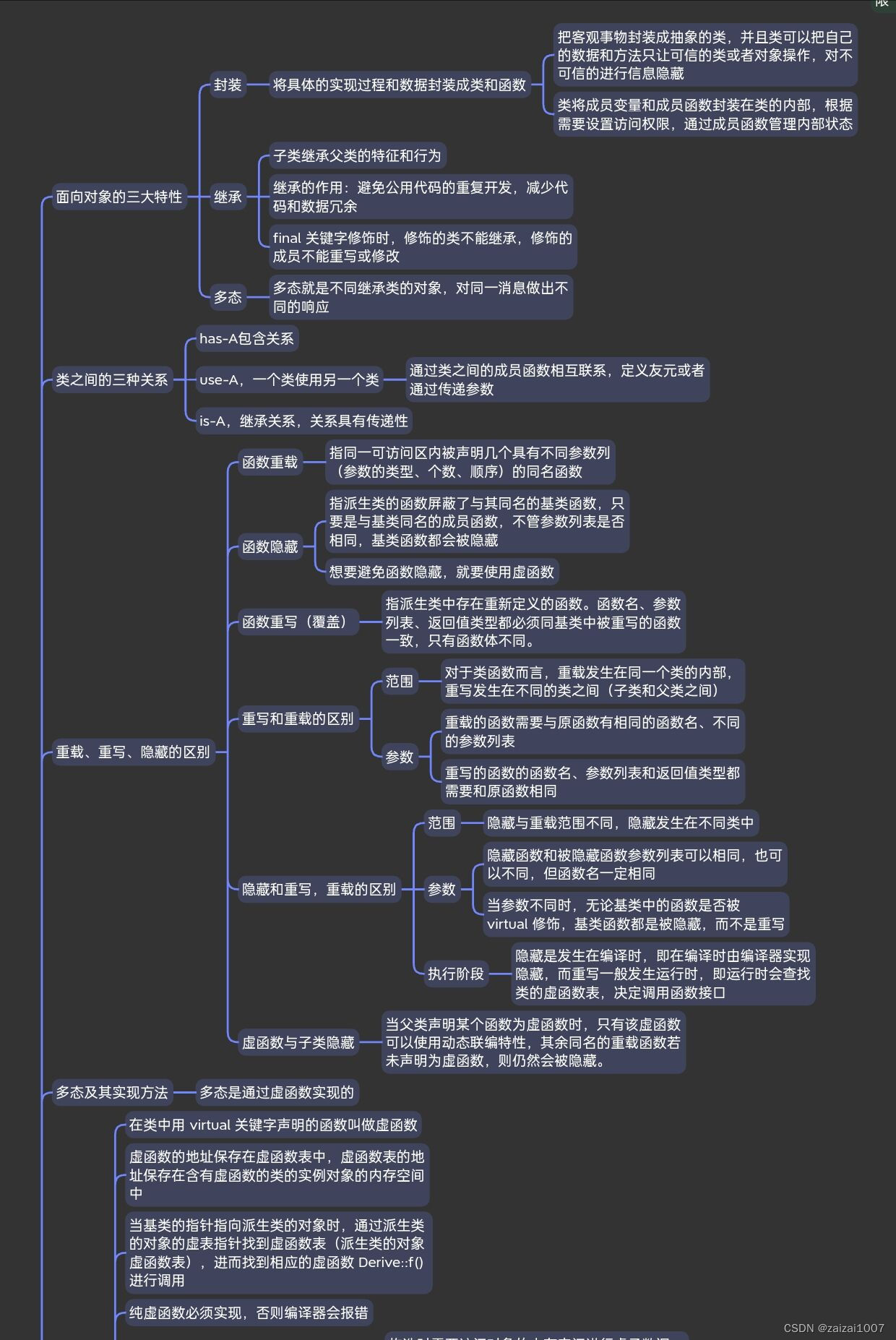
八股 -- C#
面向对象 (三大特性) 三大特性目的是为了提供更好的代码组织、可维护性、扩展性和重用性 C#基础——面向对象 - 知乎 (zhihu.com) 封装 理解: 你不需要了解这个方法里面写了什么代码,你只需要了解这个方法能够给你返回什么数据&…...

科创新格局·共赢双循环“2024上海智能科技与创新展览会”
2024上海智能科技与创新展览会,将于6月中旬在上海新国际博览中心隆重召开。作为一场盛大的科技盛会,此次展览会将汇聚科技前瞻趋势,融合产业贸易优势,布局初创投资赛道,提供全方位场景生态的跨界合作,构建“…...
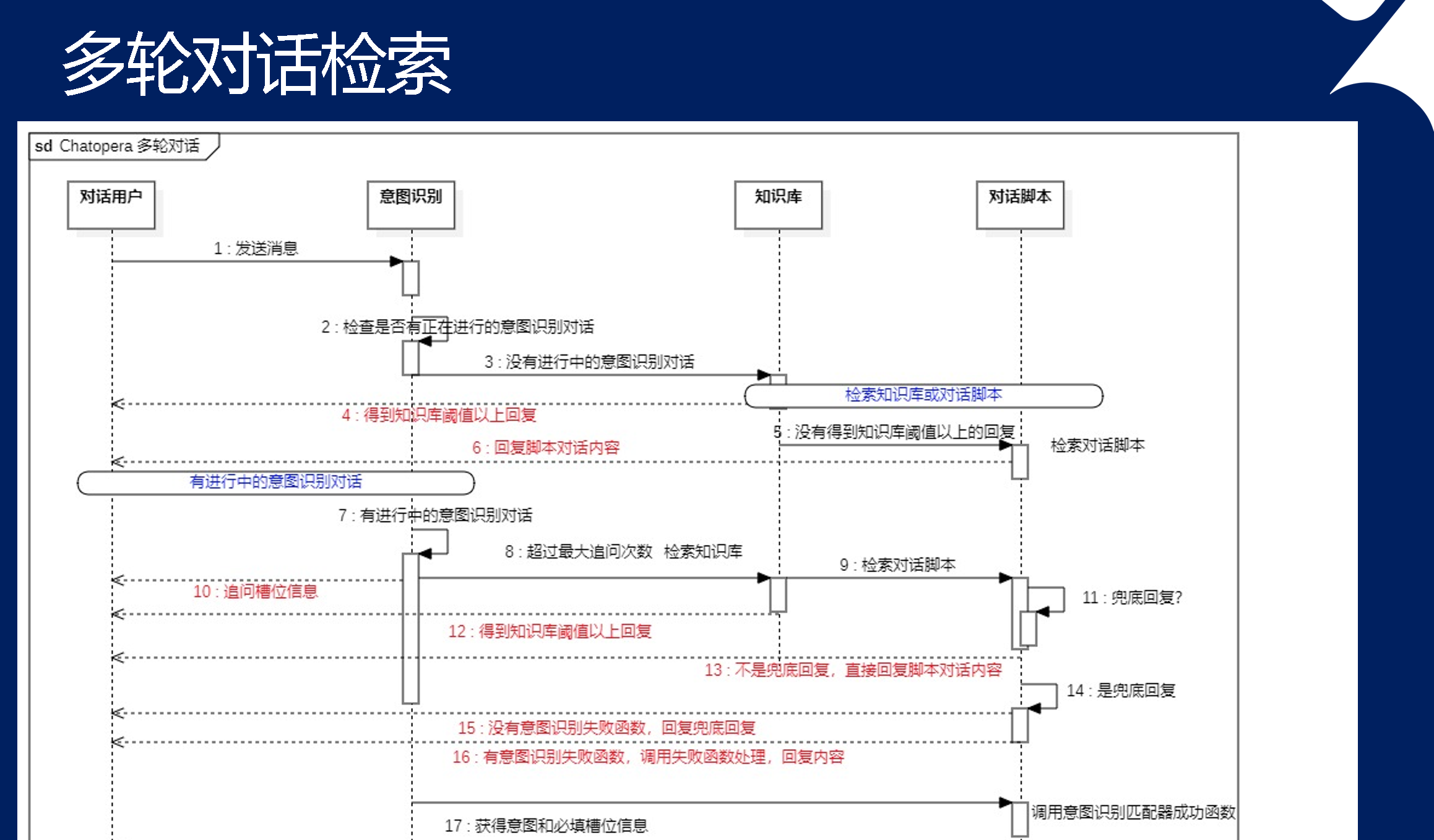
Chatopera 云服务的智能问答引擎实现原理,如何融合 #聊天机器人 技术 #Chatbot #AI #NLP
观看视频 Bilibili: https://www.bilibili.com/video/BV1pZ421q7EH/YouTube: https://www.youtube.com/watch?vx0d1_0HQa8o 内容大纲 提前在浏览器打开网址: Chatopera 云服务:https://bot.chatopera.comChatopera 入门教程:https://dwz…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
