[leetcode] 100. 相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:

输入:p = [1,2,3], q = [1,2,3]
输出:true
示例 2:
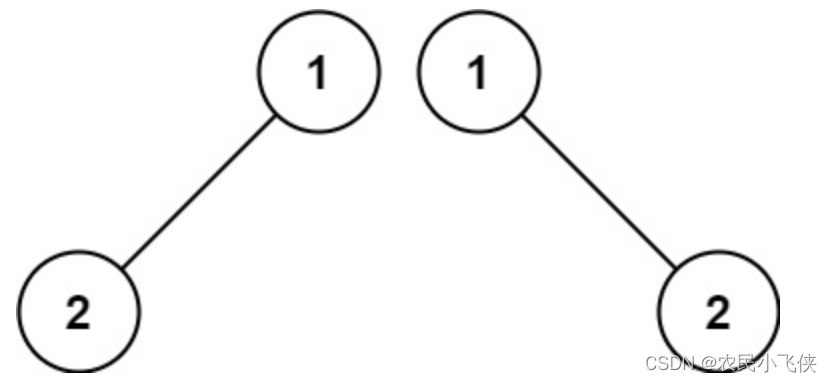
输入:p = [1,2], q = [1,null,2]
输出:false
示例 3:
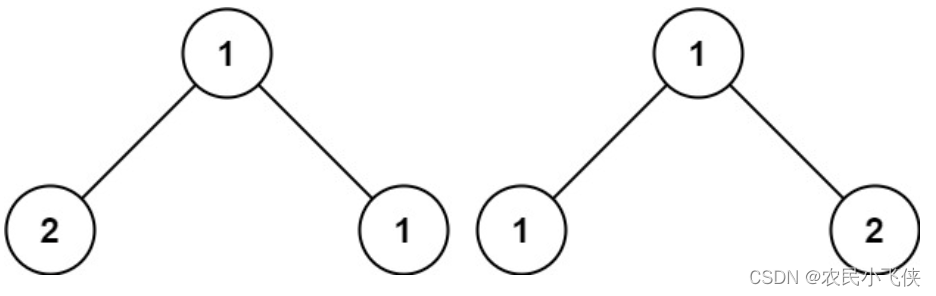
输入:p = [1,2,1], q = [1,1,2]
输出:false
提示:
- 两棵树上的节点数目都在范围 [0, 100] 内
- -104 <= Node.val <= 104
Python实现
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:if not p and not q:return Trueelif not p or not q:return Falseelif p.val!=q.val:return Falseelse:left=self.isSameTree(p.left,q.left)right = self.isSameTree(p.right,q.right)return left and right
相关文章:

[leetcode] 100. 相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。 如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。 示例 1: 输入:p [1,2,3], q [1,2,3] 输出:true示例 2&a…...

08、Lua 函数
Lua 函数 Lua 函数Lua函数主要有两种用途函数定义解析:optional_function_scopefunction_nameargument1, argument2, argument3..., argumentnfunction_bodyresult_params_comma_separated 范例 : 定义一个函数 max()Lua 中函数可以作为参数传递给函数多返回值Lua函…...

【数据分析面试】1. 计算年度收入百分比(SQL)
题目 你需要为公司的营收来源生成一份年度报告。计算截止目前为止,在表格中记录的第一年和最后一年所创造的总收入百分比。将百分比四舍五入到两位小数。 示例: 输入: annual_payments 表 列名类型amountINTEGERcreated_atDATETIMEstatusV…...

数据库SQL语句速查手册
SQL 语句语法AND / ORSELECT column_name(s) FROM table_name WHERE condition AND|OR conditionALTER TABLEALTER TABLE table_name ADD column_name datatypeorALTER TABLE table_name DROP COLUMN column_nameAS (alias)SELECT column_name AS column_alias FROM table_name…...

智慧城市一屏统览,数字孪生综合治理
现代城市作为一个复杂系统,牵一发而动全身,城市化进程中产生新的矛盾和社会问题都会影响整个城市系统的正常运转。智慧城市是应对这些问题的策略之一。城市工作要树立系统思维,从构成城市诸多要素、结构、功能等方面入手,系统推进…...
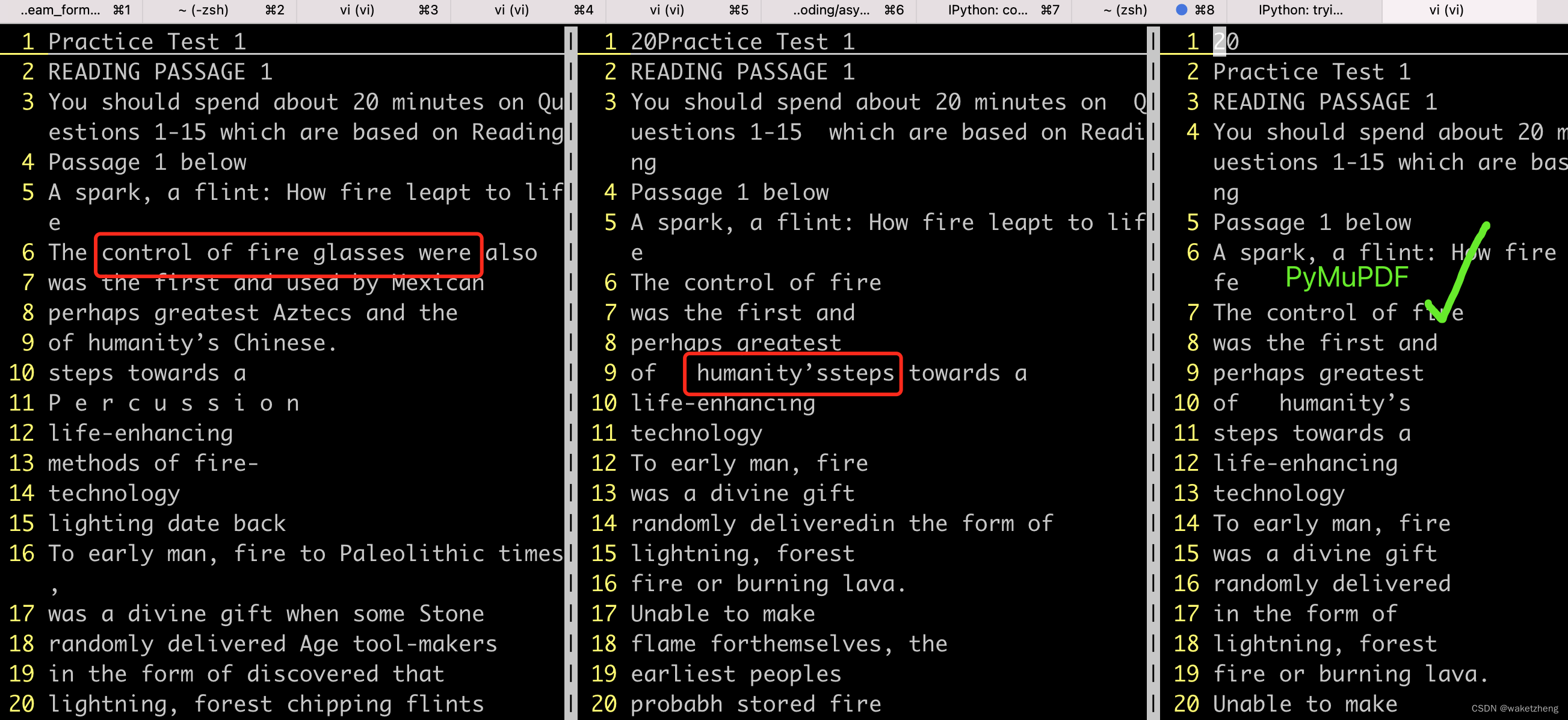
Python读取PDF文字转txt,解决分栏识别问题,能读两栏
搜索了一下,大致有这些库能将PDF转txt 1. PyPDF/PyPDF2(截止2024.03.28这两个已经合并成了一个)pypdf PyPI 2. pdfplumber GitHub - jsvine/pdfplumber: Plumb a PDF for detailed information about each char, rectangle, line, et cete…...
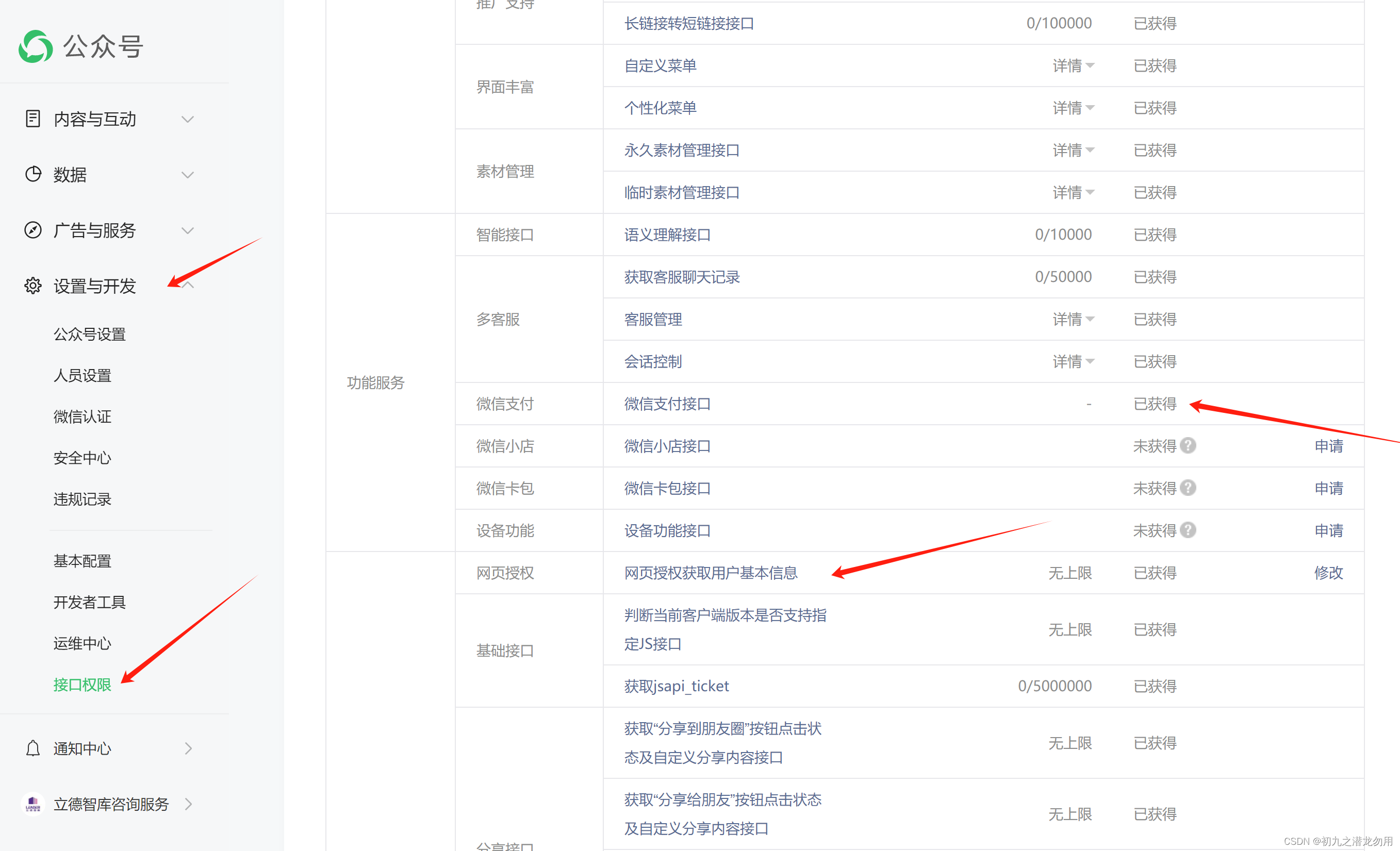
微信支付平台与微信服务号关联配置要点
目录 JSAPI支付 前期资料及相关准备 申请微信服务号 服务号配置要点 微信认证 基本配置 功能设置 申请微信支付号 支付号配置要点 设置操作密码 API安全 开发设置 与服务号关联 小结 JSAPI支付 我们的开发应用场景以JSAPI支付为举例,这也是常用的一…...

C++类复习
C类 1. 类内成员函数隐式声明为inline class Str {int x;int y 3; public:inline void fun(){std::cout<<"pf,yes!"<<std::endl;} };这段代码不会报错,但是类内的成员函数隐式声明为inline函数,不需要单独写在前面。因此将成员…...
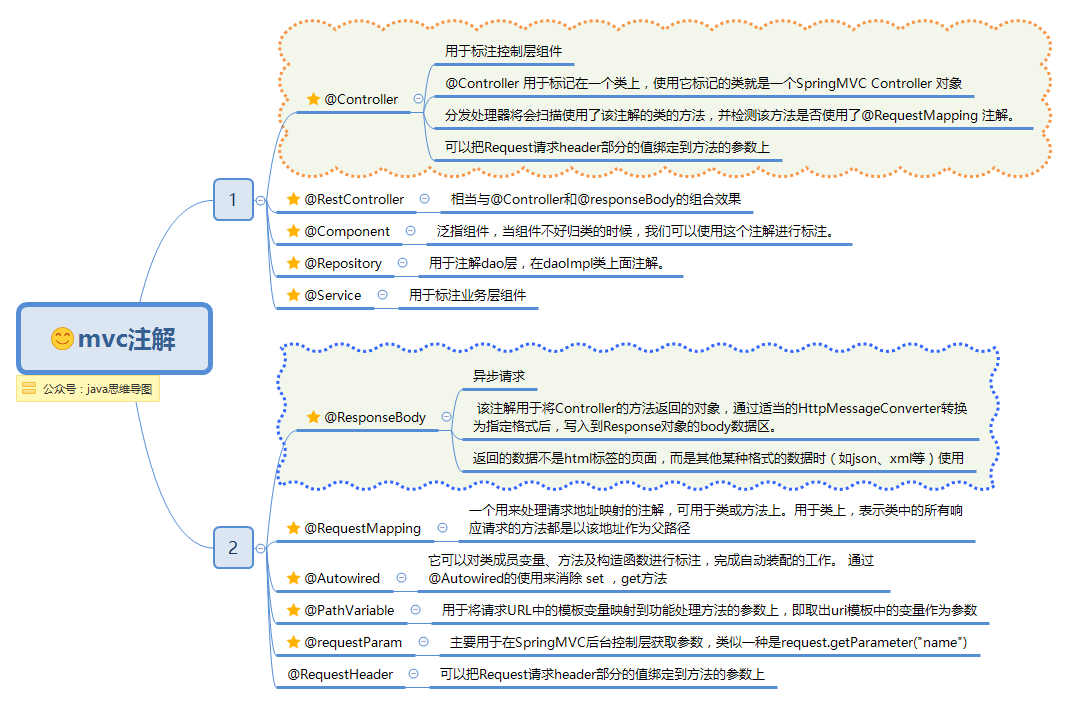
Spring使用(一)注解
Spring使用 资源 Spring 框架内部使用 Resource 接口作为所有资源的抽象和访问接口,在上一篇文章的示例代码中的配置文件是通过ClassPathResource 进行封装的,ClassPathResource 是 Resource 的一个特定类型的实现,代表的是位于 classpath …...
Linux基本指令篇
在前边,我们已经了解过了Linux操作系统的发展和应用,从该篇起,就正式进入对Linux的学习。 今天我们就来在Xshell上远程登录我们的云服务器。首先我们要知道自己云服务器的公网ip,然后修改一下密码。 点击跳转 修改完密码之后我们…...

CSS实现小车旅行动画实现
小车旅行动画实现 效果展示 CSS 知识点 灵活使用 background 属性下的 repeating-linear-gradient 实现路面效果灵活运用 animation 属性与 transform 实现小车和其他元素的动画效果 动画场景分析 从效果图可以看出需要实现此动画的话,需要position属性控制元素…...

6_相机坐标系_相机4个坐标系详述
相机系列文章是用来记录使用opencv3来完成单目相机和6轴机械臂手眼标定。本人吃饭的主职是linux下6轴机械臂相关应用开发。但对于机械臂运动学、相机应用等都非常感兴趣,所以对一些线性代数基础薄弱又想深入了解机械臂内部运算的同志比较有体会。由于是探索性学习&a…...

软考 - 系统架构设计师 - 敏捷开发方法
前言 敏捷开发方法是一种以人为核心、迭代、循序渐进的软件开发方法。它强调团队合作、客户需求和适应变化,旨在通过快速迭代和反馈来快速交付高质量的软件产品。 敏捷开发方法的优势在于能够快速响应变化、提高开发效率和质量、增强团队协作和沟通,并降…...
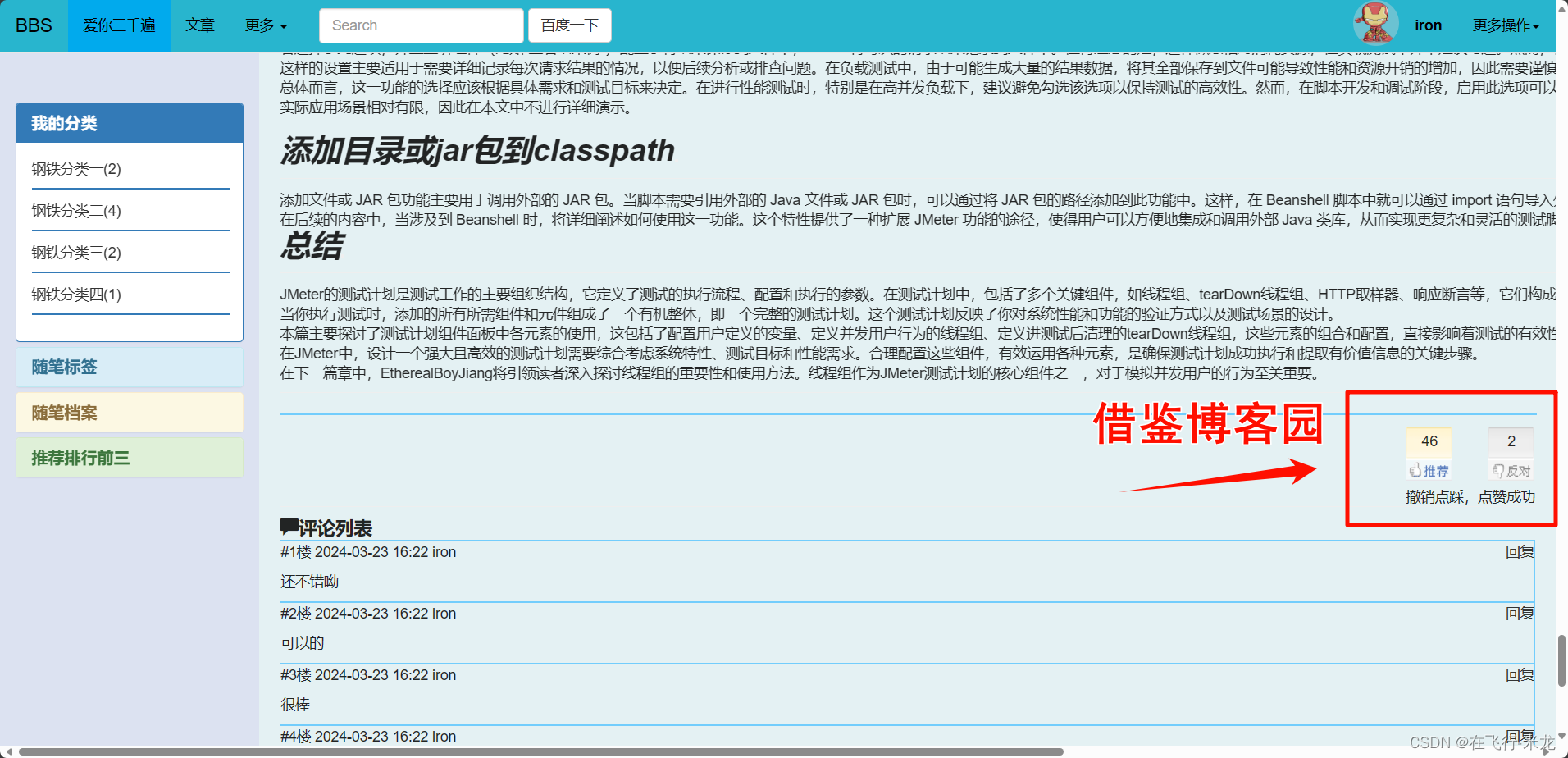
Django 仿博客园练习
数据库搭建 部分功能介绍 【一】注册 (1)效果显示、简单简介 主要亮点 结合了layui和forms组件默认头像可以随着性别的选择发生改变自定义头像可以实时更新显示forms组件报错信息可以局部刷新显示在对应框体下面 没有直接使用layui的前端验证后端验证…...
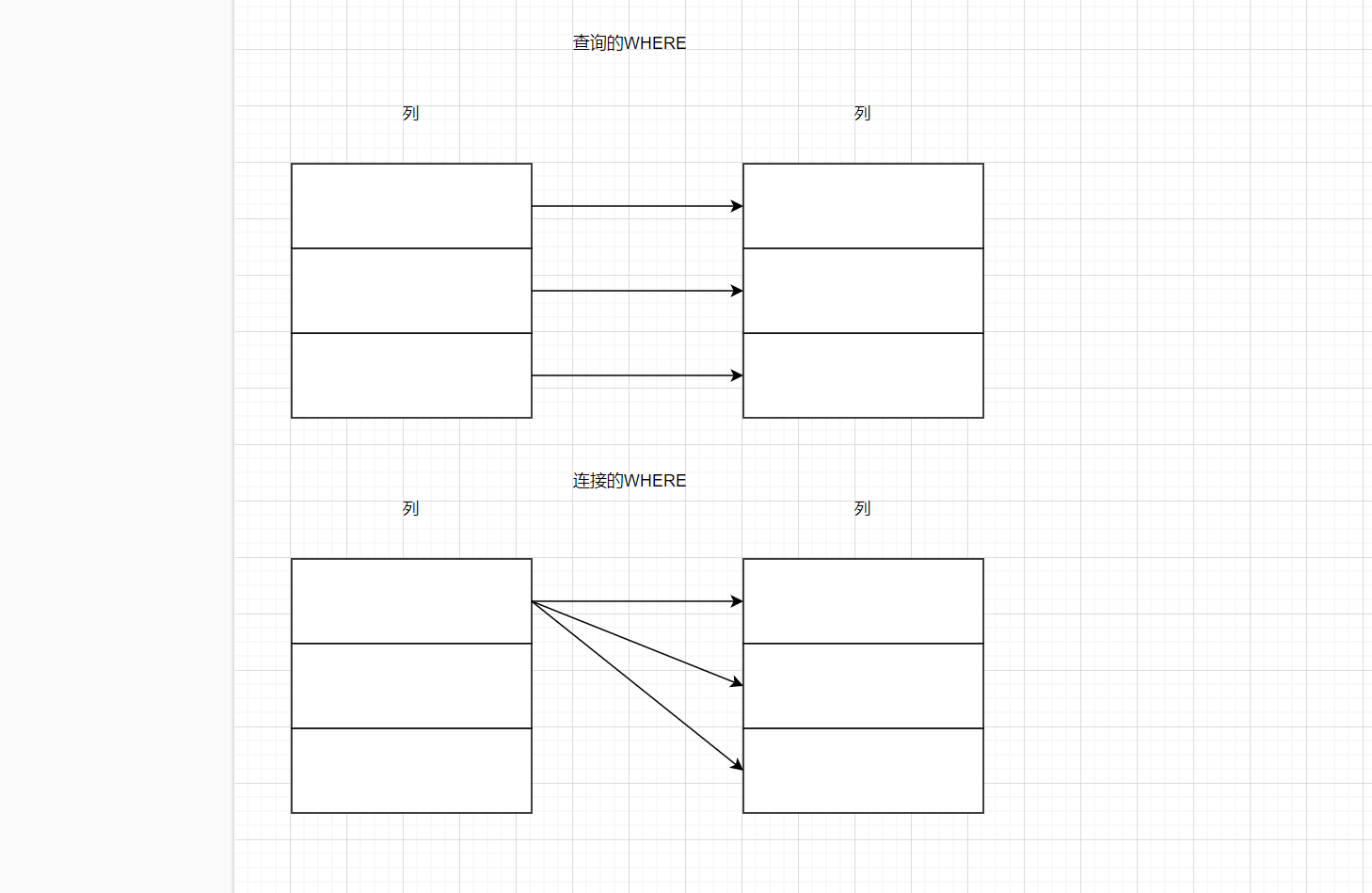
MySQL(常用函数、多表查询)
文章目录 1.数据库函数1.count函数案例答案count(*)与count(列)的区别 2.sum函数案例答案 3.avg函数案例答案 4.max/min函数案例答案 5.group by 分组统计案例答案 6.字符串相关函数演示练习 7.数学相关函数演示 8.日期相关函数演…...
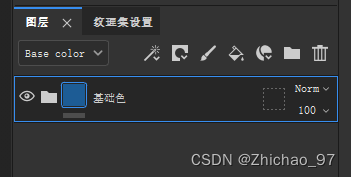
【Pt】马灯贴图绘制过程 01-制作基础色
目录 一、导入模型并烘焙 二、制作基础底漆 (1)底漆层 (2)水痕层 (3)指纹层 一、导入模型并烘焙 1. 导入模型,马灯模型如下所示 2. 在纹理集设置中点击“烘焙模型贴图” 设置输出大小为…...
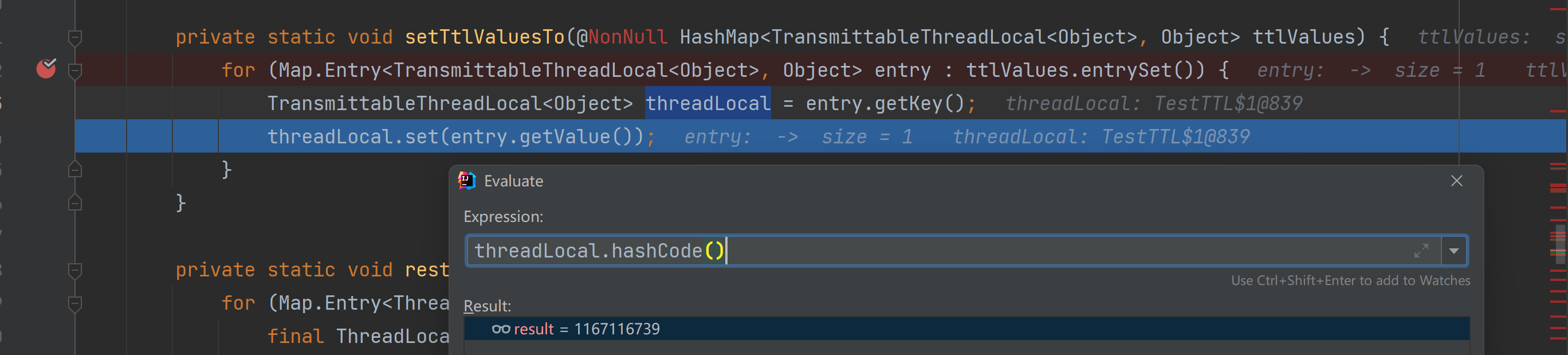
TransmittableThreadLocal 问题杂记
0、前言 TransmittableThreadLocal,简称 TTL,是阿里巴巴开源的一个Java库,它能够实现ThreadLocal在多线程间的值传递,适用于使用线程池、异步调用等需要线程切换的场景,解决了ThreadLocal在使用父子线程、线程池时不能…...
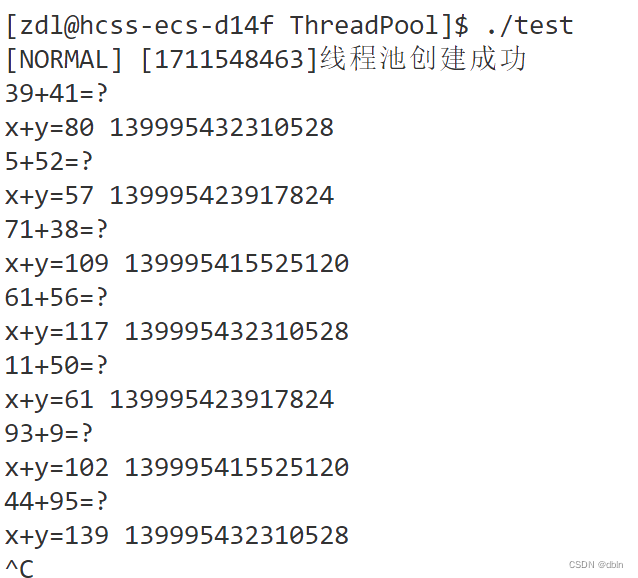
Linux之 线程池 | 单例模式的线程安全问题 | 其他锁
目录 一、线程池 1、线程池 2、线程池代码 3、线程池的应用场景 二、单例模式的线程安全问题 1、线程池的单例模式 2、线程安全问题 三、其他锁 一、线程池 1、线程池 线程池是一种线程使用模式。线程池里面可以维护一些线程。 为什么要有线程池? 因为在…...

Composer常见错误及解决方案
Composer常见错误及解决方案 Composer是PHP的依赖管理工具,它使得在PHP项目中管理和安装依赖库变得简单。然而,在使用Composer时,开发者可能会遇到一些常见的错误。在本文中,我们将探讨一些常见的Composer错误以及相应的解决方案…...
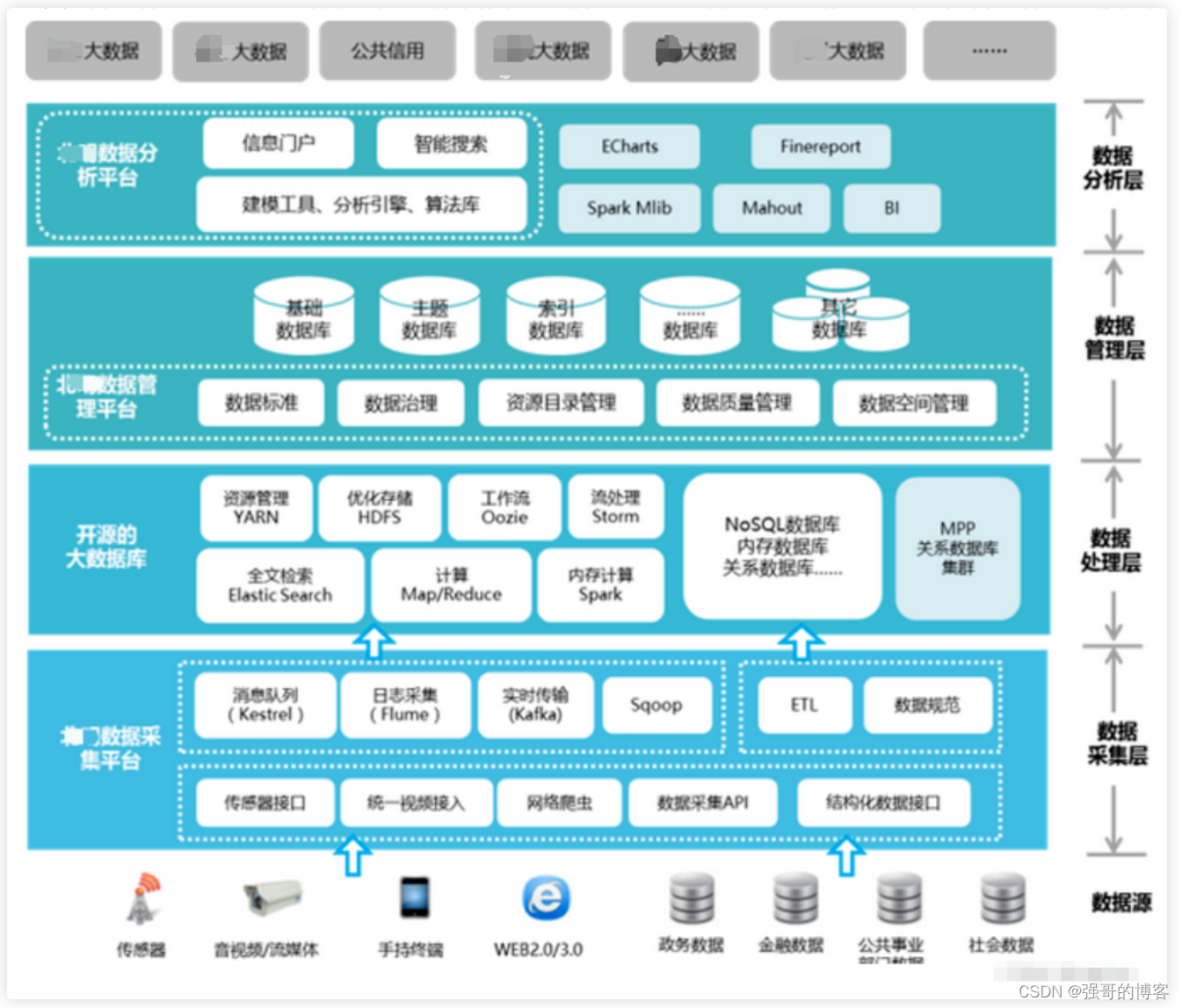
系统架构图怎么画
画架构图是架构师的一门必修功课。 对于架构图是什么这个问题,我们可以按以下等式进行概括: 架构图 架构的表达 架构在不同抽象角度和不同抽象层次的表达,这是一个自然而然的过程。 不是先有图再有业务流程、系统设计和领域模型等&#…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
