算法——图论:判断二分图(染色问题)
题目:. - 力扣(LeetCode)
方法一:并查集
class Solution {
public:vector<int>father;int find(int x){if (father[x] != x)father[x] = find(father[x]);return father[x];}void add(int x1, int x2){int fa1 = find(x1), fa2 = find(x2);if (fa1 != fa2)father[fa1] = fa2;}bool isBipartite(vector<vector<int>>& graph) {father.resize(graph.size());for (int i = 0; i < graph.size(); i++){father[i] = i;}for (int i = 0; i < graph.size(); i++){//if (graph[i].size() == 1 || graph[i].size() == 0)continue;for (int j = 0; j < graph[i].size() ; j++){if(find(i)==find(graph[i][j]))return false;add(graph[i][j], graph[i][0]);}}// int cnt = 0;// for (int i = 0; i < graph.size(); i++)// {// if (find(i) == i )cnt++;// }// return cnt==2;return true;}
};注释的代码为一开始使用的方法,在处理完每个节点之后,从头到尾遍历每一个节点,找出所有祖先的个数。但是本题有可能出现不连通,即单个点。如果这样判断单个点也会算作其中,但是单个点可以属于任何一个集合,所以超过二也是正确的。
后来又尝试改进代码,仍然求出所有的祖先节点数,算上不连通点,最后判断总数是不是偶数。但是还是有问题,比如说有两群点以及一个单个的点,总共三个祖先节点,但是该单个点可以算作其中任何一群,所以是二分图,但是该程序会判断不是二分图。
后来干脆不管不连通点,先使用一个数组遍历标记每个点是不是不连通的,然后在最后求祖先节点的个数时,如果是不连通点则直接跳过。发现还是有问题。具体问题好像忘了?
最后又尝试使用set来判断,仍然不行。最后的最后将整个代码完全使用set,使用两个set,set1和set2,但是代码逻辑上有点问题导致有几个用例无法通过,虽然绝大多数都能通过。
总结出:大道至简。复杂的判断复杂的逻辑绕到最后可能还是错的。真正的解法应该很简单很美妙。如上述代码,判断结束条件为如果当前节点和其邻接点已经是同一个集合的了,则直接返回错误。否则如果到最后都没有发现错误则返回正确。
方法二:深搜
我们任选一个节点开始,将其染成红色,并从该节点开始对整个无向图进行遍历;
在遍历的过程中,如果我们通过节点 u 遍历到了节点 v(即 u 和 v 在图中有一条边直接相连),那么会有两种情况:
如果 v 未被染色,那么我们将其染成与 u 不同的颜色,并对 v 直接相连的节点进行遍历;
如果 v 被染色,并且颜色与 u 相同,那么说明给定的无向图不是二分图。我们可以直接退出遍历并返回 false 作为答案。
当遍历结束时,说明给定的无向图是二分图,返回 true 作为答案。
class Solution {
public:vector<int>color;bool vaild=true;void dfs(vector<vector<int>>& graph,int x,int c){color[x]=c;for(int i=0;i<graph[x].size();i++){if(color[graph[x][i]]==c){vaild=false;return;}else if(color[graph[x][i]]==0)dfs(graph,graph[x][i],c==1?2:1);}}bool isBipartite(vector<vector<int>>& graph) {color.resize(graph.size(),0);for(int i=0;i<graph.size();i++){if(color[i]==0)dfs(graph,i,1);}return vaild;}
};方法三:广搜
思路与深搜类似
class Solution {
private:static constexpr int UNCOLORED = 0;static constexpr int RED = 1;static constexpr int GREEN = 2;vector<int> color;public:bool isBipartite(vector<vector<int>>& graph) {int n = graph.size();vector<int> color(n, UNCOLORED);for (int i = 0; i < n; ++i) {if (color[i] == UNCOLORED) {queue<int> q;q.push(i);color[i] = RED;while (!q.empty()) {int node = q.front();int cNei = (color[node] == RED ? GREEN : RED);q.pop();for (int neighbor: graph[node]) {if (color[neighbor] == UNCOLORED) {q.push(neighbor);color[neighbor] = cNei;}else if (color[neighbor] != cNei) {return false;}}}}}return true;}
};
相关文章:
)
算法——图论:判断二分图(染色问题)
题目:. - 力扣(LeetCode) 方法一:并查集 class Solution { public:vector<int>father;int find(int x){if (father[x] ! x)father[x] find(father[x]);return father[x];}void add(int x1, int x2){int fa1 find(x1), f…...

三步提升IEDA下载速度——修改IDEA中镜像地址
找到IDEA的本地安装地址 D:\tool\IntelliJ IDEA 2022.2.4\plugins\maven\lib\maven3\conf 搜索阿里云maven仓库 复制https://developer.aliyun.com/mvn/guide中红框部分代码 这里也是一样的: <mirror><id>aliyunmaven</id><mirrorOf>*&…...

CentOS7 RPM升级支持BBR TCP/CC的内核版本
列出安装的内核 rpm -qa kernel # yum list installed kernel 删除已安装内核 sudo dnf remove kernel-4.0.4-301.fc22.x86_64 安装内核 rpm --import https://www.elrepo.org/RPM-GPG-KEY-elrepo.org rpm -Uvh http://www.elrepo.org/elrepo-release-7.0-2.el7.elrepo.noar…...

文本向量模型BGE与BGE-M3
BGE模型 BGE模型对应的技术报告为《C-Pack: Packaged Resources To Advance General Chinese Embedding》 训练数据 为了训练BGE向量模型,构建了C-MTP数据集,它包括了用来训练文本向量的文本对数据(问答对、两个同义句子、相同主题的两个文…...
【黑马头条】-day04自媒体文章审核-阿里云接口-敏感词分析DFA-图像识别OCR-异步调用MQ
文章目录 day4学习内容自媒体文章自动审核今日内容 1 自媒体文章自动审核1.1 审核流程1.2 内容安全第三方接口1.3 引入阿里云内容安全接口1.3.1 添加依赖1.3.2 导入aliyun模块1.3.3 注入Bean测试 2 app端文章保存接口2.1 表结构说明2.2 分布式id2.2.1 分布式id-技术选型2.2.2 雪…...
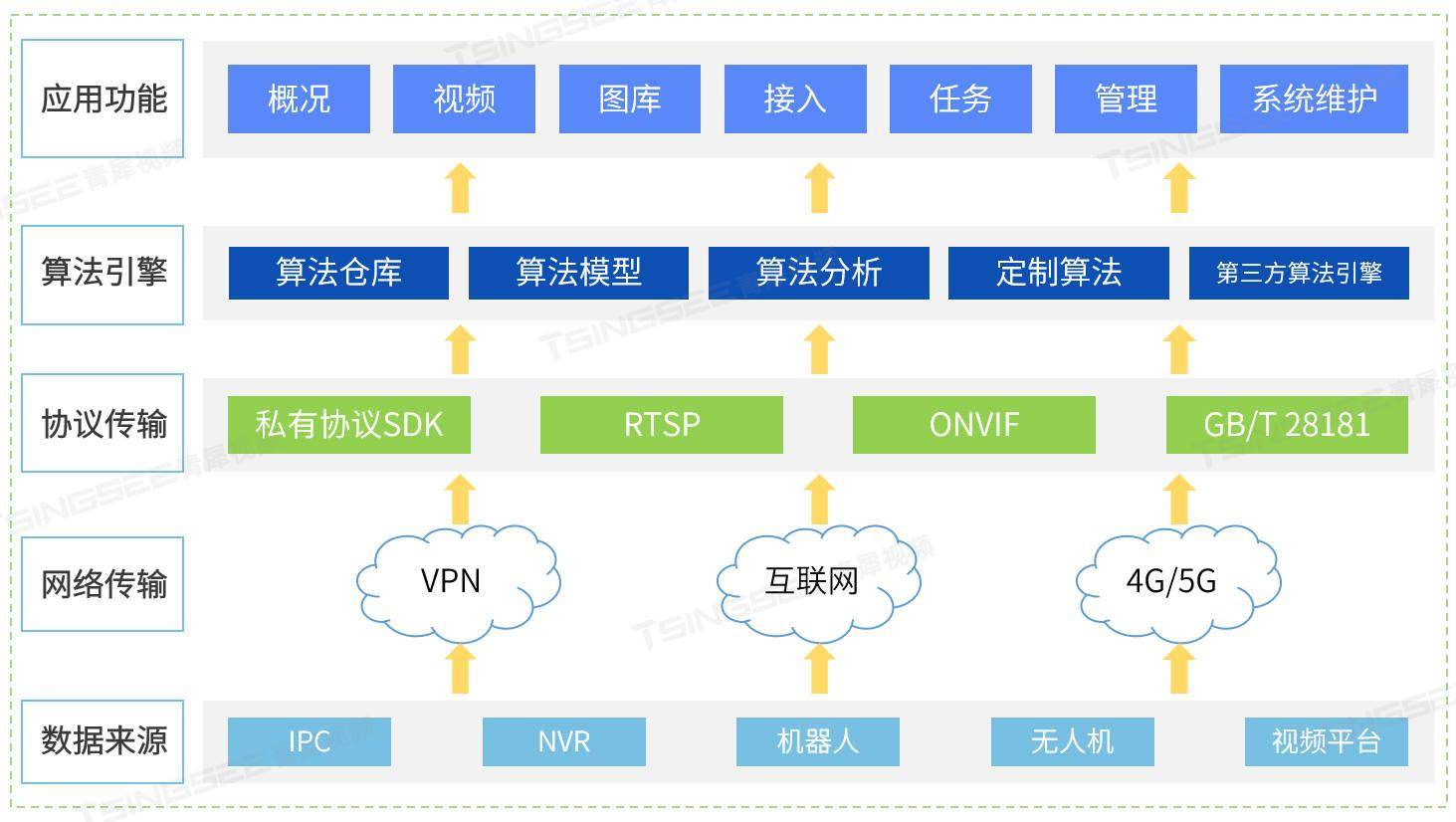
新能源充电桩站场AI视频智能分析烟火检测方案及技术特点分析
新能源汽车充电起火的原因多种多样,涉及技术、设备、操作等多个方面。从技术层面来看,新能源汽车的电池管理系统可能存在缺陷,导致电池在充电过程中出现过热、短路等问题,从而引发火灾。在设备方面,充电桩的设计和生产…...

springboot集成logback-spring.xml文件
彩色日志日志分debug和error文件输出,方便开发人员运维日志限制最大保管天数日志限制总量大小占用量GB日志限制单个文件大小MB日志显示最大保留天数屏蔽没用的日志 <?xml version"1.0" encoding"UTF-8"?> <!--~ Copyright (c) 2020…...

centos7 安装 nginx
一、yum 方式安装 1.安装yum工具 sudo yum install yum-utils 2. 安装epel yum install epel-release 3.安装nginx: yum install nginx 4.查看版本 nginx -v 5.设置开机自启动 systemctl enable nginx nginx 常用命令: 1)启动nginx …...

29. UE5 RPG应用GamplayAbility
前面几篇文章,总算把GE给更新完了,GE的基础应用也算讲清楚了。接下来,我们将更新GA的相应的课程了,首先,这一篇先对GA做一个简单的介绍,然后实现一下如何实现给角色应用一个GA。 简介 GamplayAbility 简称…...

http和https的区别!
HTTP 明文传输,数据都是未加密的,安全性较差,HTTPS(SSLHTTP) 数据传输过程是加密的,安全性较好。 使用 HTTPS 协议需要到 CA(Certificate Authority,数字证书认证机构) …...
使用AOP实现打印日志
首先创建annotation.SystemLog类: package com.gjh.annotation;import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;Target(ElementType.METHOD…...
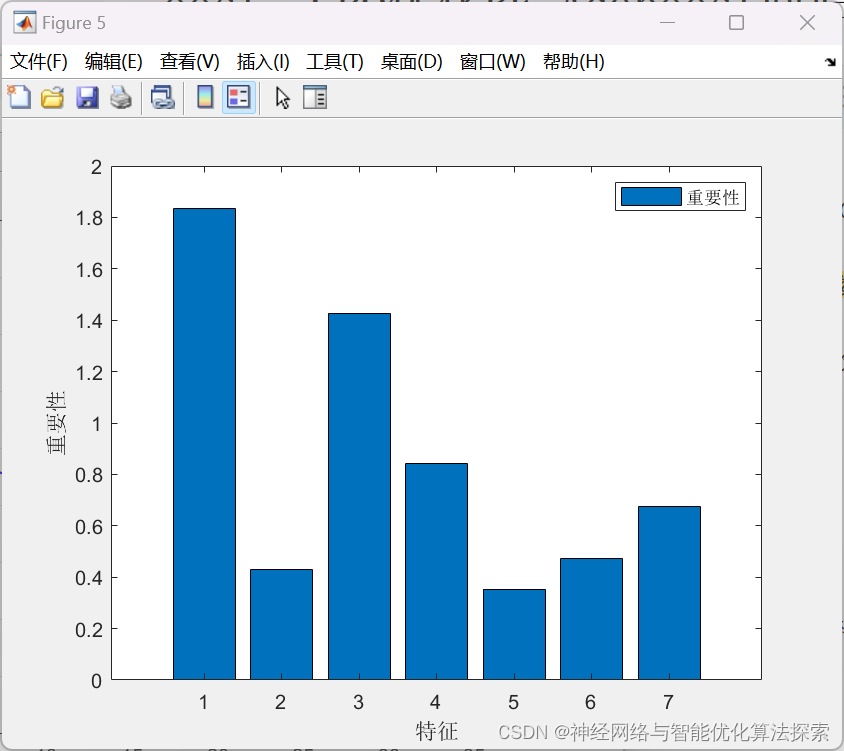
2024年新算法-冠豪猪优化算法(CPO),CPO-RF-Adaboost,CPO优化随机森林RF-Adaboost回归预测-附代码
冠豪猪优化算法(CPO)是一种基于自然界中猪群觅食行为启发的优化算法。该算法模拟了猪群在寻找食物时的集群行为,通过一系列的迭代过程来优化目标函数,以寻找最优解。在这个算法中,猪被分为几个群体,每个群体…...
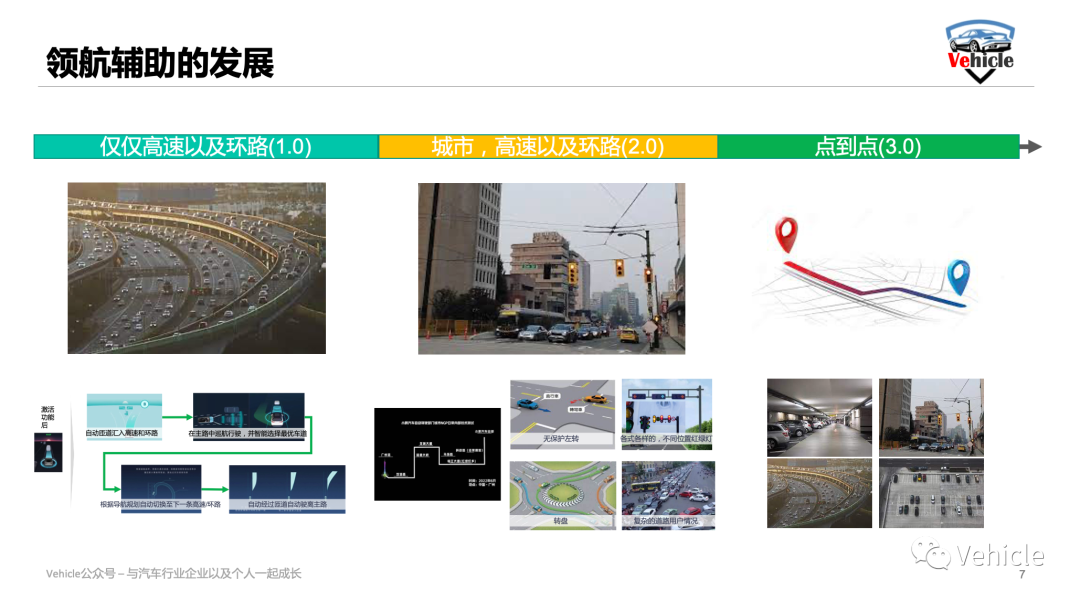
浅谈高阶智能驾驶-NOA领航辅助的技术与发展
浅谈高阶智能驾驶-NOA领航辅助的技术与发展 附赠自动驾驶学习资料和量产经验:链接 2019年在国内首次试驾特斯拉NOA领航辅助驾驶的时候,当时兴奋的觉得未来已来;2020年在试驾蔚来NOP领航辅助驾驶的时候,顿时不敢小看国内新势力了;现在如果哪家…...
大模型 智能体 智能玩具 智能音箱 构建教程 wukong-robot
视频演示 10:27 一、背景 继上文《ChatGPT+小爱音响能擦出什么火花?》可以看出大伙对AI+硬件的结合十分感兴趣,但上文是针对市场智能音响的AI植入,底层是通过轮询拦截,算是hack兼容,虽然官方有提供开发者接口,也免不了有许多局限性(比如得通过特定指令唤醒),不利于我…...

Clickhouse-表引擎探索之MergeTree
引言 前文曾说过,Clickhouse是一个强大的数据库Clickhouse-一个潜力无限的大数据分析数据库系统 其中一个强大的点就在于支持各类表引擎以用于不同的业务场景。 MergeTree MergeTree系列的引擎被设计用于插入极大量的数据到一张表当中。数据可以以数据片段的形式一…...

网络电视盒子哪个好?小编分享电视盒子品牌排行榜
电视盒子使用频率高,功能丰富,价格划算,是我们日常不可或缺的部分,小编经常会被问到与电视盒子相关的问题,考虑到很多朋友并不了解网络电视盒子哪个好,这次我来分享业内权威电视盒子品牌排行榜,…...
)
开源模型应用落地-baichuan2模型小试-入门篇(三)
一、前言 相信您已经学会了如何在Windows环境下以最低成本、无需GPU的情况下运行baichuan2大模型。现在,让我们进一步探索如何在Linux环境下,并且拥有GPU的情况下运行baichuan2大模型,以提升性能和效率。 二、术语 2.1. CentOS CentOS是一种基于Linux的自由开源操作…...

景联文科技高质量大模型训练数据汇总!
3月25日,2024年中国发展高层论坛年会上,国家数据局局长刘烈宏在“释放数据要素价值,助力可持续发展”的演讲中表示,中国10亿参数规模以上的大模型数量已超100个。 当前,国内AI大模型发展仍面临诸多困境。其中ÿ…...

【python】正则表达式
文章目录 正则表达式对象re.RegexObjectre.MatchObject符号说明匹配基础匹配?=、?<=、?!、?<!字符类re模块编译正则表达式compile 函数匹配字符串re.matchre.searchre.findall...

学习vue3第十二节(组件的使用与类型)
1、组件的作用用途 目的: 提高代码的复用度,和便于维护,通过封装将复杂的功能代码拆分为更小的模块,方便管理, 当我们需要实现相同的功能时,我们只需要复用已经封装好的组件,而不需要重新编写相…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
