AtCoder Grand Contest 066 B. Decreasing Digit Sums(构造 打表找规律)
题目
给定一个n(n<=50),记f(x)是x各数位的加和,例如f(331)=3+3+1=7
要求输出一个x(),且对于任意i∈[1,n],均有
成立
思路来源
jiangly B站讲解
题解
首先n没啥用,构造一个n=50成立的case即可,
给定一个x,将x乘以2后,数位和变小,乘以50次都变小
考虑变小怎么做,逆向考虑,
假设终态是10000(若干个0),如果*2=10000变小,
前一项就是5000,这样不断除以2,2500,1250,...
发现前面若干项是变小的,中间也有变大的
乘以若干个2得到最后的10000,那么原始就是不带2的,也就是5的j次方
构造5的j次方,每个*2的时候,都会变小几次,然后变大一次,整体趋势变小,偶有变大
拼接到一起,就能抵消这个偶有变大的情况,只要整体趋势是变小多,变大少
打表发现拼接5的1次方到5的100次方即可,总长度也没有超限
也可以中间补0让各段独立,不过删掉0发现也没有违反性质
Bonus
考虑变大怎么做,
手玩发现,9的时候,会变大,如9,18,36,72,144,288,
144->288会变大,具体打表可以后面虽然有变小的时候,但整体的趋势是变大
拼接9,18,36这些数即可,例如9000000001800000036...
只要整体趋势是变大多,变小少,
且拼接的足够长,那么整体趋势一定是变大
代码
# def f(n):
# s = str(n)
# ans = 0
# for c in s:
# ans += ord(c) - ord('0')
# return anss = ''
for i in range(100):v = 5 ** is += str(v)
n = int(s)
print(n)
# for i in range(51):
# print(f"i:{i} f:{f(n)}")
# n*=2相关文章:
AtCoder Grand Contest 066 B. Decreasing Digit Sums(构造 打表找规律)
题目 给定一个n(n<50),记f(x)是x各数位的加和,例如f(331)3317 要求输出一个x(),且对于任意i∈[1,n],均有成立 思路来源 jiangly B站讲解 题解 首先n没啥用,构造一个n50成立的case即可, 给定一个x…...

Hadoop系列总结
一、Hadoop linux基本操作 前提掌握Linux基本操作 参考 Linux基本操作-CSDN博客 1、查看hadoop指定路径下文件大小前6的文件信息 hdfs dfs[hadoop fs] -du -h /path/to/directory|sort -hr|head -n 6...

【第三方登录】Twitter
创建应用 APPID 和 相关回调配置 重新设置api key 和 api secret 设置回调和网址 还有 APP的类型 拿到ClientID 和 Client Secret 源码实现 获取Twitter 的登录地址 public function twitterUrl() {global $db,$request,$comId;require "inc/twitter_client/twitte…...
)
C++经典面试题目(十七)
1、请解释拷贝构造函数的作用,并说明其调用时机。 拷贝构造函数是一种特殊的构造函数,用于创建一个新对象,其内容与另一个对象相同。它将一个已存在的对象作为参数,并使用该对象的值来初始化新创建的对象。拷贝构造函数的调用时机…...

DFS2 C++
一、指数型枚举 1、题目: 从 1∼n1∼ 这 n 个整数中随机选取任意多个,输出所有可能的选择方案。 输入格式 输入一个整数 n。 输出格式 每行输出一种方案。 同一行内的数必须升序排列,相邻两个数用恰好 11 个空格隔开。 对于没有选任何…...
2021-08-06
yarn的简介: Yarn是facebook发布的一款取代npm的包管理工具。 yarn的特点: 速度超快。 Yarn 缓存了每个下载过的包,所以再次使用时无需重复下载。 同时利用并行下载以最大化资源利用率,因此安装速度更快。超级安全。 在执行代码…...
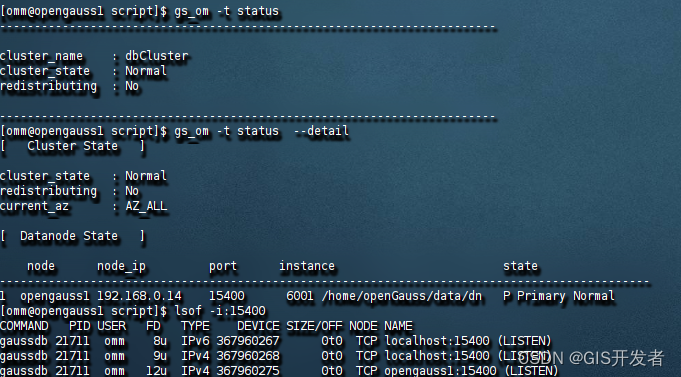
Centos服务器Open Gauss 部署
近期很多的项目由于信创要求使用一些国产的数据库,比如OpenGauss。OpenGuass是华为高斯DB的开源版,内核还是PostgreSQL,商业版是收费的。这里记录一下是如何安装部署 的。 官方中文文档 官方下载地址 部署要求 操作系统要求 ARMÿ…...

Vue与Electron融合之道:从Web App到桌面App的华丽转身
Vue与Electron融合之道:从Web App到桌面App的华丽转身 引言Vue 与 Electron 的天然契合共享技术栈高效开发与部署用户体验升级 Vue 与 Electron 融合实战初始化项目调整Vue项目结构利用 Electron API 增强功能定制桌面应用外观构建与部署 结语 引言 Vue.js 作为一款…...

Higress 基于自定义插件访问 Redis
作者:钰诚 简介 基于 wasm 机制,Higress 提供了优秀的可扩展性,用户可以基于 Go/C/Rust 编写 wasm 插件,自定义请求处理逻辑,满足用户的个性化需求,目前插件已经支持 redis 调用,使得用户能够…...

Mysql的库函数
MySQL是一个流行的开源关系型数据库管理系统,它提供了大量的内置库函数,用于在查询时执行各种操作。这些函数可以帮助开发者在数据检索、转换和处理过程中实现更复杂的逻辑。 1 字符串函数 函数描述ASCII(s)返回字符串 s 的第一个字符的 ASCII 码。CHA…...
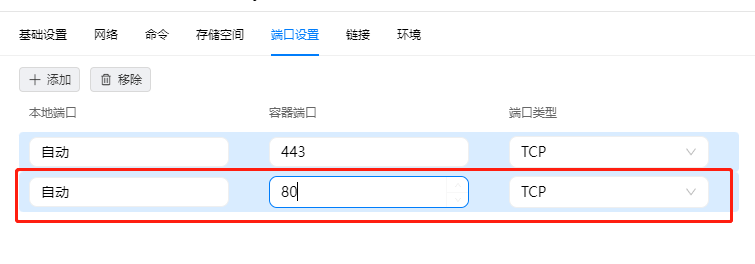
绿联 安装onlyoffice容器并启用Cloudreve的office在线预览与编辑功能
原文:绿联 安装onlyoffice容器并启用Cloudreve的office在线预览与编辑功能 本篇教程以配合Cloudreve扩展文档预览/编辑为目的编写,OnlyOffice的其他用途未深入研究也不做探讨,仅使用WOPI能力。 硬件要求 镜像大小:2.91Gb或更大 …...

金钱卦起卦
前言 本文目的: 1.了解什么是《易经》 2.了解什么是八卦/六十四卦 3.金钱卦起卦方法 4.如何解卦 一、什么是易经? 1、易经就是一本书、一本著作 2、它的成书经历了三个阶段 第一阶段:在5000多年前,由人类的始祖伏羲通过观察时…...

学透Spring Boot 003 —— Spring 和 Spring Boot 常用注解(附面试题和思维导图)
这是 学透 Spring Boot 专栏 的第三篇,欢迎关注我,与我一起学习和探讨 Spring Boot 相关知识,学透 Spring Boot。 从面试题说起 今天我们通过一道和Spring Boot有关的常见面试题入手。 面试题:说说 Spring Boot 中有哪些常用注解…...
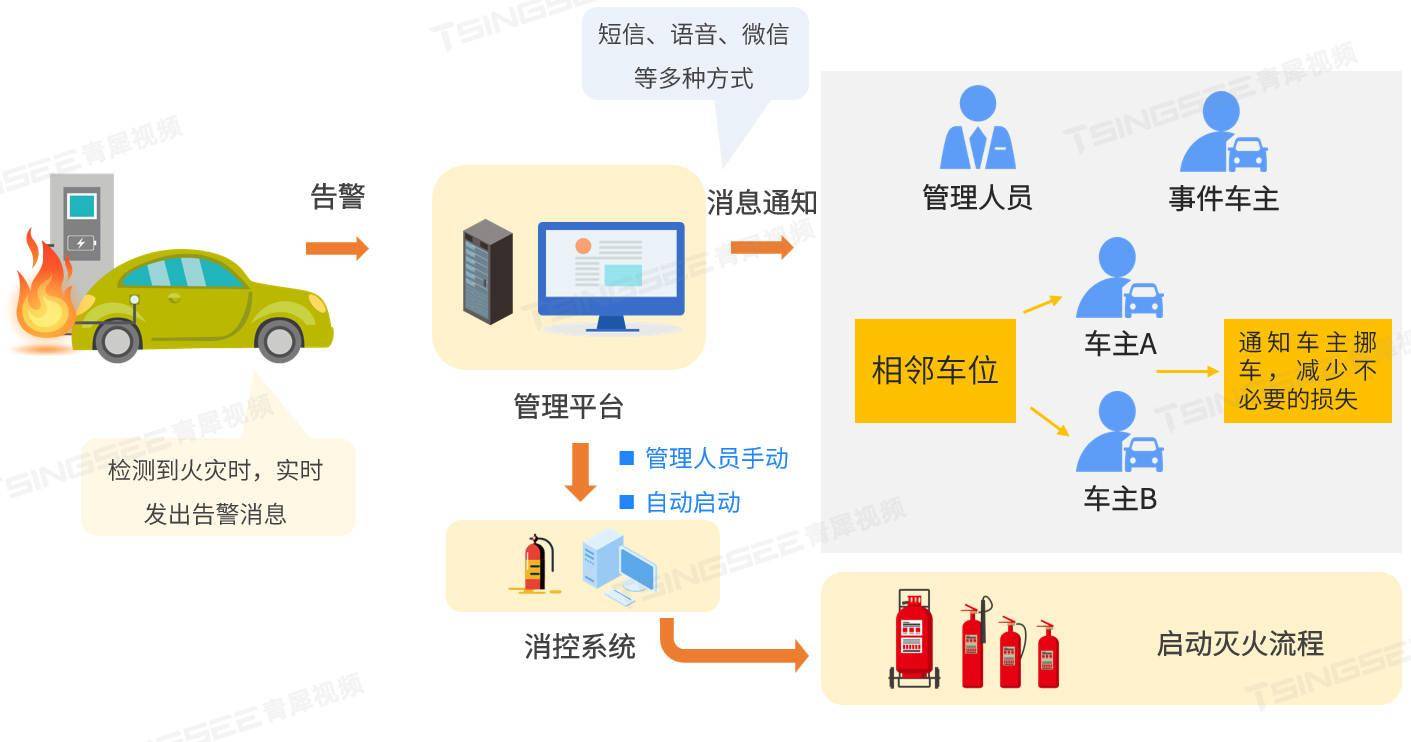
新能源汽车充电桩常见类型及充电桩站场的智能监管方案
随着新能源汽车市场的迅猛发展,充电桩作为支持其运行的基础设施,也呈现出多样化的类型。这些充电桩不仅在外形和功能上存在差异,更在充电速度、充电方式以及使用场景等方面展现出独特的优势。 一、充电桩类型及区别 1、慢充桩(交…...

让工作自动化起来!无所不能的Python
文章目录 前言一、Python是办公自动化的重要工具二、Python是提升职场竞争力的利器三、Python是企业数字化的重要平台四、Python是AI发展的重要通道之一编辑推荐内容简介作者简介目录前言为什么要写这本书 读者对象如何阅读本书赠书活动 前言 随着我国企业数字化和信息化的深入…...

Facebook轮播广告是什么?投放过程中有哪些需要注意的吗?
轮播广告是Facebook广告形式中的一种,可以把3—5个广告合并到一个可滚动的广告单元中。轮播广告会出现在新鲜事即News Feed中,是独立站卖家常用的一种广告形式 为什么选择轮播广告? 转化率更高:相较于单图广告,轮播广…...
3、jvm基础知识(三)
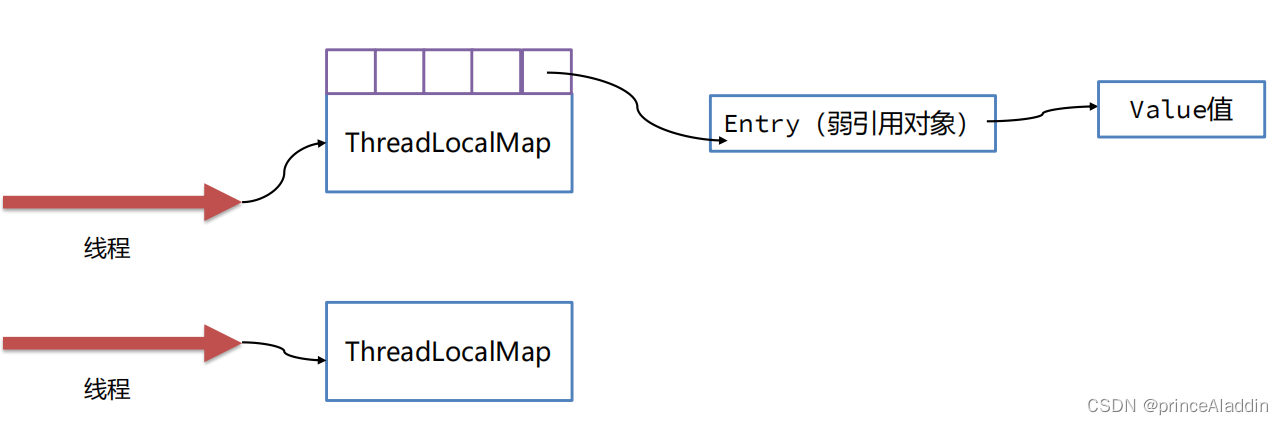
如何判断堆上的对象没有被引用? 常见的有两种判断方法:引用计数法和可达性分析法。 引用计数法会为每个对象维护一个引用计数器,当对象被引用时加1,取消引用时减1。 引用计数法的优点是实现简单,缺点有两点࿱…...

leetcode414-Third Maximum Number
这道题目求第三大数,如果第三大数不存在则返回最大数,且该数字最大值不超过2^31-1。从这个提示上就可以看出这个数字是用int类型表示的。我们当然可以通过排序的方式先给数组排序然后很容易的就能求解。但是有没有什么更好的办法呢?对于数组来…...
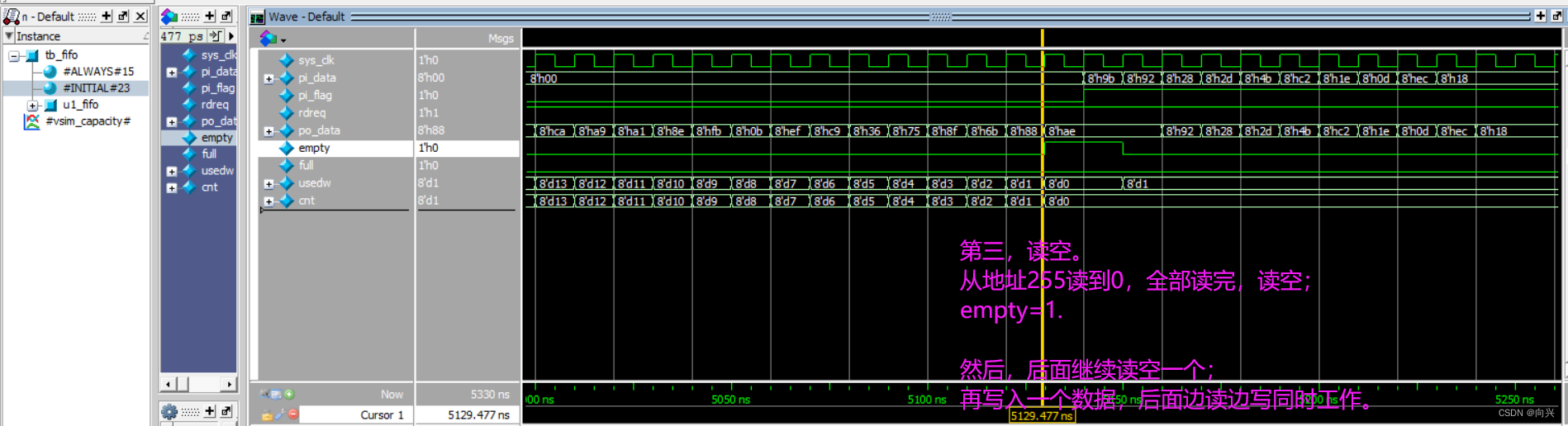
解决Quartus与modelsim联合仿真问题:# Error loading design解决,是tb文件中没加:`timescale 1ns/1ns
解决Quartus与modelsim联合仿真问题:# Error loading design解决,是tb文件中没加:timescale 1,一直走下来,在modelsim中出现了下面问题2,rtl文件、tb文件2.1,rtl代码2.2,tb测试2.3&a…...

vue使用elementui组件的的对话框;使用ref
1.第一步,先在父组件中引用,设置ref的值 <el-dialog :visible.sync"dialogEditVisible"append-to-body width"1000px" title"编辑":close-on-click-modal"false"><dialog-edit v-if"dialogEditV…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
