整型之韵,数之舞:大小端与浮点数的内存之旅
✨✨欢迎👍👍点赞☕️☕️收藏✍✍评论个人主页:秋邱’博客
所属栏目:人工智能
(感谢您的光临,您的光临蓬荜生辉)
1.0 整形提升
我们先来看看代码。
int main()
{char a = 3;char b = 127;char c = a + b;pritnf("%d", c);return 0;
}
这是char类型的相加,但你以为答案是130,那就是错了,事实没那么简单。
1.1 什么是整形提升
C语⾔中整型算术运算总是⾄少以缺省整型类型的精度来进⾏的。
为了获得这个精度,表达式中的字符和短整型操作数在使⽤之前被转换为普通整型,这种转换称为整
型提升。
1.2 如何整形提升?
规则:
- 有符号整数提升是按照变量的数据类型的符号位来提升的
- ⽆符号整数提升,⾼位补0
打印结果:
-126
分析
char a = 3;00000000000000000000000000000011 //3的二进制00000011 char achar b = 127;00000000000000000000000001111111 //127的二进制01000000 char bchar c = a + b;00000011 char a01000000 char b //这里还不能直接相加,要对a和b进行整形提升//在vs下char是有符号的char,所以对char a进行整形的提升,符号位是000000000000000000000000000000011 //char a的整形提升//同理,char b也是有符号的char,符号位是000000000000000000000000001111111 //char b的整形提升00000000000000000000000010000010 //a + b,d但是char c中只能存放8个比特位10000010 //char cprintf("%d", c);//%d是按十进制打印有符号的整数,但我们是char c,所以需要进行整形提升//char c是有符号数,最高位是1全补1.11111111111111111111111110000010 //char c整形提升的结果(补码)//打印的方式是原码,我们要对c补码进行,取反+100000000000000000000000001111110 //原码//结果是-127
1.3 整形提升的意义
表达式的整型运算要在CPU的相应运算器件内执⾏,CPU内整型运算器(ALU)的操作数的字节⻓度⼀般就是int的字节⻓度,同时也是CPU的通⽤寄存器的⻓度。因此,即使两个char类型的相加,在CPU执⾏时实际上也要先转换为CPU内整型操作数的标准⻓ 度。 通⽤CPU(general-purposeCPU)是难以直接实现两个8⽐特字节直接相加运算(虽然机器指令中可能有这种字节相加指令)。所以,表达式中各种⻓度可能⼩于int⻓度的整型值,都必须先转换为 int或unsigned int,然后才能送⼊CPU去执⾏运算。
也就是说,小于整形的类型就要进行提升。
注意:char的是unsigned char 还是 signed char ,这是不确定的,而是取决于编译器。
但常见的编译器上char 一般都是signed char。
2.0 算术转换
如果某个操作符的各个操作数属于不同的类型,那么除⾮其中⼀个操作数的转换为另⼀个操作数的类
型,否则操作就⽆法进⾏。下⾯的层次体系称为寻常算术转换。
long double
double
float
unsigned long int
long int
unsigned int
int
如果某个操作数的类型在上⾯这个列表中排名靠后,那么⾸先要转换为另外⼀个操作数的类型后执⾏
运算。
3.0 大小端
3.1 什么是大小端
大端小端是计算机存储数据的一种方式。在内存中,数据被分割为多个字节进行存储。大小端指的是字节的存储顺序。
大端存储是指高位字节被存储在低位地址,低位字节存储在高位地址。大端存储方式常用于网络协议中。
小端存储是指低位字节被存储在低位地址,高位字节存储在高位地址。小端存储方式常用于x86架构的计算机。
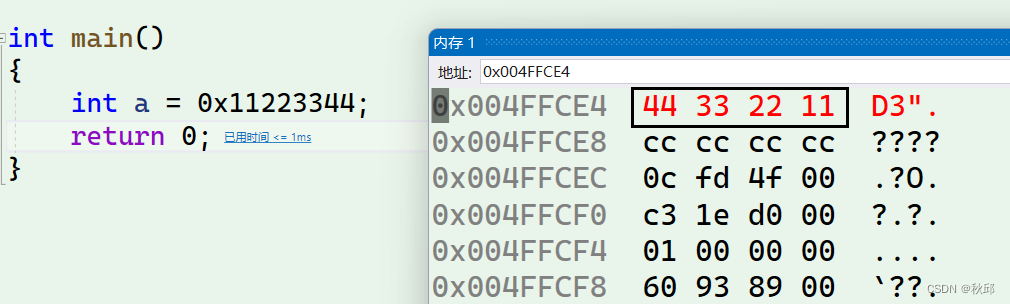 我们在vs2022提示可知,vs2022中采用的是小端存储的方式。
我们在vs2022提示可知,vs2022中采用的是小端存储的方式。
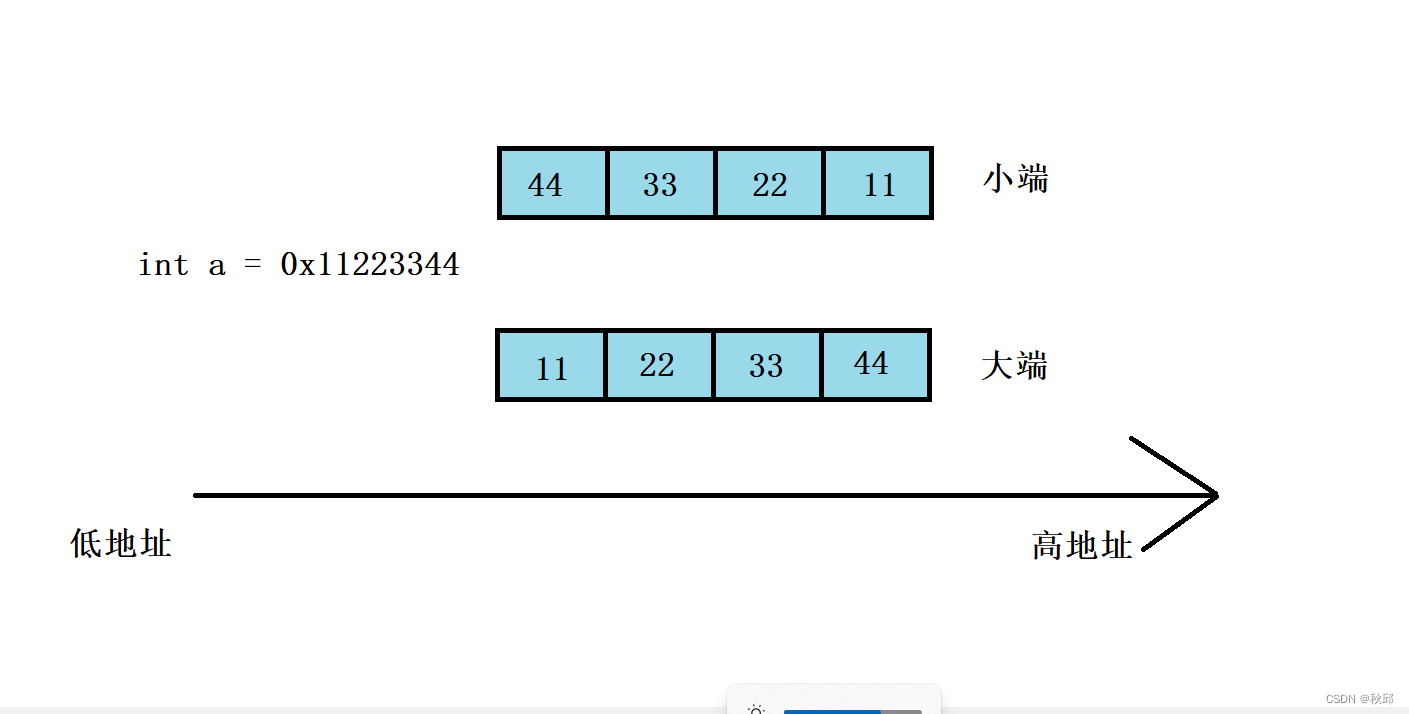
接下里我们用程序来判断vs2022里的是大端还是小端。
3.2 判断大小端
3.2.1指针判断
#include<stdio.h>
int check_sys()
{int i = 1;return *(char*)&i;}
int main()
{int ret = check_sys();if (ret == 1){printf("小端");}else{printf("大端");}return 0;
}
3.2.2联合体判断
int check_sys()
{union check {char j;int i;};union check u = { 0 };u.j = 1;return u.j;}
int main()
{int ret = check_sys();if (ret == 1){printf("小端");}else{printf("大端");}return 0;
}
打印结果:
小端
3.3大小端的意义
我们知道了大小端,然后有什么用呢?
- 确保数据传输的准确性:在不同系统或设备之间进行数据交换时,了解大小端可以确保数据被正确解释。
- 兼容不同的系统:有助于软件在各种平台上的移植和运行。
- 优化性能:根据大小端特点进行针对性的优化。
- 调试和排错:当出现数据解析问题时,能更快地定位问题。
- 理解系统架构:加深对计算机系统内部工作原理的理解。
- 网络通信:确保网络协议的正确实现和数据的无误传输。
- 硬件设计:对硬件设计和开发具有指导意义。
- 数据恢复:在数据恢复过程中,正确解读存储的数据。
- 提高编程效率:避免因大小端问题导致的错误。
- 增强系统安全性:防止因数据解读错误引发的安全漏洞。
两种存储方式的区别在于字节的存储顺序,对于单个字节的操作没有影响,但对于多个字节的数据,如整数和浮点数,字节顺序的不同会导致数据的解释和处理方式不同。因此,当不同大小端的计算机之间进行数据传输时,需要进行字节序的转换。
4.0浮点数在内存中的存储
浮点数在内存中的存储是怎么样的呢,跟整形的存储一样吗?答案:不是!接下里往下看。
4.1 浮点数的存储
根据国际标准IEEE(电⽓和电⼦⼯程协会)754,任意⼀个⼆进制浮点数V可以表⽰成下⾯的形式:
V = (−1) ^S*M *2^E
• (-1)^S 表⽰符号位,当S=0,V为正数;当S=1,V为负数
• M表⽰有效数字,M是⼤于等于1,⼩于2的
• 表⽰指数位
二进制对应的十进制图
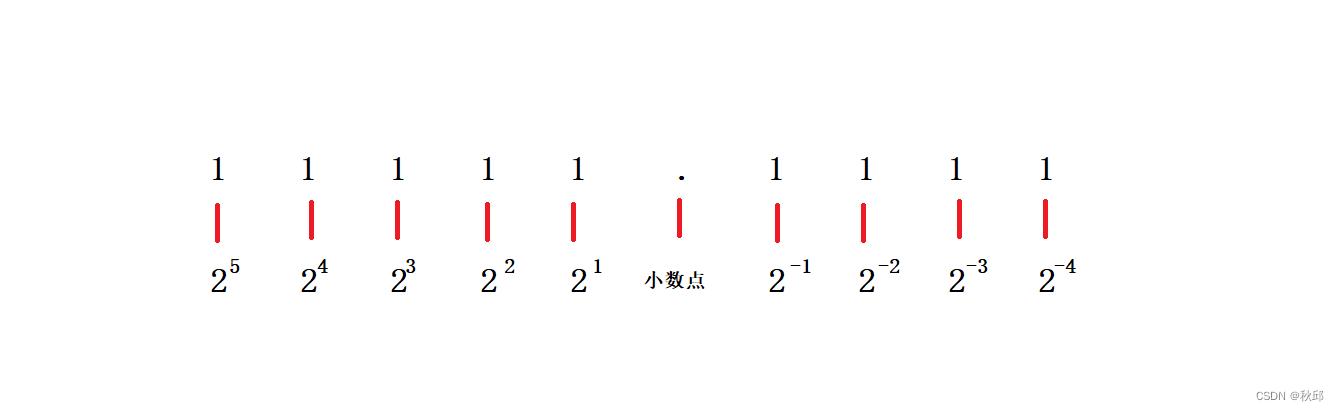
举例
⼗进制的5.0,写成⼆进制是101.0 ,相当于1.01×2^2 。
那么,按照上⾯V的格式,可以得出S=0,M=1.01,E=2。
⼗进制的-5.0,写成⼆进制是-101.0 ,相当于-1.01×2^2 。那么,S=1,M=1.01,E=2。
IEEE 754规定:
对于32位的浮点数,最⾼的1位存储符号位S,接着的8位存储指数E,剩下的23位存储有效数字M对于64位的浮点数,最⾼的1位存储符号位S,接着的11位存储指数E,剩下的52位存储有效数字M。
4.2 浮点数存的过程
IEEE 754对有效数字M和指数E,还有⼀些特别规定。
对于M
1≤M<2 ,也就是说,M可以写成1.xxxxxx 的形式,其中xxxxxx
表⽰⼩数部分。IEEE 754规定,在计算机内部保存M时,默认这个数的第⼀位总是1,因此可以被舍去,只保存后⾯的xxxxxx部分。⽐如保存1.01的时候,只保存01,等到读取的时候,再把第⼀位的1加上去。这样做的⽬的,是节省1位有效数字。以32位浮点数为例,留给M只有23位,将第⼀位的1舍去以后,等于可以保存24位有效数字。
对于E
,E为⼀个⽆符号整数(unsignedint)
这意味着,如果E为8位,它的取值范围为0255;如果E为11位,它的取值范围为02047。但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE754规定,存⼊内存时E的真实值必须再加上⼀个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。⽐如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
4.3 浮点数取的过程
指数E取出内存,情况有三。
1.E不全为0或不全为1
这时,浮点数就采⽤下⾯的规则表⽰,即指数E的计算值减去127(或1023),得到真实值,再将有效数字M前加上第⼀位的1。
⽐如:0.5的⼆进制形式为0.1,由于规定正数部分必须为1,即将⼩数点右移1位,则为1.0*2^(-1),其阶码为-1+127(中间值)=126,表⽰为01111110,⽽尾数1.0去掉整数部分为0,补⻬0到23位00000000000000000000000,则其⼆进制表⽰形式为:
0 01111110 00000000000000000000000
2.E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值,有效数字M不再加上第⼀位的1,⽽是还原为0.xxxxxx的⼩数。这样做是为了表⽰±0,以及接近于0的很⼩的数字。
0 00000000 00100000000000000000000
3.E全为1
这时,如果有效数字M全为0,表⽰±⽆穷⼤(正负取决于符号位s);
0 11111111 00010000000000000000000
相关文章:

整型之韵,数之舞:大小端与浮点数的内存之旅
✨✨欢迎👍👍点赞☕️☕️收藏✍✍评论 个人主页:秋邱’博客 所属栏目:人工智能 (感谢您的光临,您的光临蓬荜生辉) 1.0 整形提升 我们先来看看代码。 int main() {char a 3;char b 127;char …...

变量作用域
变量作用域 标识符的作用域是定义为其声明在程序里的可应用范围, 或者即是我们所说的变量可见性。换句话说,就好像在问你自己,你可以在程序里的哪些部分去访问一个制定的标识符。变量可以是局部域或者全局域。 全局变量与局部变量 定义在函数内的变量有局部作用域,在一个…...
数据结构:链表的双指针技巧
文章目录 一、链表相交问题二、单链表判环问题三、回文链表四、重排链表结点 初学双指针的同学,请先弄懂删除链表的倒数第 N 个结点。 并且在学习这一节时,不要将思维固化,认为只能这样做,这里的做法只是技巧。 一、链表相交问题 …...

用WHERE命令可以在命令行搜索文件
文章目录 用WHERE命令可以在命令行搜索文件概述笔记没用的小程序END 用WHERE命令可以在命令行搜索文件 概述 想确认PATH变量中是否存在某个指定的程序(具体是在PATH环境变量中给出的哪个路径底下?). 开始不知道windows有where这个命令, 还自己花了2个小时写了一个小程序. 后…...

持续交付/持续部署流水线介绍(CD)
目录 一、概述 二、典型操作流程 2.1 CI/CD典型操作流 2.2 CI/CD操作流程说明 2.3 总结 三、基于GitHubDocker的持续交付/持续部署流水线(公有云) 3.1 基于GitHubDocker的持续交付/持续部署操作流程示意图 3.2 GitHubDocker持续交付/持续部署流水…...

第四百三十八回
文章目录 1. 概念介绍2. 思路与方法2.1 实现思路2.2 实现方法 3. 示例代码4. 内容总结 们在上一章回中介绍了"不同平台上换行的问题"相关的内容,本章回中将介绍如何在页面上显示蒙板层.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们…...

Python学习:面相对象
面向对象 面向对象技术简介 类(Class): 用来描述具有相同的属性和方法的对象的集合。它定义了该集合中每个对象所共有的属性和方法。对象是类的实例。方法:类中定义的函数。类变量:类变量在整个实例化的对象中是公用的。类变量定义在类中且在函数体之外。类变量通常不作为实…...
SSM学习——Spring AOP与AspectJ
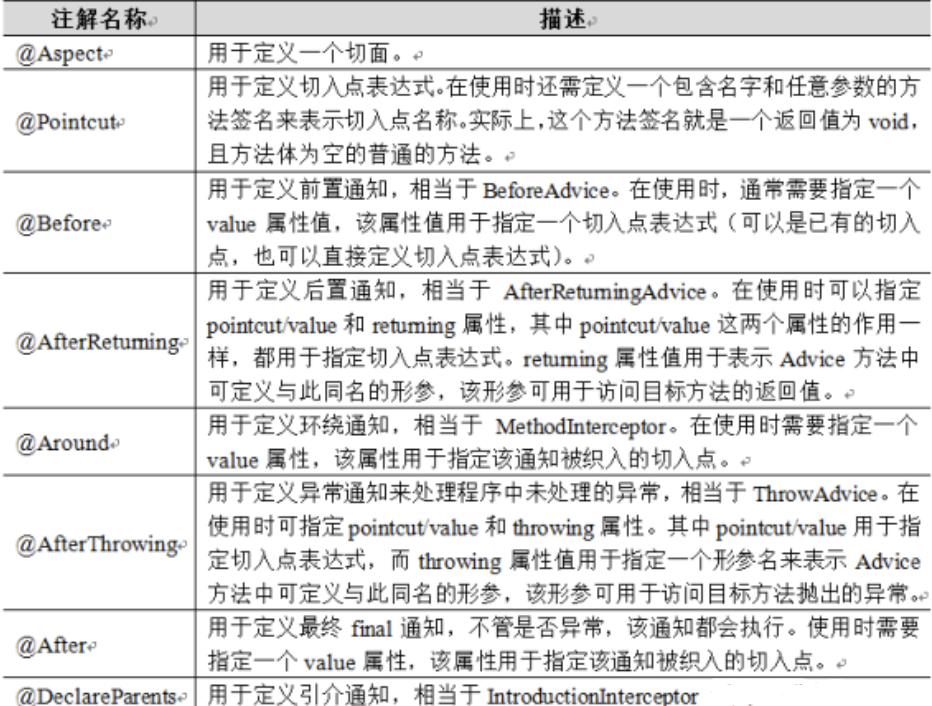
Spring AOP与AspectJ 概念 AOP的全称为Aspect-Oriented Programming,即面向切面编程。 想象你是汉堡店的厨师,每一份汉堡都有好几层,这每一层都可以视作一个切面。现在有一位顾客想要品尝到不同风味肉馅的汉堡,如果按照传统的方…...

Android 使用LeakCanary检测内存泄漏,分析原因
内存泄漏是指无用对象(不再使用的对象)持续占有内存或无用对象的内存得不到及时释放,从而造成内存空间的浪费称为内存泄漏。 平时我们在使用app时,少量的内存泄漏我们是发现不了的,但是当内存泄漏达到一定数量时&…...
Linux部署Kafka2.8.1
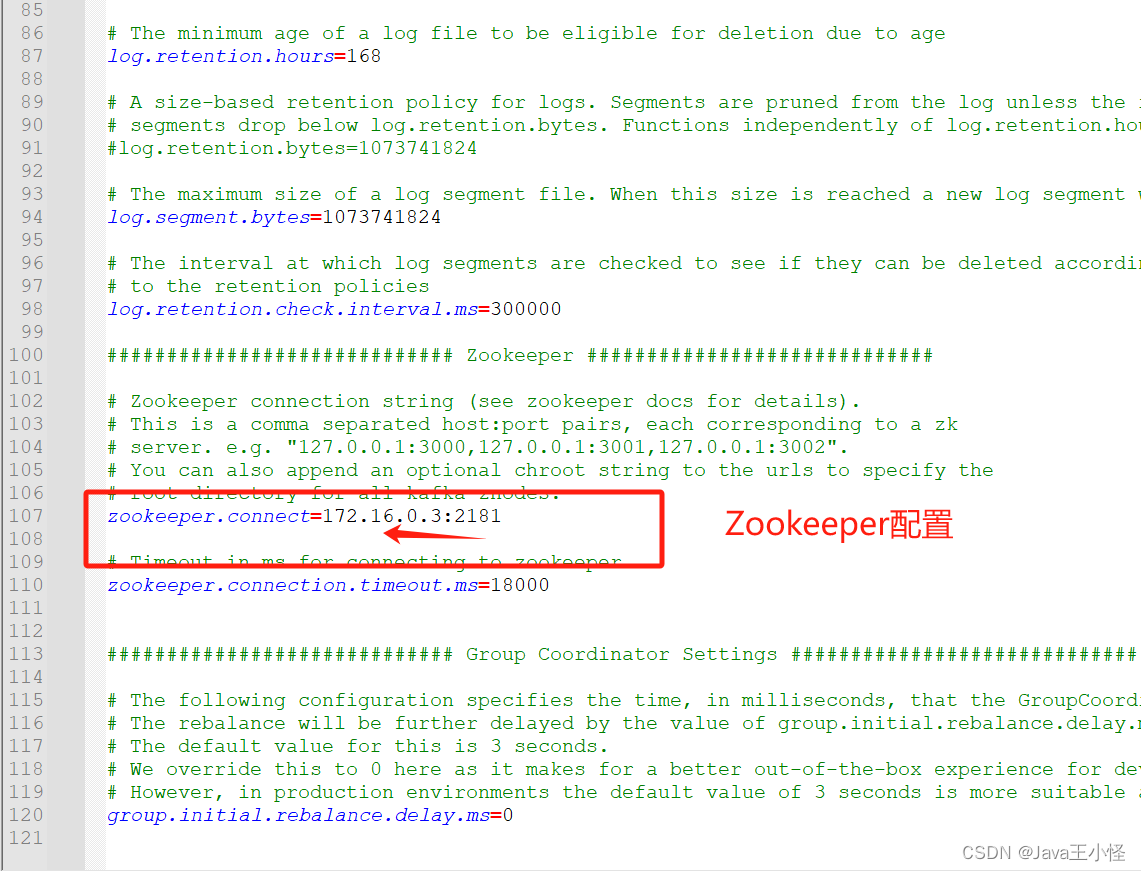
安装Jdk 首先确保你的机器上安装了Jdk,Kafka需要Java运行环境,低版本的Kafka还需要Zookeeper,我此次要安装的Kafka版本为2.8.1,已经内置了一个Zookeeper环境,所以我们可以不部署Zookeeper直接使用。 1、解压Jdk包 t…...
【pytest、playwright】allure报告生成视频和图片
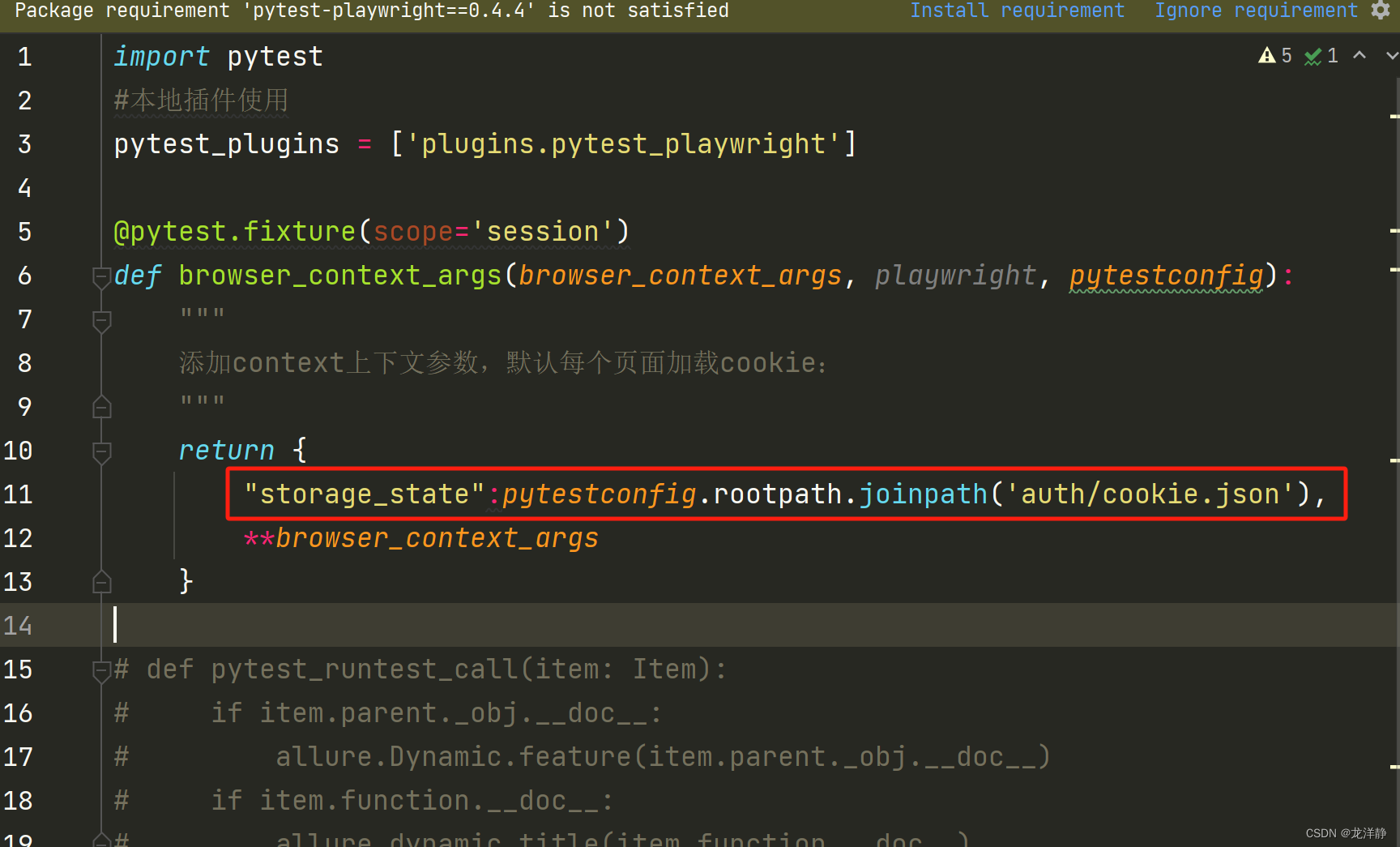
目录 1、修改插件pytest_playwright 2、conftest.py配置 3、修改pytest.ini文件 4、运行case 5、注意事项 1、修改插件pytest_playwright pytest_playwright.py内容如下: # Copyright (c) Microsoft Corporation. # # Licensed under the Apache License, Ver…...
浅谈iOS开发中的自动引用计数ARC
1.ARC是什么 我们知道,在C语言中,创建对象时必须手动分配和释放适量的内存。然而,在 Swift 中,当不再需要类实例时,ARC 会自动释放这些实例的内存。 Swift 使用 ARC 来跟踪和管理应用程序的内存,其主要是由…...

Spring IoCDI(2)
IoC详解 通过上面的案例, 我们已经知道了IoC和DI的基本操作, 接下来我们来系统地学习Spring IoC和DI的操作. 前面我们提到的IoC控制反转, 就是将对象的控制权交给Spring的IoC容器, 由IoC容器创建及管理对象. (也就是Bean的存储). Bean的存储 我们之前只讲到了Component注解…...

30. UE5 RPG GamplayAbility的配置项
在上一篇文章,我们介绍了如何将GA应用到角色身上的,接下来这篇文章,将主要介绍一下GA的相关配置项。 在这之前,再多一嘴,你要能激活技能,首先要先应用到ASC上面,才能够被激活。 标签 之前介绍…...

提升自己最快的方式是什么?
提升自己最快的方式通常涉及到个人成长的各个方面,包括心理、情感、技能和知识等。根据查阅到的资料,以下是一些具体的方法和步骤,帮助你快速提升自己: 1. 培养屏蔽力 荷兰畅销书作家罗伊马丁纳提到,屏蔽力是个人成长…...

题目:一个5位数,判断它是不是回文数。即12321是回文数,个位与万位相同,十位与千位相同。
题目:一个5位数,判断它是不是回文数。即12321是回文数,个位与万位相同,十位与千位相同。 There is no nutrition in the blog content. After reading it, you will not only suffer from malnutrition, but also impotence…...

《HelloGitHub》第 96 期
兴趣是最好的老师,HelloGitHub 让你对编程感兴趣! 简介 HelloGitHub 分享 GitHub 上有趣、入门级的开源项目。 https://github.com/521xueweihan/HelloGitHub 这里有实战项目、入门教程、黑科技、开源书籍、大厂开源项目等,涵盖多种编程语言 …...
C++tuple类型
tuple 类型 tuple是类似pair的模板。 每个pair的成员类型都不相同,但每个pair都恰好有两个成员。不同tuple类型的成员类型也不相同,但一个tuple可以有任意数量的成员。 每个确定的tuple类型的成员数目是固定的,但一个tuple类型的成员数目可…...

亚远景科技-浅谈ASPICE标准和ASPICE认证/评估
ASPICE(Automotive SPICE)是一种针对汽车行业的软件开发过程的评估模型,它旨在帮助汽车制造商和供应商提高软件开发过程的能力和质量,从而提升产品的质量、安全性和效率。 ASPICE标准涵盖了软件开发的各个阶段和活动,…...

PHP性能提升方案
一、背景与介绍 PHP语言开发效率高,特别应用于适合中小型项目,对于创业初期敏捷开发验证项目可行性或者Demo演示绝对占据优势。 但是随着现在Web应用的复杂性,针对项目要适应高并发、高流量的访问特性,PHP确实在性能方面相对Go、J…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

