【面试经典150 | 动态规划】最小路径和
文章目录
- 写在前面
- Tag
- 题目来源
- 解题思路
- 方法一:动态规划
- 方法二:空间优化
- 写在最后
写在前面
本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更……
专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行回顾与总结,文章结构大致如下,部分内容会有增删:
- Tag:介绍本题牵涉到的知识点、数据结构;
- 题目来源:贴上题目的链接,方便大家查找题目并完成练习;
- 题目解读:复述题目(确保自己真的理解题目意思),并强调一些题目重点信息;
- 解题思路:介绍一些解题思路,每种解题思路包括思路讲解、实现代码以及复杂度分析;
- 知识回忆:针对今天介绍的题目中的重点内容、数据结构进行回顾总结。
Tag
【动态规划-空间优化】【数组】
题目来源
64. 最小路径和

解题思路
方法一:动态规划
定义状态
朴素的动态规划方法是定义状态 dp[i][j],表示从网格左上角 (0, 0) 位置到 (i, j) 位置的最小路径和。
状态转移
根据题目中 “每次只能向下或者向右移动一步”,可知到达位置 (i, j) 只能从 (i-1, j) 向下移动一步或者从 (i, j-1) 向右一步,因此有转移关系:
d p [ i ] [ j ] = m i n ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] ) , i ≥ 1 , j ≥ 1 dp[i][j] = min(dp[i-1][j], dp[i][j-1]), i \ge 1, j \ge 1 dp[i][j]=min(dp[i−1][j],dp[i][j−1]),i≥1,j≥1
base case
dp[0][0] = grid[0][0]。
对于网格 grid 中的第一行和第一列位置,只能从对应位置的左侧和上方的位置移动一步得到,于是需要进行如下方式的初始化:
// 第一列
for (int i = 1; i < m; ++i)dp[i][0] = dp[i - 1][0] + grid[i][0];// 第一行
for (int j = 1; j < n; ++j) {dp[0][j] = dp[0][j - 1] + grid[0][j];
}
最后返回
dp[m-1][n-1] 表示从网格左上角到网格右下角的最小路径和。
实现代码
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<vector<int>> dp = vector<vector<int>>(m, vector<int>(n));dp[0][0] = grid[0][0];// 对于在第一行或者第一列第一列for (int i = 1; i < m; ++i)dp[i][0] = dp[i - 1][0] + grid[i][0];第一行for (int j = 1; j < n; ++j) {dp[0][j] = dp[0][j - 1] + grid[0][j];}// 对于不在第一行和第一列的元素for (int i = 1; i < m; ++i) {for (int j = 1; j < n; ++j) {dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];}}return dp[m - 1][n - 1];}
};
复杂度分析
时间复杂度: O ( m n ) O(mn) O(mn), m m m 为网格 grid 的行数, n n n 为网格的列数。
空间复杂度: O ( m n ) O(mn) O(mn)。
方法二:空间优化
方法一中朴素解法的空间复杂度可以进行优化,只需要使用 O ( m i n { m , n } ) O(min\{m, n\}) O(min{m,n}) 的复杂度即可解决。
我们以 示例 1 为例说明,如何使用线性空间解决本题。
网格的行数和列数一样,选择按行来更新最小路径和(选择列也可以),维护一个数组 dp 长度为 3。
初始化 dp = {1, 4, 5},dp[0] 表示从位置 (0, 0) 到位置 (0, 0) 的最小路径和;dp[1] 表示从位置 (0, 0) 到位置 (0, 1) 的最小路径和;dp[2] 表示从位置 (0, 0) 到位置 (0, 2) 的最小路径和。
在网格的第一行(从 0 开始数),dp[0] 表示从位置 (0, 0) 到位置 (1, 0) 的最小路径和,因为只能从 (0, 0) 位置到 (1, 0) 位置,所以更新 dp[0] = dp[0] + grid[1][0];dp[1] 表示从位置 (0, 0) 到位置 (1, 1) 的最小路径和,因为可以从 (1, 0) 位置向右或者 (0, 1) 位置向下移动到位置 (1, 1),所以有 dp[1] = min(dp[0], dp[1]) + grid[i][j]…
具体实现见如下代码。
实现代码
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m = grid.size();int n = grid[0].size();int more = max(m, n);int less = min(m, n);bool rowMore = more == m; // 判断是否是行数大于等于列数vector<int> arr(less); // 以较短维度的长度作为临时空间,比如列数较小int i, j;for (i = 0; i < less; ++i) {// 更新第 0 行的所有列,即初始化if (i == 0) {arr[i] = grid[0][0];}else {arr[i] = arr[i - 1] + (rowMore ? grid[0][i] : grid[i][0]);}}for (i = 1; i < more; ++i) {// 按照行进行更新arr[0] = arr[0] + (rowMore ? grid[i][0] : grid[0][i]); // 更新 i 行 0 列的答案for (j = 1; j < less; ++j) { // 更新 i 行其他列的答案arr[j] = min(arr[j - 1], arr[j]) + (rowMore ? grid[i][j] : grid[j][i]);}}return arr[less-1];}
};
复杂度分析
时间复杂度: O ( m n ) O(mn) O(mn), m m m 为网格 grid 的行数, n n n 为网格的列数。
空间复杂度: O ( m i n { m , n } ) O(min\{m, n\}) O(min{m,n})。
写在最后
如果您发现文章有任何错误或者对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度的方法,欢迎评论区交流。
最后,感谢您的阅读,如果有所收获的话可以给我点一个 👍 哦。
相关文章:

【面试经典150 | 动态规划】最小路径和
文章目录 写在前面Tag题目来源解题思路方法一:动态规划方法二:空间优化 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对于本题…...

生成式AI的情感实验——AI能否产生思想和情感?
机器人能感受到爱吗?这是一个很好的问题,也是困扰了科学家们很多年的科学未解之谜。虽然我们尚未准备好向智能机器赋予情感,但智能机器却已经可以借助生成式人工智能(AI)来帮助我们表达自己的情感。 自然情感表达 AI正…...

力扣贪心算法--第一天
前言 今天是贪心算法的第一天,算法之路重新开始! 内容 之前没了解过贪心算法。 什么是贪心 贪心的本质是选择每一阶段的局部最优,从而达到全局最优。难点就是如何通过局部最优,推出整体最优。 一、455.分发饼干 假设你是一…...
Nginx反向代理和缓存
一、Nginx反向代理 1.调度和代理的区别: 1.调度基于内核层面,代理基于应用层面 2.代理必须实现一手托两家 3.调度不需要监听任何端口,不需要工作任何应用程序,代理需要工作和上游服务器一模一样的进程 4.调度没有并发上限&am…...

支持多元AI场景应用,宁畅“NEX AI Lab”开放试用预约中
3月29日,宁畅在京举行发布会,正式发布“全局智算”战略,并在会上推出战略性新品“AI算力栈”,旨在有效解决大模型产业落地的全周期问题。 据宁畅CTO赵雷介绍,“AI算力栈”集成了宁畅在AI计算领域的软硬件能力ÿ…...

Git 如何合并多个连续的提交
我平常的编程喜欢是写一段代码就提交一次,本地一般不攒代码,生怕本地有什么闪失导致白干。但这样就又导致一个问题:查看历史日志时十分不方便,随便找一段提交可以看到: > git log --oneline 8f06be5 add 12/qemu-h…...

k8s 基础入门
1.namespace k8s中的namespace和docker中namespace是两码事,可以理解为k8s中的namespace是为了多租户,dockers中的namespace是为了网络、资源等隔离 2.deployment kubectl create #新建 kubectl aply #新建 更新 升级: 滚动升级&#x…...
【Python项目】AI动物识别工具
目录 背景 技术简介 系统简介 界面预览 背景 成像技术在全球科技发展中扮演了关键角色。在科学研究领域,拍摄所得的图像成为了一种不可或缺的研究工具。特别是在生态学与动物学研究中,鉴于地球的广阔地域和多样的气候条件,利用图像技术捕…...
详解)
逻辑回归(Logistic Regression)详解
逻辑回归是一种用于解决二分类问题的统计方法,它通过构建一个模型来预测某个事件的概率。 以下是逻辑回归的一些关键要点: 适用场景:逻辑回归特别适合于处理二分类问题,即两个类别的分类问题,例如判断一封邮件是否为…...

.vimrc文件的语句语法
本文结构: a、简介 b、详细解释其中的一些常见语句和语法。 a、.vimrc 文件是 Vim 编辑器用于配置用户设置和自定义行为的文件。当 Vim 启动时,它会读取 .vimrc 文件中的命令和设置,并根据这些指令来配置编辑器的行为。 b、.vimrc 文件中…...

c语言之函数指针作形参
在一些c语言的大工程中,会在定义的函数中,把一些其他函数指针作为本函数形参。 函数指针作形参的例子 代码如下: #include<stdio.h> int max(int a,int b) { return(a>b?a:b); } int min(int a,int b) { return(a<b?a:b); } i…...

python文件的读取操作
打开文件 fopen("F:/python/helloworld/测试.txt","r",encoding"UTF-8")读取文件 print(f"读取10个字节的结果{f.read(10)}") print(f"读取全部字节的结果{f.read()}") linesf.readlines() print(f"{lines}")读…...

查看并设定【网络适配器】的优先级(跃点数)
目录 前言: 1.查看所有的适配器 2.修改优先级(需要以管理员身份运行) 跃点数(InterfaceMetric ) DHCP 3.修改后的效果 pwoerShell 再次运行之前的程序 4.其他 参考 网络适配器1,8相关知识介绍1 …...
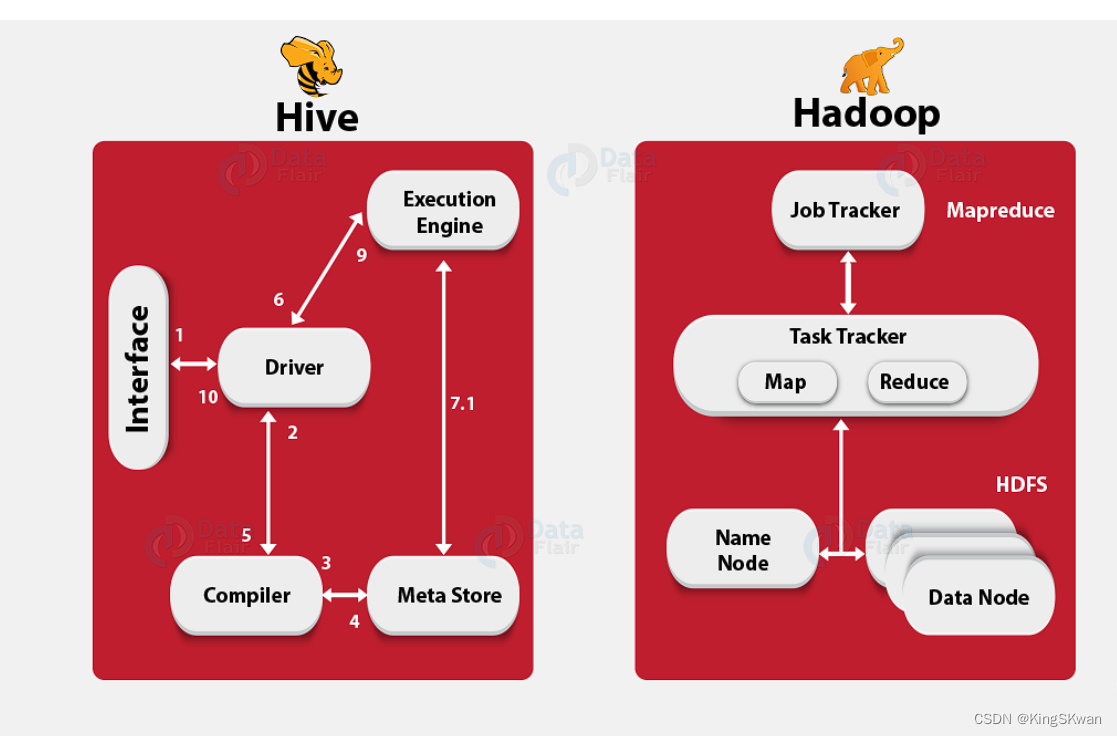
深入理解 Hadoop 上的 Hive 查询执行流程
在 Hadoop 生态系统中,Hive 是一个重要的分支,它构建在 Hadoop 之上,提供了一个开源的数据仓库系统。它的主要功能是查询和分析存储在 Hadoop 文件中的大型数据集,包括结构化和半结构化数据。Hive 在数据查询、分析和汇总方面发挥…...

JS封装网页进入/退出全屏功能,兼容各大主流浏览器
1、演示 2、封装进入全屏函数 mozRequestFullScreen:兼容Firefox webkitRequestFullscreen:兼容 Chrome、Safari、Opera msRequestFullscreen:兼容:IE/Edge const enter () > {const element document.documentElementif (el…...

el-table的复选框勾选整行变色
要实现el-table的复选框勾选整行变色,你可以使用element-ui提供的row-class-name属性结合scoped slot来完成。 首先,你需要为el-table组件添加 row-class-name 属性,并给它绑定一个方法。在这个方法中,你可以根据你的业务逻辑来判…...

一步一步写线程之八线程池的完善之二数据结构封装
一、数据容器 在前面分析过,不管是线程任务的封装还是同步数据队列的封装,都是需要一个数据结构的。一用来说,如果没有什么特殊的原因,开发者都是使用STL中数据结构。比如前面经常见到的std::queue,std::deque,std::vector,std::…...

go连接数据库(原生)
根据官网文档 Go Wiki: SQL Database Drivers - The Go Programming Language 可以看到go可以连接的关系型数据库 常用的关系型数据库基本上都支持,下面以mysql为例 下载mysql驱动 打开上面的mysql链接 GitHub - go-sql-driver/mysql: Go MySQL Driver i…...
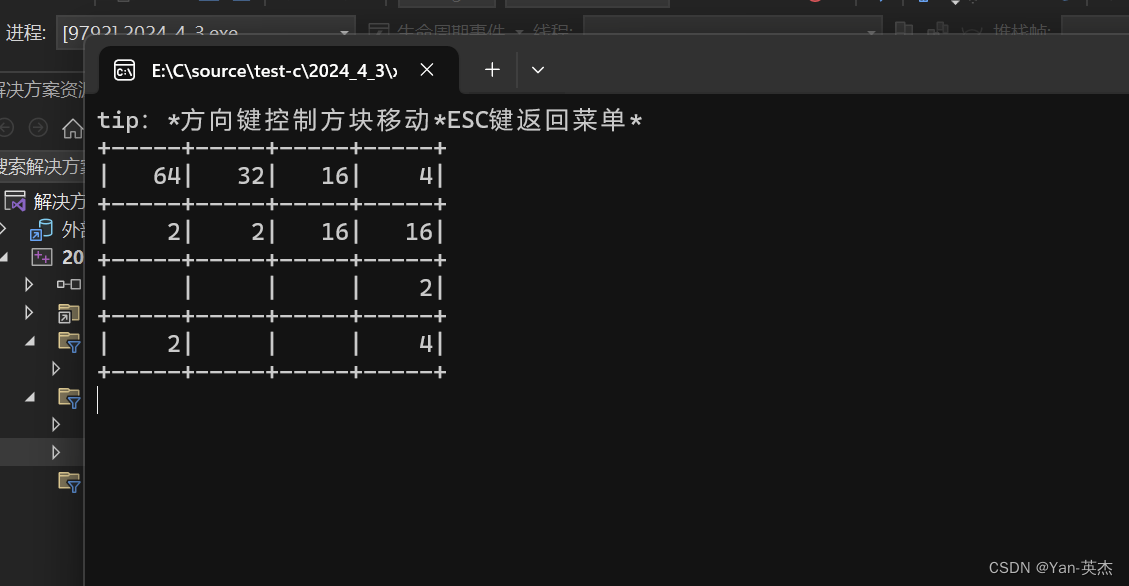
【C语言】2048小游戏【附源码】
欢迎来到英杰社区https://bbs.csdn.net/topics/617804998 一、游戏描述: 2048是一款数字益智类游戏,玩家需要使用键盘控制数字方块的移动,合并相同数字的方块,最终达到数字方块上出现“2048”的目标。 每次移动操作,所…...
部署项目遇到的各种问题总结
文章目录 前言一、后端问题 jar包运行出现错误宝塔面板使用jdk17二、数据库问题 版本问题三、前端问题 连不上后端总结 前言 在做完项目之后,为了让别人访问到自己的网站,就需要部署前端后端以及数据库,但是在部署的过程中出现了各种问题和困…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
