计算机视觉之三维重建(6)---多视图几何(上)
文章目录
- 一、运动恢复结构问题(SfM)
- 二、欧式结构恢复
- 2.1 概述
- 2.2 求解
- 2.3 欧式结构恢复歧义
- 三、仿射结构恢复
- 3.1 概述
- 3.2 因式分解法
- 3.3 总结
- 3.4 仿射结构恢复歧义
一、运动恢复结构问题(SfM)
1. 运动恢复结构问题:通过三维场景的多张图像,恢复出该场景的三维结构信息以及每张图片对应的摄像机参数。

2. 运动恢复问题建模表述:已知 n n n 个世界坐标点在 m m m 张图像中的对应点的像素坐标 x i j x_{ij} xij,计算出 m m m 个摄像机的投影矩阵 M i M_i Mi 和 n n n 个三维点 X j X_j Xj 的坐标。下图中 M = K [ R , T ] M=K[R,T] M=K[R,T]。

二、欧式结构恢复
2.1 概述
1. 欧式结构恢复问题:摄像机内参数已知,外参数未知情况。
2. 对于欧式结构恢复问题,已知摄像机内参数,根据投影矩阵的计算公式可知 x i j = M i X j = K i [ R i , T i ] X j x_{ij}=M_iX_j=K_i[R_i,T_i]X_j xij=MiXj=Ki[Ri,Ti]Xj。那么求解投影矩阵 M M M 只需要求解外参数 [ R , T ] [R,T] [R,T]。

2.2 求解
1. 对于二视图的欧式结构恢复问题,如果把世界坐标系放在第一个坐标系下面,那摄像机 1 1 1 的外参数为 [ I , 0 ] [I,0] [I,0],而摄像机 2 2 2 的外参数 [ R , T ] [R,T] [R,T] 却是未知的。

2. 求解步骤:
(1)求解基础矩阵 F F F(归一化八点法)
(2)求解本质矩阵 E = K 2 T F K 1 E=K_2^TFK_1 E=K2TFK1
(3)分解本质矩阵 E → R , T E \rightarrow R,T E→R,T
(4)三角化(求解世界坐标系下的3D坐标)

3. 上面步骤中除了分解本质矩阵 E E E 外,其他都在之前文章中提到过。分解本质矩阵 E E E 在编程下的代码不难,但是推导过程极其复杂,博主在这里就不叙述了。
import numpy as np # 假设你已经有了一个本质矩阵E
E = np.array([[...], [...], [...]]) # 用你的本质矩阵替换这里的占位符 # 对E进行奇异值分解
U, S, Vt = np.linalg.svd(E) # 根据SVD分解的结果恢复旋转矩阵R和平移向量t
W = np.array([[0, -1, 0], [1, 0, 0], [0, 0, 1]])
R1 = U @ W @ Vt
R2 = U @ W.T @ Vt # 由于t的方向是不确定的,我们通常选择使t的最后一个分量为正的那个解
t1 = U[:, 2]
t2 = -U[:, 2] # 选择合适的R和t组合
if np.linalg.det(R1) * np.linalg.det(np.eye(3) - R1) < 0: R, t = R2, t2
else: R, t = R1, t1 # 现在你有了旋转矩阵R和平移向量t
print("Rotation matrix R:")
print(R)
print("Translation vector t:")
print(t)
2.3 欧式结构恢复歧义
1. 在没有先验信息的情况下,我们求解出来的解跟真实解是存在一个相似变换关系(旋转、平移、缩放)。
2. 度量重构:恢复的场景与真实场景之间仅存在相似变换的重构。如果欧式结构恢复后能达到这种重构的话,那就可以说的上恢复效果是很不错了。


三、仿射结构恢复
3.1 概述
1. 仿射结构恢复问题:摄像机为仿射相机,内外参数均未知。 一般来说仿射相机代表为弱透视投影摄像机。
2. 下面图中所有坐标使用欧式坐标,对于仿射变换而言 z z z 轴的 m 3 X = 1 m_3X=1 m3X=1,所以经过等式变换世界坐标的欧式坐标与像平面欧式坐标关系为 x E = A X E + b x^E=AX^E+b xE=AXE+b。其中 A 2 ∗ 3 , b 2 ∗ 1 A_{2∗3},b_{2∗1} A2∗3,b2∗1。

3. 仿射结构恢复问题可以建模为:已知 n n n 个三维点 X j X_j Xj 在 m m m 张图像中的对应点的像素坐标为 x i j x_{ij} xij,且 x i j = A i X j + b i x_{ij}=A_iX_j+b_i xij=AiXj+bi,其中第 i i i 张图片对应的仿射相机的投影矩阵为 M i M_i Mi。求解 n n n 个三维点 X j X_j Xj 的坐标以及 m m m 个仿射相机的投影矩阵中的 A i A_i Ai, b i b_i bi ( i = 1 , 2 , . . . , m i=1,2,...,m i=1,2,...,m)。

3.2 因式分解法
1. 数据中心化:对于所有像平面点和世界坐标的三维点,分别减去像平面点和三维点的质心,建立新的关系,可知 x ^ i j = A i X ^ j \widehat{x}_{ij}=A_i\widehat{X}_j x ij=AiX j。其中 x ^ i j = x i j − x ˉ i j \widehat{x}_{ij}=x_{ij}-\bar{x}_{ij} x ij=xij−xˉij, X ^ j = X j − X ˉ j \widehat{X}_j=X_j-\bar{X}_j X j=Xj−Xˉj。通过数据中心化消掉了 b b b 的影响。
2. 如果3D点的质心=世界坐标系的中心,那么减去的均值为 0 0 0,所以 x ^ i j = A i X j \widehat{x}_{ij}=A_i{X}_j x ij=AiXj。

3. 矩阵形式如下所示。接下来我们要将 D 2 m ∗ n D_{2m*n} D2m∗n 分解为 M 2 m ∗ 3 M_{2m*3} M2m∗3 和 S 3 ∗ n S_{3*n} S3∗n,即因式分解。


4. 由于 M M M 和 S S S 的秩为 3 3 3,所以 D D D 的秩为 3 3 3,我们对 D 2 m ∗ n D_{2m*n} D2m∗n 矩阵进行奇异值分解。可以得到 D 2 m ∗ n = U 2 m ∗ 3 × W 3 ∗ 3 × V 3 ∗ n D_{2m*n}=U_{2m*3} \times W_{3*3} \times V_{3*n} D2m∗n=U2m∗3×W3∗3×V3∗n。


3.3 总结

3.4 仿射结构恢复歧义
1. 仿射结构恢复歧义:投影矩阵存在一个可逆 3 ∗ 3 3*3 3∗3 矩阵的变换,也就是差了一个仿射变换的矩阵系数。对于歧义我们需要引入其他约束来解决歧义。

2. 另外对于给定 m m m 个相机, n n n 个 3 3 3 维点情况下,我们将有 2 m n 2mn 2mn 个等式, 8 m + 3 n − 8 8m+3n-8 8m+3n−8 个未知量。

相关文章:

计算机视觉之三维重建(6)---多视图几何(上)
文章目录 一、运动恢复结构问题(SfM)二、欧式结构恢复2.1 概述2.2 求解2.3 欧式结构恢复歧义 三、仿射结构恢复3.1 概述3.2 因式分解法3.3 总结3.4 仿射结构恢复歧义 一、运动恢复结构问题(SfM) 1. 运动恢复结构问题:通…...
(栈溢出的处理办法))
蓝桥杯:全球变暖(python,BFS,DFS)(栈溢出的处理办法)
图论的经典题型,深度优先搜索和广度优先搜索都可以,但是本题推荐使用广度优先搜索(类似的题最好都用广度优先搜索),因为使用深度优先搜索会爆栈(栈溢出)。本篇博客两种方法都进行讲解࿰…...

Qt C++ | Qt 元对象系统、信号和槽及事件(第一集)
01 元对象系统 一、元对象系统基本概念 1、Qt 的元对象系统提供的功能有:对象间通信的信号和槽机制、运行时类型信息和动态属性系统等。 2、元对象系统是 Qt 对原有的 C++进行的一些扩展,主要是为实现信号和槽机制而引入的, 信号和槽机制是 Qt 的核心特征。 3、要使用元…...

Python 抽象类
在Python的抽象基类(ABC)中,方法并不是必须全部是抽象方法。抽象基类可以同时包含抽象方法和具体方法。抽象类中可以有抽象方法也可以定义具体方法 具体来说: 抽象方法: 使用abc.abstractmethod装饰器标记的方法是抽象方法。抽象方法没有方法体,只有方法签名。抽象方法必须在具…...
达梦数据库自动备份(全库)+还原(全库) 控制台
一 前提 1.安装达梦数据库DB8(请参照以前文章) 我的数据库安装目录是 /app/dmDB8 2.已创建实例 (请参照上一篇文章) 二 准备测试数据 三 自动备份步骤 1.开启归档模式 开启DM管理工具管理控制台 弹不出来工具的 输入命令 xhost 第一步 将服务器转换为配置状态 右键-&g…...
)
android AndroidAutoSize 取消第三方库适配问题(两个步骤)
比如第三方库的Activity是:PictureSelectorSupporterActivity、PictureSelectorTransparentActivity、CropImageActivity 1.在自定义Application 的 onCreate 方法设置: Overridepublic void onCreate() {super.onCreate();this.mAppthis;registerActi…...
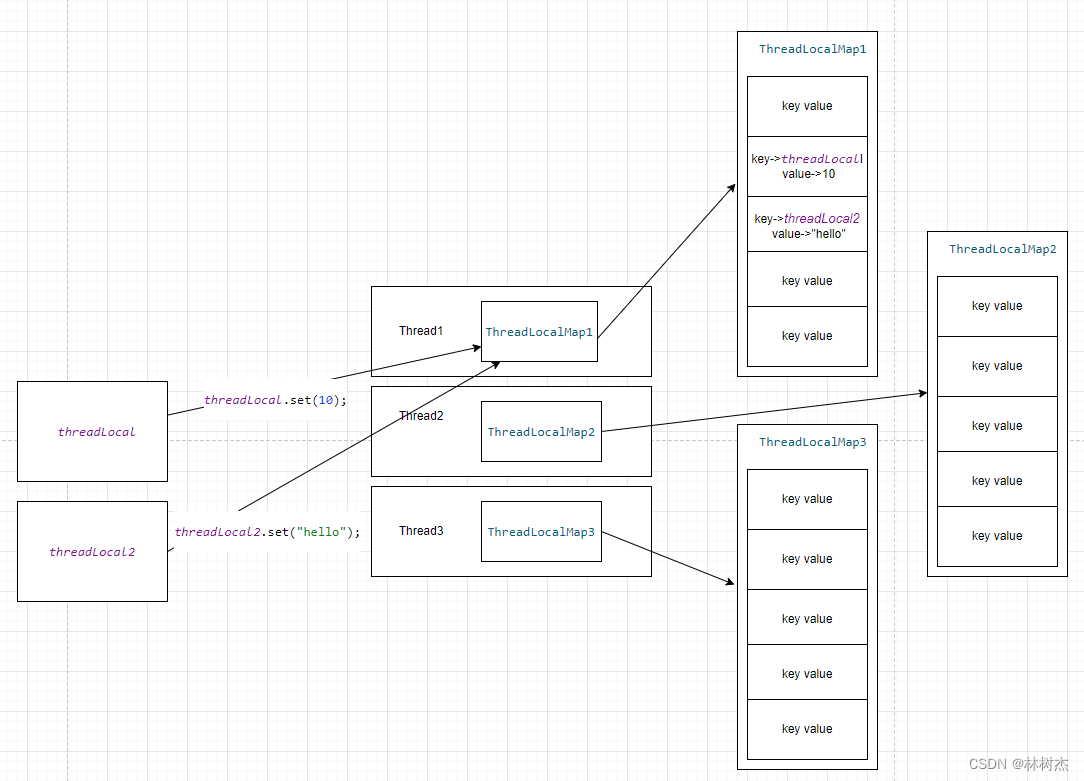
【Java 多线程】从源码出发,剖析Threadlocal的数据结构
文章目录 exampleset(T value)createMap(t, value);set(ThreadLocal<?> key, Object value)ThreadLocalMap和Thread的关系 全貌 ThreadLocal是个很重要的多线程类,里面数据结构的设计很有意思,很巧妙。但是我们平时使用它的时候常常容易对它的使用…...
Sy6 编辑器vi的应用(+shell脚本3例子)
实验环境: 宿主机为win11,网络:10.255.50.5 6389 WSL2 ubuntu 目标机的OS:Ubuntu 内核、版本如下: linuxpeggy0223:/$ uname -r 5.15.146.1-microsoft-standard-WSL2 linuxpeggy0223:/$ cat /proc/version Linux vers…...
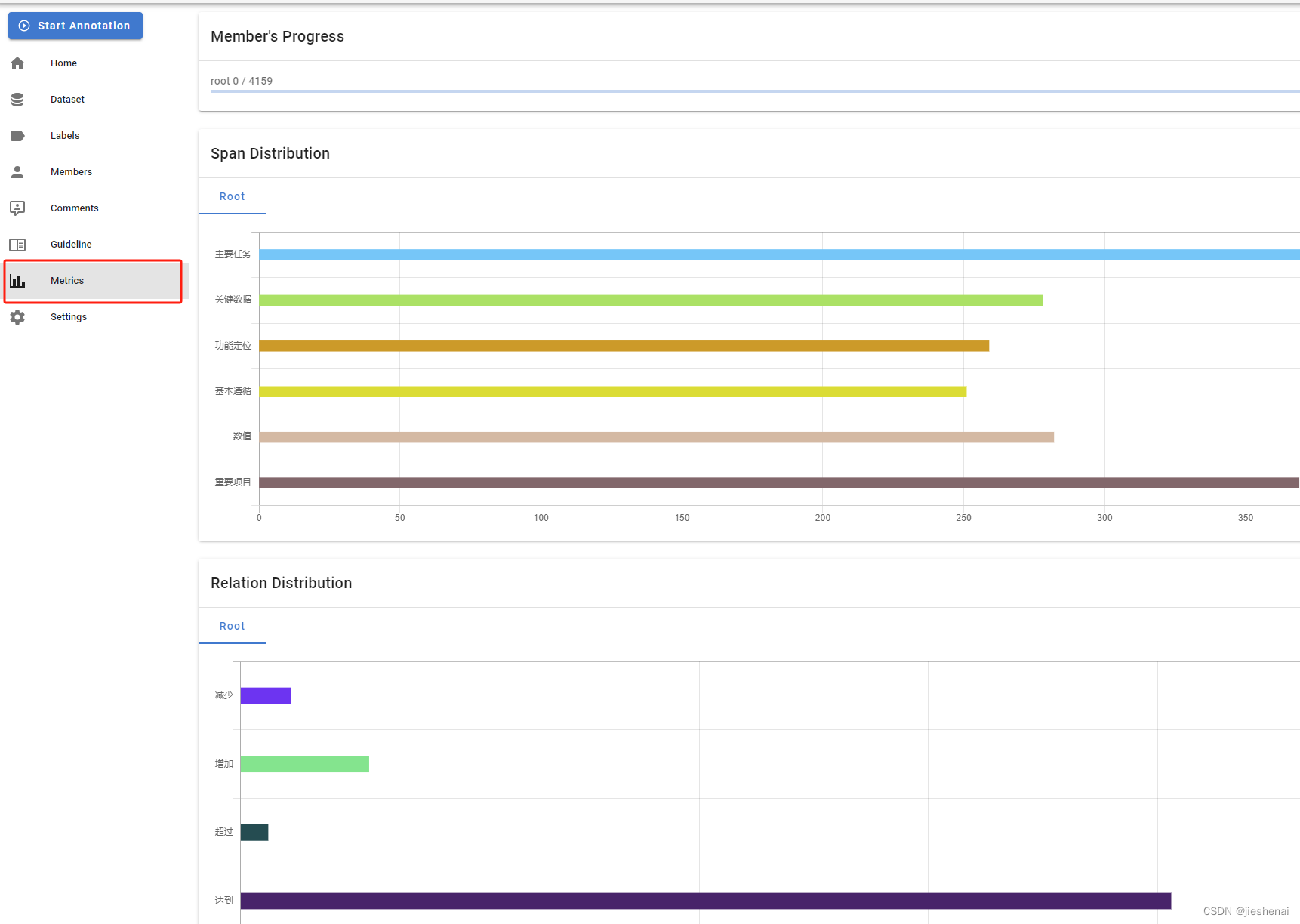
把标注数据导入到知识图谱
文章目录 简介数据导入Doccano标注数据,导入到Neo4j寻求帮助 简介 团队成员使用 Doccano 标注了一些数据,包括 命名实体识别、关系和文本分类 的标注的数据; 工作步骤如下: 首先将标注数据导入到Doccano,查看一下标注…...

【前端基础】什么是类数组对象,类数组对象转换成数组的方法
类数组对象(array-like object)是指在 JavaScript 中具有类似数组的特征但不是真正的数组的对象。这些对象具有类似数组的特性,例如有一个 length 属性和通过索引访问元素的能力,但它们不具备数组对象的所有方法和特性。 什么是类…...
Python快速入门系列-8(Python数据分析与可视化)
第八章:Python数据分析与可视化 8.1 数据处理与清洗8.1.1 数据加载与查看8.1.2 数据清洗与处理8.1.3 数据转换与整理8.2 数据可视化工具介绍8.2.1 Matplotlib8.2.2 Seaborn8.2.3 Plotly8.3 数据挖掘与机器学习简介8.3.1 Scikit-learn8.3.2 TensorFlow总结在本章中,我们将探讨…...

双非硕转测试之Java学习笔记(一):集合
Java学习-----集合 简单概括单列集合--collectionlist接口:vector类:LinkedList类:set接口:HasSet类:LinkedHashSet类: 双列集合--MapMap接口:HashMap类:HashTable类:Pro…...

zabbix源码安装
目录 一.安装php和nginx客户端环境 二.修改php配置 三.修改nginx配置文件 四.下载并编译zabbix 五.创建zabbix需要的用户及组 六.安装编译需要的依赖 七.配置zabbix文件 八.数据库配置 九.配置zabbix 十.web界面部署 十一.遇到无法创建配置文件 十二.登录zabbix 前…...

计算机视觉之三维重建(5)---双目立体视觉
文章目录 一、平行视图1.1 示意图1.2 平行视图的基础矩阵1.3 平行视图的极几何1.4 平行视图的三角测量 二、图像校正三、对应点问题3.1 相关匹配法3.2 归一化相关匹配法3.3 窗口问题3.4 相关法存在的问题3.5 约束问题 一、平行视图 1.1 示意图 如下图即是一个平行视图。特点&a…...

计算机网络-TCP/IP 网络模型
TCP/IP网络模型各层的详细描述: 应用层:应用层为应用程序提供数据传输的服务,负责各种不同应用之间的协议。主要协议包括: HTTP:超文本传输协议,用于从web服务器传输超文本到本地浏览器的传送协议。FTP&…...

算法训练营第29天|LeetCode 491.递增子序列 46.全排列 47.全排列Ⅱ
LeetCode 491.递增子序列 题目链接: LeetCode 491.递增子序列 解题思路: 用哈希集合进行去重,同一树层不能取重复元素。 代码: class Solution { public:vector<vector<int>>result;vector<int>path;void…...

Ubuntu服务器搭建 - 环境篇
Ubuntu服务器搭建 - 环境篇 基于腾讯云服务器 - Ubuntu 20.04 LTS 一、安装 - MySQL 1.1 概述 MySQL安装方式有三种: 1. 使用Ubuntu 包管理工具 apt安装 2. 使用MySQL官方APT存储库安装 3. 使用MySQL官方二进制发行版安装 1.2 安装 MySQL 使用MySQL官方APT存储库安装 $ wget…...

深度学习基础模型之Mamba
Mamba模型简介 问题:许多亚二次时间架构(运行时间复杂度低于O(n^2),但高于O(n)的情况)(例如线性注意力、门控卷积和循环模型以及结构化状态空间模型(SSM))已被开发出来,以解决 Transformer 在长…...

Topaz Video AI for Mac v5.0.0激活版 视频画质增强软件
Topaz Video AI for Mac是一款功能强大的视频处理软件,专为Mac用户设计,旨在通过人工智能技术为视频编辑和增强提供卓越的功能。这款软件利用先进的算法和深度学习技术,能够自动识别和分析视频中的各个元素,并进行智能修复和增强&…...

解决WordPress文章的段落首行自动空两格的问题
写文章时,段落首行都会空两格,可是WordPress自带的编辑器却没有考虑到这一点,导致发布的文章首行都是顶格的,看起来很不习惯。 我们通常的解决方法都是在发布文章时把编辑器切换到“文本”模式,然后再在首行手动键入两…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
)
stm32进入Infinite_Loop原因(因为有系统中断函数未自定义实现)
这是系统中断服务程序的默认处理汇编函数,如果我们没有定义实现某个中断函数,那么当stm32产生了该中断时,就会默认跑这里来了,所以我们打开了什么中断,一定要记得实现对应的系统中断函数,否则会进来一直循环…...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...

手动给中文分词和 直接用神经网络RNN做有什么区别
手动分词和基于神经网络(如 RNN)的自动分词在原理、实现方式和效果上有显著差异,以下是核心对比: 1. 实现原理对比 对比维度手动分词(规则 / 词典驱动)神经网络 RNN 分词(数据驱动)…...
