【蓝桥杯集训16】多源汇求最短路——Floyd算法(2 / 2)
目录
Floyd求最短路模板
4074. 铁路与公路 - floyd + 脑筋急转弯
Floyd求最短路模板
活动 - AcWing
题目:
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,边权可能为负数。
再给定 k 个询问,每个询问包含两个整数 x 和 y,表示查询从点 x 到点 y 的最短距离,如果路径不存在,则输出 impossible
数据保证图中不存在负权回路
public static void floyd(){for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)d[i][j]=Math.min(d[i][j],d[i][k]+d[k][j]);}/**道阻且长,行则将至*author:Roye_ack
*/
import java.util.*;
import java.io.*;
import java.math.*;class Main
{static PrintWriter wt=new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));static int N=210;static int n,m,k;static int[][] d=new int[N][N];public static void floyd(){for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)d[i][j]=Math.min(d[i][j],d[i][k]+d[k][j]);}public static void main(String[] args) throws IOException{n=rd.nextInt();m=rd.nextInt();k=rd.nextInt();for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)if(i==j) d[i][j]=0; //如果是自环else d[i][j]=0x3f3f3f3f;while(m-->0){int a=rd.nextInt(),b=rd.nextInt(),w=rd.nextInt();d[a][b]=Math.min(d[a][b],w); //重边取最小}floyd();while(k-->0){int x=rd.nextInt(),y=rd.nextInt();if(d[x][y]>0x3f3f3f3f/2) wt.println("impossible");else wt.println(d[x][y]);}wt.flush();}static class rd{static BufferedReader bf=new BufferedReader(new InputStreamReader(System.in));static StringTokenizer tk=new StringTokenizer("");static String nextLine() throws IOException{return bf.readLine();}static String next() throws IOException{while(!tk.hasMoreTokens()) tk=new StringTokenizer(bf.readLine());return tk.nextToken();}static int nextInt() throws IOException{return Integer.parseInt(next());}static double nextDouble() throws IOException{return Double.parseDouble(next());}static long nextLong() throws IOException{return Long.parseLong(next());}static BigInteger nextBig() throws IOException{BigInteger d=new BigInteger(rd.nextLine());return d;}}
}class PII
{int x,y;PII(int x,int y){this.x=x;this.y=y;}
}4074. 铁路与公路 - floyd + 脑筋急转弯
4074. 铁路与公路 - AcWing题库
题目:
- 某国家有 n 个城市(编号 1∼n)和 m 条双向铁路
- 对于每对不同的城市 x,y,当且仅当它们之间没有铁路时,它们之间会存在一条双向公路。
- 经过每条铁路或公路都需要花费 1 小时的时间。
- 现在有一列火车和一辆汽车同时离开城市 1,它们的目的地都是城市 n。
- 它们不会在途中停靠(但是可以在城市 n 停靠)。
- 火车只能沿铁路行驶,汽车只能沿公路行驶。
- 请你为它们规划行进路线,每条路线中可重复经过同一条铁路或公路,但是为了避免发生事故,火车和汽车不得同时到达同一个城市(城市 n 除外)。
- 请问,在这些条件的约束下,两辆车全部到达城市 n 所需的最少小时数,即求更慢到达城市 n 的那辆车所需的时间的最小值。
思路:
由题目可知,公路和铁路不会重合
那么必然有一辆车最短时间为1,因为1到n之间必然有一条路(公路或铁路)
一辆车从1直接到n,另一辆走其他路,则两车并不会在中途城市相遇
所以我们直接求两者的最短路即可
由于数据范围较小,我们用floyd算法(O(n^3))
/**道阻且长,行则将至*author:Roye_ack
*/
import java.util.*;
import java.io.*;
import java.math.*;class Main
{static PrintWriter wt=new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));static int N=410;static int n,m;static int[][] tr=new int[N][N];static int[][] car=new int[N][N];public static int floyd(int[][] d){for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++) d[i][j]=Math.min(d[i][j],d[i][k]+d[k][j]);return d[1][n];}public static void main(String[] args) throws IOException{n=rd.nextInt();m=rd.nextInt();for(int i=1;i<=n;i++) Arrays.fill(tr[i],0x3f3f3f3f);for(int i=1;i<=n;i++) Arrays.fill(car[i],0x3f3f3f3f);while(m-->0){int a=rd.nextInt(),b=rd.nextInt();tr[a][b]=tr[b][a]=1;}for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)if(tr[i][j]!=1&&i!=j) car[i][j]=car[j][i]=1;int a=floyd(tr);int b=floyd(car);int res=Math.max(a,b);if(res==0x3f3f3f3f) wt.print(-1);else wt.print(res);wt.flush();}static class rd{static BufferedReader bf=new BufferedReader(new InputStreamReader(System.in));static StringTokenizer tk=new StringTokenizer("");static String nextLine() throws IOException{return bf.readLine();}static String next() throws IOException{while(!tk.hasMoreTokens()) tk=new StringTokenizer(bf.readLine());return tk.nextToken();}static int nextInt() throws IOException{return Integer.parseInt(next());}static double nextDouble() throws IOException{return Double.parseDouble(next());}static long nextLong() throws IOException{return Long.parseLong(next());}static BigInteger nextBig() throws IOException{BigInteger d=new BigInteger(rd.nextLine());return d;}}
}class PII
{int x,y;PII(int x,int y){this.x=x;this.y=y;}
}
相关文章:
)
【蓝桥杯集训16】多源汇求最短路——Floyd算法(2 / 2)
目录 Floyd求最短路模板 4074. 铁路与公路 - floyd 脑筋急转弯 Floyd求最短路模板 活动 - AcWing 题目: 给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,边权可能为负数。 再给定 k 个询问,每个询问包含两个整数 x 和…...

simulink stateflow 状态机
系列文章目录 文章目录系列文章目录前言一、基操二、stateflow 数据三、chart动作四、chart的执行五、flow chart / junction六、状态机中的函数 Stateflow Functions七、chart层次结构八、案例——吸尘器机器人的驱动模式前言 一、基操 在tooltrip中选择DEBUG,通过…...

水库大坝安全监测的主要坝体类型介绍
水电站和水库大坝安全的分类中有重力坝、土石坝等不同的大坝形式。就在这里详细水库大坝安全监测按照建造形式,基本上可以分为三类:重力坝、土石坝和拱坝。 (1)重力坝 重力坝,顾名思义就是利用自身重力来维持坝体稳定…...

物理层概述(二)重点
目录前言编码与调制(1)基带信号与宽带信号编码与调制编码与调制(2)数字数据编码为数字信号非归零编码【NRZ】曼斯特编码差分曼彻斯特编码数字数据调制为模拟信号模拟数据如何编码为数字信号模拟数据调制为模拟信号物理层传输介质导…...
成都待慕电商:抖音极速版商品卡免佣扶持政策规则
新规,抖音极速版推出商品卡免佣扶持政策规则,本次抖音规则如何规定?具体往下看:一、政策简介1.1政策介绍为了更好地满足用户消费需求,丰富商家经营模式,降低商家经营成本,现平台针对商品卡场景推…...

青岛双软认定标准
软件企业的认定是有一定的标准的,需要满足以下这些条件:1、在我国境内依法设立了企业法人的企业;2、以计算机软件开发生产、系统集成、应用服务和其他相应技术服务为经营业务和主要经营收入;3、具有一种以上由本企业开发或由本企业…...

【00后卷王秘籍】python自动化测试—Python自动化框架及工具
1 、概述 手续的关于测试的方法论,都是建立在之前的文章里面提到的观点: 功能测试不建议做自动化 接口测试性价比最高 接口测试可以做自动化 后面所谈到的 测试自动化 也将围绕着 接口自动化 来介绍。 本系列选择的测试语言是 python 脚本语言。由于其…...

MySQL数据库基本操作
DDL 1、DDL解释 DDL(Data Definition Language),数据定义语言,该语言部分包括以下内容: 对数据库的常用操作 对表结构的常用操作 修改表结构1、对数据库的常用操作 2、对表结构的常用操作-创建表 创建表格式 3、对表结构的常用操作-创建表…...

2023年最新的站内SEO指南:如何通过关键词优化提高网站排名
SEO或搜索引擎优化是指通过改善网站的内部和外部元素,以获得更好的自然搜索引擎排名和更多的网站流量。 链接建设和外链是SEO的重要组成部分,因为它们可以提高网站的权威性和可信度,从而使其在搜索引擎中排名更高。 在此指南中,…...

【Java】Java环开发环境安装
Java环开发环境安装 简介: 如果要从事Java编程,则需要安装JDK,如果仅仅是运行一款Java程序则JRE就满足要求。 Java的安装包分为两类 一类是JRE其就是一个独立的Java运行环境; 一类是JDK其是Java的开发环境,不过在JDK…...

[蓝桥杯] 枚举、模拟和排列问题
文章目录 一、连号区间数 1、1 题目描述 1、2 题解关键思路与解答 二、递增三元组 2、1 题目描述 2、2 题解关键思路与解答 三、错误票据 3、1 题目描述 3、2 题解关键思路与解答 四、回文日期 4、1 题目描述 4、2 题解关键思路与解答 五、归并排序 标题:蓝桥杯——…...

C++基础了解-02-C++ 数据类型
C 数据类型 一、C 数据类型 使用编程语言进行编程时,需要用到各种变量来存储各种信息。变量保留的是它所存储的值的内存位置。这意味着,当创建一个变量时,就会在内存中保留一些空间。 可能需要存储各种数据类型(比如字符型、宽…...
关于MSVCR100.dll、MSVCR100d.dll、Msvcp100.dll、abort()R6010等故障模块排查及解决方法
一、常见故障介绍 最近在开发相机项目(项目细节由于公司保密就不介绍了),程序运行5个来月以来首次出现msvcr100.dll故障等问题,于是乎开始了分析之路,按照度娘上的一顿操作,期间也是出现了各种不一样的问…...

【蓝桥杯集训·每日一题】AcWing 3305. 作物杂交
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴Spfa算法一、题目 1、原题链接 3305. 作物杂交 2、题目描述 作物杂交是作物栽培中重要的一步。 已知有 N 种作物 (编号 1 至 N),第 i 种作物从播种到成熟的时间…...

深入浅出PaddlePaddle函数——paddle.to_tensor
分类目录:《深入浅出PaddlePaddle函数》总目录 相关文章: 深入浅出PaddlePaddle函数——paddle.Tensor 深入浅出PaddlePaddle函数——paddle.to_tensor 通过已知的data来创建一个Tensor,Tensor类型为paddle.Tensor。data可以是scalar、tupl…...

JavaScript高级程序设计读书分享之10章——函数
JavaScript高级程序设计(第4版)读书分享笔记记录 适用于刚入门前端的同志 定义函数 定义函数有两种方式:函数声明和函数表达式大致看这两种方式没有什么区别,事实上,JavaScript 引擎在加载数据时对它们是区别对待的。JavaScript 引擎在任何代…...

第八章 使用 ^%ZSTART 和 ^%ZSTOP 例程自定义启动和停止行为 - 设计注意事项
文章目录第八章 使用 ^%ZSTART 和 ^%ZSTOP 例程自定义启动和停止行为 - 设计注意事项设计注意事项第八章 使用 ^%ZSTART 和 ^%ZSTOP 例程自定义启动和停止行为 - 设计注意事项 IRIS 可以在特定事件发生时执行自定义代码。需要两个步骤: 定义 ^%ZSTART 例程、^%ZSTO…...
工作实战之拦截器模式
目录 前言 一、结构中包含的角色 二、拦截器使用 1.拦截器角色 a.自定义拦截器UserValidateInterceptor,UserUpdateInterceptor,UserEditNameInterceptor b.拦截器配置者UserInterceptorChainConfigure,任意组装拦截器顺序 c.拦截器管理者…...
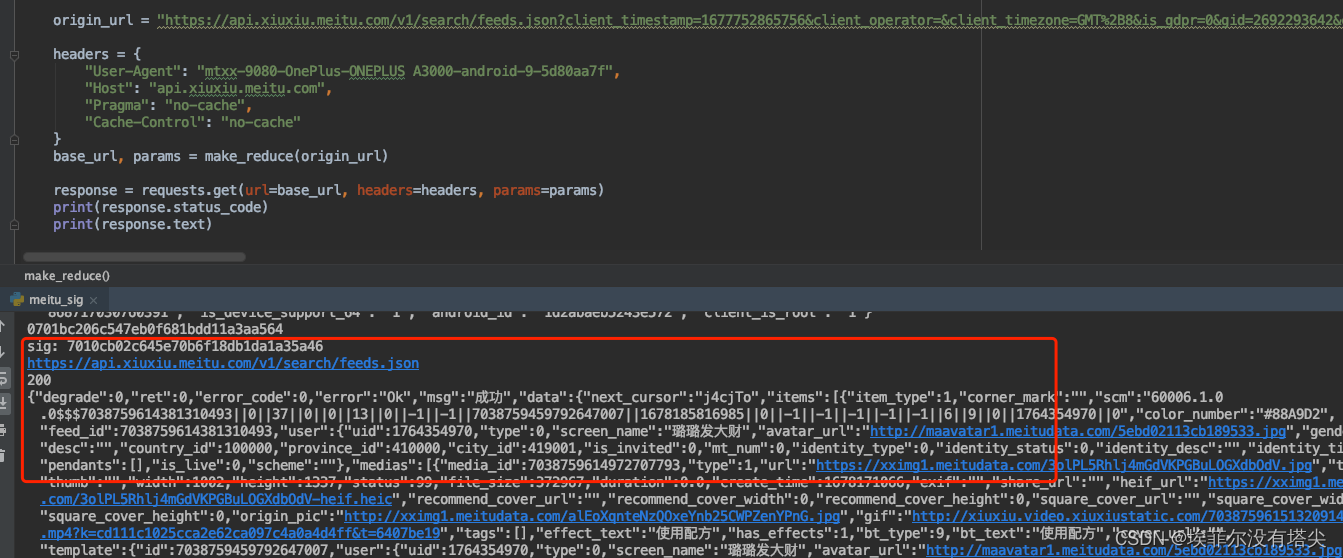
某美颜app sig参数分析
之前转载过该app的文章,今天翻版重新整理下,版本号:576O5Zu56eA56eAYXBwIHY5MDgw (base64 解码)。 上来先抓个包: jadx搜索关键词 "sigTime",然后定位到这里 看这行代码 cVar.addForm(INoCaptchaComponent.sig, genera…...

Linux - Linux系统优化思路
文章目录影响Linux性能的因素CPU内存磁盘I/O性能网络宽带操作系统相关资源系统安装优化内核参数优化文件系统优化应用程序软件资源系统性能分析工具vmstat命令iostat命令sar命令系统性能分析标准小结影响Linux性能的因素 CPU CPU是操作系统稳定运行的根本,CPU的速…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
