Successive Convex Approximation算法的学习笔记
文章目录
- 一、代码debug
- 二、原理
本文主要参考了CSDN上的 另一篇文章,但规范了公式的推导过程和修缮了部分代码
一、代码debug
首先,我们将所有的代码放到MATLAB中,很快在命令行中出现了错误信息

很显然有问题,但是我不知道发生了什么问题。我猜测可能是求解器没有正确安装,因此我正确安装了Gurobi求解器

注意安装Gurobi求解器需要验证license,具体内容可以查询网络上的安装教程。在命令行中输入grbgetkey+licence 就可以完成激活。

但此时还是有问题,我经过查询得知是MEX文件无法指定,是系统路径没有添加gurobi文件的bin,因此我添加到系统路径中


此后文件便可以正确运行了,结果如下。


二、原理
现考虑如下非凸二次规划问题
min f ( x , y ) = [ x , y ] Q [ x , y ] T = x 2 + x y − y 2 s.t. − 1 ≤ x ≤ 1 − 1 ≤ y ≤ 1 \begin{aligned} &\operatorname*{min}f(x,y)&& \left.=\left[\begin{matrix}{x,y}\\\end{matrix}\right.\right]Q\left[\begin{matrix}{x,y}\\\end{matrix}\right]^{T} \\ &&&=x^{2}+xy-y^{2} \\ &\text{s.t.}&& -1\leq x\leq1 \\ &&&-1\leq y\leq1 \end{aligned} minf(x,y)s.t.=[x,y]Q[x,y]T=x2+xy−y2−1≤x≤1−1≤y≤1
其中,
Q = [ 1 0.5 0 5 ] . Q=\begin{bmatrix}1&0.5\\0&5\\\end{bmatrix}. Q=[100.55].
原问题的目标函数可以通过特征值分解转化为凸函数减去凸函数的形式,凸函数减去凸函数未必是凸函数。
Q = V D V T = V ( λ P − λ N ) V T = V λ P V T ⏟ P − V λ N V T ⏟ N \begin{aligned}Q=VDV^T=V\left(\lambda_P-\lambda_N\right)V^T=\underbrace{V\lambda_PV^T}_{P}-\underbrace{V\lambda_NV^T}_{N}\end{aligned} Q=VDVT=V(λP−λN)VT=P VλPVT−N VλNVT
其中,矩阵 P P P 和 N N N 都是半正定矩阵,矩阵 D D D 的表达式如下
D = [ λ 1 λ 2 ⋱ λ k λ k + 1 ⋱ ] = [ λ 1 λ 2 ⋱ λ k 0 ⋱ ] ⏟ λ P − [ 0 0 ⋱ 0 − λ k + 1 ⋱ ] ⏟ λ N D=\left.\left[\begin{array}{cccc}\lambda_{1}& & & & & \\ &\lambda_{2}& & & &\\ & & \ddots & & &\\ & & & \lambda_{k}& &\\ & & & & \lambda_{k+1} &\\ & & & & &\ddots \end{array}\right.\right] =\underbrace{\left.\left[\begin{array}{cccc}\lambda_{1}& & & & & \\ &\lambda_{2}& & & &\\ & & \ddots & & &\\ & & & \lambda_{k}& &\\ & & & & 0 &\\ & & & & &\ddots \end{array}\right.\right]}_{\lambda_P} -\underbrace{\left.\left[\begin{array}{cccc}0& & & & & \\ &0 & & & &\\ & & \ddots & & &\\ & & &0& &\\ & & & & - \lambda_{k+1} &\\ & & & & &\ddots \end{array}\right.\right]}_{\lambda_N} D= λ1λ2⋱λkλk+1⋱ =λP λ1λ2⋱λk0⋱ −λN 00⋱0−λk+1⋱
其中 λ 1 , λ 2 , … , λ k ≥ 0 , λ k + 1 , λ k + 2 , … < 0 \lambda_1,\lambda_2,\ldots,\lambda_k\geq0,\lambda_{k+1},\lambda_{k+2},\ldots<0 λ1,λ2,…,λk≥0,λk+1,λk+2,…<0。
对目标函数的第二项 [ x , y ] N [ x , y ] T \left[x,y\right]N[x,y]^T [x,y]N[x,y]T 在点 ( x ∗ , y ∗ ) (x^{*},y^{*}) (x∗,y∗) 处进行凸近似,即在点 ( x ∗ , y ∗ ) (x^{*},y^{*}) (x∗,y∗) 处进行一阶泰勒展开
− [ x ∗ , y ∗ ] N [ x ∗ , y ∗ ] T − [ ∇ ( [ x , y ] N [ x , y ] T ) ∣ x ∗ , y ∗ ] T ( [ x , y ] − [ x ∗ , y ∗ ] ) T = − [ x ∗ , y ∗ ] N [ x ∗ , y ∗ ] T − ( 2 N [ x ∗ , y ∗ ] T ) T ( [ x , y ] − [ x ∗ , y ∗ ] ) T = − 2 [ x ∗ , y ∗ ] N [ x , y ] T + [ x ∗ , y ∗ ] N [ x ∗ , y ∗ ] T \begin{aligned}&-\left[x^*,y^*\right]N\left[x^*,y^*\right]^T-\left[\nabla\left(\left[x,y\right]N\big[x,y\big]^T\right)\right|_{x^*,y^*}\Big]^T\left(\left[x,y\right]-\left[x^*,y^*\right]\right)^T\\ &=-\left[x^*,y^*\right] N \left[x^*,y^*\right]^T -\left(2N\left[x^*,y^*\right]^T\right)^T\left(\left[x,y\right]-\left[x^*,y^*\right]\right)^T\\ &=-2{\Big[}x^{*},y^{*}{\Big]}N{\Big[}x,y{\Big]}^{T}+{\Big[}x^{*},y^{*}{\Big]}N{\Big[}x^{*},y^{*}{\Big]}^{T} \end{aligned} −[x∗,y∗]N[x∗,y∗]T−[∇([x,y]N[x,y]T) x∗,y∗]T([x,y]−[x∗,y∗])T=−[x∗,y∗]N[x∗,y∗]T−(2N[x∗,y∗]T)T([x,y]−[x∗,y∗])T=−2[x∗,y∗]N[x,y]T+[x∗,y∗]N[x∗,y∗]T
至此,原问题可转化为:
min f ( x , y ) = [ x , y ] P [ x , y ] T − 2 [ x ∗ , y ∗ ] N [ x , y ] T + [ x ∗ , y ∗ ] N [ x ∗ , y ∗ ] T s . t . − 1 ≤ x ≤ 1 − 1 ≤ y ≤ 1 \begin{aligned} &\min & &f\left(x,y\right)=\left[x,y\right]P\left[x,y\right]^{T}-2\left[x^{*},y^{*}\right]N\left[x,y\right]^{T}+\left[x^{*},y^{*}\right]N\left[x^{*},y^{*}\right]^{T} \\ &s.t.& &-1\leq x\leq1 \\ & & &-1\leq y\leq1 \end{aligned} mins.t.f(x,y)=[x,y]P[x,y]T−2[x∗,y∗]N[x,y]T+[x∗,y∗]N[x∗,y∗]T−1≤x≤1−1≤y≤1
clear all
close all
clcQ=[1,0.5;0.5,-1];x=sdpvar(2,1);
xmin=-1;
xmax=1;
Constraints=[];
Constraints=[Constraints,xmin<=x<=xmax];
ops = sdpsettings('solver', 'gurobi', 'verbose', 0);[V,D] = eig(Q);%计算A的特征值对角阵D和特征向量V,使AV=VD成立
lambda_P=D;
lambda_N=-D;
lambda_P(find(D<0))=0;
lambda_N(find(D>0))=0;
P=V*lambda_P*V';
N=V*lambda_N*V';
x0=[0.5;0.5];
x_temp=x0;
while(1)f_k=(x'*P*x-2*x_temp'*N*x+x_temp'*N*x_temp);sol=solvesdp(Constraints,f_k,ops);display([sol.info,' 目标函数值:',num2str(value(x_temp'*Q*x_temp))])x_temp_before=x_temp;x_temp=value(x);if sqrt(sum((x_temp-x_temp_before).^2)/length(x_temp))<1e-10breakend
end
x_result=x_tempX = gridsamp([-1 -1;1 1], 40);
[m,~]=size(X);
YX=zeros(m,1);
for i=1:size(X,1)x=X(i,:);y=x*Q*x';YX(i)=y;
end
X1 = reshape(X(:,1),40,40); X2 = reshape(X(:,2),40,40);
YX = reshape(YX, size(X1));
figure(1), mesh(X1, X2, YX)%绘制预测表面
hold on
scatter3(x_temp(1),x_temp(2),x_temp'*Q*x_temp,200,'r','pentagram','filled')
相关文章:

Successive Convex Approximation算法的学习笔记
文章目录 一、代码debug二、原理 本文主要参考了CSDN上的 另一篇文章,但规范了公式的推导过程和修缮了部分代码 一、代码debug 首先,我们将所有的代码放到MATLAB中,很快在命令行中出现了错误信息 很显然有问题,但是我不知道发生…...

IoT数采平台2:文档
IoT数采平台1:开篇IoT数采平台2:文档IoT数采平台3:功能IoT数采平台4:测试 【平台功能】 基础配置、 实时监控、 规则引擎、 告警列表、 系统配置 消息通知:Websocket 设备上线、设备下线、 数据变化、 告警信息、 实时…...

Vue监听器watch的基本用法
文章目录 1. 作用2. 格式3. 示例3.1 value 值为字符串3.2 value 值为函数3.3 value 值为对象 4. 与计算属性对比 1. 作用 监视数据变化,执行一些业务逻辑或异步操作。 2. 格式 监听器 watch 内部以 key :value 的形式定义,key 是 data 中的…...

MySQL UPDATE JOIN 根据一张表或多表来更新另一张表的数据
当使用MySQL时,经常需要根据一张表或多张表的数据来更新另一张表的数据。这种情况下,我们可以使用UPDATE语句结合JOIN操作来实现这一需求。本文将介绍MySQL中使用UPDATE JOIN的技术。 什么是UPDATE JOIN UPDATE JOIN是MySQL中一种结合UPDATE语句和JOIN…...

JS实现继承的方式ES6版
上一篇:JS实现继承的方式原生版 ES6的继承 主要是依赖extends关键字来实现继承,且继承的效果类似于寄生组合继承。 class Parent() { }class Child extends Parent {constructor(x, y, color) {super(x, y);this.color color;} }子类必须在construct…...
elementui 左侧或水平导航菜单栏与main区域联动
系列文章目录 一、elementui 导航菜单栏和Breadcrumb 面包屑关联 二、elementui 左侧导航菜单栏与main区域联动 三、elementui 中设置图片的高度并支持PC和手机自适应 四、elementui 实现一个固定位置的Pagination(分页)组件 文章目录 系列文章目录…...
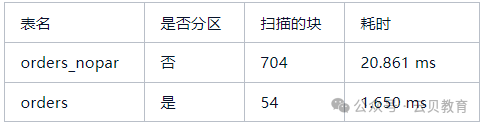
YUNBEE云贝-技术分享:PostgreSQL分区表
引言 PostgreSQL作为一款高度可扩展的企业级关系型数据库管理系统,其内置的分区表功能在处理大规模数据场景中扮演着重要角色。本文将深入探讨PostgreSQL分区表的实现逻辑、详细实验过程,并辅以分区表相关的视图查询、分区表维护及优化案例,…...
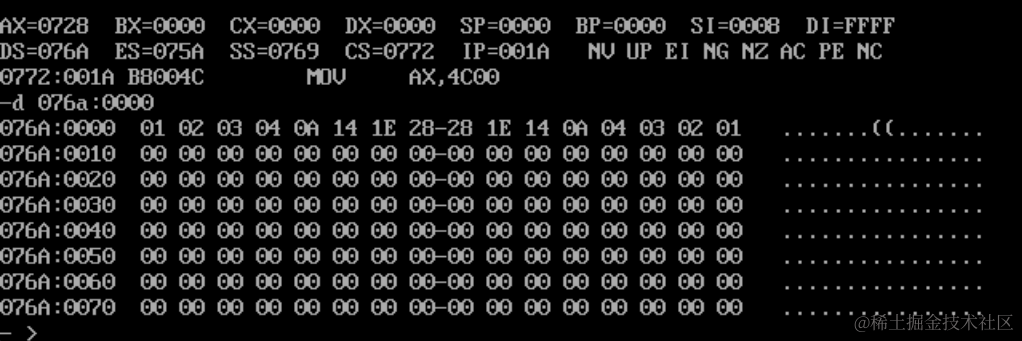
5.2 通用代码,数组求和,拷贝数组,si配合di翻转数组
5.2 通用代码,数组求和,拷贝数组,si配合di翻转数组 1. 通用代码 通用代码类似于一个用汇编语言写程序的一个框架,也类似于c语言的头文件编写 assume cs:code,ds:data,ss:stack data segmentdata endsstack segmentstack endsco…...

Oracle23免费版简易安装攻略
installation-guide 1 安装 root用户下 wget https://yum.oracle.com/repo/OracleLinux/OL8/developer/x86_64/getPackage/oracle-database-preinstall-23c-1.0-1.el8.x86_64.rpm wget https://download.oracle.com/otn-pub/otn_software/db-free/oracle-database-free-23c-1…...

《论文阅读》一种基于反事实推理的会话情绪检测无训练去偏框架 EMNLP 2023
《论文阅读》一种基于反事实推理的会话情绪检测无训练去偏框架 EMNLP 2023 前言简介相关工作模型构架Basic ClassificationBias ExtractionUnbiased Inference实验结果前言 亲身阅读感受分享,细节画图解释,再也不用担心看不懂论文啦~ 无抄袭,无复制,纯手工敲击键盘~ 今天…...

【编译lombok问题】已解决:编译突然找不到符号问题-get/set找不到符号
一、场景:编译突然找不到符号 报错信息: 找不到符号 符号:方法getName() 二、原因: 没有使用lombok支持的编译器 三、解决方法: 打开File-Settings,按以下步骤进行设置; 修改:-Djp…...
第四篇:3.3 无效流量(Invalid traffic) - IAB/MRC及《增强现实广告效果测量指南1.0》
翻译计划 第一篇概述—IAB与MRC及《增强现实广告效果测量指南》之目录、适用范围及术语第二篇广告效果测量定义和其他矩阵之- 3.1 广告印象(AD Impression)第三篇广告效果测量定义和其他矩阵之- 3.2 可见性 (Viewability)第四篇广…...

PyTorch示例——使用Transformer写古诗
文章目录 PyTorch示例——使用Transformer写古诗1. 前言2. 版本信息3. 导包4. 数据与预处理数据下载先看一下原始数据开始处理数据,过滤掉异常数据定义 词典编码器 Tokenizer定义数据集类 MyDataset测试一下MyDataset、Tokenizer、DataLoader 5. 构建模型位置编码器…...
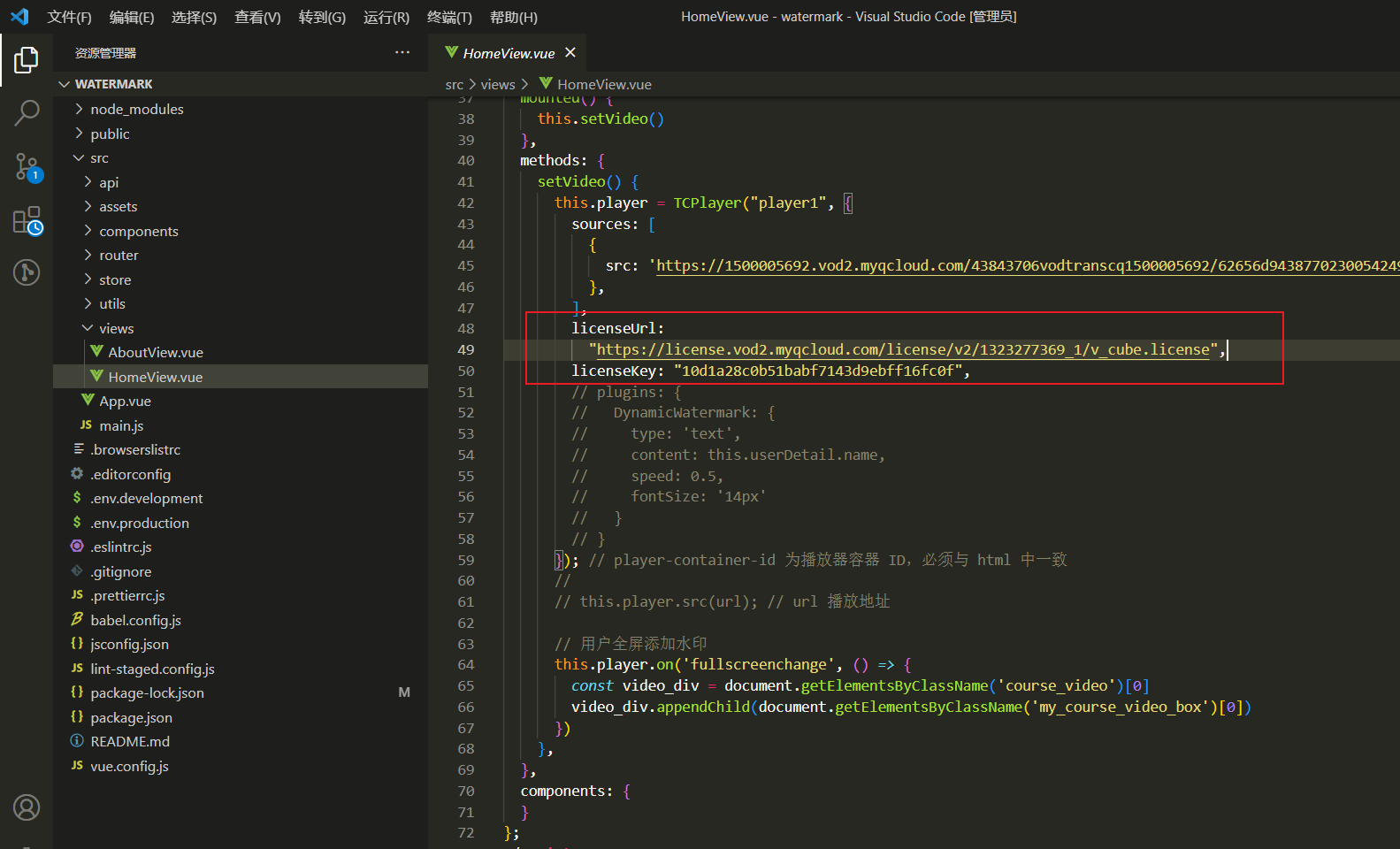
vue 视频添加水印
1.需求背景 其实腾讯云点播的api也支持视频水印,但是只有单个水印,大概效果是这样子的,不满足我们的需求,我们的需求是需要视频中都是水印。 腾讯云点播水印 项目需求的水印(主要是防录屏,最后的实现效果是这样&…...
Web Animations API 动画
Element.animate() dom.animate动画可以避免污染dom原有的css动画 参考资料 Element.animate() - Web API 接口参考 | MDN Element: getAnimations() method - Web APIs | MDN .tunnel{width:200px;height:200px;background-color:#38f;}<div class"tunnel" …...
【大数据存储】实验五:Mapreduce
实验Mapreduce实例——排序(补充程序) 实验环境 Linux Ubuntu 16.04 jdk-8u191-linux-x64 hadoop-3.0.0 hadoop-eclipse-plugin-2.7.3.jar eclipse-java-juno-SR2-linux-gtk-x86_64 实验内容 在电商网站上,当我们进入某电商页面里浏览…...

日志服务 HarmonyOS NEXT 日志采集最佳实践
作者:高玉龙(元泊) 背景信息 随着数字化新时代的全面展开以及 5G 与物联网(IoT)技术的迅速普及,操作系统正面临前所未有的变革需求。在这个背景下,华为公司自主研发的鸿蒙操作系统(…...
 (C dp D前缀和优化倍数关系dp))
Educational Codeforces Round 133 (Rated for Div. 2) (C dp D前缀和优化倍数关系dp)
A:能用3肯定用三,然后分类讨论即可 #include<bits/stdc.h> using namespace std; const int N 2e510,M2*N,mod998244353; #define int long long typedef long long LL; typedef pair<int, int> PII; typedef unsigned long long ULL; usi…...

【讲解下如何Stable Diffusion本地部署】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

算法刷题-回溯
今天给大家分享的还是一道关于dfs回溯的问题,对于这类问题大家还是要多刷和总结,总体难度还是偏大。 对于回溯问题有几个关键点: 1.首先对于这类回溯可以节点可以随机选择的问题,要做mian函数中循环调用dfs(i&#x…...
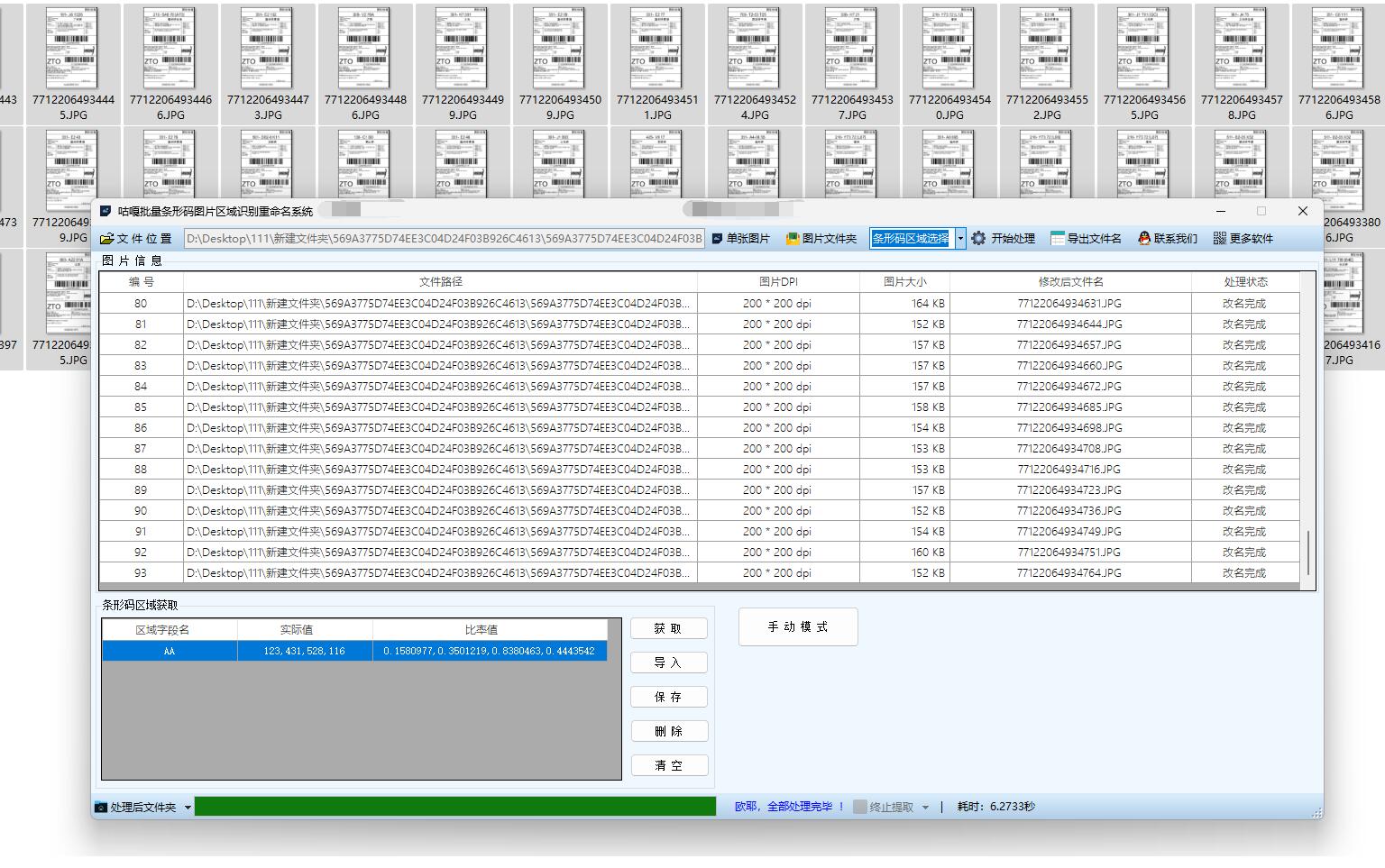
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...

vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能
vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能 查看官网:https://vxetable.cn 效果 代码 通过 checkbox-config.isShift 启用批量选中,启用后按住快捷键和鼠标批量选取 <template><div><vxe-grid v-bind"gri…...