Stable Diffusion扩散模型【详解】小白也能看懂!!
文章目录
- 1、Diffusion的整体过程
- 2、加噪过程
- 2.1 加噪的具体细节
- 2.2 加噪过程的公式推导
- 3、去噪过程
- 3.1 图像概率分布
- 4、损失函数
- 5、 伪代码过程
此文涉及公式推导,需要参考这篇文章: Stable Diffusion扩散模型推导公式的基础知识
1、Diffusion的整体过程
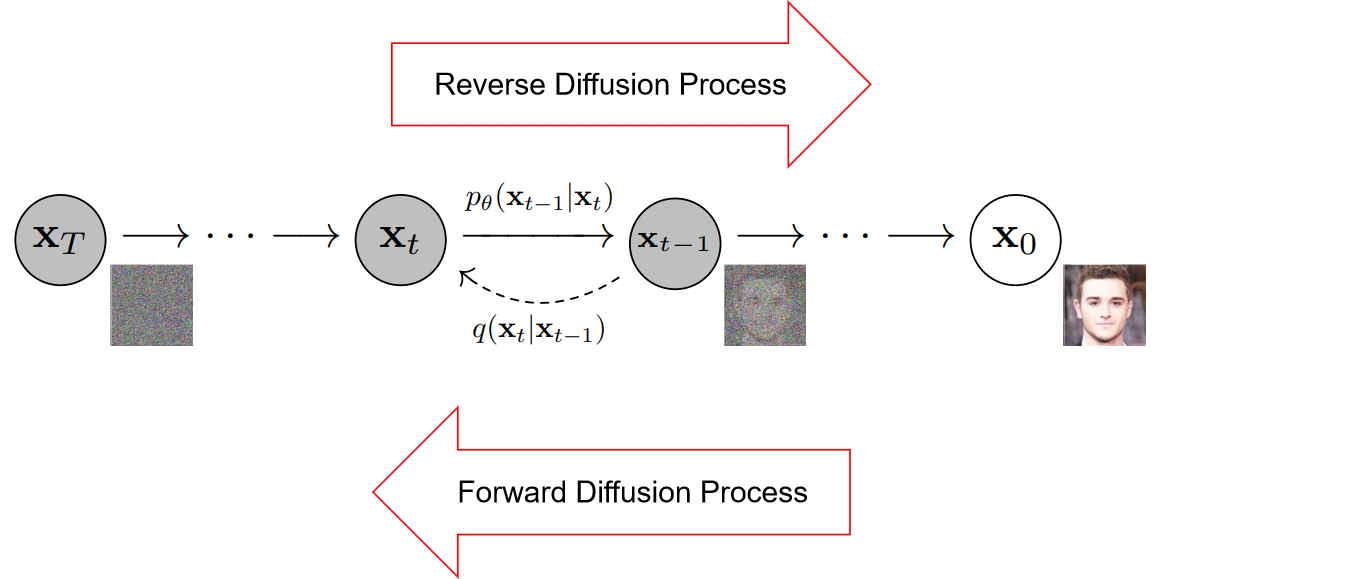
扩散过程是模拟图像加噪的逆向过程,也就是实现去噪的过程,
加噪是如下图从右到左的过程,称为反向扩散过程,
去噪是从左往右的过程,称为前向扩散过程,
2、加噪过程
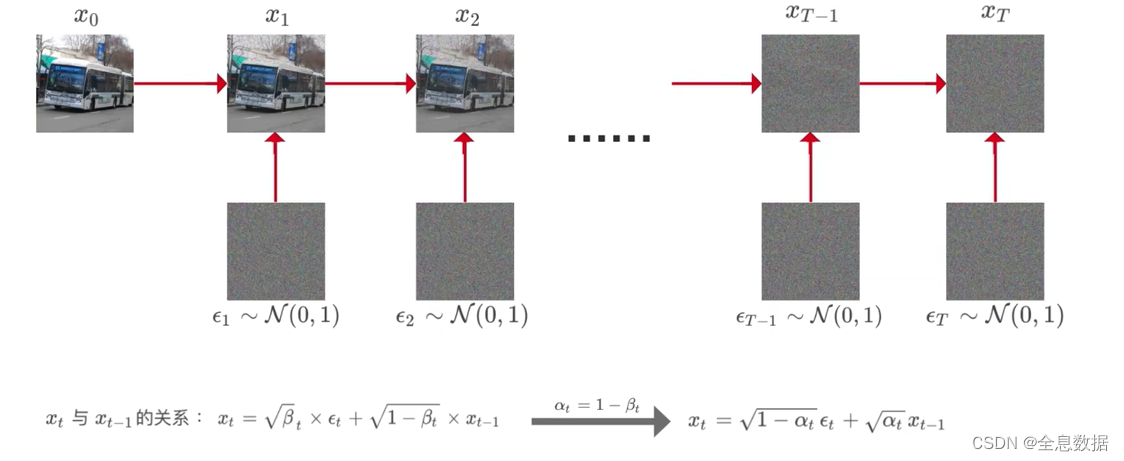
加噪过程如下图,下一时刻的图像是在上一时刻图像的基础上加入噪音生成的,
图中公式的含义: x t x_t xt表示 t 时刻的图像, ϵ t \epsilon_t ϵt 表示 t 时刻生成的随机分布的噪声图像, β t \beta_t βt表示 t 时刻指定的常数,不同时刻的 β t \beta_t βt不同,随着时间 t 的递增而增加,但需要注意 β t \beta_t βt的值始终是比较小的,因为要让图像的数值占较大的比例,
2.1 加噪的具体细节
A、将图像 x x x像素值映射到[-1,1]之间
图像加噪不是在原有图像上进行加噪的,而是通过把图片的每个像素的值转换为-1到1之间,比如像素的值是 x x x,则需要经过下面公式的处理 x 255 × 2 − 1 \frac{x}{255}\times2-1 255x×2−1,转换到范围是-1到1之间,
代码:
def get_transform():class RescaleChannels(object):def __call__(self, sample):return 2 * sample - 1return torchvision.transforms.Compose([torchvision.transforms.ToTensor(), RescaleChannels()])
B、生成一张尺寸相同的噪声图片,像素值服从标准正态分布
ϵ ∼ N ( 0 , 1 ) \epsilon \sim N(0,1) ϵ∼N(0,1)
x = {Tensor:(2, 3, 32, 32)}
noise = torch.randn_like(x)
C、 α \alpha α和 β \beta β
每个时刻的 β t \beta_t βt都各不相同,0 < β t \beta_t βt< 1,因为 β t \beta_t βt是作为权重存在的,且 β 1 < β 2 < β 3 < β T − 1 < β T \beta_1< \beta_2< \beta_3< \beta_{T-1}< \beta_T β1<β2<β3<βT−1<βT,
代码:
betas = generate_linear_schedule(args.num_timesteps,args.schedule_low * 1000 / args.num_timesteps,args.schedule_high * 1000 / args.num_timesteps)
β \beta β的取值代码,比如 β 1 \beta_1 β1取值low, β T \beta_T βT取值high,
# T:1000 Low/β1: 0.0001 high/βT: 0.02
def generate_linear_schedule(T, low, high):return np.linspace(low, high, T)
α t = 1 − β t \alpha_t=1-\beta_t αt=1−βt,alphas = 1.0 - betas
alphas = 1.0 - betas
alphas_cumprod = np.cumprod(alphas)
to_torch = partial(torch.tensor, dtype=torch.float32)
self.registerbuffer("betas", totorch(betas))
self.registerbuffer("alphas", totorch(alphas))
self.register_buffer("alphas_cumprod", to_torch(alphas_cumprod))
self.register_buffer("sqrt_alphas_cumpnod", to_torch(np.sqrt(alphas_cumprod)))
self.register_buffer("sart_one_minus_alphas_cumprod", to_torch(np.sqrt(1 - alphas_cumprod)))
self.registerbuffer("reciprocal sart_alphas", totorch(np.sart(1 / alphas)))
self.register_buffer("remove_noise_coeff", to_torch(betas / np.sqrt(1 - alphas_cumprod)))
self.registerbuffer("siqma",to_torch(np.sqrt(betas)))
D、任一时刻的图像 x t x_t xt都可以由原图像 x 0 x_0 x0直接生成(可以由含 x 0 x_0 x0的公式直接表示)
x t x_t xt与 x 0 x_0 x0的关系: x t = 1 − α t ‾ ϵ + α t ‾ x 0 x_t=\sqrt{1-\overline{\alpha_t}}\epsilon+\sqrt{\overline{\alpha_t}}x_0 xt=1−αtϵ+αtx0, α t = 1 − β t \alpha_t=1-\beta_t αt=1−βt, α t ‾ = α t α t − 1 . . . α 2 α 1 \overline{\alpha_t}=\alpha_t\alpha_{t-1}...\alpha_2\alpha_1 αt=αtαt−1...α2α1
由上式可知, β t \beta_t βt是常数,则 α t \alpha_t αt, 1 − α t ‾ \sqrt{1-\overline{\alpha_t}} 1−αt, α t ‾ \sqrt{\overline{\alpha_t}} αt也是常数, ϵ \epsilon ϵ也是已知的,所以可以直接由 x 0 x_0 x0生成 x t x_t xt,
def perturb_x(self, x, t, noise):return (extract(self.sqrt_alphas_cumprod, t, x.shape) * x +extract(self.sqrt_one_minus_alphas_cumprod, t, x.shape) * noise)
def extract(a, t, x_shape):b, *_ = t.shapeout = a.gather(-1, t)return out.reshape(b, *((1,) * (len(x_shape) - 1)))
2.2 加噪过程的公式推导
加噪过程:
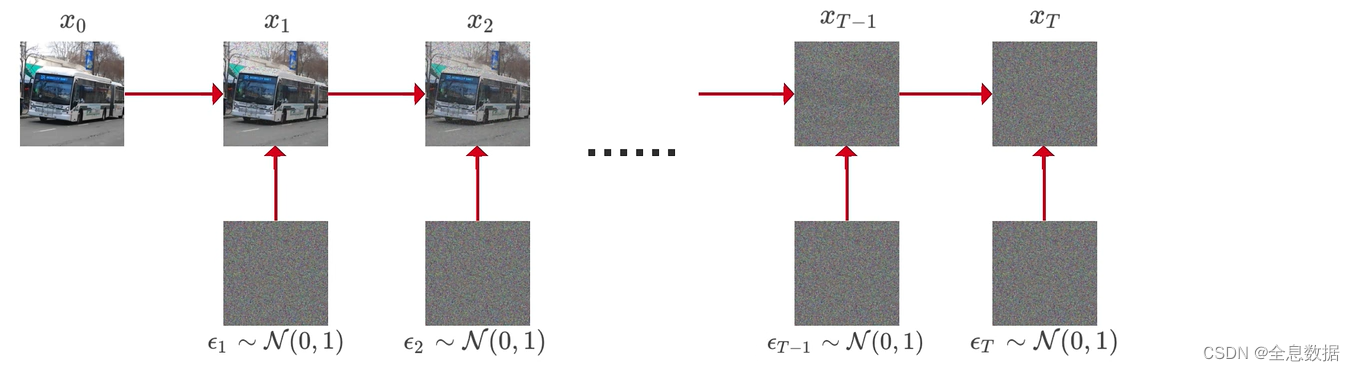
加噪过程的公式:




总结:

3、去噪过程
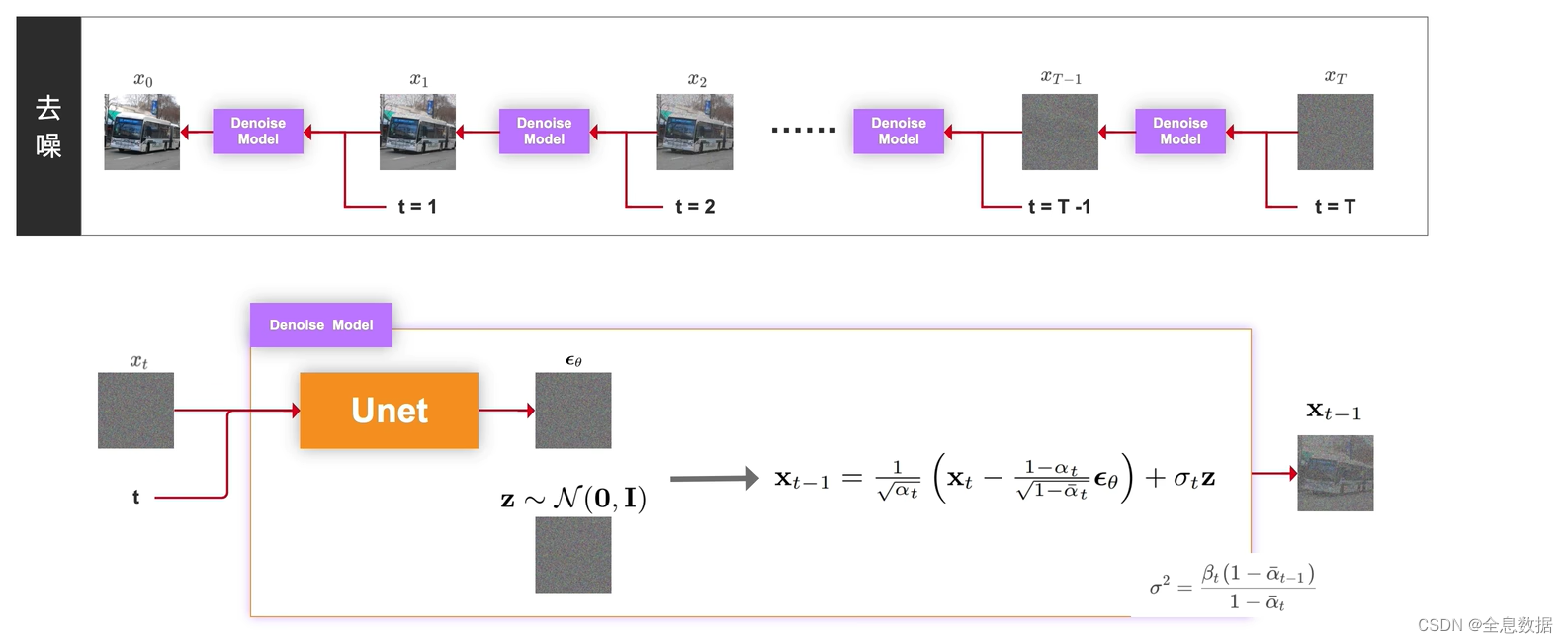
去噪是加噪的逆过程,由时间T时刻的图像逐渐去噪到时刻为0的图像,
下面介绍一下由时刻为T的图像 x T x_T xT去噪到时刻为T-1的图像 x T − 1 x_{T-1} xT−1,输入为时刻为t的图像 x t x_t xt和时刻t,喂给Unet网络生成 ϵ θ \epsilon_\theta ϵθ,其中 θ \theta θ是Unet网络的所有参数,然后由下图中的 x t − 1 {\bf x}_{t-1} xt−1的公式即可生成时刻为t-1的图像 x t − 1 {\bf x}_{t-1} xt−1,
3.1 图像概率分布
去噪过程的2个假设:
(1)加噪过程看作马尔可夫链,假设去噪过程也是马尔可夫链,
(2)假设去噪过程是高斯分布,

假设数据集中有100张图片,每张图片的shape是4x4x3,假设每张图片的每个channel的每个像素点都服从正态分布, x t − 1 x_{t-1} xt−1的正态分布的均值 μ \mu μ 和方差 σ 2 \sigma^2 σ2 只和 x t x_t xt有关,已知在t时刻的图像,求t-1时刻的图像,

1、因为均值和方差 μ ( x t ) \mu(x_t) μ(xt), σ 2 ( x t ) \sigma^2(x_t) σ2(xt) 无法求出,所以我们决定让网络来帮我们预测均值和方差,
2、因为每一个像素都有自己的分布,都要预测出一个均值和方差,所以网络输出的尺寸需要和图像尺寸一致,所以我们选用 Unet 网络,
3、作者在论文中表示,方差并不会影响结果,所以网络只要预测均值就可以了,
4、损失函数

我们要求极大似然的最大值,需要对 μ \mu μ和 σ \sigma σ求导,但是对于扩散的过程是不可行的,如下面的公式无法求出,因为 x 1 : x T x_1:x_T x1:xT的不同组合所求出的 x 0 x_0 x0的值也不同,
p ( x 0 ) = ∫ x 1 : x T p ( x 0 ∣ x 1 : x T ) d x 1 : x T p(x_0)=\int_{x_1:x_T}p(x_0|x_1:x_T)d_{x_1:x_T} p(x0)=∫x1:xTp(x0∣x1:xT)dx1:xT
为了实现对极大似然函数的求导,把对极大似然求导的问题转换为ELBO :Evidence Lower Bound

对ELBO的公式继续进行化简,
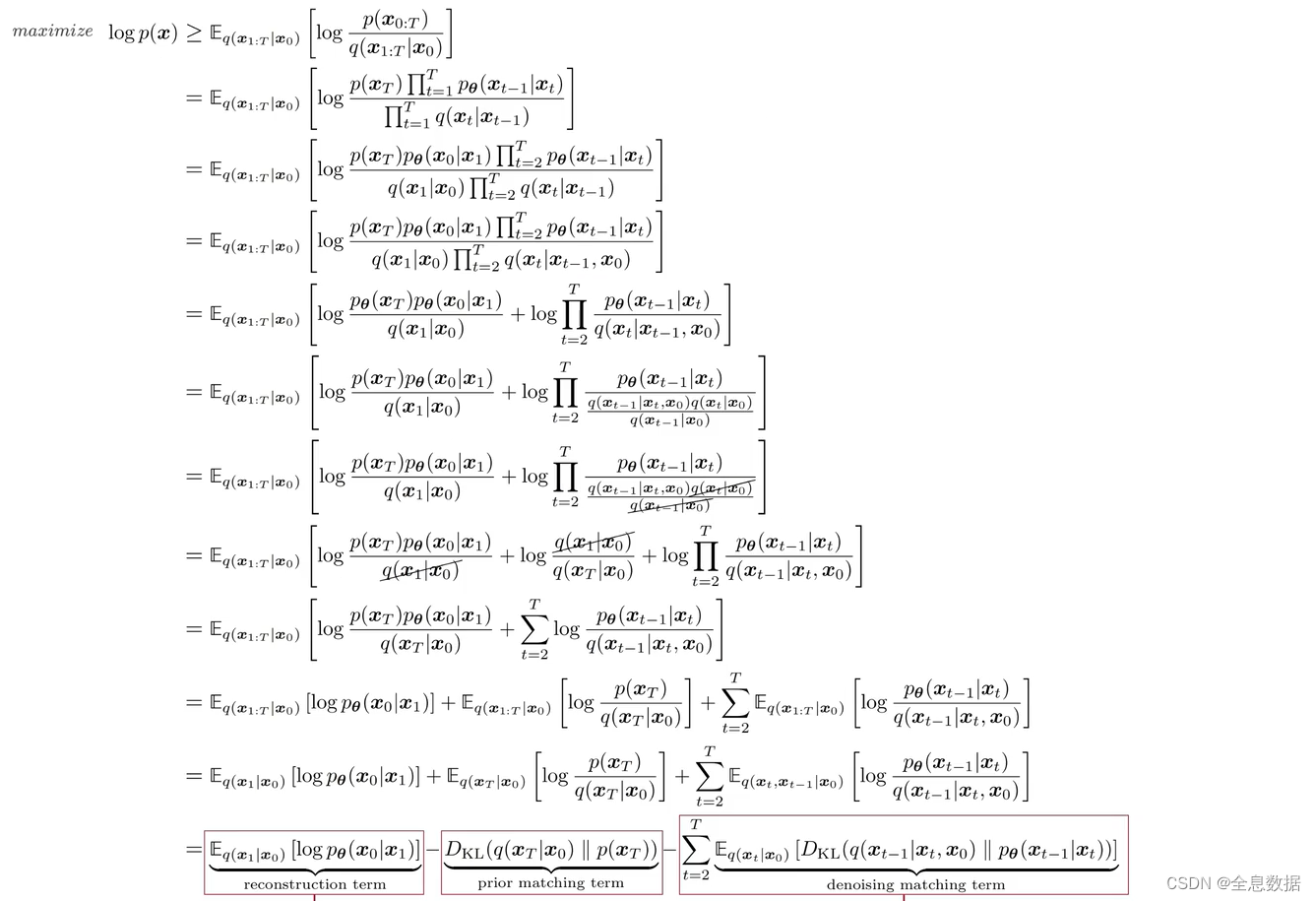

首先来看 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)表示已知 x 0 x_0 x0和 x t x_t xt的情况下推导 x t − 1 x_{t-1} xt−1,这个公式是可以求解的,如上图公式推导; p θ ( x t − 1 ∣ x t ) p_{\theta}(x_{t-1}|x_t) pθ(xt−1∣xt)需要使用 Unet 预测出该分布的均值,
q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)公式的推导如下:

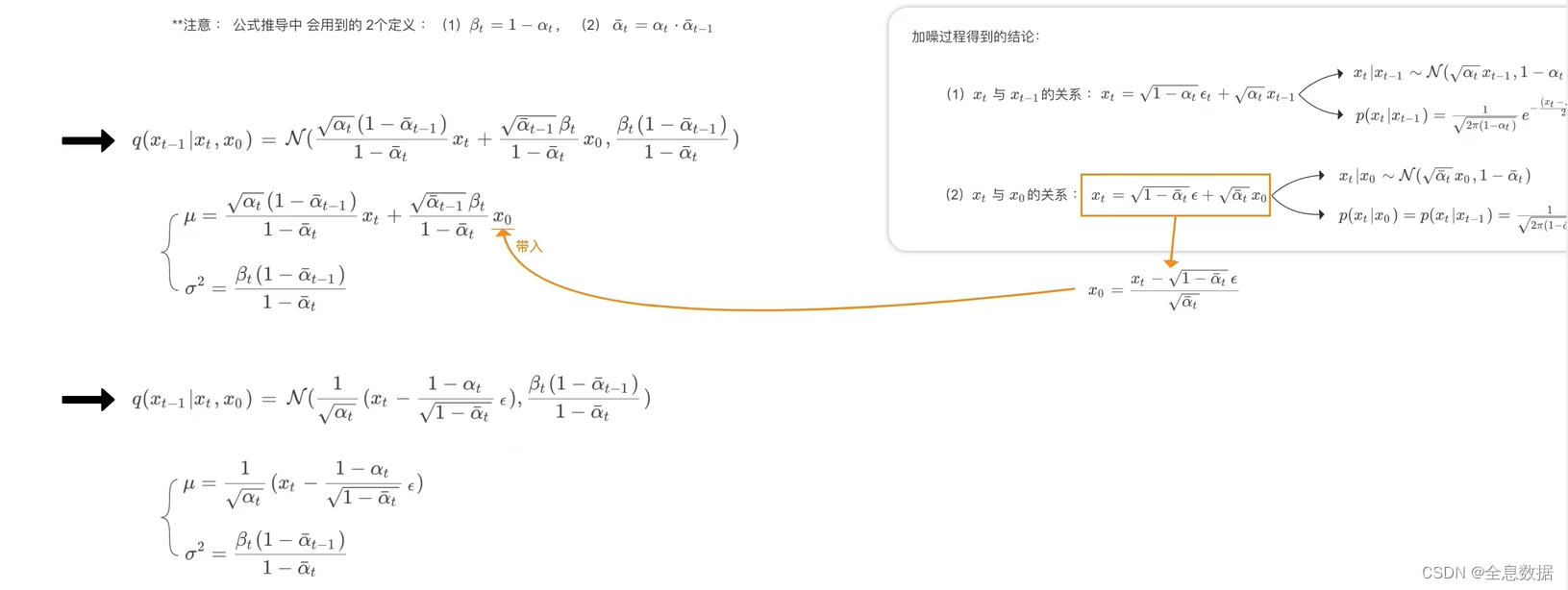
综上可知,UNet是在预测下面的公式,下面的公式中除了 ϵ \epsilon ϵ之外都是已知量,所以UNet网络实际预测的就是 ϵ \epsilon ϵ,
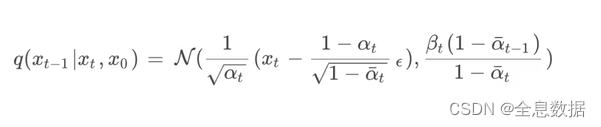
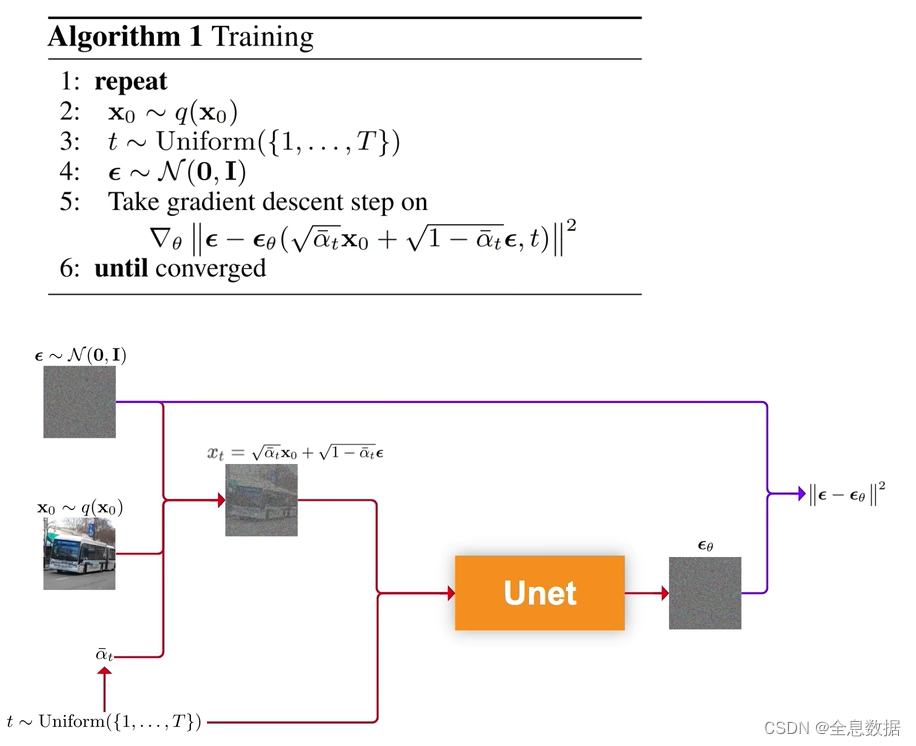
5、 伪代码过程
下图是训练阶段的伪代码,第1行和第6行表示第2行到第5行的代码一直在循环,
第2行:从数据集中筛选出一张图像,即为 x 0 \bf{x}_0 x0,
第3行:从0到 T T T的均匀分布中筛选出 t t t,源码中 T T T的范围设为1000,
第4行:从均值为0,方差为1的标准正态分布中采样出 ϵ \epsilon ϵ, ϵ \epsilon ϵ的size和 x 0 \bf{x}_0 x0的size是相同的,
第5行: x t x_t xt和从0到 T T T的均匀分布中筛选出 t t t喂给Unet,输出 ϵ θ \epsilon_\theta ϵθ,和第4行代码采样出的 ϵ \epsilon ϵ, ∣ ∣ ϵ − ϵ θ ( . . . ) ∣ ∣ 2 ||\epsilon-\epsilon_\theta(...)||^2 ∣∣ϵ−ϵθ(...)∣∣2的均方差作为损失函数,对这个损失函数求梯度进行参数更新,参数是Unet所有参数的集合 θ \theta θ,
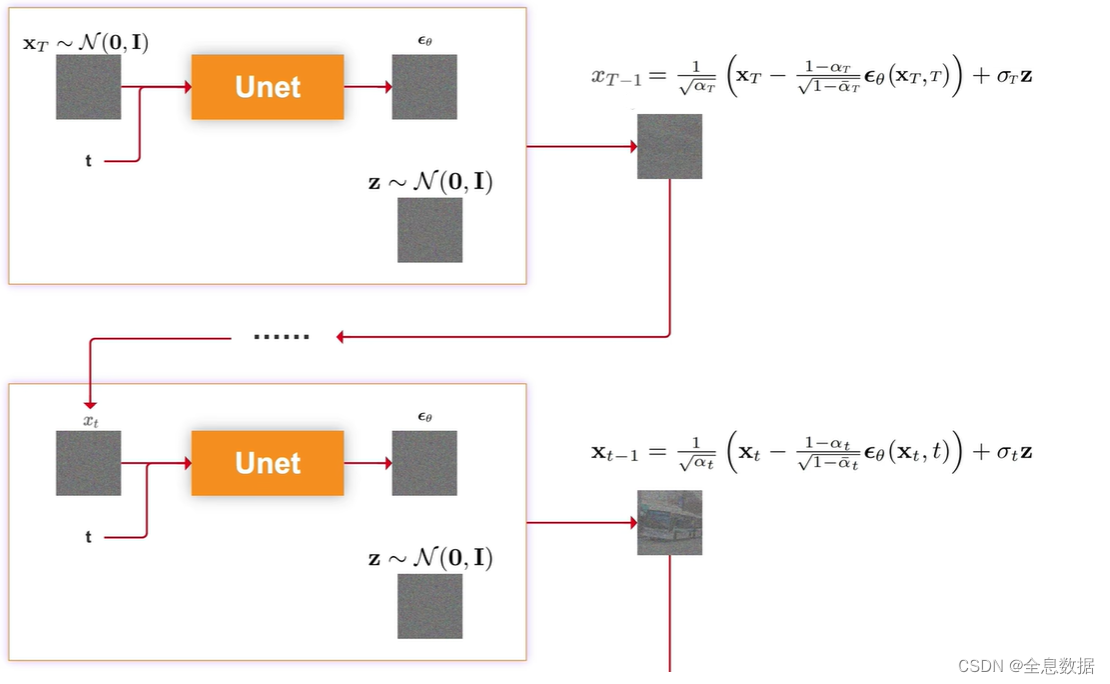
下图是推导/采样/生成图片阶段的伪代码,
第1行:从随机分布中采样一个 x T {\bf x}_T xT,
第2行:遍历从 T T T到1,
第3行:从随机分布中采样一个 z \bf{z} z,
第4行:已知 z \bf{z} z、 α t \alpha_t αt、 σ t \sigma_t σt, ϵ θ \epsilon_\theta ϵθ是Unet网络生成的,就可以得到 x t − 1 {\bf x}_{t-1} xt−1
循环2-4行代码,

参考:
1、CSDN链接:链接
2、哔哩视频:https://www.bilibili.com/video/BV1ju4y1x7L4/?p=5&spm_id_from=pageDriver
3、论文Denoising Diffusion Probabilistic Models:https://arxiv.org/pdf/2006.11239.pdf
相关文章:

Stable Diffusion扩散模型【详解】小白也能看懂!!
文章目录 1、Diffusion的整体过程2、加噪过程2.1 加噪的具体细节2.2 加噪过程的公式推导 3、去噪过程3.1 图像概率分布 4、损失函数5、 伪代码过程 此文涉及公式推导,需要参考这篇文章: Stable Diffusion扩散模型推导公式的基础知识 1、Diffusion的整体…...

关于rabbitmq的prefetch机制
消息预取机制(Prefetch Mechanism)是RabbitMQ中用于控制消息传递给消费者的一种机制。它定义了在一个信道上,消费者允许的最大未确认的消息数量。一旦未确认的消息数量达到了设置的预取值,RabbitMQ就会停止向该消费者发送更多消息…...

机器学习介绍
机器学习是人工智能(AI)的一个分支,它使计算机系统能够从数据中学习并改进它们的性能。机器学习的核心在于开发算法,这些算法可以从大量数据中识别模式和特征,并用这些信息来做出预测或决策,而无需进行明确…...
OpenCV4.9开发之Window开发环境搭建
1.打开OpenCV所在github地址 2.点击opencv仓库,进入仓库详情,点击右下方的OpenCV 4.9.0进入下载页面 3.点击opencv-4.9.0-windows.exe下载 开始下载中... 下载完成 下载完成后,双击运行解压,默认解压路径,修改为c:/...

DDD 中的实体和值对象有什么区别?
在DDD中,实体 Entity 和值对象 Value Object 是两个基本的概念,它们之间有一些重要的区别。 唯一性:实体是唯一的,每个实体都有一个唯一的标识符,即使它的属性在一段时间内发生了变化,它仍然是这个实体。与…...

算法-最值问题
#include<iostream> using namespace std; int main() {int a[7];//上午上课时间int b[7];//下午上课时间int c[7];//一天总上课时间for (int i 0; i < 7; i) {cin >> a[i] >> b[i];c[i] a[i] b[i];}int max c[0];//max记录最长时间int index -1;//索…...

Go 性能压测工具之wrk介绍与使用
在项目正式上线之前,我们通常需要通过压测来评估当前系统能够支撑的请求量、排查可能存在的隐藏bug;压力测试(压测)是确保系统在高负载情况下仍能稳定运行的重要步骤。通过模拟高并发场景,可以评估系统的性能瓶颈、可靠…...
)
数学思想论(有目录)
数学思想是数学发展过程中的重要指导原则,它涉及对数学概念、方法和理论的理解和认识,以及如何利用这些工具来解决实际问题。数学思想的形成和演进是随着数学的发展而逐渐深化的,它体现了人类对数学本质和应用的不断探索和思考。 一些主要的数学思想包括: 函数与方程思想…...
C++的并发世界(五)——线程状态切换
0.线程状态 初始化:该线程正在被创建; 就绪:该线程在列表中就绪,等待CPU调度; 运行:该线程正在运行; 阻塞:该线程被阻塞挂机,Blocked状态包括:pendÿ…...
C语言——指针
地址是由物理的电线上产生的,能够标识唯一一个内存单元。在C语言中,地址也叫做指针。 在32位机器中,有32根地址线。地址是由32个0/1组成的二进制序列,也就是用4个字节来存储地址。 在64位机器中,有64根地址线。地址是…...

手搓二分查找
第一种: 该种方法是若a[mid]目标数,则让r一直等于mid,让l往右移动,一直移动到rl,这时候跳出循环,在循环外判断 但是不能写成让lmid,让r往左移动,比如a[2]key,这时&#x…...

pycharm调试(步过(Step Over)、单步执行(Step Into)、步入(Step Into)、步出(Step Out))
pycharm调试 pycharm调试 pycharm调试为什么要学会调试?1. 步过 (Step Over)2. 单步执行 (Step Into)3. 步入(Step Into)4. 步出(Step Out) 为什么要学会调试? 调试可以帮助初学者更深入地理解编程基础&am…...
Linux是什么,该如何学习
🐇明明跟你说过:个人主页 🏅个人专栏:《Linux :从菜鸟到飞鸟的逆袭》 🏅 🔖行路有良友,便是天堂🔖 目录 一、引言 1、Linux的起源与发展 2、Linux在现代计算机领域…...

C++ | Leetcode C++题解之第7题整数反转
题目: 题解: class Solution { public:int reverse(int x) {int rev 0;while (x ! 0) {if (rev < INT_MIN / 10 || rev > INT_MAX / 10) {return 0;}int digit x % 10;x / 10;rev rev * 10 digit;}return rev;} };...
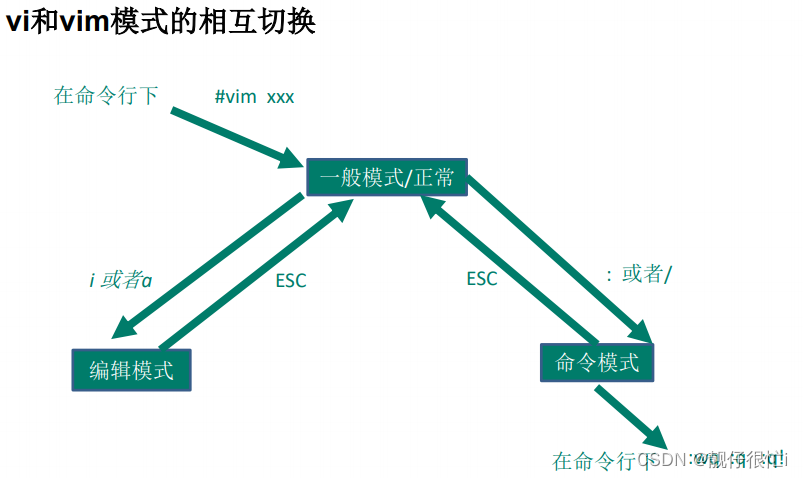
Linux------一篇博客了解Linux最常用的指令
🎈个人主页:靓仔很忙i 💻B 站主页:👉B站👈 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:Linux 🤝希望本文对您有所裨益,如有不足之处&#…...
vscode安装通义灵码
作为vscode的插件,直接使用 通义灵码-灵动指间,快码加编,你的智能编码助手 通义灵码,是一款基于通义大模型的智能编码辅助工具,提供行级/函数级实时续写、自然语言生成代码、单元测试生成、代码注释生成、代码解释、研…...
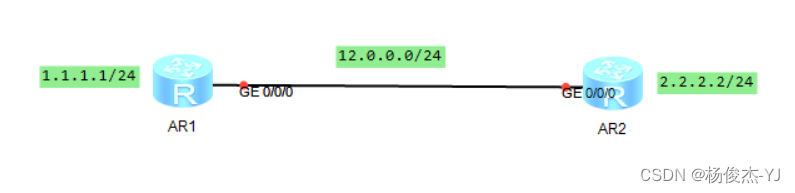
RIP协议(路由信息协议)
一、RIP协议概述 RIP协议(Routing Information Protocol,路由信息协议)是一种基于距离矢量的内部网关协议,即根据跳数来度量路由开销,进行路由选择。 相比于其它路由协议(如OSPF、ISIS等)&#…...

SpringBoot根据配置类动态加载不同环境下的自定义配置
dev环境配置 Profile({"dev","test"}) PropertySource("classpath:dev.properties") public class DevConfigLoader { }Profile("prod") PropertySource("classpath:prod.properties") public class ProdConfigLoader { }P…...
什么?穷哥们没钱RLHF?跟我一起DPO吧,丐版一样用
本次DPO训练采用TRL的方式来进行训练 Huggingface TRL是一个基于peft的库,它可以让RL步骤变得更灵活、简单,你可以使用这个算法finetune一个模型去生成积极的评论、减少毒性等等。 本次进行DPO的模型是一个500M的GPT-2,目的是训练快&#x…...
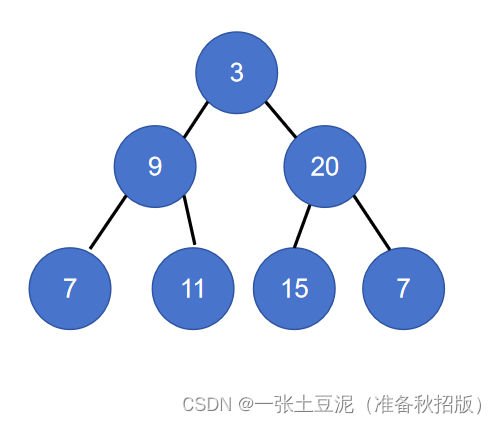
【Leetcode笔记】102.二叉树的层序遍历
目录 知识点Leetcode代码:ACM模式代码: 知识点 vector、queue容器的操作 对vector<int> vec;做插入元素操作:vec.push_back(x)。对queue<TreeNode*> que;做插入元素操作:que.push(root);。队列有四个常用的操作&…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
