java算法day43 | ● 1049. 最后一块石头的重量 II ● 494. 目标和 ● 474.一和零
1049. 最后一块石头的重量 II


核心思想: 尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。
是不是感觉和昨天讲解的416. 分割等和子集 (opens new window)非常像了。那么分成两堆石头,一堆石头的总重量是dp[target],另一堆就是sum - dp[target]。
class Solution {public int lastStoneWeightII(int[] stones) {int sum=0;for(int i=0;i<stones.length;i++){sum+=stones[i];}int target=sum/2;int dp[]=new int[target+1];//1、定义dp数组 3、第一列初始化为0for(int i=0;i<stones.length;i++){for(int j=target;j>=stones[i];j--){//4、遍历顺序dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);//2.递推公式}}return sum-dp[target]-dp[target];//最终的返回结果}
}
时间复杂度:O(m × n) , m是石头总重量(准确的说是总重量的一半),n为石头块数
空间复杂度:O(m)
494. 目标和


思路: 这道题的dp数组的含义变了。具体看代码随想录的讲解
class Solution {public int findTargetSumWays(int[] nums, int target) {int sum=0;for(int i=0;i<nums.length;i++){sum+=nums[i];}//如果不能满足(target+sum)/2为整数的条件或target的绝对值大于sum的绝对值,直接返回0if((target+sum)%2!=0 || Math.abs(target)>Math.abs(sum)) return 0;int size=(target+sum)/2;int[] dp=new int[size+1];//1、定义dp数组,表示j容量时的表达式数目dp[0]=1;//3、初始化for(int i=0;i<nums.length;i++){for(int j=size;j>=nums[i];j--){//4、因为是01背包,所以反向遍历dp[j]=dp[j]+dp[j-nums[i]];//2、递推公式}}return dp[size];}
}
时间复杂度:O(n × m),n为正数个数,m为背包容量
空间复杂度:O(m),m为背包容量
474.一和零

思路: 这道题是一个二维的背包问题,和普通的背包相比只需要多一层对容量的循环。

class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][] dp=new int[m+1][n+1];//1、定义dp数组,表示当0的容量为x,1的容量为n时,最大子集的长度for(int i=0;i<strs.length;i++){//4、遍历顺序,物品正序遍历int weightm=0;int weightn=0;for(int j=0;j<strs[i].length();j++){if(strs[i].charAt(j)=='0') weightm++; else weightn++;}for(int x=m;x>=weightm;x--){//4、物品的空间占用逆序遍历for(int y=n;y>=weightn;y--){dp[x][y]=Math.max(dp[x][y],dp[x-weightm][y-weightn]+1);//2、递推公式,注意value是1}}}return dp[m][n];}
}
时间复杂度: O(kmn),k 为strs的长度
空间复杂度: O(mn)
相关文章:

java算法day43 | ● 1049. 最后一块石头的重量 II ● 494. 目标和 ● 474.一和零
1049. 最后一块石头的重量 II 核心思想: 尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。 是不是感觉和昨天讲解的416. 分割等和子集 (opens new window)非常像了。那么分成两堆石头,一堆石头的…...

练气第六天
问:ANR怎么分析? ANR问题,这其实是一个非常综合性的问题,因为anr会涉及CPU负载,内存空间大小,线程锁,GC回收,这里面每个点,都是非常考验我们基本功的。 分析ANR问题,需…...

认识 Redis 与 分布式
Redis 官网页面 Redis官网链接 Redis 的简介 Redis 是一个在内存中存储数据的中间件 一方面用于作为数据库,另一方面用于作为数据缓存,适用于分布式系统中 Redis 基于网络,进行进程间通信,把自己内存中的变量给别的进程…...
AWK进阶)
Linux初学(十二)AWK进阶
一、AWK 1.1 简介 AWK是Linux中重要的文本处理工具Linux三剑客只一处理的对象可以是一个具体的文件,也可以是一个命令的执行结果AWK按行读取文件,将每一行视为一条记录 案例一:获取系统中每个用户的uid 方法一:cat /etc/passwd |…...

文字识别 Optical Character Recognition,OCR CTC STN
文字识别 Optical Character Recognition,OCR 自然场景文本检测识别技术综述 将图片上的文字内容,智能识别成为可编辑的文本。 场景文字识别(Scene Text Recognition,STR) OCR(Optical Character Recognition, 光学字符识别)传统上指对输入扫描文档图像进行分析处理,识…...
四、MySQL读写分离之MyCAT
一、读写分离概述 1、什么是读写分离: 读写分离:就是将读写操作分发到不同的服务器,读操作分发到对应的服务器 (slave),写操作分发到对应的服务器(master) ① M-S (主从) 架构下&…...
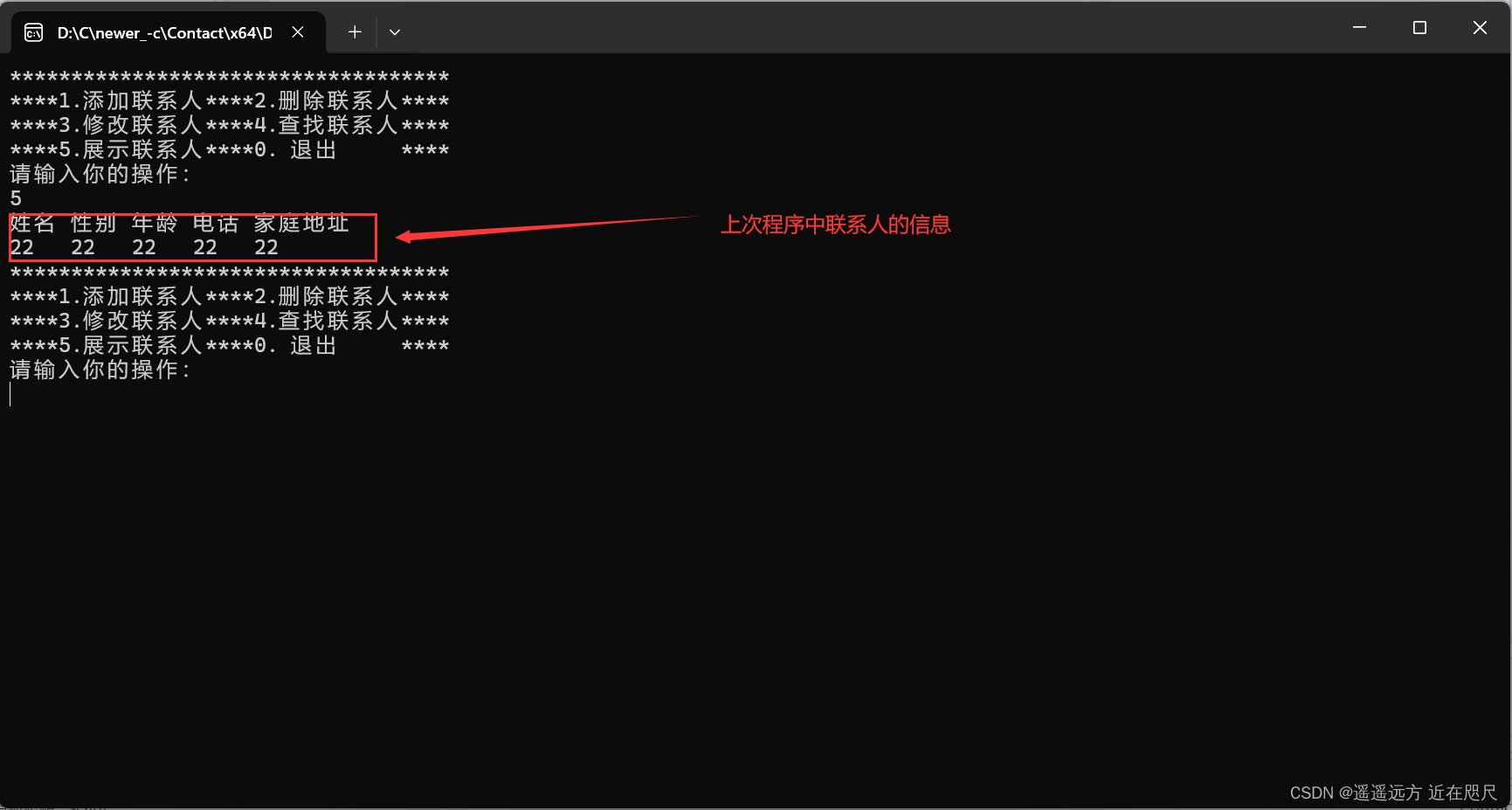
通讯录项目实现
引言:通过顺序表的逻辑实现通讯录。这里就不讲关于顺序表的函数了。如果有不明白的可以看我写的顺序表的博客。 目录 顺序表与通讯录的比较 各源文件文件大榄 Contact.c中通讯录相关函数的定义 初始化和销毁通讯录 添加联系人: 删除联系人…...

xss相关知识点与绕过思路总结
前言 对xss的绕过进行了系统的学习与实践后,重新审视一下xss,对他的绕过进行一个总结。 (当然我也是个小白,这些也是我当时瞎鸡儿乱搞绕过了几个xss自己做的小总结) 可能有点丑陋,献丑了。 好博客推荐 …...

深入解析语言模型:原理、实战与评估
引言 随着人工智能的飞速发展,语言模型作为自然语言处理(NLP)的核心技术之一,日益受到业界的广泛关注。本文旨在深入探讨语言模型的原理、实战应用以及评估方法,帮助读者更好地理解和应用这一技术。 一、语言模型原理…...

Elasticsearch 的索引优化常规项
优化常规项 https://blog.csdn.net/bairo007/article/details/132019575 1、按实际情况适当调整主分片的数量 如果主分片数量太少,会导致每个分片中的数据量过大,而且无法利用集群中所有节点的计算资源。如果主分片数量太多,会导致索引过度…...
)
【JavaParser笔记01】JavaParser解析Java源代码中的类信息(javadoc注释、类名称)
这篇文章,主要介绍如何使用JavaParser解析Java源代码中的类信息(javadoc注释、类名称)。 目录 一、JavaParser依赖库 1.1、引入依赖 1.2、获取类注释信息...
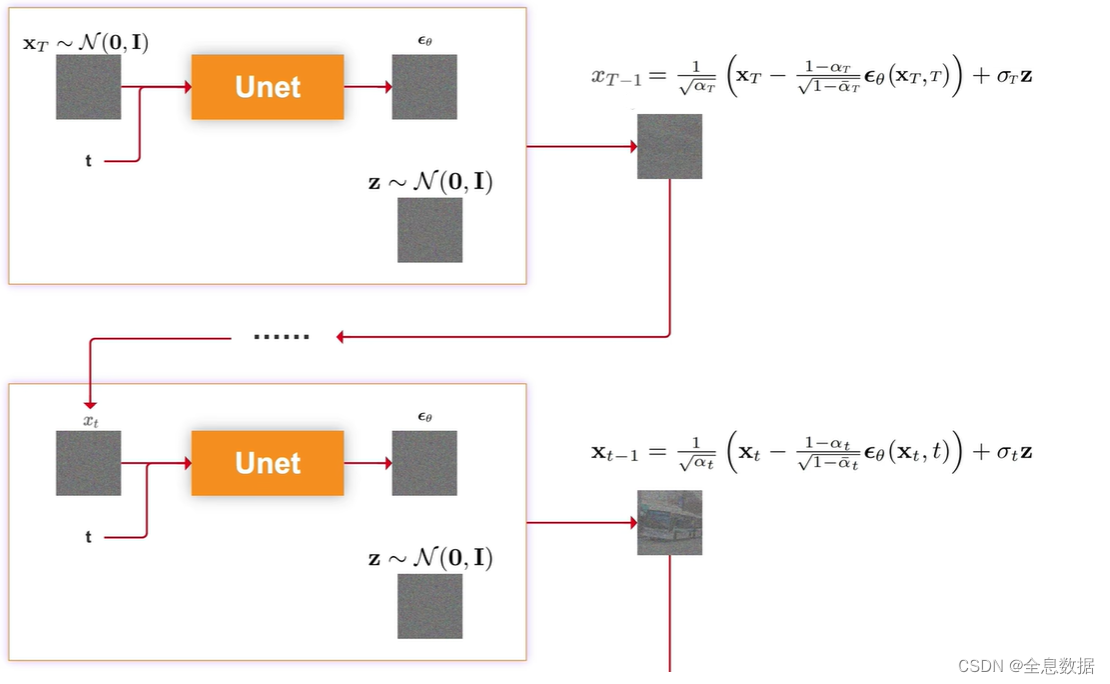
Stable Diffusion扩散模型【详解】小白也能看懂!!
文章目录 1、Diffusion的整体过程2、加噪过程2.1 加噪的具体细节2.2 加噪过程的公式推导 3、去噪过程3.1 图像概率分布 4、损失函数5、 伪代码过程 此文涉及公式推导,需要参考这篇文章: Stable Diffusion扩散模型推导公式的基础知识 1、Diffusion的整体…...

关于rabbitmq的prefetch机制
消息预取机制(Prefetch Mechanism)是RabbitMQ中用于控制消息传递给消费者的一种机制。它定义了在一个信道上,消费者允许的最大未确认的消息数量。一旦未确认的消息数量达到了设置的预取值,RabbitMQ就会停止向该消费者发送更多消息…...

机器学习介绍
机器学习是人工智能(AI)的一个分支,它使计算机系统能够从数据中学习并改进它们的性能。机器学习的核心在于开发算法,这些算法可以从大量数据中识别模式和特征,并用这些信息来做出预测或决策,而无需进行明确…...
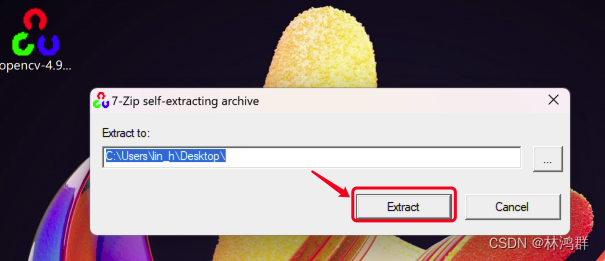
OpenCV4.9开发之Window开发环境搭建
1.打开OpenCV所在github地址 2.点击opencv仓库,进入仓库详情,点击右下方的OpenCV 4.9.0进入下载页面 3.点击opencv-4.9.0-windows.exe下载 开始下载中... 下载完成 下载完成后,双击运行解压,默认解压路径,修改为c:/...

DDD 中的实体和值对象有什么区别?
在DDD中,实体 Entity 和值对象 Value Object 是两个基本的概念,它们之间有一些重要的区别。 唯一性:实体是唯一的,每个实体都有一个唯一的标识符,即使它的属性在一段时间内发生了变化,它仍然是这个实体。与…...

算法-最值问题
#include<iostream> using namespace std; int main() {int a[7];//上午上课时间int b[7];//下午上课时间int c[7];//一天总上课时间for (int i 0; i < 7; i) {cin >> a[i] >> b[i];c[i] a[i] b[i];}int max c[0];//max记录最长时间int index -1;//索…...

Go 性能压测工具之wrk介绍与使用
在项目正式上线之前,我们通常需要通过压测来评估当前系统能够支撑的请求量、排查可能存在的隐藏bug;压力测试(压测)是确保系统在高负载情况下仍能稳定运行的重要步骤。通过模拟高并发场景,可以评估系统的性能瓶颈、可靠…...
)
数学思想论(有目录)
数学思想是数学发展过程中的重要指导原则,它涉及对数学概念、方法和理论的理解和认识,以及如何利用这些工具来解决实际问题。数学思想的形成和演进是随着数学的发展而逐渐深化的,它体现了人类对数学本质和应用的不断探索和思考。 一些主要的数学思想包括: 函数与方程思想…...
C++的并发世界(五)——线程状态切换
0.线程状态 初始化:该线程正在被创建; 就绪:该线程在列表中就绪,等待CPU调度; 运行:该线程正在运行; 阻塞:该线程被阻塞挂机,Blocked状态包括:pendÿ…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...
动态规划-1035.不相交的线-力扣(LeetCode)
一、题目解析 光看题目要求和例图,感觉这题好麻烦,直线不能相交啊,每个数字只属于一条连线啊等等,但我们结合题目所给的信息和例图的内容,这不就是最长公共子序列吗?,我们把最长公共子序列连线起…...
