蓝桥杯刷题day13——玩游戏【算法赛】
一、问题描述
小 A 和小 B 两个人在海边找到了 n 个石子,准备开始进行一些游戏,具体规则如下:小 B 首先将 n 个石子分成若干堆,接下来从小 A 开始小 A 和小 B 轮流取石子,每次可以任选一堆石子取走任意个,不可不取,没石子可取的输。问在最优策略的情况下,小 A 和小 B 到底谁能赢得游戏。
输入格式
一行一个整数 n,表示石子个数。
输出格式
一行一个字符 A 或者 B,输出 A 表示小 A 能赢得游戏,输出 B 表示小 B 能赢得游戏。
样例输入
2
样例输出
B
说明
对于 22 个石子,小 B 将其分成两堆,每堆 11 个石子即可获胜。
二、解析
首先,这个问题是一个经典的博弈问题,属于Nim游戏的一个变种。在这个游戏中,小A和小B轮流从若干堆石子中取走任意个石子,每次至少取一个,不能取石子的人输。
在这个特定的游戏规则下,石子堆的总数(即n)决定了游戏的胜负。对于小A来说,如果石子堆的总数是偶数,他无法确保自己总是能做出最优的选择,因为小B可以模仿小A的动作,保证每次轮到小A取石子时,石子堆的总数仍然是偶数。这样,最终当小B取完最后一堆石子后,小A将无石子可取,从而输掉游戏。
相反,如果石子堆的总数是奇数,小A可以采取一个策略,确保自己总能赢得游戏。他的策略是,每次小B取完石子后,他都取走一个石子,使得剩下的石子堆总数仍然是奇数。这样,无论小B如何取石子,小A总能保持石子堆的总数为奇数,直到最后小A取走最后一个石子,赢得游戏。
因此,这个游戏的胜负完全取决于石子堆的总数n是否为偶数。如果n是偶数,小B将赢得游戏;如果n是奇数,小A将赢得游戏。
三、python代码
import os
import sys# 请在此输入您的代码
if int(input())%2==0:print("B")
else:print("A")四、运行结果

相关文章:

蓝桥杯刷题day13——玩游戏【算法赛】
一、问题描述 小 A 和小 B 两个人在海边找到了 n 个石子,准备开始进行一些游戏,具体规则如下:小 B 首先将 n 个石子分成若干堆,接下来从小 A 开始小 A 和小 B 轮流取石子,每次可以任选一堆石子取走任意个,…...

Three.js——scene场景、几何体位置旋转缩放、正射投影相机、透视投影相机
个人简介 👀个人主页: 前端杂货铺 🙋♂️学习方向: 主攻前端方向,正逐渐往全干发展 📃个人状态: 研发工程师,现效力于中国工业软件事业 🚀人生格言: 积跬步…...

springboot集成rabbitmq
一 添加pom <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-amqp</artifactId> </dependency>二,配置yml spring:rabbitmq:host: 192.168.56.200port: 5672username: adminpasswor…...

腾讯云轻量4核8G12M应用服务器性能测评和优惠价格表
腾讯云4核8G服务器价格:轻量4核8G12M优惠价格646元15个月、CVM S5服务器4核8G配置1437元买1年送3个月。腾讯云4核8G服务器支持多少人同时在线?支持30个并发数,可容纳日均1万IP人数访问。腾讯云百科txybk.com整理4核8G服务器支持多少人同时在线…...

判断点在多边形内的算法
在计算几何中,判定点是否在多边形内,是个非常有趣的问题。通常有两种方法: 一、Crossing Number(交叉数) 它计算从点P开始的射线穿过多边形边界的次数。当“交叉数”是偶数时,点在外面;当它是奇数时&…...

Network AIS Receiver R400N
目录 Introduction OVERVIEW BASIC FEATURES APPLICATIONS SPECIFICATIONS Introduction OVERVIEW The R400N provides a method of monitoring the position, speed and heading of AIS vessels within VHF range. It can decode of Class A, Class B, Aids to Navigat…...

JavaScript循环
JavaScript的循环有两种,一种是for循环,通过初始条件、结束条件和递增条件来循环执行语句块: var x 0; var i; for (i1; i<10000; i) { x x i; } x; // 50005000 for循环的3个条件都是可以省略的,如果没有退出循环的判断条件…...

9Proxy,跨境电商一站式解决方案
文章目录 跨境电商什么是跨境电商跨境电商的机遇跨境电商技术支撑 海外代理IP什么是海外代理IP海外代理IP的作用如何选择海外代理IP 9Proxy9Proxy的优势9Proxy的解决方案价格汇总搜索引擎优化市场调查多重核算数据抓取广告技术 价格上手体验注册登录下载安装数据采集 总结福利 …...
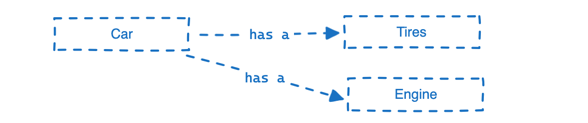
ObjectiveC-08-OOP面向对象程序设计-类的分离与组合
本节用一简短的文章来说下是ObjectiveC中的类。类其实是OOP中的一个概念,概念上简单来讲类是它是一组关系密切属性的集合,所谓的关系就是对现实事物的抽象。 上面提到的关系包括很多种,比如has a, is a,has some等&…...

Qt 总结
由于工作需要用到Qt。把过程中学习到的东西记录下来,希望能帮到他人和将来的自己。 由于需要快速实现需求,所以对Qt只是使用,并没有对原理的深入理解。 故此文只适合入门,不适合深入学习Qt。 文章目录 安装&维护示例&教…...
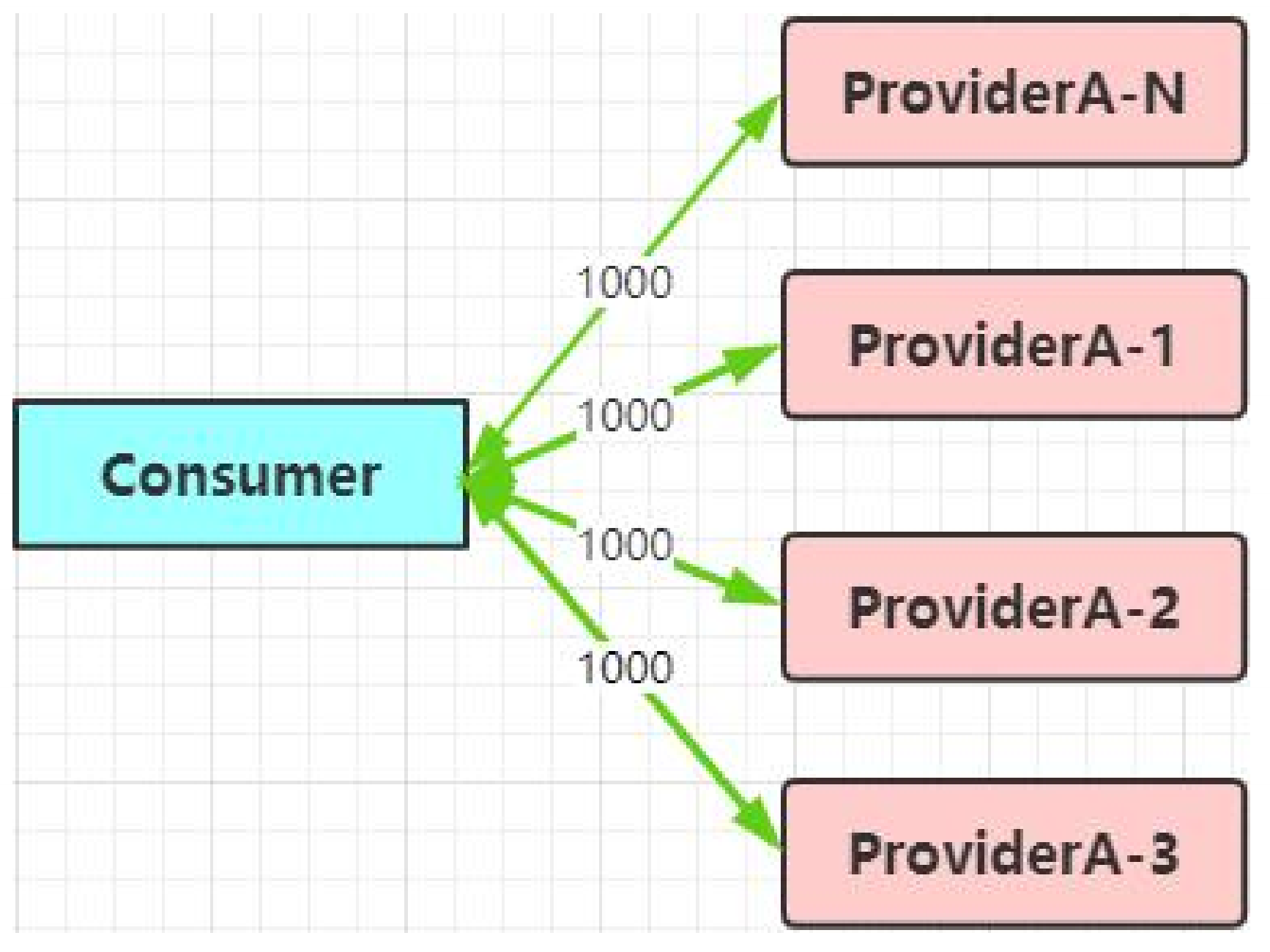
中间件复习之-RPC框架
什么是RPC框架? RPC(Remote Procedure Call):远程过程调用。当多个应用部署在多个服务器上时,由于他们不在一个内存空间上,因此需要网络来进行通信,而RPC允许它像调用本地方法一样调用远程服务。 RPC原理 服务消费方通过RPC客户…...

AcWing 787. 归并排序——算法基础课题解
AcWing 787. 归并排序 文章目录 题目描述CGo模板 题目描述 给定你一个长度为 n 的整数数列。 请你使用归并排序对这个数列按照从小到大进行排序。 并将排好序的数列按顺序输出。 输入格式 输入共两行,第一行包含整数 n。 第二行包含 n 个整数(所有…...
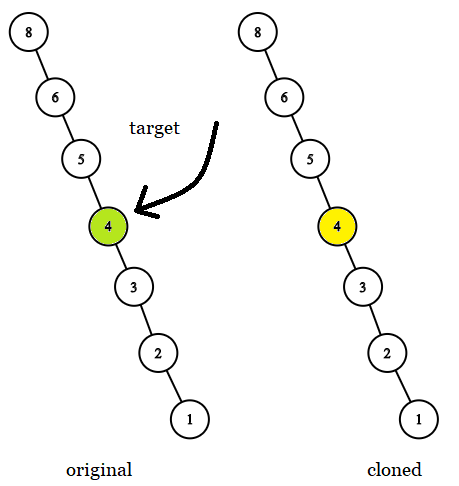
力扣1379---找出克隆二叉树的相同节点(Java、DFS、简单题)
目录 题目描述: 思路描述: 代码: (1): (2): 题目描述: 给你两棵二叉树,原始树 original 和克隆树 cloned,以及一个位于原始树 ori…...
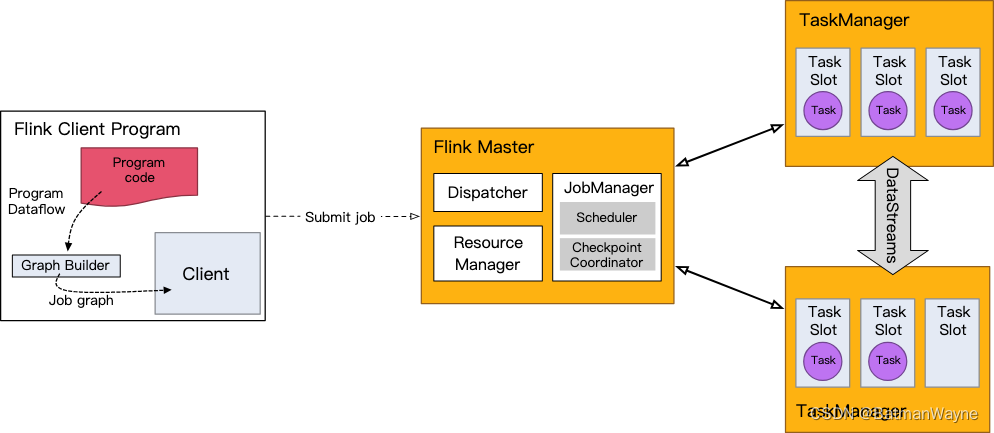
FLink学习(三)-DataStream
一、DataStream 1,支持序列化的类型有 基本类型,即 String、Long、Integer、Boolean、Array复合类型:Tuples、POJOs 和 Scala case classes Tuples Flink 自带有 Tuple0 到 Tuple25 类型 Tuple2<String, Integer> person Tuple2.…...
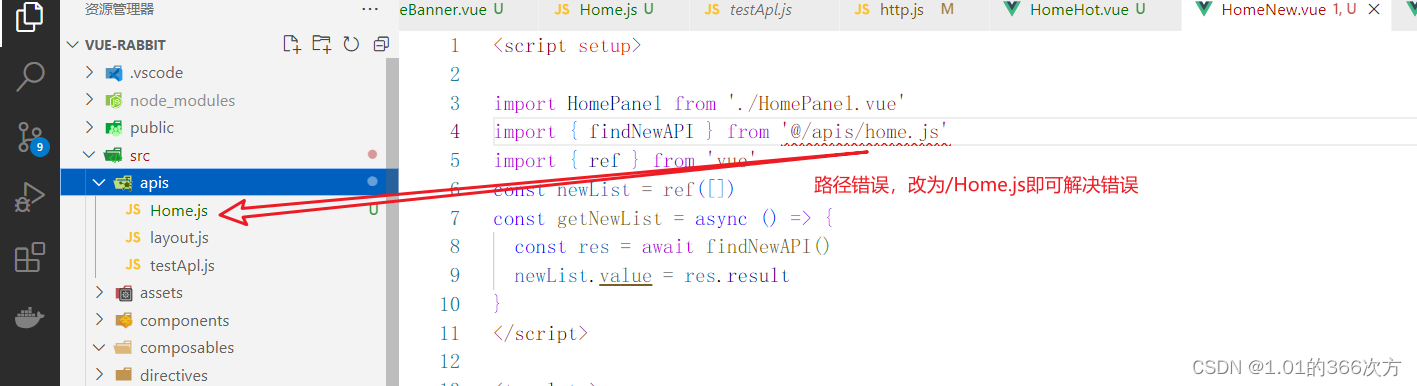
Failed to resolve import “Home/components/HomeNew.vue“. Does the file exist?
错误信息 [plugin:vite:import-analysis] Failed to resolve import "/apis/home.js" from "src/views/Home/components/HomeNew.vue". Does the file exist? 错误原因 路径错误 解决方法...

《价值》-张磊-高瓴资本-3-建立人脉和信任;顺应趋势,把握机遇;
第三章 价值投资初试炼 2005.6.1 创办高瓴资本 许多人问我为什么一直在创业,其实我倒没想到自己非要创业成功不可,只是觉得一定要做点事,做点有意义的事。归根到底,可能是“爱折腾,不满足现状,爱挑战自己”…...

游戏引擎中的物理应用
一、 角色控制器 Character Controller和普通的动态对象(Dynamic Actor )是不同的,主要的三个特点是: 它拥有可控制的刚体间的交互假设它是有无穷的摩擦力(可以站停在位置上),没有弹性加速和刹车几乎立即…...

复现k8s黄金票据学习
1.什么是黄金票据 在 Kubernetes 中,"黄金票据"并不是一个常见的术语。可能你想了解的是服务账户(Service Account)。服务账户是 Kubernetes 中用于身份验证和授权的一种机制。它们允许 Pods 或其他工作负载在 Kubernetes 集群中与…...

08-JavaScript BOM定时器及JS动画
1. 设置定时器 1.1设置超时定时器 超时调用需要使用window对象的setTimeout()方法,该方法接受两个参数:调用函数或计算表达式和以毫秒为单位的时间(即在执行代码前需要等待多少毫秒)。 //setTimeout(callback, after) //callba…...
边缘计算盒子与云计算:谁更适合您的业务需求?
边缘计算盒子和云计算,这两个概念听起来可能有点复杂,但其实它们就是两种不同的数据处理方式。那谁更适合您的业务需求呢?咱们来详细说说。 边缘计算盒子,就像是个小型的数据处理中心,放在离你业务现场比较近的地方。它…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
