垒骰子(爆搜/DP)
动态规划
- 方格取数
- 垒骰子
方格取数
题目描述
设有 N×NN \times NN×N 的方格图 (N≤9)(N \le 9)(N≤9),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 000。如下图所示(见样例):
A0 0 0 0 0 0 0 00 0 13 0 0 6 0 00 0 0 0 7 0 0 00 0 0 14 0 0 0 00 21 0 0 0 4 0 00 0 15 0 0 0 0 00 14 0 0 0 0 0 00 0 0 0 0 0 0 0B
某人从图的左上角的 AAA 点出发,可以向下行走,也可以向右走,直到到达右下角的 BBB 点。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字 000)。
此人从 AAA 点到 BBB 点共走两次,试找出 222 条这样的路径,使得取得的数之和为最大。
输入格式
输入的第一行为一个整数 NNN(表示 N×NN \times NN×N 的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的 000 表示输入结束。
输出格式
只需输出一个整数,表示 222 条路径上取得的最大的和。
样例 #1
样例输入 #1
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
样例输出 #1
67

注意这里需要分为 i和j 是否相等,如果不相等一定不在同一个格子中,那就可以取两次了,为什么可以优化成三维,是因为如果走的次数是固定的,横坐标和纵坐标的和事固定的(行数+列数)。
注意,有了步数这一实际意义(大于等于0)和 步数与行数之间的约束(后者必须小于前者),循环的嵌套顺序和行数循环终止条件要注意
#include <iostream>
using namespace std;
//#define int long long int
const int N=10;
int a[N][N];
int dp[N][N][N][N];
int n,x,y,s;
int get_max(int u,int v,int o,int p){return max(max(u,v),max(o,p));
}
signed main(int argc, char** argv) {cin>>n;while(cin>>x>>y>>s){if(!x&&!y&&!s)break;a[x][y]=s;}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){for(int k=1;k<=n;k++){for(int l=1;l<=n;l++){dp[i][j][k][l]=get_max(dp[i-1][j][k-1][l],dp[i-1][j][k][l-1],dp[i][j-1][k-1][l],dp[i][j-1][k][l-1])+a[i][j]+a[k][l];
// 两个人一步有四种结果if(i==k&&j==l)dp[i][j][k][l]-=a[i][j];}}}}cout<<dp[n][n][n][n];return 0;
}#include <iostream>
using namespace std;
//#define int long long int
const int N=10;
int a[N][N];
int dp[N][N][N*2];
int n,x,y,s;
int get_max(int u,int v,int o,int p){return max(max(u,v),max(o,p));
}
signed main(int argc, char** argv) {cin>>n;while(cin>>x>>y>>s){if(!x&&!y&&!s)break;a[x][y]=s;}dp[1][1][0]=a[1][1];//初始化for(int k=1;k<=(n-1)*2;k++){//已经走了多少步(两个人是同时走一步)for(int i=1;i<=min(k+1,n);i++){for(int j=1;j<=min(k+1,n);j++){dp[i][j][k]=get_max(dp[i-1][j][k-1],dp[i-1][j-1][k-1],dp[i][j][k-1],dp[i][j-1][k-1])+a[i][k+2-i]+a[j][k+2-j];
// 两个人一步有四种结果 p1向下p2向右,都向下,都向右,p1向右p2向下if(i==j)dp[i][j][k]-=a[i][k+2-i];
// m行n列总共 m-1+n-1步
// cx行,cx=i,cy列 cx-1+cy-1=k步 cy=k+2-cx }}}cout<<dp[n][n][(n-1)*2];return 0;}
//1 1 1
//2 2 3
//2 3 4垒骰子

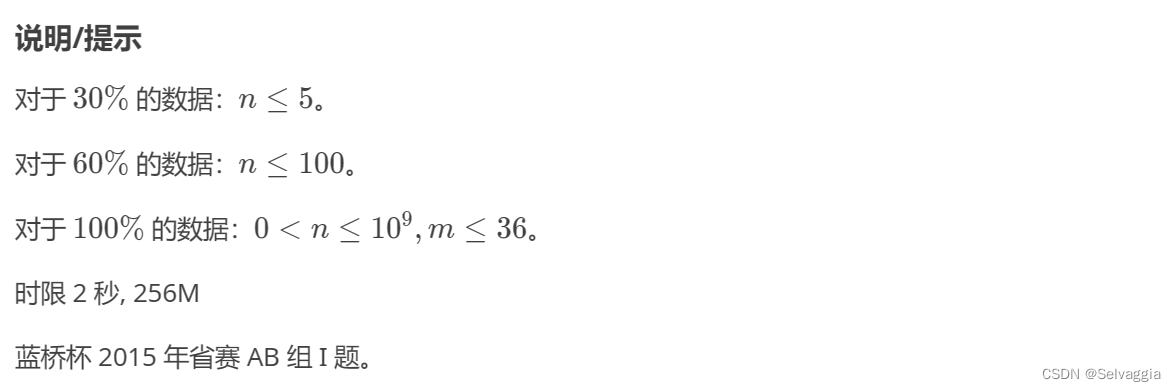
爆搜
#include <iostream>
using namespace std;
#define int long long int
const int mod=1e9+7;
const int N=10;
int m,n,x,y;
int back[7];
bool conflict[40][40];
int dfs(int u,int cnt){if(cnt==n+1){return 1;}int ans=0;for(int down=1;down<=6;down++){//枚举骰子底部的数字if(conflict[u][down])continue;ans=(ans+dfs(back[down],cnt+1))%mod;}
}
int quickpow(int b,int e){b%=mod;int res=1;while(e){if(e&1)res=res*b%mod;b=b*b%mod;e=e>>1;}return res;
}
signed main(int argc, char** argv) {back[1]=4;back[4]=1;back[2]=5;back[5]=2;back[3]=6;back[6]=3;cin>>n>>m;for(int i=0;i<m;i++){cin>>x>>y;conflict[x][y]=true;conflict[y][x]=true;}int res=0;for(int down=1;down<=6;down++){res=(res+dfs(back[down],2))%mod;}res=res*quickpow(4,n)%mod;cout<<res;return 0;}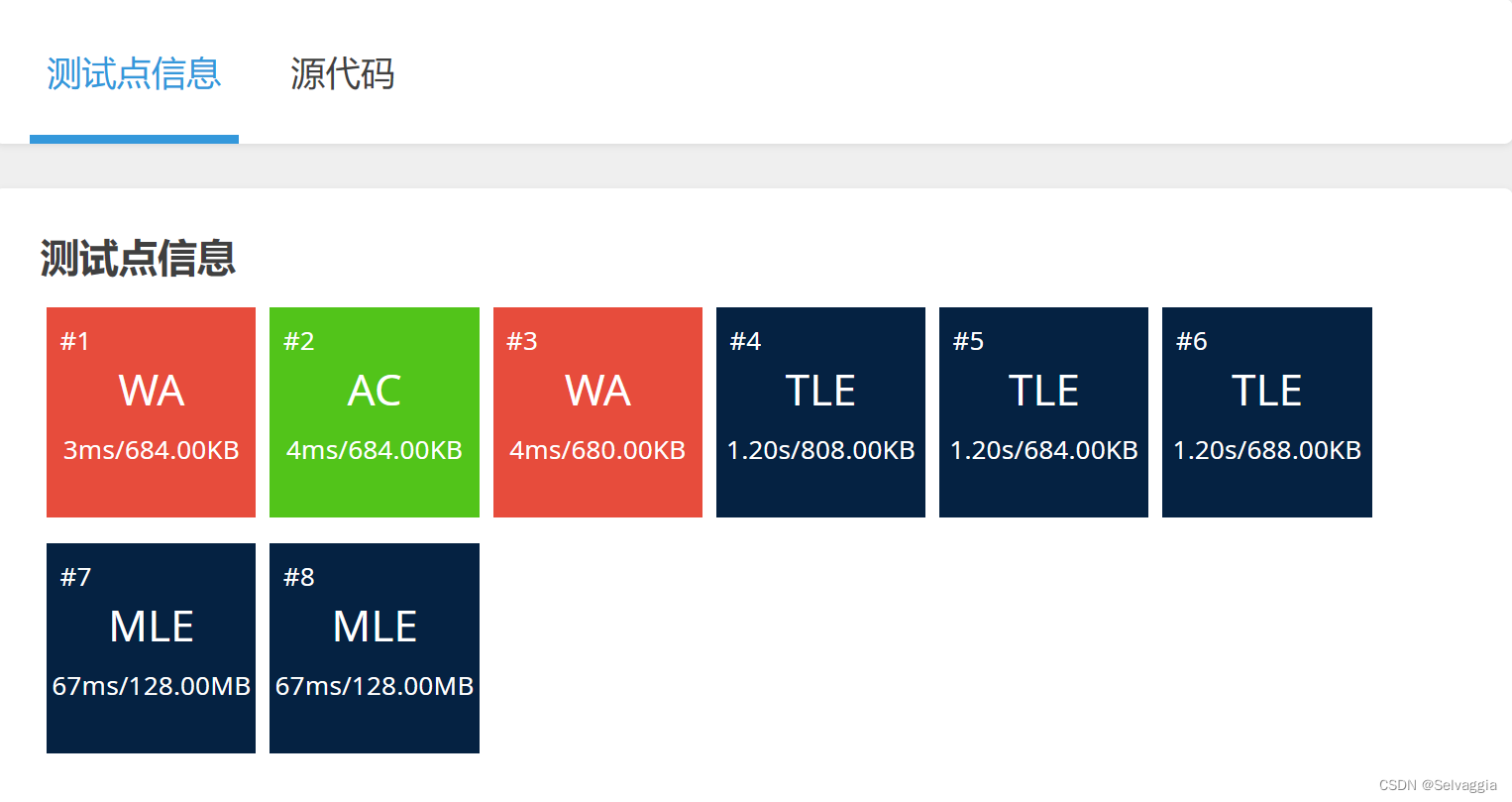
在这种解题方式上用快速幂有些多余。分枝过多的递归当n=100时,几乎不能在题目规定时间内计算出来。当n<100时,通过累乘的方式将4一次、一次乘给ans,这并不会对程序的效率造成很大影响。
相关文章:

垒骰子(爆搜/DP)
动态规划方格取数垒骰子方格取数 题目描述 设有 NNN \times NNN 的方格图 (N≤9)(N \le 9)(N≤9),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 000。如下图所示(见样例): A0 0 0 0 0 0 0 00 0 13 0 …...

Telink之标准SDK的介绍_1
前提:常见的项目架构:应用层----》驱动层----》硬件层 1、软件组织架构 顶层⽂件夹( 8 个): algorithm,application,boot,common,drivers,proj_lib,stack,v…...

JNI内两种方式从C/C++中传递一维、二维、三维数组数据至Java层详细梳理
目录 0 前言 1 准备工作介绍 2 一维数组 2.1 return形式 2.2 参数形式 3 二维数组 3.1 return形式 3.2 参数形式 4 三维数组 4.1 return形式 4.2 参数形式 5 测试代码 6 结果说明 0 前言 就如之前我写过的一篇文章【JNI内形参从C代码中获取返回值并返回到Java层使…...
)
快递计费系统--课后程序(Python程序开发案例教程-黑马程序员编著-第3章-课后作业)
实例5:快递计费系统 快递行业高速发展,我们邮寄物品变得方便快捷。某快递点提供华东地区、华南地区、华北地区的寄件服务,其中华东地区编号为01、华南地区编号为02、华北地区编号为03,该快递点寄件价目表具体如表1所示。 表1 寄…...

JS - 自定义一周的开始和结束,计算日期所在月的周数、所在月第几周、所在周的日期范围
自定义一周的开始和结束,计算日期所在月的周数、所在月第几周、所在周的日期范围一. 方法使用二. 实现案例一. 方法使用 根据月开始日期星期几、月结束日期星期几,计算始周、末周占月的天数(每周周期段:上周六 —— 本周五&#x…...

Linux :理解编译的四个阶段
目录一、了解编译二、认识编译的四个阶段(一)预处理(二)编译(三)汇编(四)链接1.静态链接2.动态链接三、分步编译(一)创建.c文件(二)预…...

197.Spark(四):Spark 案例实操,MVC方式代码编程
一、Spark 案例实操 1.数据准备 电商网站的用户行为数据,主要包含用户的 4 种行为:搜索,点击,下单,支付 样例类: 2. Top10 热门品类 先按照点击数排名,靠前的就排名高;如果点击数相同,再比较下单数;下单数再相同,就比较支付数。 我们有多种写法,越往后性能越…...
Vue 项目如何迁移小程序
最近我们看到有开发者在社群里提出新的疑惑「我手头已经有一个成熟的 HTML5 项目了,这种项目可以转为小程序在 FinClip 环境中运行吗?」。 经过工作人员的沟通了解,开发者其实是想将已有的 Vue 项目转为小程序,在集成了 FinClip …...

unit1-问候以及介绍
unit1-问候以及介绍 重点表达 1、问好 使用hello 和 hi 来打招呼。hello可以使用在正式和非正式的场合。hi是非正式的。但是hello 和 hi 都可以在一天的任何时段使用。 Hello. 你好。 Hi! 嗨! 介绍你的姓名 使用 I’m 和 My name is 告诉别人你的名字。 I’m Pau…...
杂记——19.git上传时出现the remote end hung up unexpectedly错误
git是大家常用的项目版本控制工具,熟练地使用git可以提高开发效率,但是有时在使用git推送代码时,会提示“the remote end hung up unexpectedly”的问题,那么git推送代码提示“the remote end hung up unexpectedly”怎么解决呢&a…...

python123平台题目
作业二 1. 2的n次方描述输入格式输出格式输入输出实例代码解析2. 输出最大值描述输入格式输出格式输入输出示例代码解析3. 字符串输出描述输入格式输出格式输入输出示例代码解析4. 字符串长度描述输入格式输出格式输入输出示例代码解析...
:TF坐标变换)
ROS学习笔记(六):TF坐标变换
ROS学习笔记(六):TF坐标变换TF的基本知识TF工具tf_monitortf_echostatic_transform_publisherview_frames创建TF广播器创建TF监听器TF的基本知识 TF是一个让用户随时间跟踪多个坐标系的功能包,它使用树形数据结构,根据…...

【python】为你绘制玫瑰一束,爱意永存
前言 嗨喽~大家好呀,这里是魔王呐 ❤ ~! 若是有真情,爱意如溪水, 若是有真爱,爱意如阳光, 若是两情相悦,又岂在朝朝暮暮, 女子淡淡的情愫,深深地想念, 浓浓的爱意&a…...
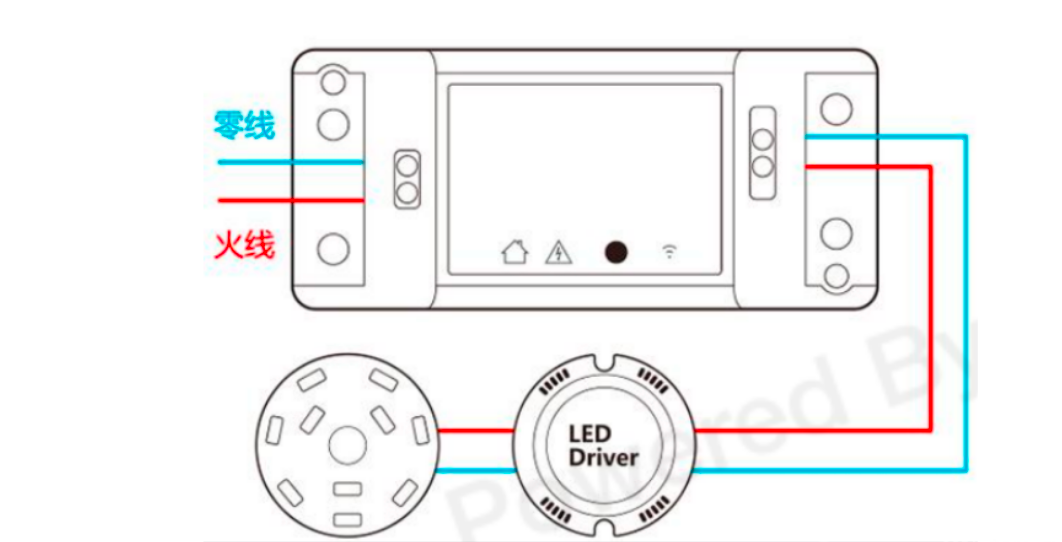
智能家居创意产品一Homkit智能通断器
智能通断器,也叫开关模块,可以非常方便地接入家中原有开关、插座、灯具、电器的线路中,通过手机App或者语音即可控制电路通断,轻松实现原有家居设备的智能化改造。 随着智能家居概念的普及,越来越多的人想将自己的家改…...
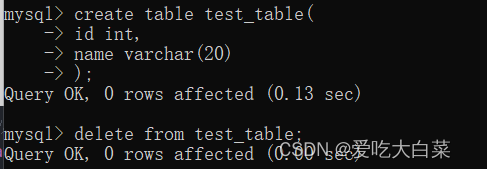
【数据库】MySQL表的增删改查(基础命令详解)
写在前面 : 语法中大写字母是关键字,用[]括这的是可以省略的内容。文中截图是相对应命令执行完得到的结果截图。1.CRUD 注释:在SQL中可以使用“--空格描述”来表示注释说明.CRUD:即增加(Create)、查询(Retrieve)、更新(Update)、删除(Delete)四个单词的首…...

2023年全国最新保安员精选真题及答案15
百分百题库提供保安员考试试题、保安职业资格考试预测题、保安员考试真题、保安职业资格证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 151.该图所要表达的是()消防器材。 A:地上消防栓 B:灭火器 …...

KPN对任意形状文本检测
文章目录一、研究背景二、方法流程1. 特征提取2. 核建议3. 实例无关特征图4. 轮廓生成5. 其余部分内容三、不足一、研究背景 相比起基于 FCN 网络的文本边缘检测网络,KPN网络可以更好地处理文本之间的间隔。 二、方法流程 1. 特征提取 FCN 和 FPN FCN(全卷积神经…...

同城外卖跑腿系统源码分析
外卖订餐已经成为很多“社畜”日常不可分割的一部分,足不出户,只需要一部电子设备即可在线订餐,并且可提供的选择非常多样化,与传统的电话订餐外卖模式相比也更便捷的多。 因此,同城外卖跑腿系统源码得以爆火ÿ…...
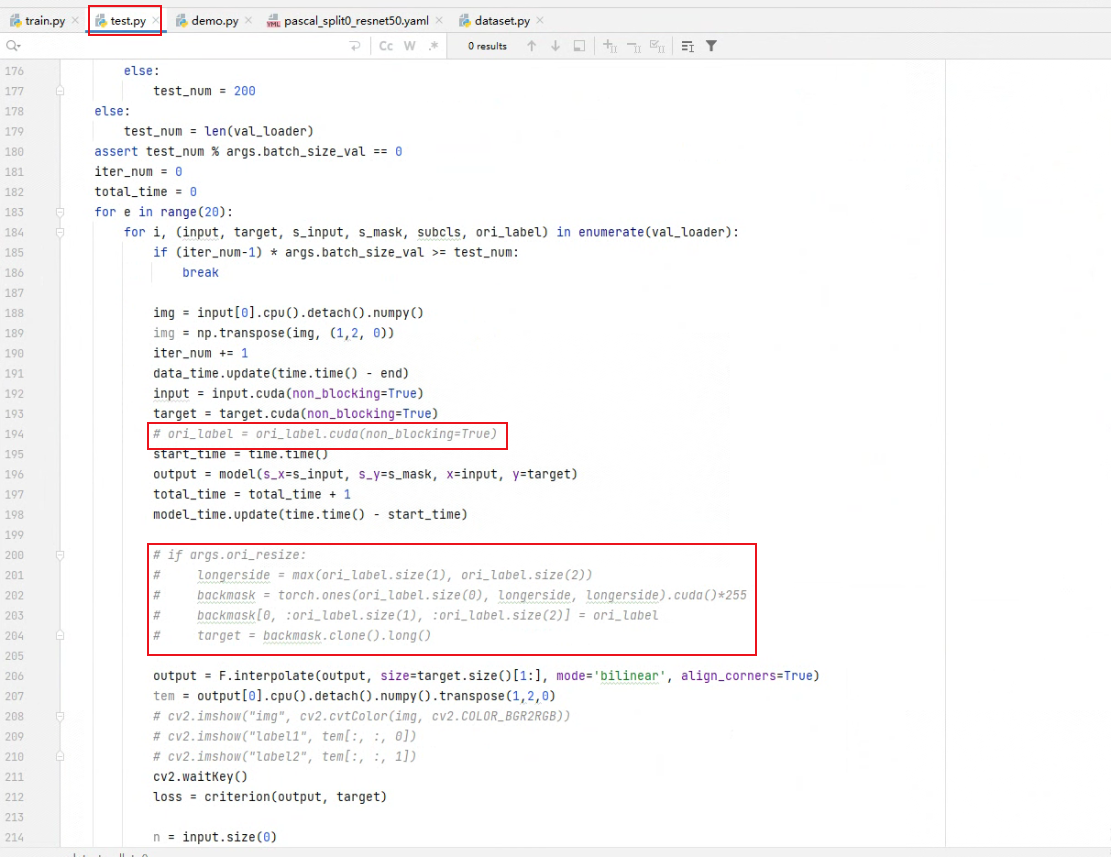
SCL_PFENET跑通填坑
1.数据准备:VOC2012数据集,initmodel文件夹(预训练模型),SegmentationClassAug数据2.训练部分:训练部分没什么需要改动的,也就改一下选择的配置文件。在config文件夹里有关于coco和voc数据的配置…...
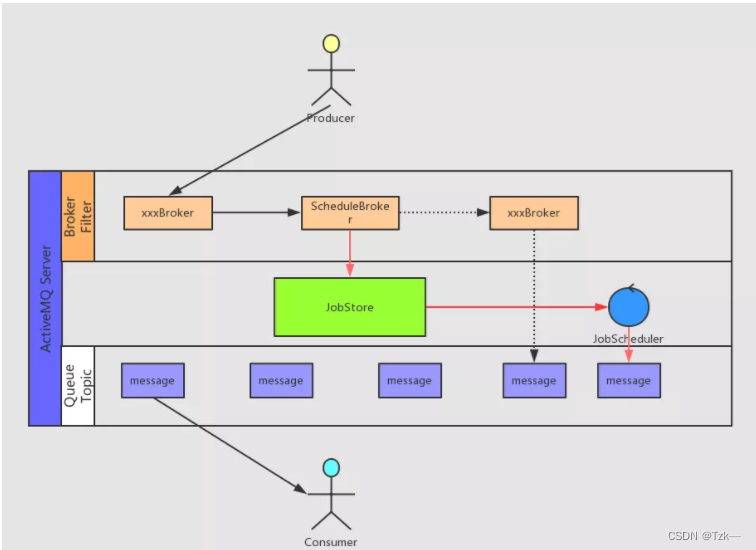
Redis 做延迟消息队列
背景 看到消息队列,我们肯定会想到各种MQ,比如:RabbitMQ,acivityMQ、RocketMQ、Kafka等。 但是,当我们需要使用消息中间件的时候,并非每次都需要非常专业的消息中间件,假如我们只有一个消息队…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...

VSCode 使用CMake 构建 Qt 5 窗口程序
首先,目录结构如下图: 运行效果: cmake -B build cmake --build build 运行: windeployqt.exe F:\testQt5\build\Debug\app.exe main.cpp #include "mainwindow.h"#include <QAppli...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...
