蓝桥杯第十四届C++A组(未完)
【规律题】平方差
题目描述
给定 L, R,问 L ≤ x ≤ R 中有多少个数 x 满足存在整数 y,z 使得 。
输入格式
输入一行包含两个整数 L, R,用一个空格分隔。
输出格式
输出一行包含一个整数满足题目给定条件的 x 的数量。
样例输入
1 5
样例输出
4
提示
对于 40% 的评测用例,LR ≤ 5000 ;
对于所有评测用例,1 ≤ L ≤ R ≤ 10^9 。
由得
,
令 ,则
,解得:
要使y和z有整数解,那么 为偶数,
(1)偶数+偶数=偶数,偶数-偶数=偶数;
(2)奇数+奇数=偶数,奇数-奇数=偶数;
则m和n奇偶性相同,即如果x有一对因子奇偶性相同,那么一定可以找到y,z满足。
(1)若m,n都为偶数,那么m是2的倍数,n是2的倍数,那么m*n一定是4的倍数。
(2)若m,n都为奇数,那么由性质 奇数*奇数=奇数 得,m*n也一定为奇数。
综上 x 是四的倍数或者奇数。
#include<iostream>
#include<cstring>
#include<map>
#include<vector>
#include<cmath>
using namespace std;
typedef long long LL;
const int N=10010;
int main(){LL L,R;cin>>L>>R;int cnt=0;for(LL i=L;i<=R;i++){if(i%4==0||i%2){cnt++;}}cout<<cnt<<endl;return 0;
}更小的数
题目描述
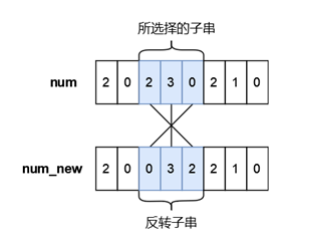
小蓝有一个长度均为 n 且仅由数字字符 0 ∼ 9 组成的字符串,下标从 0 到 n − 1,你可以将其视作是一个具有 n 位的十进制数字 num,小蓝可以从 num 中选出一段连续的子串并将子串进行反转,最多反转一次。小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字 numnew 满足条件 numnew < num,请你帮他计算下一共有多少种不同的子串选择方案,只要两个子串在 num 中的位置不完全相同我们就视作是不同的方案。
注意,我们允许前导零的存在,即数字的最高位可以是 0 ,这是合法的。
输入格式
输入一行包含一个长度为 n 的字符串表示 num(仅包含数字字符 0 ∼ 9),
从左至右下标依次为 0 ∼ n − 1。
输出格式
输出一行包含一个整数表示答案。
样例输入
210102
样例输出
8
提示
一共有 8 种不同的方案:
1)所选择的子串下标为 0 ∼ 1 ,反转后的 numnew = 120102 < 210102 ;
2)所选择的子串下标为 0 ∼ 2 ,反转后的 numnew = 012102 < 210102 ;
3)所选择的子串下标为 0 ∼ 3 ,反转后的 numnew = 101202 < 210102 ;
4)所选择的子串下标为 0 ∼ 4 ,反转后的 numnew = 010122 < 210102 ;
5)所选择的子串下标为 0 ∼ 5 ,反转后的 numnew = 201012 < 210102 ;
6)所选择的子串下标为 1 ∼ 2 ,反转后的 numnew = 201102 < 210102 ;
7)所选择的子串下标为 1 ∼ 4 ,反转后的 numnew = 201012 < 210102 ;
8)所选择的子串下标为 3 ∼ 4 ,反转后的 numnew = 210012 < 210102 ;
对于 20% 的评测用例,1 ≤ n ≤ 100 ;
对于 40% 的评测用例,1 ≤ n ≤ 1000 ;
对于所有评测用例,1 ≤ n ≤ 5000 。
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<vector>
#include<cmath>
using namespace std;
typedef long long LL;
int main(){string s;cin>>s;int n=s.size();int cnt=0;for(int i=0;i<n-1;i++){for(int j=n-1;j>i;j--){if(s[i]>s[j]) cnt++;else if(s[i]==s[j]){for(int x=i,y=j;x<y;x++,y--){if(s[x]>s[y]){cnt++;break;}else if(s[x]<s[y]) break;}}}}cout<<cnt<<endl;return 0;
}【DFS】颜色平衡树
题目描述
给定一棵树,结点由 1 至 n 编号,其中结点 1 是树根。树的每个点有一个颜色 Ci。
如果一棵树中存在的每种颜色的结点个数都相同,则我们称它是一棵颜色平衡树。
求出这棵树中有多少个子树是颜色平衡树。
输入格式
输入的第一行包含一个整数 n ,表示树的结点数。
接下来 n 行,每行包含两个整数 Ci , Fi,用一个空格分隔,表示第 i 个结点的颜色和父亲结点编号。
特别地,输入数据保证 F1 为 0 ,也即 1 号点没有父亲结点。保证输入数据是一棵树。
输出格式
输出一行包含一个整数表示答案。
样例输入
6 2 0 2 1 1 2 3 3 3 4 1 4
样例输出
4
提示
编号为 1, 3, 5, 6 的 4 个结点对应的子树为颜色平衡树。
对于 30% 的评测用例,n ≤ 200,Ci ≤ 200 ;
对于 60% 的评测用例,n ≤ 5000,Ci ≤ 5000 ;
对于所有评测用例,1 ≤ n ≤ 200000,1 ≤ Ci ≤ 200000,0 ≤ Fi < i 。
#include<iostream>
#include<cstring>
#include<vector>
#include<map>
using namespace std;
const int N=2e5+10;
int c[N];
int ans=0;
int n;
vector<int> g[N];
void add(map<int,int> &cnt,map<int,int> &cnt_nb){for(auto mp:cnt_nb){int x=mp.first;int y=mp.second;cnt[x]+=y;}
}
map<int,int> dfs(vector<int> *g,int *c,int i){int sz=g[i].size();map<int,int> cnt;if(sz==0){cnt[c[i]]=1;ans++;return cnt;}cnt[c[i]]=1;for(int j=0;j<sz;j++){int nb=g[i][j];map<int,int> cnt_nb=dfs(g,c,nb);add(cnt,cnt_nb);}int num=cnt[c[i]];for(auto mp:cnt){int count=mp.second;if(count!=num) return cnt;}ans++;return cnt;
}
int main(){cin>>n;for(int i=0;i<n;i++){int f;cin>>c[i]>>f;if(f>=1) g[f-1].push_back(i);}dfs(g,c,0);cout<<ans<<endl;return 0;
}【DFS】(选不选)买瓜
题目描述
小蓝正在一个瓜摊上买瓜。瓜摊上共有 n 个瓜,每个瓜的重量为 Ai 。
小蓝刀功了得,他可以把任何瓜劈成完全等重的两份,不过每个瓜只能劈一刀。
小蓝希望买到的瓜的重量的和恰好为 m 。
请问小蓝至少要劈多少个瓜才能买到重量恰好为 m 的瓜。如果无论怎样小蓝都无法得到总重恰好为 m 的瓜,请输出 −1 。
输入格式
输入的第一行包含两个整数 n, m,用一个空格分隔,分别表示瓜的个数和小蓝想买到的瓜的总重量。
第二行包含 n 个整数 Ai,相邻整数之间使用一个空格分隔,分别表示每个瓜的重量。
输出格式
输出一行包含一个整数表示答案。
样例输入
3 10 1 3 13
样例输出
2
提示
对于 20% 的评测用例,∑n≤10;
对于 60% 的评测用例,∑n≤20;
对于所有评测用例,1 ≤n≤30,1≤ Ai ≤ 10^9 ,1 ≤ m ≤ 10^9
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
const int N=35,INF=0x3f3f3f3f;
LL p[N];
LL a[N];
int n;
LL m;
int ans=INF;
void dfs(int u,LL sum,int cnt){if(sum==m){ans=min(ans,cnt);return ;}if(cnt>=ans||u>n||sum+p[u]<m||sum>m) return ;dfs(u+1,sum+a[u],cnt);dfs(u+1,sum+a[u]/2,cnt+1);dfs(u+1,sum,cnt);
}
int main(){cin>>n>>m;m*=2;for(int i=1;i<=n;i++){cin>>a[i];a[i]*=2;}sort(a+1,a+1+n,greater<int>());for(int i=n;i>=1;i--) p[i]=p[i+1]+a[i];dfs(1,0,0);if(ans==INF) cout<<"-1"<<endl;else cout<<ans<<endl;return 0;
}网络稳定性(X)
异或和之和
题目描述
给定一个数组 Ai,分别求其每个子段的异或和,并求出它们的和。或者说,对于每组满足 1 ≤ L ≤ R ≤ n 的 L, R ,求出数组中第 L 至第 R 个元素的异或和。然后输出每组 L, R 得到的结果加起来的值。
输入格式
输入的第一行包含一个整数 n 。
第二行包含 n 个整数 Ai ,相邻整数之间使用一个空格分隔。
输出格式
输出一行包含一个整数表示答案。
样例输入
5 1 2 3 4 5
样例输出
39
提示
对于 30% 的评测用例,n ≤ 300 ;
对于 60% 的评测用例,n ≤ 5000 ;
对于所有评测用例,1 ≤ n ≤ 105,0 ≤ Ai ≤ 2^20 。
区间[l,r]的异或和可以表示为,这样原问题就变成了:求n+1个数两两异或之和,如果
的二进制第 j 位为1(0),我们只需知道 [0,i-1] 这个区间内的数二进制第 j 位为0(1)的个数x,这样s[i]的第 j 位的贡献值为x*2^j;
#include<iostream>
#include<vector>
#include<map>
#define int long long
using namespace std;
const int N=1e5+10;
int a[N][30];
signed main(){int n;cin>>n;int x;for(int i=1;i<=n;i++){cin>>x;for(int j=0;j<=20;j++){a[i][j]=(x>>j)&1;a[i][j]^=a[i-1][j];}}int ans=0;for(int j=0;j<=20;j++){map<int,int> mp;mp[0]++;for(int i=1;i<=n;i++){int x=mp[a[i][j]^1];//与第i个数第j位不同的个数ans+=(1<<j)*x;mp[a[i][j]]++;}}cout<<ans<<endl;return 0;
}#include<iostream>
#include<vector>
#include<map>
#define int long long
using namespace std;
const int N=1e5+10;
int a[N];
int s[N];
int cnt[N][30];
signed main(){int n;cin>>n;int x;for(int i=1;i<=n;i++){cin>>a[i];s[i]=s[i-1]^a[i];}
//求n+1个数第j位0和1的个数for(int j=0;j<=20;j++){for(int i=0;i<=n;i++){if(s[i]>>j&1) cnt[j][1]++;else cnt[j][0]++;}}int ans=0;for(int i=0;i<=20;i++){
//每个1都可以和每个0异或等于1,总数为cnt[i][0]*cnt[i][1],每个1的贡献值为2^ians+=cnt[i][0]*cnt[i][1]*(1<<i);}cout<<ans<<endl;return 0;
}像素放置(X)
翻转硬币(X)
相关文章:
蓝桥杯第十四届C++A组(未完)
【规律题】平方差 题目描述 给定 L, R,问 L ≤ x ≤ R 中有多少个数 x 满足存在整数 y,z 使得 。 输入格式 输入一行包含两个整数 L, R,用一个空格分隔。 输出格式 输出一行包含一个整数满足题目给定条件的 x 的数量。 样例输入 1 5 样例输出 …...

职场口才提升之道
职场口才提升之道 在职场中,口才的重要性不言而喻。无论是与同事沟通协作,还是向上级汇报工作,亦或是与客户洽谈业务,都需要具备良好的口才能力。一个出色的职场人,除了拥有扎实的专业技能外,还应具备出色…...
【算法练习】28:选择排序学习笔记
一、选择排序的算法思想 弄懂选择排序算法,先得知道两个概念:未排序序列,已排序序列。 原理:以升序为例,选择排序算法的思想是,先将整个序列当做未排序的序列,以序列的第一个元素开始。然后从左…...
【关于窗口移动求和的两种计算方法】
窗口移动计算方法 例子方法1方法2运行结果: 例子 在很多算法中都会涉及到窗口滑动,比如基于新息序列更新的自适应卡尔曼滤波器算法中便会使用到。 已知一个数列:OCV [1;2;3;4;5;6;7;8;9;10;11;12;13;14;15],定义窗口长度为5,每次…...

Win10文件夹共享(有密码的安全共享)(SMB协议共享)
前言 局域网内(无安全问题,比如自己家里wifi)无密码访问,参考之前的操作视频 【电脑文件全平台共享、播放器推荐】手机、电视、平板播放硬盘中的音、视频资源 下面讲解公共网络如办公室网络、咖啡厅网络等等环境下带密码的安全…...

Client sent an HTTP request to an HTTPS server
背景 最近踩坑了 我发现域名:8000可以访问我的服务 但是域名:443却不行,这很反常 结果发现是nginx配置的问题,需要把http改成https! 原因 如果你的后端服务(运行在8000端口上)已经配置了SS…...

Springboot传参要求
Web.java(这里定义了一个实体类交Web) public class Web{ private int Page; public int getPage() {return Page;}public void setPage(int page) {Page page;} } 1、通过编译器自带的getter、Setter传参 。只是要注意参数的名字是固定的,不能灵活改变。 传参的…...

数字乡村创新实践探索:科技赋能农业现代化与乡村治理体系现代化同步推进
随着信息技术的飞速发展,数字乡村作为乡村振兴的重要战略方向,正日益成为推动农业现代化和乡村治理体系现代化的关键力量。科技赋能下的数字乡村,不仅提高了农业生产的效率和品质,也为乡村治理带来了新的机遇和挑战。本文旨在探讨…...

C语言——找单身狗1
题目描述: 在一个整形数组中,只有一个数字出现一次,其他数组都是成对出现的,找出那个只出现一次的数字。 例如: 数组中:1,2,3,4,5,4,3…...

Day82:服务攻防-开发组件安全Solr搜索Shiro身份Log4j日志本地CVE环境复现
目录 J2EE-组件Solr-本地demo&CVE 命令执行(CVE-2019-17558) 远程命令执行漏洞(CVE-2019-0193) Apache Solr 文件读取&SSRF (CVE-2021-27905) J2EE-组件Shiro-本地demo&CVE CVE_2016_4437 Shiro-550Shiro-721(RCE) CVE-2020-11989(身…...
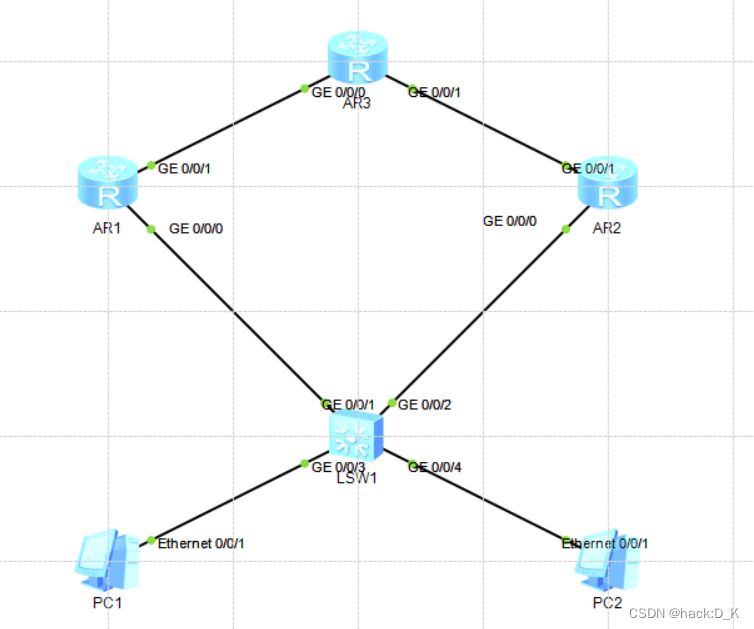
网络协议——VRRP(虚拟路由冗余协议)原理与配置
1. VRRP概述 单网关出现故障后下联业务中断,配置两个及以上的网关时由于IP地址冲突,导致通讯时断时续甚至通信中断。VRRP组播类的网络层协议 2. 协议版本 VRRP v2: 支持认证,仅适用于IPv4网络 VRRP v3: 不支持认证, 适用于IPv4和IPv6两种网…...
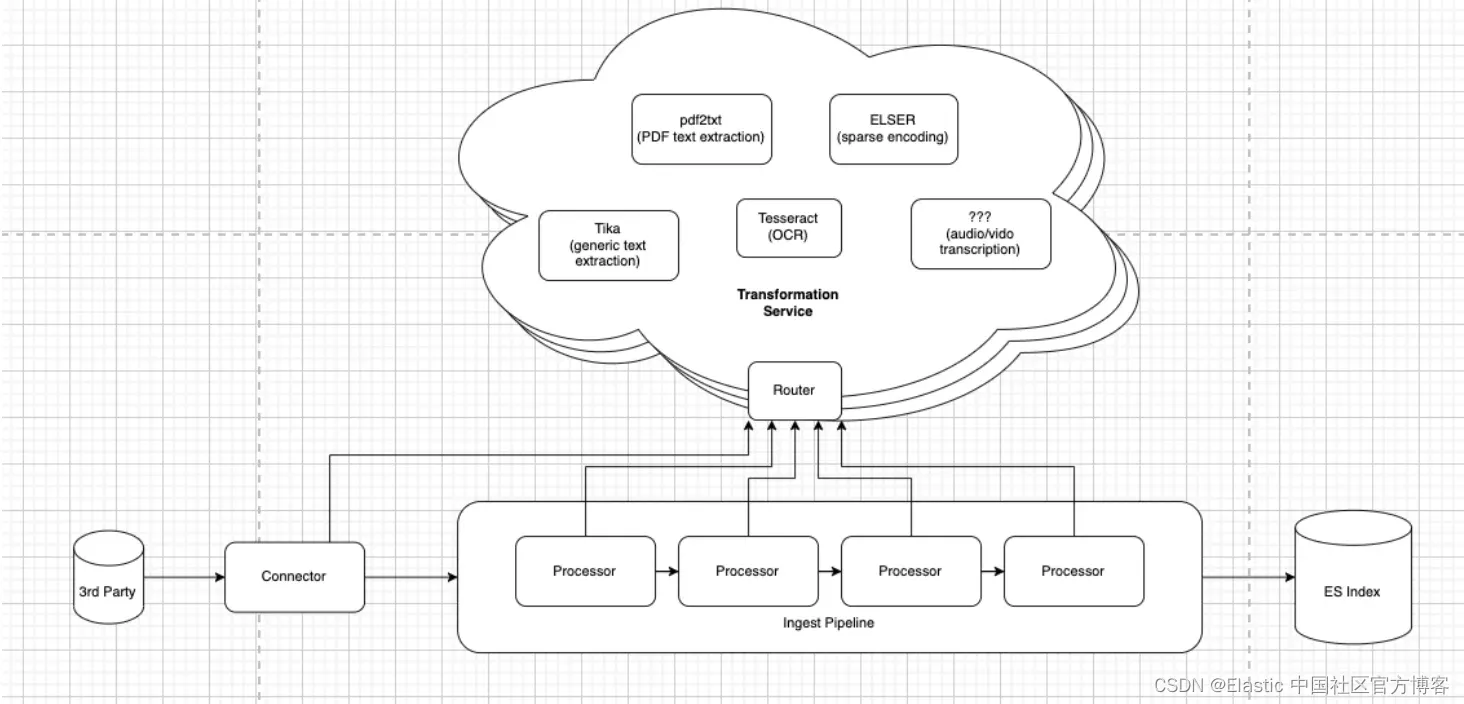
Elasticsearch:我们如何演化处理二进制文档格式
作者:来自 Elastic Sean Story 从二进制文件中提取内容是一个常见的用例。一些 PDF 文件可能非常庞大 — 考虑到几 GB 甚至更多。Elastic 在处理此类文档方面已经取得了长足的进步,今天,我们很高兴地介绍我们的新工具 —— 数据提取服务&…...
第八讲 Sort Aggregate 算法
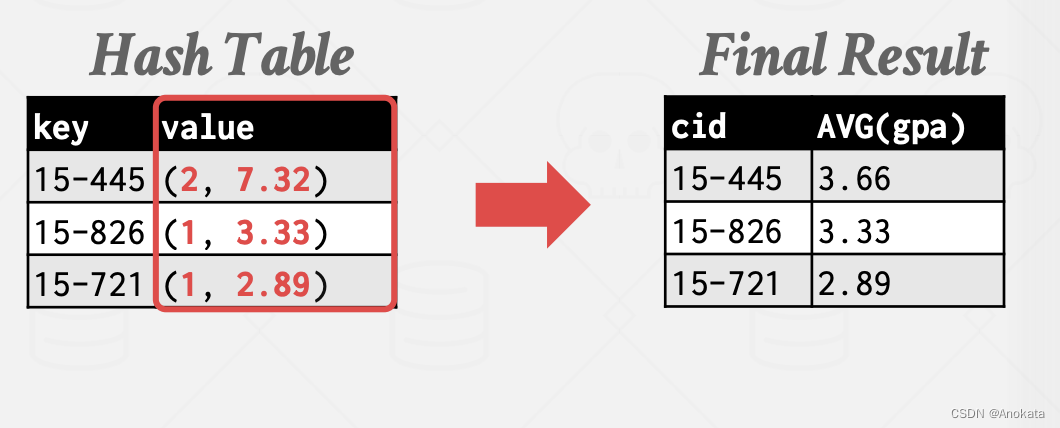
我们现在将讨论如何使用迄今为止讨论过的 DBMS 组件来执行查询。 1 查询计划【Query Plan】 我们首先来看当一个查询【Query】被解析【Parsed】后会发生什么? 当 SQL 查询被提供给数据库执行引擎,它将通过语法解析器进行检查,然后它会被转换…...
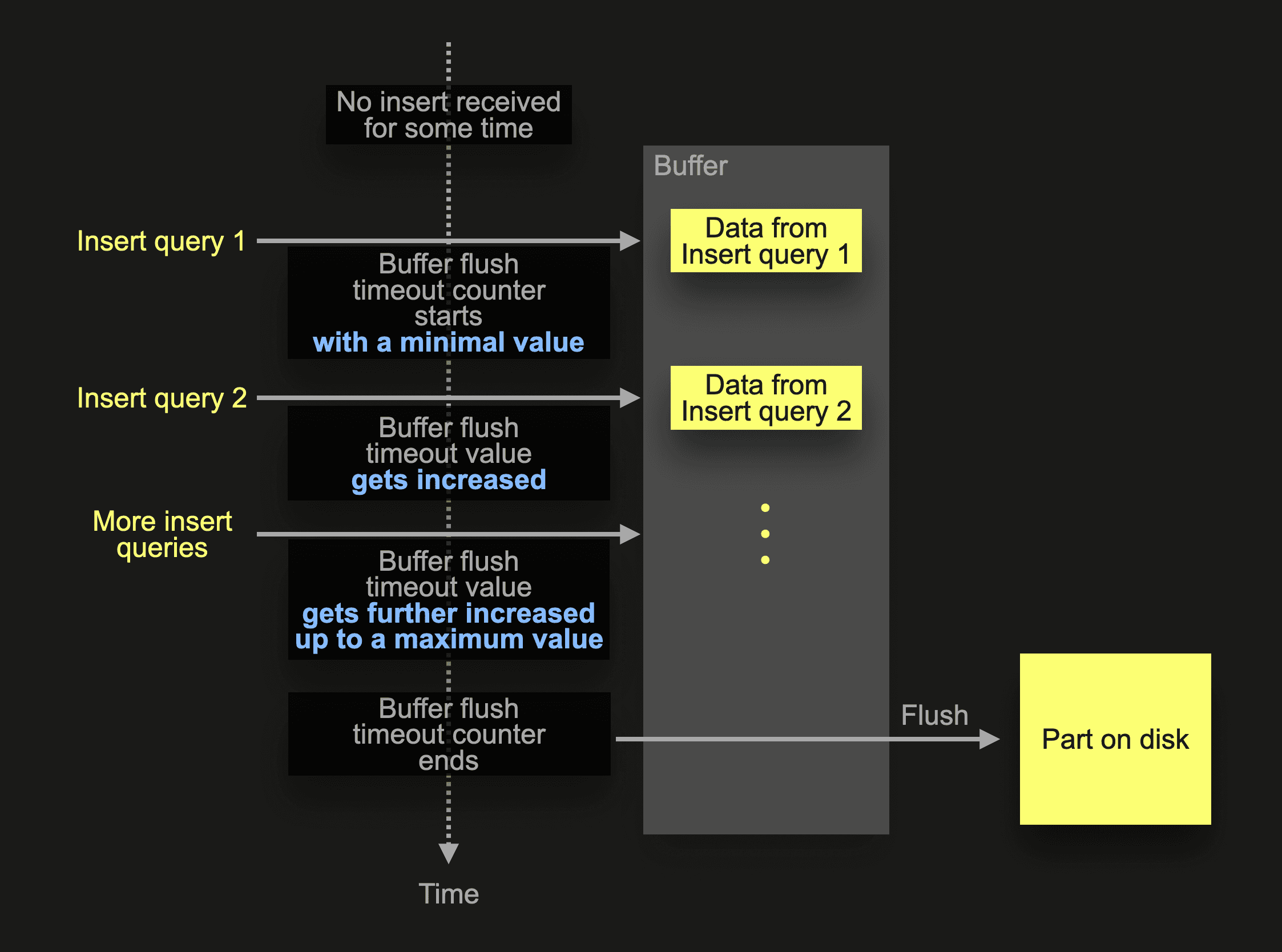
clickhouse MPPDB数据库--新特性使用示例
clickhouse 新特性: 从clickhouse 22.3至最新的版本24.3.2.23,clickhouse在快速发展中,每个版本都增加了一些新的特性,在数据写入、查询方面都有性能加速。 本文根据clickhouse blog中的clickhouse release blog中,学…...
MATLAB多级分组绘图及图例等细节处理 ; MATLAB画图横轴时间纵轴数值按照不同sensorCode分组画不同sensorCode的曲线
平时研究需要大量的绘图Excel有时候又臃肿且麻烦 尤其是当处理大量数据时可能会拖死Windows 示例代码及数据量展示 因为数据量是万级别的折线图也变成"柱状图"了, 不过还能看出大致趋势! 横轴是时间纵轴是传感器数值图例是传感器所在深度 % data readtable(C:\U…...

20240405,数据类型,运算符,程序流程结构
是我深夜爆炸,不能再去补救C了,真的来不及了,不能再三天打鱼两天晒网了,真的来不及了呜呜呜呜 我实在是不知道看什么课,那黑马吧……MOOC的北邮的C正在进行呜呜 #include <iostream> using namespace std; int…...
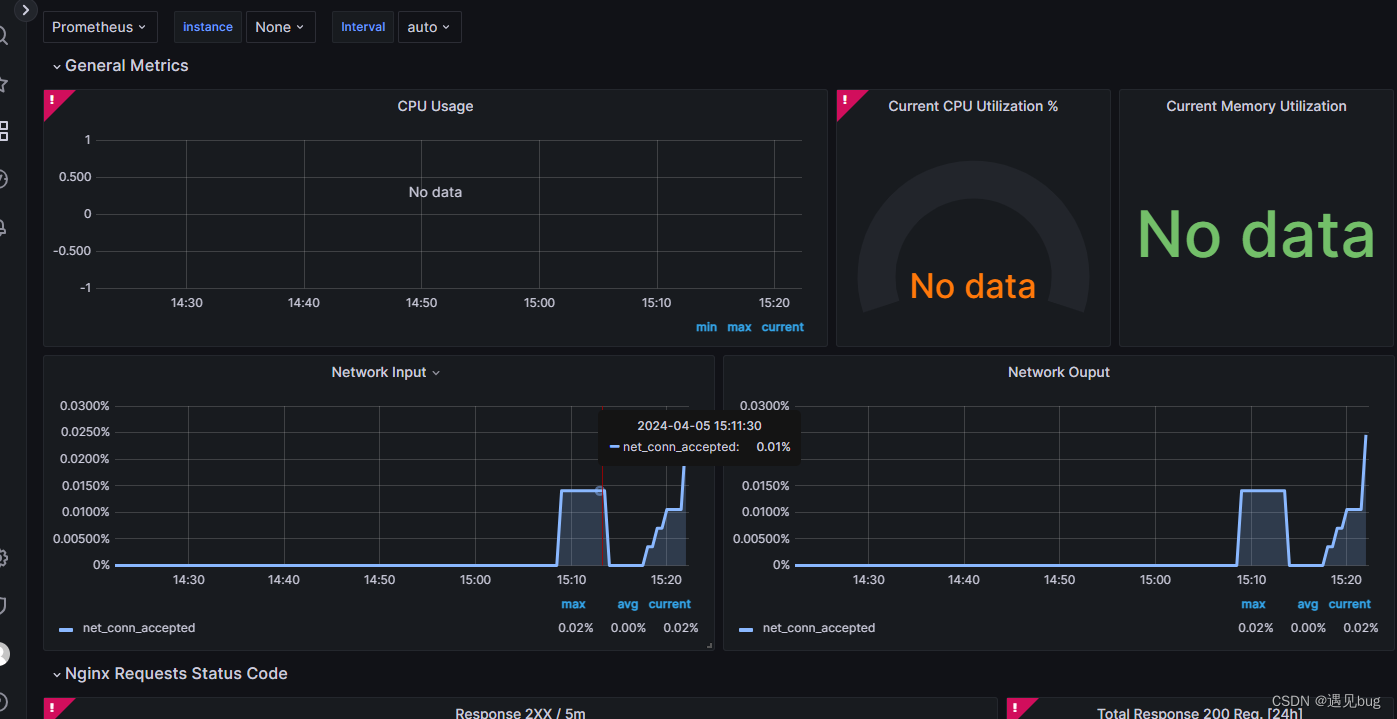
Prometheus+grafana环境搭建Nginx(docker+二进制两种方式安装)(六)
由于所有组件写一篇幅过长,所以每个组件分一篇方便查看,前五篇链接如下 Prometheusgrafana环境搭建方法及流程两种方式(docker和源码包)(一)-CSDN博客 Prometheusgrafana环境搭建rabbitmq(docker二进制两种方式安装)(二)-CSDN博客 Prometheusgrafana环…...

贝叶斯逻辑回归
贝叶斯逻辑回归(Bayesian Logistic Regression)是一种机器学习算法,用于解决分类问题。它基于贝叶斯定理,通过建立一个逻辑回归模型,结合先验概率和后验概率,对数据进行分类。 贝叶斯逻辑回归的基本原理是…...

Win10 下 Vision Mamba(Vim-main)的环境配置(libcuda.so文件无法找到,windows系统运行失败)
目录 1、下载NVIDIA 驱动程序、cuda11.8、cudnn8.6.0 2、在Anaconda中创建环境并激活 3、下载gpu版本的torch 4、配置环境所需要的包 5、安装causal_conv1d和mamba-1p1p1 安装causal_conv1d 安装mamba-1p1p1 6、运行main.py失败 请直接拉到最后查看运行失败的原因&am…...

4 万字全面掌握数据库、数据仓库、数据集市、数据湖、数据中台
如今,随着诸如互联网以及物联网等技术的不断发展,越来越多的数据被生产出来-据统计,每天大约有超过2.5亿亿字节的各种各样数据产生。这些数据需要被存储起来并且能够被方便的分析和利用。 随着大数据技术的不断更新和迭代,数据管…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
