数据结构(六)——图的应用
6.4 图的应用
6.4.1 最小生成树
对于⼀个带权连通⽆向图G = (V, E),⽣成树不同,每棵树的权(即树中所有边上的权值之和)也可能不同。设R为G的所有⽣成树的集合,若T为R中边的权值之和最小的生成树,则T称为G的最小生成树(Minimum-Spanning-Tree, MST)。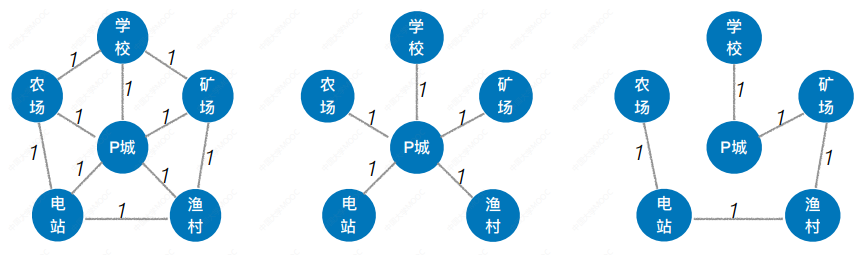
最小生成树可能有多个,但边的权值之和总是唯一且最小的
最小生成树的边数=顶点数–1。砍掉一条则不连通,增加一条边则会出现回路
求最小生成树
Prim算法(普里姆):
从某一个顶点开始构建生成树;
每次将代价最小的新顶点纳入生成树,
直到所有顶点都纳入为止。
Kruskal算法(克鲁斯卡尔):
每次选择一条权值最小的边,使这条边的两头连通(原本已经连通的就不选)
直到所有结点都连通

Prim算法的实现思想
第1轮:循环遍历所有个结点,找到lowCost最低的,且还没加入树的顶点
第2轮︰循环遍历所有个结点,找到lowCost最低的,且还没加入树的顶点
第3轮:循环遍历所有个结点,找到lowCost最低的,且还没加入树的顶点
第4轮:循环遍历所有个结点,找到lowCost最低的,且还没加入树的顶点
第5轮:循环遍历所有个结点,找 到lowCost最低的,且还没加入树的顶点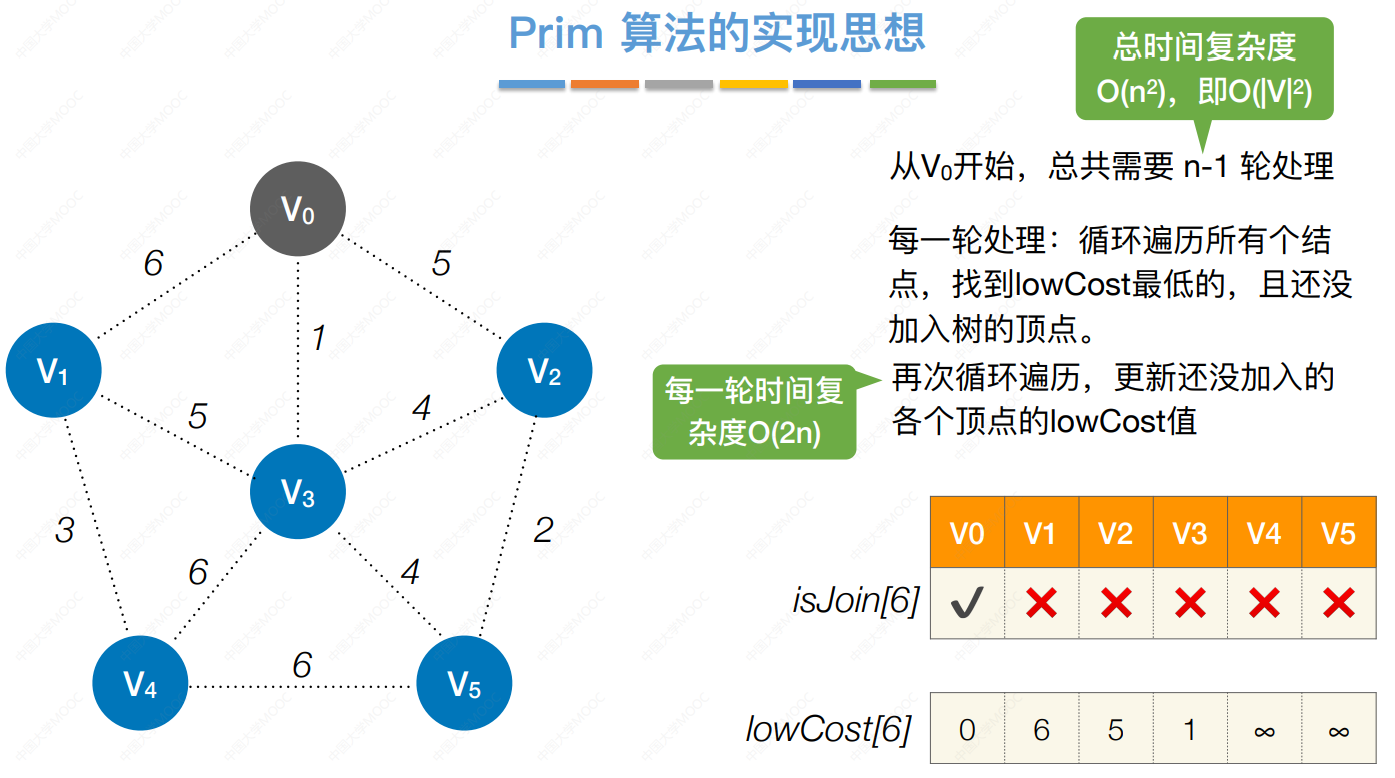
Kruskal 算法的实现思想
第1轮:检查第1条边的两个顶点是否 连通(是否属于同⼀个集合)
第2轮:检查第2条边的两个顶点是否 连通(是否属于同⼀个集合)
第3轮:检查第3条边的两个顶点是否 连通(是否属于同⼀个集合)
第4轮:检查第4条边的两个顶点是否 连通(是否属于同⼀个集合)
第5轮:检查第5条边的两个顶点是否 连通(是否属于同⼀个集合)
第6轮:检查第6条边的两个顶点是否 连通(是否属于同⼀个集合)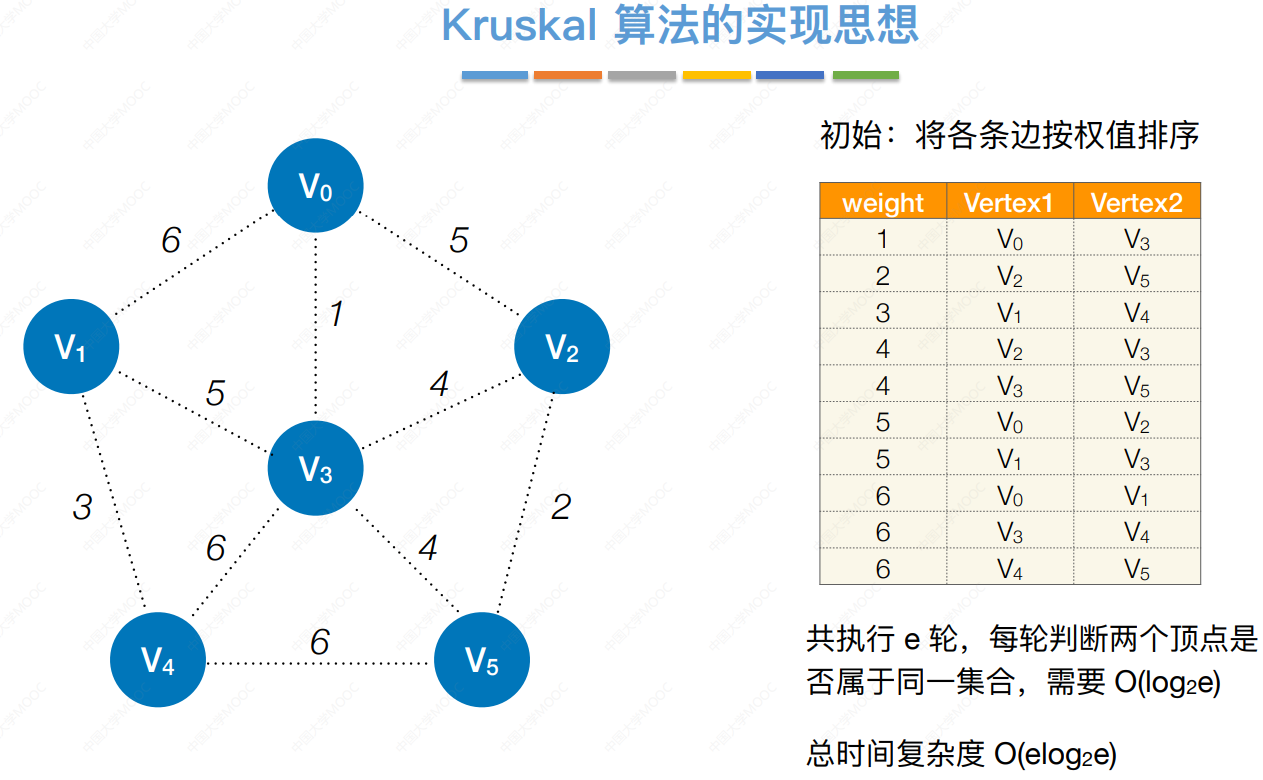

6.4.2_1 最短路径问题_BFS算法

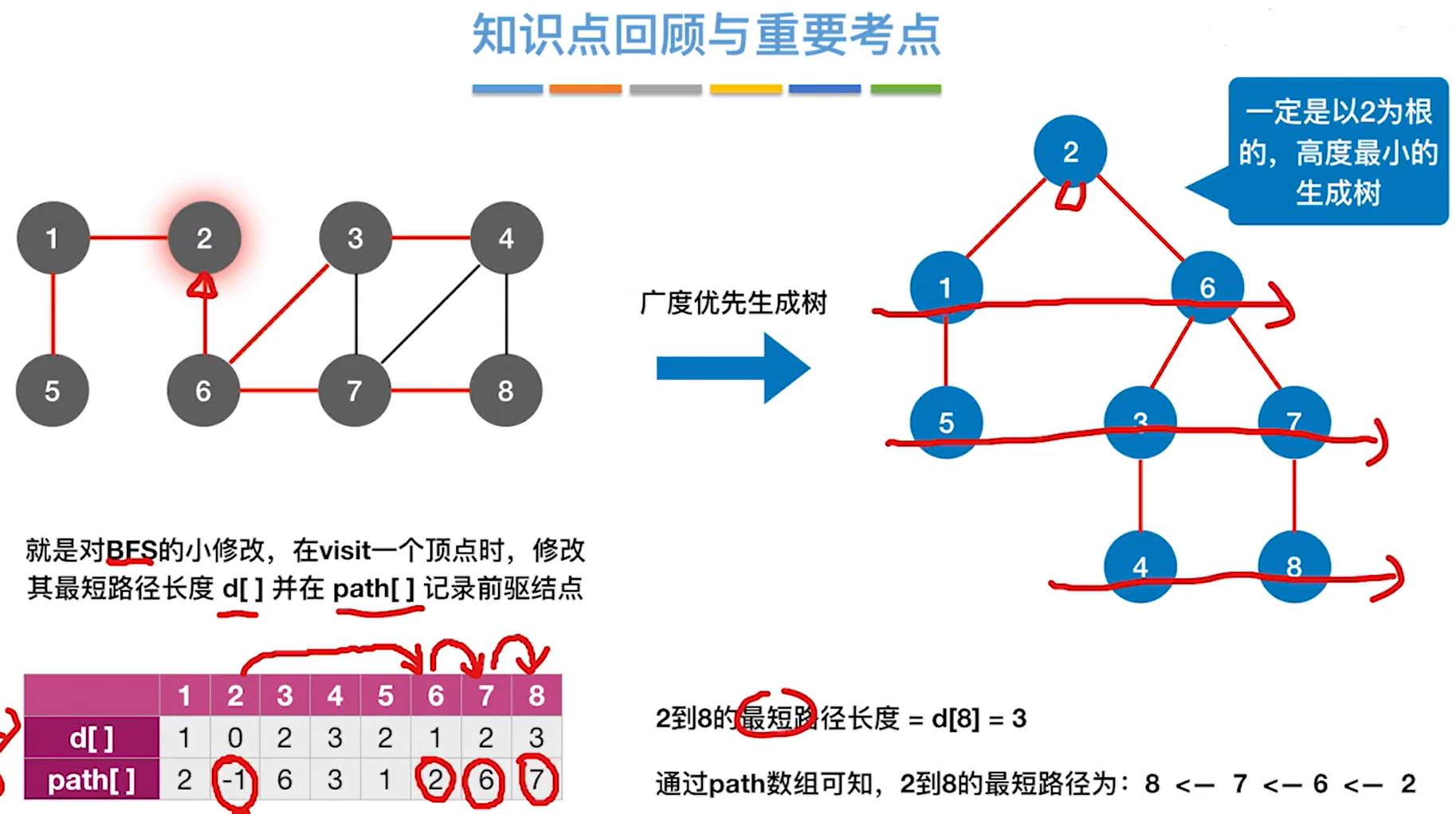
BFS求无权图的单源最短路径
#define MAX_LENGTH 2147483647 //地图中最大距离,表示正无穷//求顶点u到其他顶点的最短路径
void BFS_MIN_Disrance(Graph G,int u){//d[i]表示从u到i结点的最短路径for(i=0; i<G.vexnum; i++){visited[i]=FALSE; //初始化访问标记数组d[i]=MAX_LENGTH; //初始化路径长度path[i]=-1; //初始化最短路径记录}InitQueue(Q); //初始化辅助队列d[u]=0;visites[u]=TREE;EnQueue(Q,u);while(!isEmpty[Q]){ //BFS算法主过程DeQueue(Q,u); //队头元素出队并赋给ufor(w=FirstNeighbor(G,u);w>=0;w=NextNeighbor(G,u,w)){if(!visited[w]){ //w为u的尚未访问的邻接顶点d[w]=d[u]+1; //路径长度+1path[w]=u; //最短路径应从u到wvisited[w]=TREE; //设已访问标记EnQueue(Q,w); //顶点w入队}}}
}
6.4.2_2 最短路径问题_Dijkstra算法

使用 Dijkstra算法求最短路径问题,需要使用三个数组:
final[]数组用于标记各顶点是否已找到最短路径。
dist[]数组用于记录各顶点到源顶点的最短路径长度。
path[]数组用于记录各顶点现在最短路径上的前驱。
算法思想:循环遍历所有结点,找到还没确定最短路径、且dist最小的顶点Vi,令final[i]=ture。
检查所有邻接自Vi的顶点,若其final值为false,则更新dist和path信息。
#define MAX_LENGTH = 2147483647;// 求顶点u到其他顶点的最短路径
void BFS_MIN_Disrance(Graph G,int u){for(int i=0; i<G.vexnum; i++){ //初始化数组final[i]=FALSE;dist[i]=G.edge[u][i];if(G.edge[u][i]==MAX_LENGTH || G.edge[u][i] == 0)path[i]=-1;elsepath[i]=u;final[u]=TREE;}for(int i=0; i<G.vexnum; i++){int MIN=MAX_LENGTH;int v;// 循环遍历所有结点,找到还没确定最短路径,且dist最⼩的顶点vfor(int j=0; j<G.vexnum; j++){if(final[j]!=TREE && dist[j]<MIN){MIN = dist[j];v = j;}}final[v]=TREE;// 检查所有邻接⾃v的顶点路径长度是否最短for(int j=0; j<G.vexnum; j++){if(final[j]!=TREE && dist[j]>dist[v]+G.edge[v][j]){dist[j] = dist[v]+G.edge[v][j];path[j] = v;}}}
}

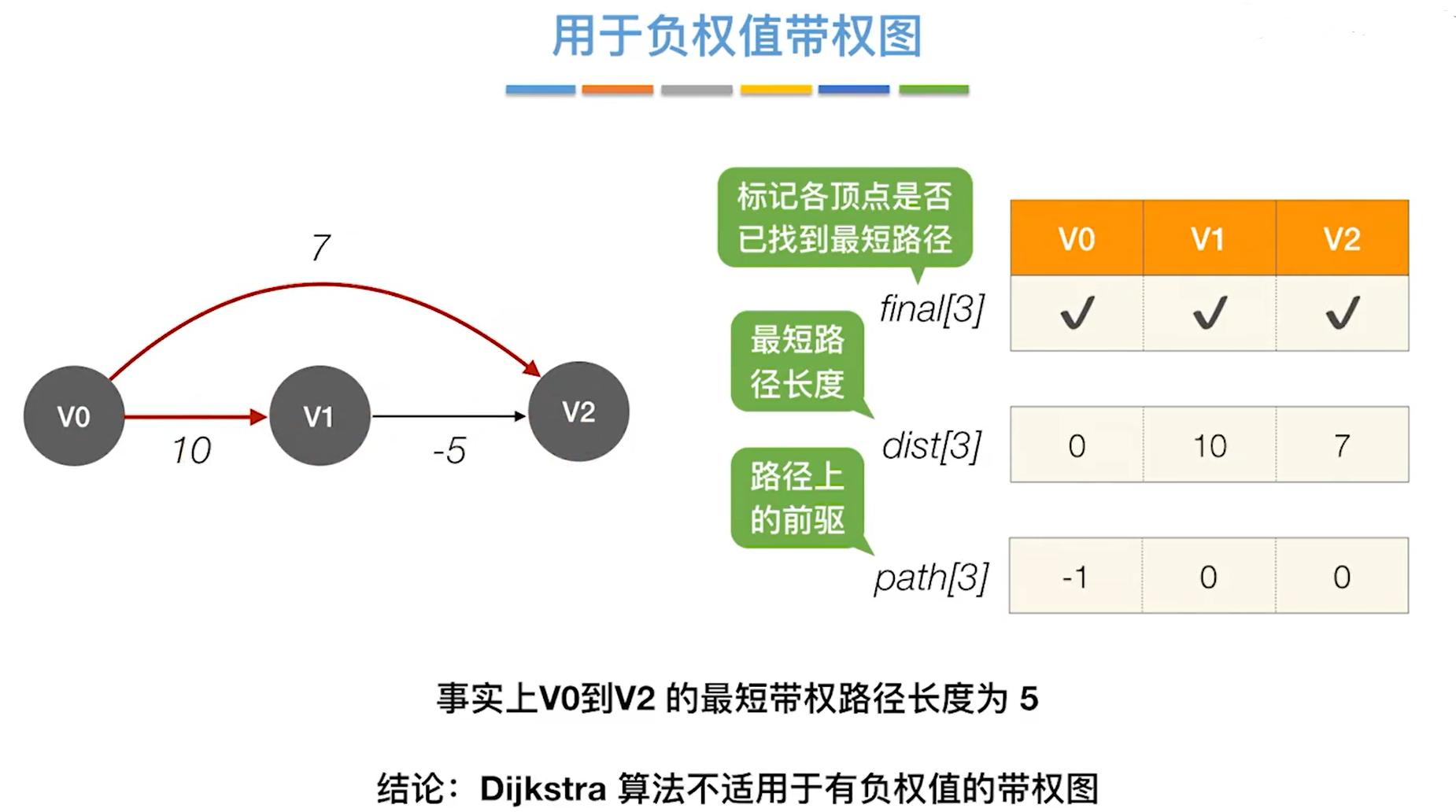
Dijkstra算法能够很好的处理带权图的单源最短路径问题,但不适⽤于有负权值的带权图。
6.4.2_3 最短路径问题_Floyd算法
Floyd算法:求出每⼀对顶点之间的最短路径,使⽤动态规划思想,将问题的求解分为多个阶段。
Floyd算法使用到两个矩阵:
dist[]:目前各顶点间的最短路径。
path[]:两个顶点之间的中转点。
//...准备工作,根据图的信息初始化矩阵A和pathfor(k=0;k<n;k++){ //考虑以Vk作为中转点for(i=0;i<n;i++){ //遍历整个矩阵,i为行号,j为列号for(j=0;j<n;j++){if(A[i][j]>A[i][k]+A[k][j]){ //以Vk为中转地按的路径更短A[i][j]=A[i][k]+A[k][j]; //更新最短路径长度path[i][j]=k; //中转点}}}}

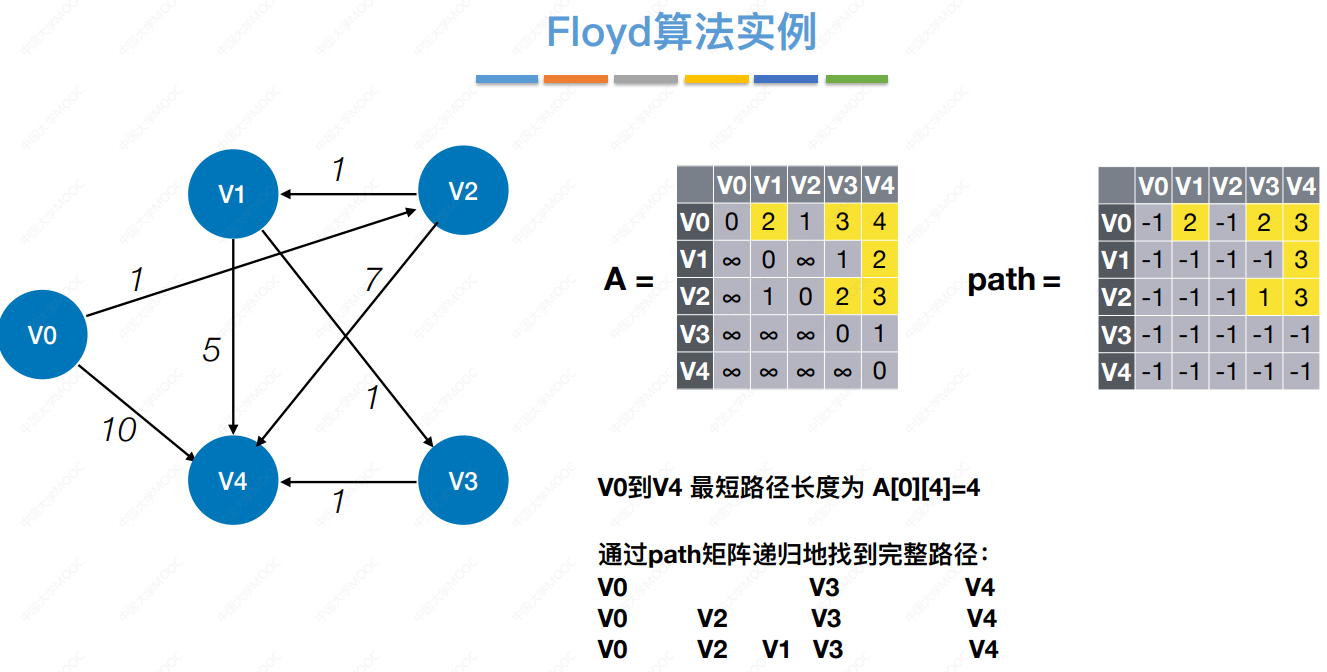

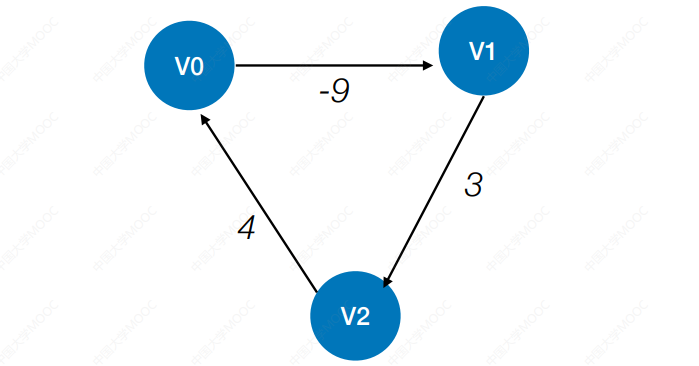
Floyd算法不能解决带有“负权回路”的图(有负权值的边组成回路),这种图有可能没有最短路径
最短路径算法比较:
| BFS算法 | Dijkstra算法 | Floyd算法 | |
| 无权图 | ✔ | ✔ | ✔ |
| 带权图 | ✘ | ✔ | ✔ |
| 带负权值的图 | ✘ | ✘ | ✔ |
| 带负权回路的图 | ✘ | ✘ | ✘ |
| 时间复杂度 | O(|V|^2)或O(|V|+|E|) | O(|V|^2) | O(|V|^3) |
| 通常用于 | 求无权图的单源最短路径 | 求带权图的单源最短路径 | 求带权图中各顶点间的最短路径 |
6.4.3 有向无环图描述表达式
有向无环图:若一个有向图中不存在环,则称为有向无环图,简称DAG图(Directed Acyclic Graph)

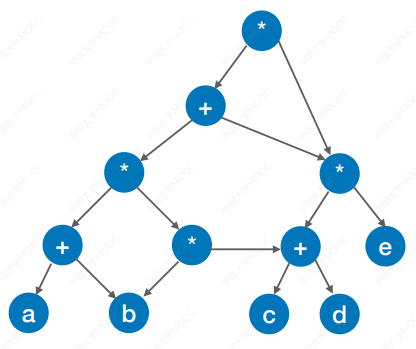

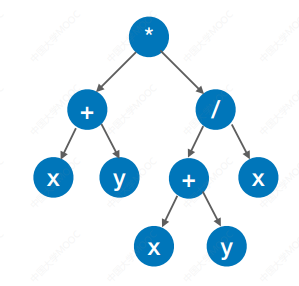

解题方法
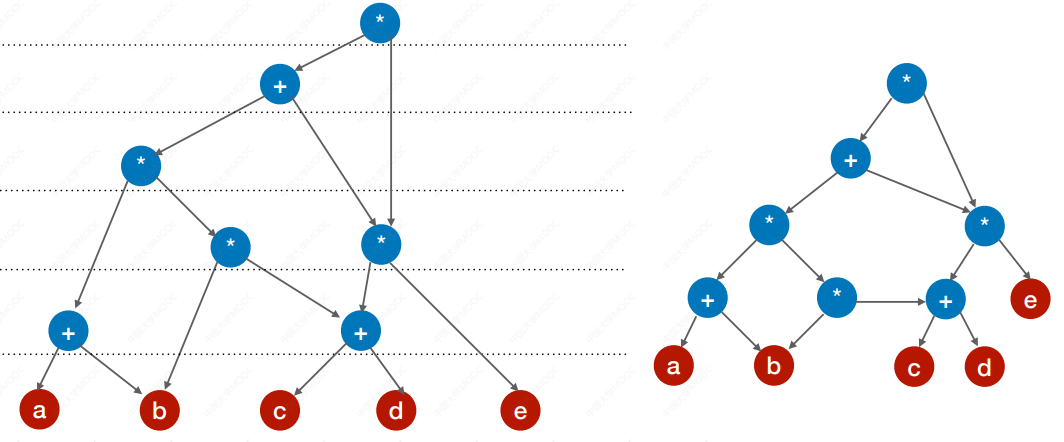
练习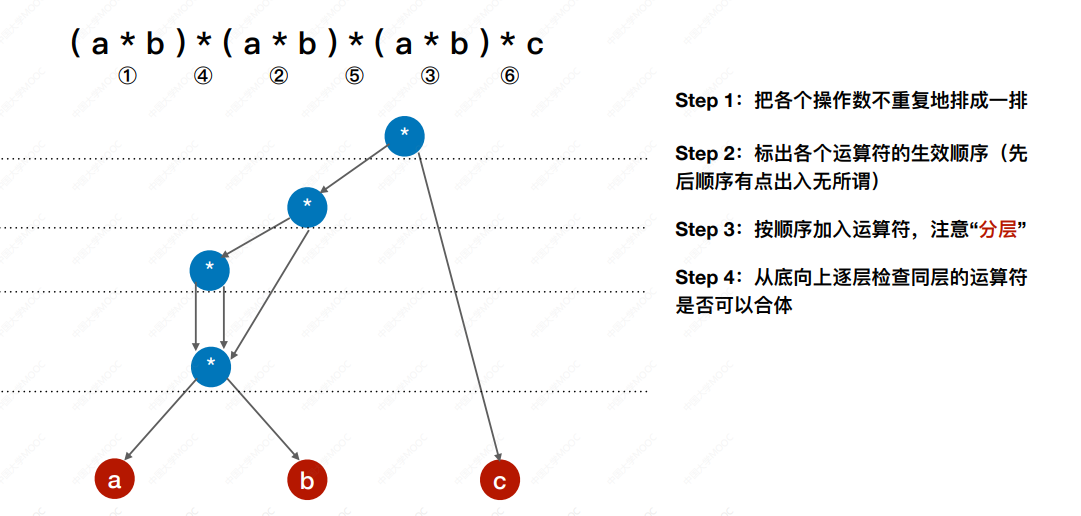
6.4.4 拓扑排序
AOV网(Activity on vertex Network,用顶点表示活动的网):
用DAG图(有向无环图)表示一个工程。顶点表示活动,有向边<Vi,Vj>表示活动Vi必须先于活动Vj进行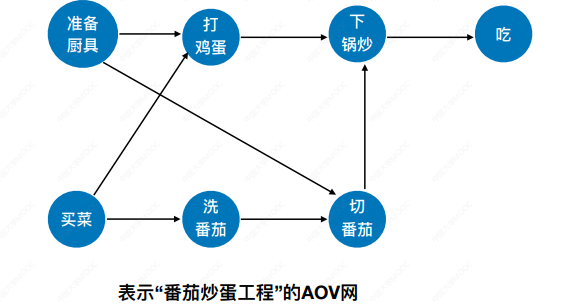
拓扑排序︰在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,称为该图的一个拓扑排序:
①每个顶点出现且只出现一次。
②若顶点A在序列中排在顶点B的前面,则在图中不存在从顶点B到顶点A的路径。
或定义为:拓扑排序是对有向无环图的顶点的一种排序,它使得若存在一条从顶点A到顶点B的路径,则在排序中顶点B出现在顶点A的后面。每个AOV网都有一个或多个拓扑排序序列。
拓扑排序的实现:
① 从AOV网中选择⼀个没有前驱(入度为0)的顶点并输出。
② 从网中删除该顶点和所有以它为起点的有向边。
③ 重复①和②直到当前的AOV网为空或当前网中不存在无前驱的顶点为止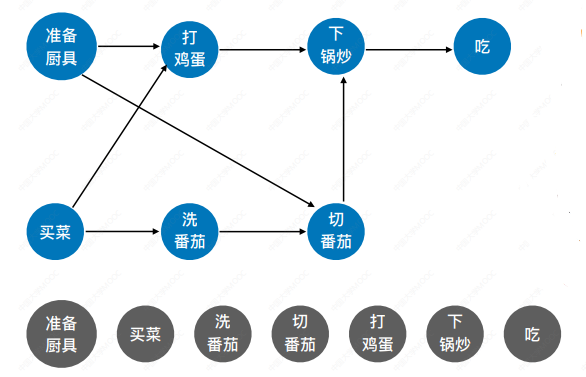
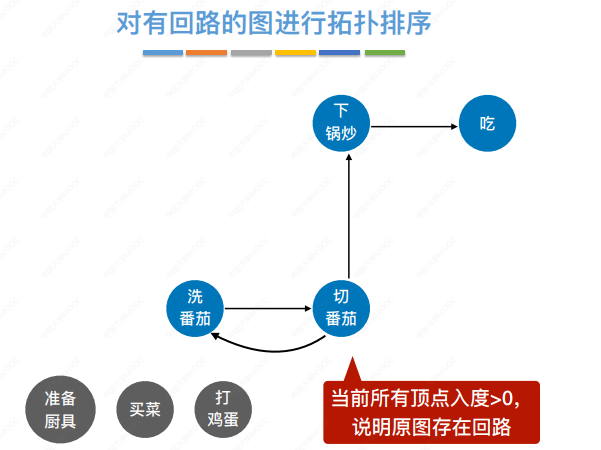
代码实现拓扑排序
#define MaxVertexNum 100 //图中顶点数目最大值typedef struct ArcNode{ //边表结点int adjvex; //该弧所指向的顶点位置struct ArcNode *nextarc; //指向下一条弧的指针
}ArcNode;typedef struct VNode{ //顶点表结点VertexType data; //顶点信息ArcNode *firstarc; //指向第一条依附该顶点的弧的指针
}VNode,AdjList[MaxVertexNum];typedef struct{AdjList vertices; //邻接表int vexnum,arcnum; //图的顶点数和弧数
}Graph; //Graph是以邻接表存储的图类型// 对图G进行拓扑排序
bool TopologicalSort(Graph G){InitStack(S); //初始化栈,存储入度为0的顶点for(int i=0;i<g.vexnum;i++){if(indegree[i]==0)Push(S,i); //将所有入度为0的顶点进栈}int count=0; //计数,记录当前已经输出的顶点数while(!IsEmpty(S)){ //栈不空,则存入Pop(S,i); //栈顶元素出栈print[count++]=i; //输出顶点ifor(p=G.vertices[i].firstarc;p;p=p=->nextarc){//将所有i指向的顶点的入度减1,并将入度为0的顶点压入栈v=p->adjvex;if(!(--indegree[v]))Push(S,v); //入度为0,则入栈}}if(count<G.vexnum)return false; //排序失败,有向图中有回路elsereturn true; //拓扑排序成功
}
拓扑排序 每个顶点都需要处理一次 每条边都需要处理一次
时间复杂度:O(|V|+|E|)
若采用邻接矩阵,则需O(|V^2|)
逆拓扑排序
对一个AOV网,如果采用下列步骤进行排序,则称之为逆拓扑排序:
①从AOV网中选择一个没有后继(出度为O)的顶点并输出。
②从网中删除该顶点和所有以它为终点的有向边。
③重复①和②直到当前的AOV网为空。
逆拓扑排序的实现(DFS算法)
void DFSTraverse(Graph G){ //对图G进行深度优先遍历for(v=0; v<G.vexnum;++V)visited[v]=FALSE; //初始化已访问标记数据for(v=;v<G.vexnum; ++V) //本代码中是从v=0开始遍历if(!visited[v])DFS(G,v);
}void DFS(Graph G,int v){ //从顶点v出发,深度优先遍历图Gvisited [v]=TRUE; //设已访问标记for(w=FirstNeighbor(G,v);w>=0 ; w=NextNeighor(G,v,w))if(!visited[w]){ //w为u的尚未访问的邻接顶点DFS(G,w);}//ifprint(v); //输出顶点
}
6.4.5 关键路径
AOE 网:在带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销(如完成活动所需的时间),称之为用边表示活动的网络,简称 AOE 网 (Activity On Edge NetWork)。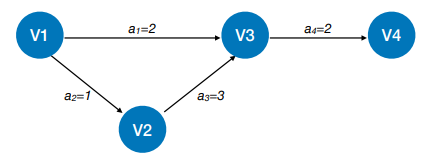
AOE网具有以下两个性质:
①只有在某顶点所代表的事件发⽣后,从该顶点出发的各有向边所代表的活动才能开始;
②只有在进⼊某顶点的各有向边所代表的活动都已结束时,该顶点所代表的事件才能发⽣。
在 AOE 网中仅有⼀个入度为 0 的顶点,称为开始顶点(源点),它表示整个⼯程的开始; 也仅有⼀个出度为 0 的顶点,称为结束顶点(汇点),它表示整个⼯程的结束。
在AOE网中,有些活动是可以并行进行的。从源点到汇点的有向路径可能有多条,所有路径中,具有最大路径长度的路径称为关键路径,而把关键路径上的活动称为关键活动。完成整个工程的最短时间就是关键路径的长度,若关键活动不能按时完成,则整个工程的完成时间就会延长。
寻找冠军活动时所用到的几个参量的定义:
1. 事件 vk的最早发生时间 ve(k):决定了所有从vk 开始的活动能够开工的最早时间。
2. 事件 vk的最迟发⽣时间 vl(k):它是指在不推迟整个工程完成的前提下,该事件最迟必须发⽣的时间。
3.活动ai的最早开始时间e(i):指该活动弧的起点所表示的事件的最早发生时间。
4.活动ai的最迟开始时间l(i):它是指该活动弧的终点所表示事件的最迟发生时间与该活动所需时间之差。
5.活动 ai的时间余量d(i)=l(i)−e(i),表示在不增加完成整个⼯程所需总时间的情况下,活动ai可以拖延的时间若⼀个活动的时间余量为零,则说明该活动必须要如期完成,d(i)=0 即l(i)=e(i) 的活动ai是关键活动,由关键活动组成的路径就是关键路径。
求关键路径的步骤:
1.求所有事件的最早发生时间ve():按拓扑排序序列,依次求各个顶点的ve(k), ve(源点)=0, ve(k) =Max{vef)+W eight(vj , vk )},vj为vk的任意前驱。
2.求所有事件的最迟发生时间vl():按逆拓扑排序序列,依次求各个顶点的 vl(k),vl(汇点)= ve(汇点),vl(k)=Min{vl(j)- W eight(vk , vi)},v为Vv\k 的任意后继。
3.求所有活动的最早发生时间e():若边<Vk ,Vj>表示活动a;,则有e(i)=ve(k)。
4.求所有活动的最迟发生时间1():若边<Vk,Vj >表示活动a,则有l(i)= vl(j)- Weight(vi , vj)。
5.求所有活动的时间余量d(): d(i)= l(i)-e(i)。
关键活动、关键路径的特性:
1.若关键活动耗时增加,则整个工程的工期将增长。
2.缩短关键活动的时间,可以缩短整个工程的工期。
3.当缩短到一定程度时,关键活动可能会变成非关键活动。
4.可能有多条关键路径,只提高一条关键路径上的关键活动速度并不能缩短整个工程的工期,只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。
相关文章:

数据结构(六)——图的应用
6.4 图的应用 6.4.1 最小生成树 对于⼀个带权连通⽆向图G (V, E),⽣成树不同,每棵树的权(即树中所有边上的权值之和)也可能不同。设R为G的所有⽣成树的集合,若T为R中边的权值之和最小的生成树,则T称为G的…...
java自动化测试学习-03-06java基础之运算符
运算符 算术运算符 运算符含义举例加法,运算符两侧的值相加ab等于10-减法,运算符左侧减右侧的值a-b等于6*乘法,运算符左侧的值乘以右侧的值a*b等于16/除法,运算符左侧的值除以右侧的值a/b等于4%取余,运算符左侧的值除…...
【VASP学习】在Ubuntu系统安装vasp.5.4.4的全过程(包括VASP官方学习资料、安装过程中相关编辑器的配置、VASP的编译及VASP的测试)
在Ubuntu系统安装vasp.5.4.4的全过程 VASP的简介与相关学习资料安装前的准备工作及说明安装过程intel编译器的安装VASP的编译VASP的测试 参考来源 VASP的简介与相关学习资料 VASP(Vienna Ab initio Simulation Package)是基于第一性原理对原子尺度的材料进行模拟计算的软件。比…...
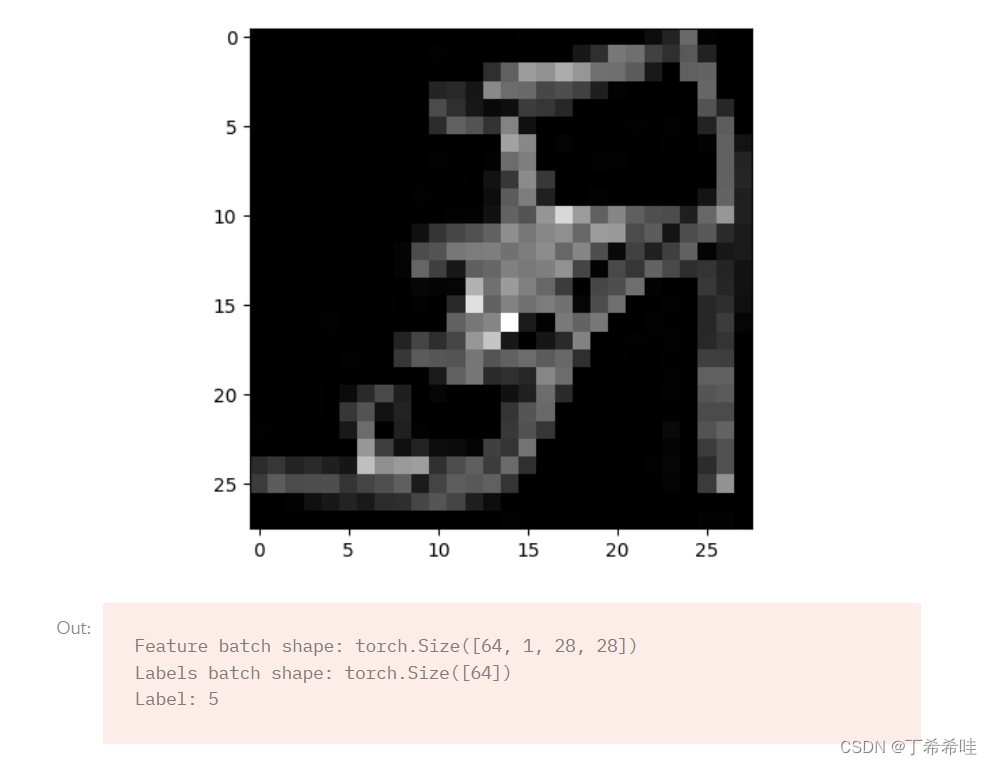
PyTorch|Dataset与DataLoader使用、构建自定义数据集
文章目录 一、Dataset与DataLoader二、自定义Dataset类(一)\_\_init\_\_函数(二)\_\_len\_\_函数(三)\_\_getitem\_\函数(四)全部代码 三、将单个样本组成minibatch(Data…...
4.6(信息差)
🌍 山西500千伏及以上输电线路工程首次采用无人机AI自主验收 🌋 中国与泰国将开展国际月球科研站等航天合作 ✨ 网页版微软 PowerPoint 新特性:可直接修剪视频 🍎 特斯拉开始在德国超级工厂生产出口到印度的右舵车 1.马斯克&…...

关于C#操作SQLite数据库的一些函数封装
主要功能:增删改查、自定义SQL执行、批量执行(事务)、防SQL注入、异常处理 1.NuGet中安装System.Data.SQLite 2.SQLiteHelper的封装: using System; using System.Collections.Generic; using System.Data.SQLite; using System.…...

LeetCode-79. 单词搜索【数组 字符串 回溯 矩阵】
LeetCode-79. 单词搜索【数组 字符串 回溯 矩阵】 题目描述:解题思路一:回溯 回溯三部曲。这里比较关键的是给board做标记,防止之后搜索时重复访问。解题思路二:回溯算法 dfs,直接看代码,很容易理解。visited哈希,防止…...
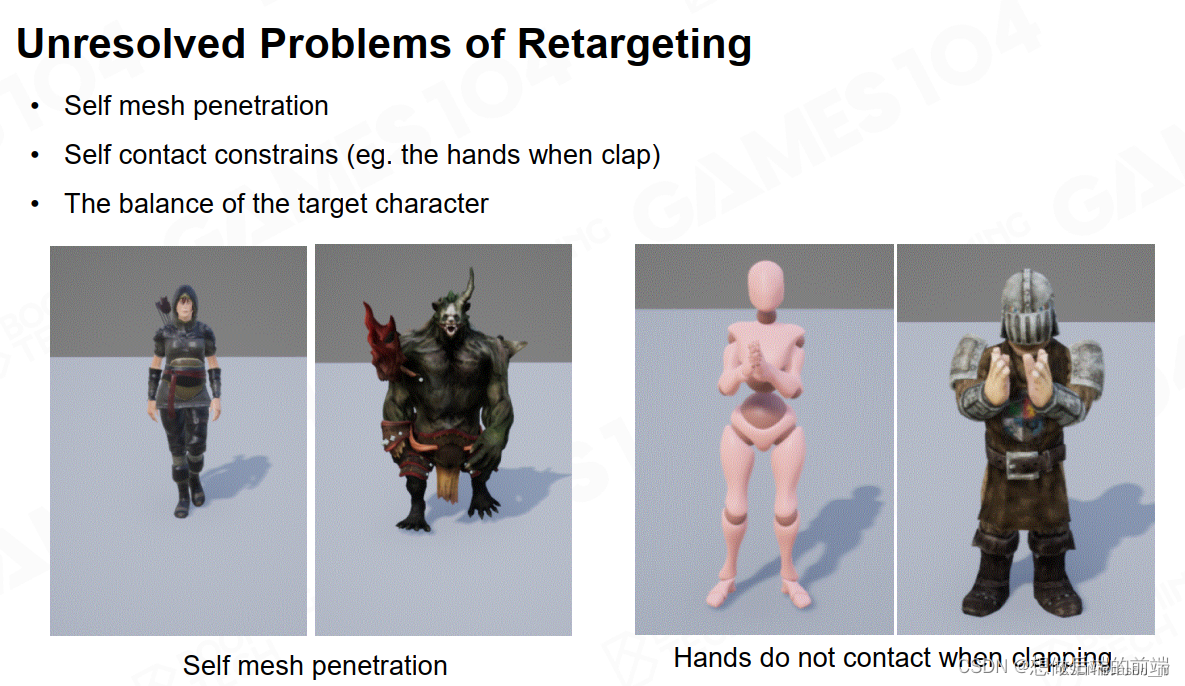
游戏引擎之高级动画技术
一、动画混合 当我们拥有各类动画素材(clips)时,要将它们融合起来成为一套完整的动画。 最经典的例子就是从走的动画自然的过渡到跑的动画。 1.1 线性插值 不同于上节课的LERP(同一个clip内不同pose之间)ÿ…...
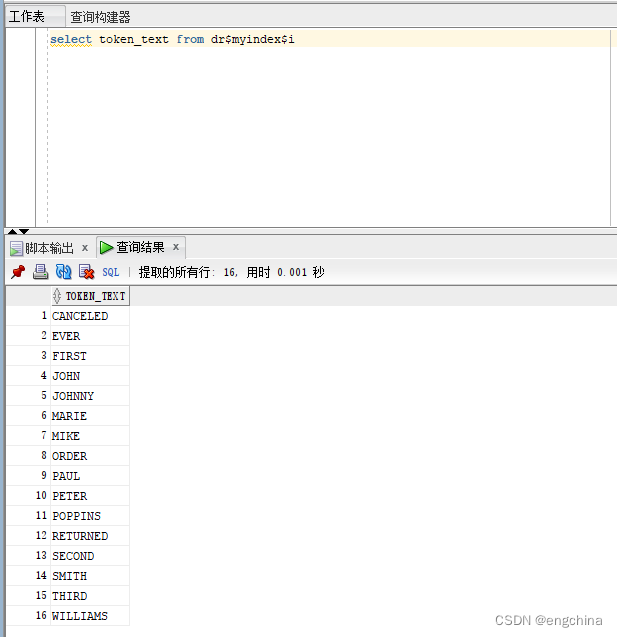
Oracle 数据库中的全文搜索
Oracle 数据库中的全文搜索 0. 引言1. 整体流程2. 创建索引2-1. 创建一个简单的表2-2. 创建文本索引2-3. 查看创建的基础表 3. 运行查询3-1. 运行文本查询3-2. CONTAINS 运算符3-3. 混合查询3-4. OR 查询3-5. 通配符3-6. 短语搜索3-7. 模糊搜索(Fuzzy searches&…...

代码随想录阅读笔记-二叉树【二叉搜索树中的众数】
题目 给定一个有相同值的二叉搜索树(BST),找出 BST 中的所有众数(出现频率最高的元素)。 假定 BST 有如下定义: 结点左子树中所含结点的值小于等于当前结点的值结点右子树中所含结点的值大于等于当前结点的…...

AcWing-游戏
1388. 游戏 - AcWing题库 所需知识:博弈论,区间dp 由于双方都采取最优的策略来取数字,所以结果为确定的,有可能会有多个不同的过程,但是我们只需要关注最终结果就行了。 方法一: 定义dp[i][j] 表示区间…...

Mybatis——一对一映射
一对一映射 预置条件 在某网络购物系统中,一个用户只能拥有一个购物车,用户与购物车的关系可以设计为一对一关系 数据库表结构(唯一外键关联) 创建两个实体类和映射接口 package org.example.demo;import lombok.Data;import …...

Web 安全之 SSL 剥离攻击详解
目录 SSL/TLS简介 SSL 剥离攻击原理 SSL 剥离攻击的影响 SSL 剥离攻击的防范措施 小结 SSL 剥离攻击(SSL Stripping Attack)是一种针对安全套接层(SSL)或传输层安全性(TLS)协议的攻击手段,…...
)
数据结构——顺序表(C语言)
目录 一、顺序表概念 二、顺序表分类 1.静态顺序表 2.动态顺序表 三、顺序表的实现 1.顺序表的结构体定义 2. 顺序表初始化 3.顺序表销毁 4.顺序表的检验 5.顺序表打印 6.顺序表扩容 7.顺序表尾插与头插 8.尾删与头删 9.在pos处插入数据 10.在pos处删除数据 11.查找数据 …...
利用Idea实现Ajax登录(maven工程)
一、新建一个maven工程(不会建的小伙伴可以参考Idea引入maven工程依赖(保姆级)-CSDN博客),工程目录如图 js文件可以上up网盘提取 链接:https://pan.baidu.com/s/1yOFtiZBWGJY64fa2tM9CYg?pwd5555 提取码&…...

环信IM集成教程——Web端UIKit快速集成与消息发送
写在前面: 千呼万唤始出来,环信Web端终于出UIKit了!🎉🎉🎉 文档地址:https://doc.easemob.com/uikit/chatuikit/web/chatuikit_overview.html 环信单群聊 UIKit 是基于环信即时通讯云 IM SDK 开…...

Anaconda如何切换国内镜像源
一、anaconda如何切换阿里镜像源 在Anaconda中切换到阿里云镜像源可以通过以下步骤进行: 1、打开终端(Windows)或者命令行界面(macOS/Linux)。 2、执行以下命令来配置阿里云镜像源: conda config --add…...

Android 14.0 添加自定义服务,并生成jar给第三方app调用
1.概述 在14.0系统ROM产品定制化开发中,由于需要新增加自定义的功能,所以要增加自定义服务,而app上层通过调用自定义服务,来调用相应的功能,所以系统需要先生成jar,然后生成jar 给上层app调用,接下来就来分析实现的步骤,然后来实现相关的功能 从而来实现所需要的功能 …...

解决沁恒ch592单片机在tmos中使用USB总线时,接入USB Hub无法枚举频繁Reset的问题
开发产品时采用了沁恒ch592,做USB开发时遇到了一个奇葩的无法枚举问题。 典型症状 使用USB线直连电脑时没有问题,可以正常使用。 如果接入某些特定方案的USB Hub(例如GL3510、GL3520),可能会出现以下2种情况…...
nvm保姆级安装使用教程
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: 开发环境篇 ✨特色专栏: M…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
