代码随想录阅读笔记-二叉树【二叉搜索树中的众数】
题目
给定一个有相同值的二叉搜索树(BST),找出 BST 中的所有众数(出现频率最高的元素)。
假定 BST 有如下定义:
- 结点左子树中所含结点的值小于等于当前结点的值
- 结点右子树中所含结点的值大于等于当前结点的值
- 左子树和右子树都是二叉搜索树
例如:
给定 BST [1,null,2,2],

返回[2].
提示:如果众数超过1个,不需考虑输出顺序
进阶:你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
思路
这道题目如果不是二叉搜索树的话,应该怎么解题,是二叉搜索树,又应该如何解题,两种方式做一个比较,可以加深大家对二叉树的理解。
递归法
如果不是二叉搜索树
如果不是二叉搜索树,最直观的方法一定是把这个树都遍历了,用map统计频率,把频率排个序,最后取前面高频的元素的集合。
具体步骤如下:
1、这个树都遍历了,用map统计频率
至于用前中后序哪种遍历也不重要,因为就是要全遍历一遍,怎么个遍历法都行,层序遍历都没毛病!
这里采用前序遍历,代码如下:
// map<int, int> key:元素,value:出现频率
void searchBST(TreeNode* cur, unordered_map<int, int>& map) { // 前序遍历if (cur == NULL) return ;map[cur->val]++; // 统计元素频率searchBST(cur->left, map);searchBST(cur->right, map);return ;
}
2、把统计的出来的出现频率(即map中的value)排个序
有的同学可能可以想直接对map中的value排序,还真做不到,C++中如果使用std::map或者std::multimap可以对key排序,但不能对value排序。
所以要把map转化数组即vector,再进行排序,当然vector里面放的也是pair<int, int>类型的数据,第一个int为元素,第二个int为出现频率。
bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {return a.second > b.second; // 按照频率从大到小排序
}vector<pair<int, int>> vec(map.begin(), map.end());
sort(vec.begin(), vec.end(), cmp); // 给频率排个序
3、取前面高频的元素
此时数组vector中已经是存放着按照频率排好序的pair,那么把前面高频的元素取出来就可以了。
result.push_back(vec[0].first);
for (int i = 1; i < vec.size(); i++) {// 取最高的放到result数组中if (vec[i].second == vec[0].second) result.push_back(vec[i].first);else break;
}
return result;
整体C++代码如下:
class Solution {
private:void searchBST(TreeNode* cur, unordered_map<int, int>& map) { // 前序遍历if (cur == NULL) return ;map[cur->val]++; // 统计元素频率searchBST(cur->left, map);searchBST(cur->right, map);return ;
}
bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {return a.second > b.second;
}
public:vector<int> findMode(TreeNode* root) {unordered_map<int, int> map; // key:元素,value:出现频率vector<int> result;if (root == NULL) return result;searchBST(root, map);vector<pair<int, int>> vec(map.begin(), map.end());sort(vec.begin(), vec.end(), cmp); // 给频率排个序result.push_back(vec[0].first);for (int i = 1; i < vec.size(); i++) {// 取最高的放到result数组中if (vec[i].second == vec[0].second) result.push_back(vec[i].first);else break;}return result;}
};
所以如果本题没有说是二叉搜索树的话,那么就按照上面的思路写!
二叉搜索树
既然是搜索树,它中序遍历就是有序的。
如图:

中序遍历代码如下:
void searchBST(TreeNode* cur) {if (cur == NULL) return ;searchBST(cur->left); // 左(处理节点) // 中searchBST(cur->right); // 右return ;
}
遍历有序数组的元素出现频率,从头遍历,那么一定是相邻两个元素作比较,然后就把出现频率最高的元素输出就可以了。
关键是在有序数组上的话,好搞,在树上怎么搞呢?
这就考察对树的操作了。
在上一篇博客中我们就使用了pre指针和cur指针的技巧,这次又用上了。
弄一个指针指向前一个节点,这样每次cur(当前节点)才能和pre(前一个节点)作比较。
而且初始化的时候pre = NULL,这样当pre为NULL时候,我们就知道这是比较的第一个元素。
代码如下:
if (pre == NULL) { // 第一个节点count = 1; // 频率为1
} else if (pre->val == cur->val) { // 与前一个节点数值相同count++;
} else { // 与前一个节点数值不同count = 1;
}
pre = cur; // 更新上一个节点
此时又有问题了,因为要求最大频率的元素集合(注意是集合,不是一个元素,可以有多个众数),如果是数组上大家一般怎么办?
应该是先遍历一遍数组,找出最大频率(maxCount),然后再重新遍历一遍数组把出现频率为maxCount的元素放进集合。(因为众数有多个)
这种方式遍历了两遍数组。
那么我们遍历两遍二叉搜索树,把众数集合算出来也是可以的。
但这里其实只需要遍历一次就可以找到所有的众数。
那么如何只遍历一遍呢?
如果 频率count 等于 maxCount(最大频率),当然要把这个元素加入到结果集中(以下代码为result数组),代码如下:
if (count == maxCount) { // 如果和最大值相同,放进result中result.push_back(cur->val);
}
是不是感觉这里有问题,result怎么能轻易就把元素放进去了呢,万一,这个maxCount此时还不是真正最大频率呢。
所以下面要做如下操作:
频率count 大于 maxCount的时候,不仅要更新maxCount,而且要清空结果集(以下代码为result数组),因为结果集之前的元素都失效了。
if (count > maxCount) { // 如果计数大于最大值maxCount = count; // 更新最大频率result.clear(); // 很关键的一步,不要忘记清空result,之前result里的元素都失效了result.push_back(cur->val);
}
关键代码都讲完了,完整代码如下:(只需要遍历一遍二叉搜索树,就求出了众数的集合)
class Solution {
private:int maxCount = 0; // 最大频率int count = 0; // 统计频率TreeNode* pre = NULL;vector<int> result;void searchBST(TreeNode* cur) {if (cur == NULL) return ;searchBST(cur->left); // 左// 中if (pre == NULL) { // 第一个节点count = 1;} else if (pre->val == cur->val) { // 与前一个节点数值相同count++;} else { // 与前一个节点数值不同count = 1;}pre = cur; // 更新上一个节点if (count == maxCount) { // 如果和最大值相同,放进result中result.push_back(cur->val);}if (count > maxCount) { // 如果计数大于最大值频率maxCount = count; // 更新最大频率result.clear(); // 很关键的一步,不要忘记清空result,之前result里的元素都失效了result.push_back(cur->val);}searchBST(cur->right); // 右return ;}public:vector<int> findMode(TreeNode* root) {count = 0;maxCount = 0;pre = NULL; // 记录前一个节点result.clear();searchBST(root);return result;}
};
迭代法
只要把中序遍历转成迭代,中间节点的处理逻辑完全一样。
下面我给出其中的一种中序遍历的迭代法,其中间处理逻辑一点都没有变(我从递归法直接粘过来的代码,连注释都没改)
代码如下:
class Solution {
public:vector<int> findMode(TreeNode* root) {stack<TreeNode*> st;TreeNode* cur = root;TreeNode* pre = NULL;int maxCount = 0; // 最大频率int count = 0; // 统计频率vector<int> result;while (cur != NULL || !st.empty()) {if (cur != NULL) { // 指针来访问节点,访问到最底层st.push(cur); // 将访问的节点放进栈cur = cur->left; // 左} else {cur = st.top();st.pop(); // 中if (pre == NULL) { // 第一个节点count = 1;} else if (pre->val == cur->val) { // 与前一个节点数值相同count++;} else { // 与前一个节点数值不同count = 1;}if (count == maxCount) { // 如果和最大值相同,放进result中result.push_back(cur->val);}if (count > maxCount) { // 如果计数大于最大值频率maxCount = count; // 更新最大频率result.clear(); // 很关键的一步,不要忘记清空result,之前result里的元素都失效了result.push_back(cur->val);}pre = cur;cur = cur->right; // 右}}return result;}
};
总结
本题在递归法中,给出了如果是普通二叉树,应该怎么求众数。
知道了普通二叉树的做法时候,再进一步给出二叉搜索树又应该怎么求众数,这样鲜明的对比,相信会对二叉树又有更深层次的理解了。
在递归遍历二叉搜索树的过程中还介绍了一个统计最高出现频率元素集合的技巧, 要不然就要遍历两次二叉搜索树才能把这个最高出现频率元素的集合求出来。
为什么没有这个技巧一定要遍历两次呢? 因为要求的是集合,会有多个众数,如果规定只有一个众数,那么就遍历一次稳稳的了。
最后给出对应的迭代法,其实就是迭代法中序遍历的模板加上递归法中中间节点的处理逻辑。
相关文章:

代码随想录阅读笔记-二叉树【二叉搜索树中的众数】
题目 给定一个有相同值的二叉搜索树(BST),找出 BST 中的所有众数(出现频率最高的元素)。 假定 BST 有如下定义: 结点左子树中所含结点的值小于等于当前结点的值结点右子树中所含结点的值大于等于当前结点的…...

AcWing-游戏
1388. 游戏 - AcWing题库 所需知识:博弈论,区间dp 由于双方都采取最优的策略来取数字,所以结果为确定的,有可能会有多个不同的过程,但是我们只需要关注最终结果就行了。 方法一: 定义dp[i][j] 表示区间…...

Mybatis——一对一映射
一对一映射 预置条件 在某网络购物系统中,一个用户只能拥有一个购物车,用户与购物车的关系可以设计为一对一关系 数据库表结构(唯一外键关联) 创建两个实体类和映射接口 package org.example.demo;import lombok.Data;import …...

Web 安全之 SSL 剥离攻击详解
目录 SSL/TLS简介 SSL 剥离攻击原理 SSL 剥离攻击的影响 SSL 剥离攻击的防范措施 小结 SSL 剥离攻击(SSL Stripping Attack)是一种针对安全套接层(SSL)或传输层安全性(TLS)协议的攻击手段,…...
)
数据结构——顺序表(C语言)
目录 一、顺序表概念 二、顺序表分类 1.静态顺序表 2.动态顺序表 三、顺序表的实现 1.顺序表的结构体定义 2. 顺序表初始化 3.顺序表销毁 4.顺序表的检验 5.顺序表打印 6.顺序表扩容 7.顺序表尾插与头插 8.尾删与头删 9.在pos处插入数据 10.在pos处删除数据 11.查找数据 …...
利用Idea实现Ajax登录(maven工程)
一、新建一个maven工程(不会建的小伙伴可以参考Idea引入maven工程依赖(保姆级)-CSDN博客),工程目录如图 js文件可以上up网盘提取 链接:https://pan.baidu.com/s/1yOFtiZBWGJY64fa2tM9CYg?pwd5555 提取码&…...

环信IM集成教程——Web端UIKit快速集成与消息发送
写在前面: 千呼万唤始出来,环信Web端终于出UIKit了!🎉🎉🎉 文档地址:https://doc.easemob.com/uikit/chatuikit/web/chatuikit_overview.html 环信单群聊 UIKit 是基于环信即时通讯云 IM SDK 开…...

Anaconda如何切换国内镜像源
一、anaconda如何切换阿里镜像源 在Anaconda中切换到阿里云镜像源可以通过以下步骤进行: 1、打开终端(Windows)或者命令行界面(macOS/Linux)。 2、执行以下命令来配置阿里云镜像源: conda config --add…...

Android 14.0 添加自定义服务,并生成jar给第三方app调用
1.概述 在14.0系统ROM产品定制化开发中,由于需要新增加自定义的功能,所以要增加自定义服务,而app上层通过调用自定义服务,来调用相应的功能,所以系统需要先生成jar,然后生成jar 给上层app调用,接下来就来分析实现的步骤,然后来实现相关的功能 从而来实现所需要的功能 …...

解决沁恒ch592单片机在tmos中使用USB总线时,接入USB Hub无法枚举频繁Reset的问题
开发产品时采用了沁恒ch592,做USB开发时遇到了一个奇葩的无法枚举问题。 典型症状 使用USB线直连电脑时没有问题,可以正常使用。 如果接入某些特定方案的USB Hub(例如GL3510、GL3520),可能会出现以下2种情况…...
nvm保姆级安装使用教程
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: 开发环境篇 ✨特色专栏: M…...

大语言模型LLM《提示词工程指南》学习笔记02
文章目录 大语言模型LLM《提示词工程指南》学习笔记02设计提示时需要记住的一些技巧零样本提示少样本提示链式思考(CoT)提示自我一致性生成知识提示 大语言模型LLM《提示词工程指南》学习笔记02 设计提示时需要记住的一些技巧 指令 您可以使用命令来指…...
【realme x2手机解锁BootLoader(简称BL)】
realme手机解锁常识 https://www.realme.com/cn/support/kw/doc/2031665 realme手机解锁支持型号 https://www.realmebbs.com/post-details/1275426081138028544 realme x2手机解锁实践 参考:https://www.realmebbs.com/post-details/1255473809142591488 1 下载apk…...

攻防世界 wife_wife
在这个 JavaScript 示例中,有两个对象:baseUser 和 user。 baseUser 对象定义如下: baseUser { a: 1 } 这个对象有一个属性 a,其值为 1,没有显式指定原型对象,因此它将默认继承 Object.prototype。 …...
Visual Studio安装下载进度为零已解决
因为在安装pytorch3d0.3.0时遇到问题,提示没有cl.exe,VS的C编译组件,可以添加组件也可以重装VS。查了下2019版比2022问题少,选择了安装2019版,下面是下载安装时遇到的问题记录,关于下载进度为零网上有三类解…...

矩阵空间秩1矩阵小世界图
文章目录 1. 矩阵空间2. 微分方程3. 秩为1的矩阵4. 图 1. 矩阵空间 我们以3X3的矩阵空间 M 为例来说明相关情况。目前矩阵空间M中只关心两类计算,矩阵加法和矩阵数乘。 对称矩阵-子空间-有6个3X3的对称矩阵,所以为6维矩阵空间上三角矩阵-子空间-有6个3…...
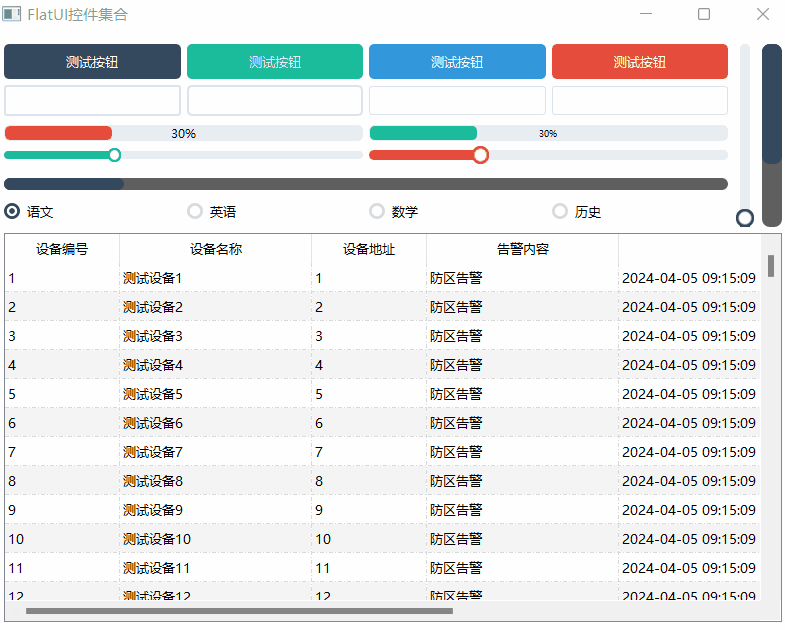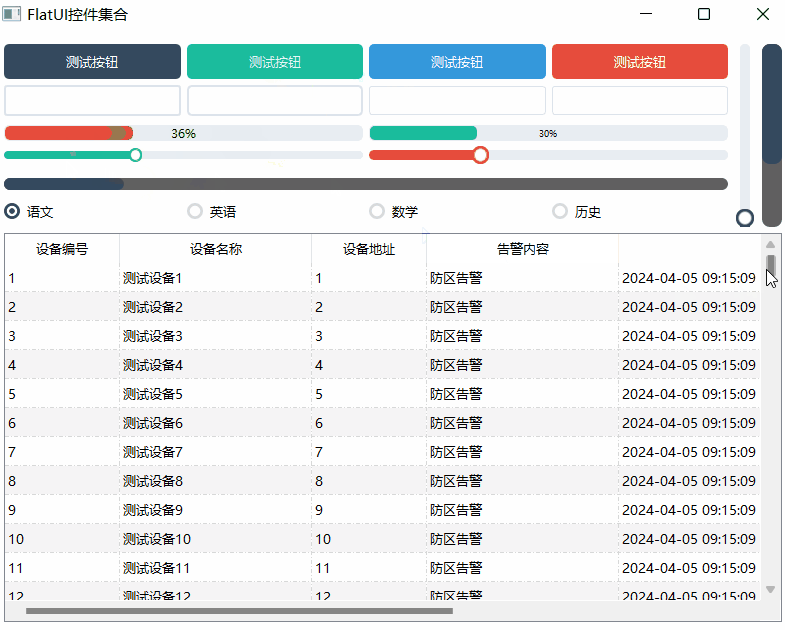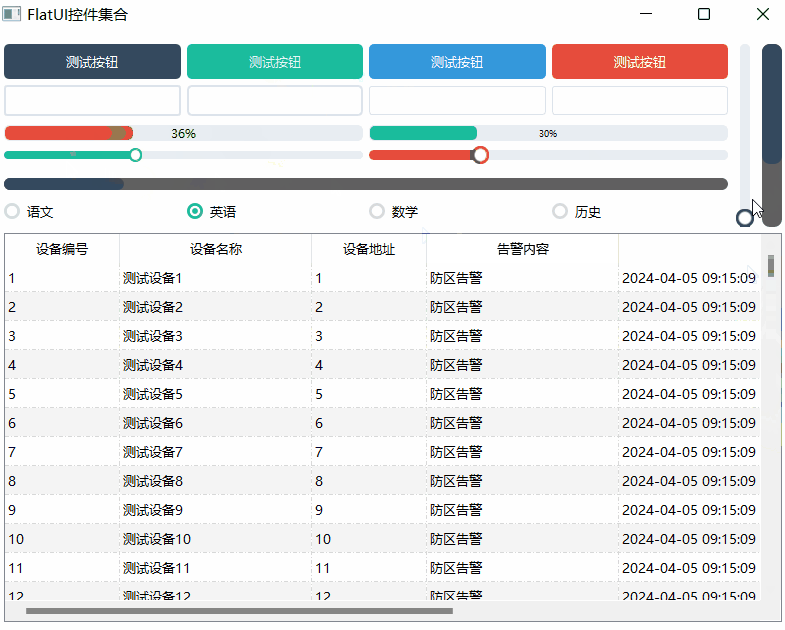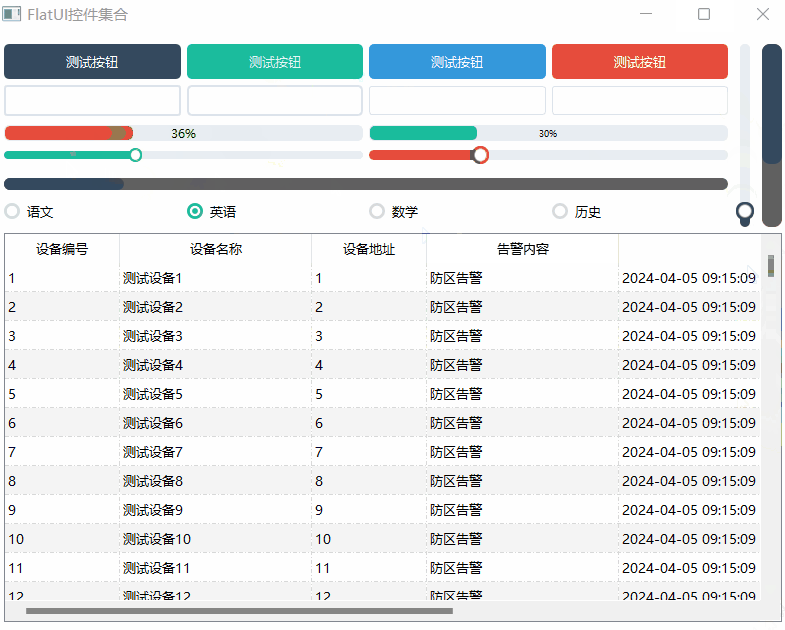
《QT实用小工具·十三》FlatUI辅助类之各种炫酷的控件集合
1、概述 源码放在文章末尾 FlatUI辅助类之各种炫酷的控件集合 按钮样式设置。文本框样式设置。进度条样式。滑块条样式。单选框样式。滚动条样式。可自由设置对象的高度宽度大小等。自带默认参数值。 下面是demo演示: 项目部分代码如下所示: #ifnd…...
dm8 备份与恢复
dm8 备份与恢复 基础环境 操作系统:Red Hat Enterprise Linux Server release 7.9 (Maipo) 数据库版本:DM Database Server 64 V8 架构:单实例1 设置bak_path路径 --创建备份文件存放目录 su - dmdba mkdir -p /dm8/backup--修改dm.ini 文件…...
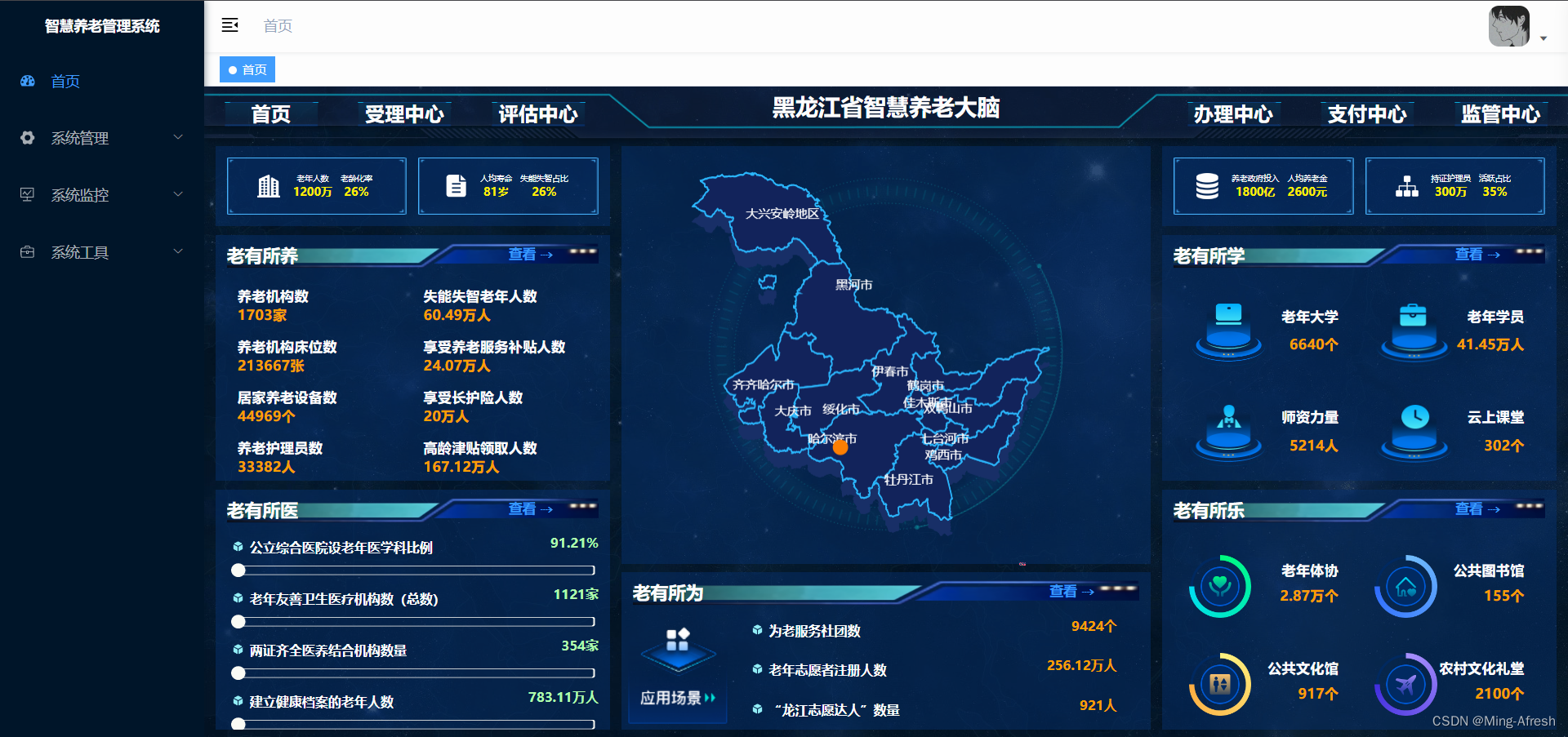
Vue项目中引入html页面(vue.js中引入echarts数据大屏html [静态非数据传递!] )
在项目原有vue(例如首页)基础上引入html页面 1、存放位置 vue3原有public文件夹下 我这边是新建一个static文件夹 专门存放要用到的html文件 复制拖拽过来 index为html的首页 2、更改路径引入到vue中 这里用到的是 iframe 方法 不同于vue的 component…...

ASTM C1186-22 纤维水泥平板
以无石棉类无机矿物纤维、有机合成纤维或纤维素纤维,单独或混合作为增强材料,以普通硅酸盐水泥或水泥中添加硅质、钙质材料代替部分水泥为胶凝材料,经制浆、成型、蒸汽或高压蒸汽养护制成的板材,俗称水泥压力板。 ASTM C1186-22纤…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
