大语言模型LLM《提示词工程指南》学习笔记02
文章目录
- 大语言模型LLM《提示词工程指南》学习笔记02
- 设计提示时需要记住的一些技巧
- 零样本提示
- 少样本提示
- 链式思考(CoT)提示
- 自我一致性
- 生成知识提示
大语言模型LLM《提示词工程指南》学习笔记02
设计提示时需要记住的一些技巧
指令
您可以使用命令来指示模型执行各种简单任务,例如“写入”、“分类”、“总结”、“翻译”、“排序”等,从而为各种简单任务设计有效的提示。
具体性
对您希望模型执行的指令和任务非常具体。提示越具体和详细,结果就越好。当您有所期望的结果或生成样式时,这一点尤为重要。没有特定的令牌或关键字会导致更好的结果。更重要的是具有良好的格式和描述性提示。实际上,在提示中提供示例非常有效,可以以特定格式获得所需的输出。
做还是不做?
设计提示时的另一个常见技巧是避免说不要做什么,而是说要做什么。这鼓励更具体化,并关注导致模型产生良好响应的细节。
零样本提示
提示:
将文本分类为中性、负面或正面。
文本:我认为这次假期还可以。
情感:
输出:
中性
少样本提示
提示:
“whatpu”是坦桑尼亚的一种小型毛茸茸的动物。一个使用whatpu这个词的句子的例子是:
我们在非洲旅行时看到了这些非常可爱的whatpus。
“farduddle”是指快速跳上跳下。一个使用farduddle这个词的句子的例子是:
输出:
当我们赢得比赛时,我们都开始庆祝跳跃。
链式思考(CoT)提示
提示:
这组数中的奇数加起来是偶数:4、8、9、15、12、2、1。
A:将所有奇数相加(9、15、1)得到25。答案为False。这组数中的奇数加起来是偶数:17、10、19、4、8、12、24。
A:将所有奇数相加(17、19)得到36。答案为True。这组数中的奇数加起来是偶数:16、11、14、4、8、13、24。
A:将所有奇数相加(11、13)得到24。答案为True。这组数中的奇数加起来是偶数:17、9、10、12、13、4、2。
A:将所有奇数相加(17、9、13)得到39。答案为False。这组数中的奇数加起来是偶数:15、32、5、13、82、7、1。
A:
输出:
将所有奇数相加(15、5、13、7、1)得到41。答案为False。
提示:
我去市场买了10个苹果。我给了邻居2个苹果和修理工2个苹果。然后我去买了5个苹果并吃了1个。我还剩下多少苹果?
输出:
11个苹果
答案是不正确的!现在让我们尝试使用特殊提示。
提示:
我去市场买了10个苹果。我给了邻居2个苹果和修理工2个苹果。然后我去买了5个苹果并吃了1个。我还剩下多少苹果?
让我们逐步思考。
输出:
首先,您从10个苹果开始。
您给了邻居和修理工各2个苹果,所以您还剩下6个苹果。
然后您买了5个苹果,所以现在您有11个苹果。
最后,您吃了1个苹果,所以您还剩下10个苹果。
自我一致性
提示:
Q:林中有15棵树。林业工人今天将在林中种树。完成后,将有21棵树。林业工人今天种了多少棵树?
A:我们从15棵树开始。后来我们有21棵树。差异必须是他们种树的数量。因此,他们必须种了21-15 = 6棵树。答案是6。
Q:停车场有3辆汽车,又来了2辆汽车,停车场有多少辆汽车?
A:停车场已经有3辆汽车。又来了2辆。现在有3 + 2 = 5辆汽车。答案是5。
Q:Leah有32块巧克力,她的姐姐有42块。如果他们吃了35块,他们总共还剩多少块?
A:Leah有32块巧克力,Leah的姐姐有42块。这意味着最初有32 + 42 = 74块巧克力。已经吃了35块。因此,他们总共还剩74-35 = 39块巧克力。答案是39。
Q:Jason有20个棒棒糖。他给Denny一些棒棒糖。现在Jason只有12个棒棒糖。Jason给Denny多少棒棒糖?
A:Jason有20个棒棒糖。因为他现在只有12个,所以他必须把剩下的给Denny。他给Denny的棒棒糖数量必须是20-12 = 8个棒棒糖。答案是8。
Q:Shawn有五个玩具。圣诞节,他从他的父母那里得到了两个玩具。他现在有多少个玩具?
A:他有5个玩具。他从妈妈那里得到了2个,所以在那之后他有5 + 2 = 7个玩具。然后他从爸爸那里得到了2个,所以总共他有7 + 2 = 9个玩具。答案是9。
Q:服务器房间里有9台计算机。从周一到周四,每天都会安装5台计算机。现在服务器房间里有多少台计算机?
A:从周一到周四有4天。每天都添加了5台计算机。这意味着总共添加了4 * 5 =
20台计算机。一开始有9台计算机,所以现在有9 + 20 = 29台计算机。答案是29。
Q:Michael有58个高尔夫球。星期二,他丢失了23个高尔夫球。星期三,他又丢失了2个。星期三结束时他还剩多少个高尔夫球?
A:Michael最初有58个球。星期二他丢失了23个,所以在那之后他有58-23 = 35个球。星期三他又丢失了2个,所以现在他有35-2 = 33个球。答案是33。
Q:Olivia有23美元。她用每个3美元的价格买了五个百吉饼。她还剩多少钱?
A:她用每个3美元的价格买了5个百吉饼。这意味着她花了15美元。她还剩8美元。
Q:当我6岁时,我的妹妹是我的一半年龄。现在我70岁了,我的妹妹多大?
A:
输出 1:
当我6岁时,我的妹妹是我的一半年龄,也就是3岁。现在我70岁了,所以她是70-3 = 67岁。答案是67。
输出 2:
当叙述者6岁时,他的妹妹是他年龄的一半,也就是3岁。现在叙述者70岁了,他的妹妹应该是70-3 = 67岁。答案是67。
输出 3:
当我6岁时,我的妹妹是我的一半年龄,也就是3岁。现在我70岁了,所以她是70/2 = 35岁。答案是35。
生成知识提示
提示:
输入:希腊比墨西哥大。
知识:希腊的面积约为131,957平方公里,而墨西哥的面积约为1,964,375平方公里,使墨西哥比希腊大了1,389%。
输入:眼镜总是会起雾。
知识:当你的汗水、呼吸和周围的湿度中的水蒸气落在冷的表面上,冷却并变成微小的液滴时,会在眼镜镜片上产生冷凝。你看到的是一层薄膜。你的镜片相对于你的呼吸会比较凉,尤其是当外面的空气很冷时。
输入:鱼有思考能力。
知识:鱼比它们看起来更聪明。在许多领域,如记忆力,它们的认知能力与或超过非人类灵长类动物等“更高级”的脊椎动物。鱼的长期记忆帮助它们跟踪复杂的社交关系。
输入:一个人一生中吸烟很多香烟的常见影响是患肺癌的几率高于正常水平。
知识:那些一生中平均每天吸烟不到一支香烟的人,患肺癌的风险是从不吸烟者的9倍。在每天吸烟1到10支香烟之间的人群中,死于肺癌的风险几乎是从不吸烟者的12倍。
输入:一块石头和一颗卵石大小相同。
知识:卵石是一种根据Udden-Wentworth沉积学尺度的颗粒大小为4到64毫米的岩屑。卵石通常被认为比颗粒(直径2到4毫米)大,比卵石(直径64到256毫米)小。
输入:高尔夫球的一部分是试图获得比其他人更高的得分。
知识:
知识1:
高尔夫球的目标是以最少的杆数打完一组洞。一轮高尔夫球比赛通常包括18个洞。每个洞在标准高尔夫球场上一轮只打一次。每个杆计为一分,总杆数用于确定比赛的获胜者。
知识2:
高尔夫球是一项精密的球杆运动,竞争选手(或高尔夫球手)使用许多类型的球杆,用最少的杆数将球打入球场上一系列洞中。目标是以最低的分数完成比赛,该分数是通过将每个洞上所用的杆数相加计算出来的。得分最低的选手赢得比赛。
我们使用 Liu等人2022 的论文中提供的提示。
下一步是将知识整合并得出预测。我将问题重新格式化为 QA 格式,以指导答案格式。
提示:
问题:高尔夫球的一部分是试图获得比其他人更高的得分。是或否?
知识:高尔夫球的目标是以最少的杆数打完一组洞。一轮高尔夫球比赛通常包括18个洞。每个洞在标准高尔夫球场上一轮只打一次。每个杆计为一分,总杆数用于确定比赛的获胜者。
解释和答案:
答案 1(置信度非常高):
不是,高尔夫球的目标不是获得比其他人更高的得分。相反,目标是以最少的杆数打完一组洞。总杆数用于确定比赛的获胜者,而不是总得分。
问题:高尔夫球的一部分是试图获得比其他人更高的得分。是或否?
知识:高尔夫球是一项精密的球杆运动,竞争选手(或高尔夫球手)使用许多类型的球杆,用最少的杆数将球打入球场上一系列洞中。目标是以最低的分数完成比赛,该分数是通过将每个洞上所用的杆数相加计算出来的。得分最低的选手赢得比赛。
解释和答案:
答案 2(置信度要低得多):
是的,高尔夫球的一部分是试图获得比其他人更高的得分。每个选手都试图以最少的杆数打完一组洞。总杆数用于确定比赛的获胜者,而不是总得分。得分最低的选手赢得比赛。
相关文章:

大语言模型LLM《提示词工程指南》学习笔记02
文章目录 大语言模型LLM《提示词工程指南》学习笔记02设计提示时需要记住的一些技巧零样本提示少样本提示链式思考(CoT)提示自我一致性生成知识提示 大语言模型LLM《提示词工程指南》学习笔记02 设计提示时需要记住的一些技巧 指令 您可以使用命令来指…...
【realme x2手机解锁BootLoader(简称BL)】
realme手机解锁常识 https://www.realme.com/cn/support/kw/doc/2031665 realme手机解锁支持型号 https://www.realmebbs.com/post-details/1275426081138028544 realme x2手机解锁实践 参考:https://www.realmebbs.com/post-details/1255473809142591488 1 下载apk…...

攻防世界 wife_wife
在这个 JavaScript 示例中,有两个对象:baseUser 和 user。 baseUser 对象定义如下: baseUser { a: 1 } 这个对象有一个属性 a,其值为 1,没有显式指定原型对象,因此它将默认继承 Object.prototype。 …...
Visual Studio安装下载进度为零已解决
因为在安装pytorch3d0.3.0时遇到问题,提示没有cl.exe,VS的C编译组件,可以添加组件也可以重装VS。查了下2019版比2022问题少,选择了安装2019版,下面是下载安装时遇到的问题记录,关于下载进度为零网上有三类解…...

矩阵空间秩1矩阵小世界图
文章目录 1. 矩阵空间2. 微分方程3. 秩为1的矩阵4. 图 1. 矩阵空间 我们以3X3的矩阵空间 M 为例来说明相关情况。目前矩阵空间M中只关心两类计算,矩阵加法和矩阵数乘。 对称矩阵-子空间-有6个3X3的对称矩阵,所以为6维矩阵空间上三角矩阵-子空间-有6个3…...
《QT实用小工具·十三》FlatUI辅助类之各种炫酷的控件集合
1、概述 源码放在文章末尾 FlatUI辅助类之各种炫酷的控件集合 按钮样式设置。文本框样式设置。进度条样式。滑块条样式。单选框样式。滚动条样式。可自由设置对象的高度宽度大小等。自带默认参数值。 下面是demo演示: 项目部分代码如下所示: #ifnd…...
dm8 备份与恢复
dm8 备份与恢复 基础环境 操作系统:Red Hat Enterprise Linux Server release 7.9 (Maipo) 数据库版本:DM Database Server 64 V8 架构:单实例1 设置bak_path路径 --创建备份文件存放目录 su - dmdba mkdir -p /dm8/backup--修改dm.ini 文件…...
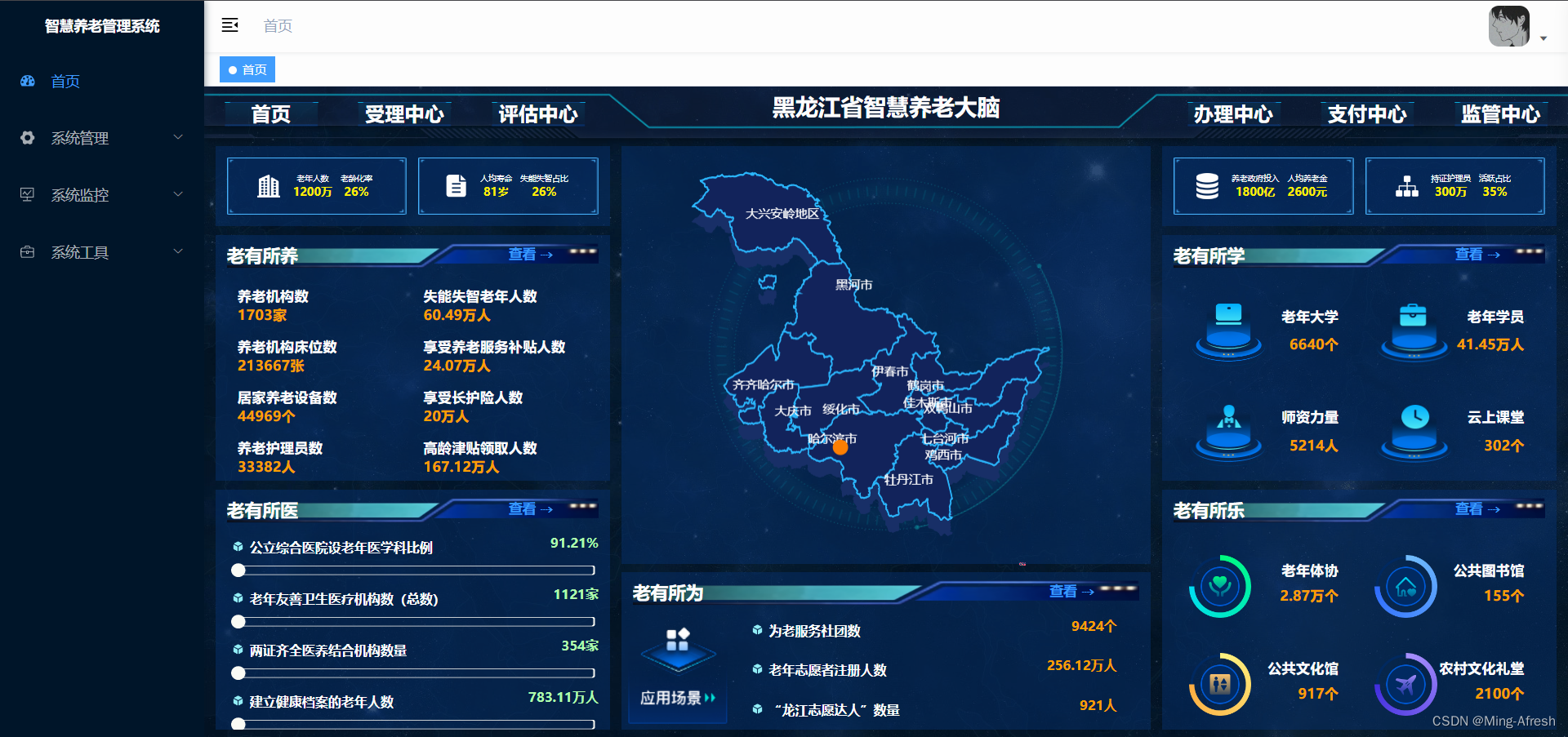
Vue项目中引入html页面(vue.js中引入echarts数据大屏html [静态非数据传递!] )
在项目原有vue(例如首页)基础上引入html页面 1、存放位置 vue3原有public文件夹下 我这边是新建一个static文件夹 专门存放要用到的html文件 复制拖拽过来 index为html的首页 2、更改路径引入到vue中 这里用到的是 iframe 方法 不同于vue的 component…...

ASTM C1186-22 纤维水泥平板
以无石棉类无机矿物纤维、有机合成纤维或纤维素纤维,单独或混合作为增强材料,以普通硅酸盐水泥或水泥中添加硅质、钙质材料代替部分水泥为胶凝材料,经制浆、成型、蒸汽或高压蒸汽养护制成的板材,俗称水泥压力板。 ASTM C1186-22纤…...

NoSQL概述
NoSQL概述 目录 一、为什么用NoSQL 二、什么是NoSQL 三、经典应用分析 四、N o S Q L 数 据 模 型 简 介 五、NoSQL四大分类 六、CAP BASE 一、为什么用NoSQL 1、单机MySQL的美好年代 在90年代,一个网站的访问量一般不大,用单个数据库完全可以轻松应…...
爬虫实战一、Scrapy开发环境(Win10+Anaconda3)搭建
#前言 在这儿推荐使用Anaconda进行安装,并不推荐大家用pythonpip安装,因为pythonpip的坑实在是太多了。 #一、环境中准备: Win10(企业版)Anaconda3-5.0.1-Windows-x86_64,下载地址,如果打不开…...
llama.cpp运行qwen0.5B
编译llama.cp 参考 下载模型 05b模型下载 转化模型 创建虚拟环境 conda create --prefixD:\miniconda3\envs\llamacpp python3.10 conda activate D:\miniconda3\envs\llamacpp安装所需要的包 cd G:\Cpp\llama.cpp-master pip install -r requirements.txt python conver…...
 |GET和POST两种基本请求方法有什么区别)
【接口】HTTP(3) |GET和POST两种基本请求方法有什么区别
在我面试时,在我招人面试别人时,10次能遇到7次这个问题,我听过我也说回答过: Get: 一般对于从服务器取数据的请求可以设置为get方式 Get方式在传递参数的时候,一般都会把参数直接拼接在url上 Get请求方法…...

金陵科技学院软件工程学院软件工程专业
感兴趣的小伙伴可以私信我哦~~ 是笔者写的各种高质量作业和实验哦~~ 感兴趣的小伙伴可以私信我哦~~ 是笔者写的各种高质量作业和实验哦~~ 感兴趣的小伙伴可以私信我哦~~ 是笔者写的各种高质量作业和实验哦~~ 感兴趣的小伙伴可以私信我哦~~ 是笔者写的各种高质量作业和实验哦…...

Android 关于apk反编译d2j-dex2jar classes.dex失败的几种方法
目录 确认路径正确直接定位到指定目录确定目录正确,按如下路径修改下面是未找到相关文件正确操作 确认路径正确 ,即d2j-dex2jar和classes.dex是否都在一个文件夹里(大部分的情况都是路径不正确) 直接定位到指定目录 路径正确的…...

Django--admin 后台管理站点
Django最大的优点之一,就是体贴的提供了一个基于项目model创建的一个后台管理站点admin。这个界面只给站点管理员使用,并不对大众开放。虽然admin的界面可能不是那么美观,功能不是那么强大,内容不一定符合你的要求,但是…...

JavaScript(六)---【回调、异步、promise、Async】
零.前言 JavaScript(一)---【js的两种导入方式、全局作用域、函数作用域、块作用域】-CSDN博客 JavaScript(二)---【js数组、js对象、this指针】-CSDN博客 JavaScript(三)---【this指针,函数定义、Call、Apply、函数绑定、闭包】-CSDN博客 JavaScript(四)---【执…...
vue2+elementUi的两个el-date-picker日期组件进行联动
vue2elementUi的两个el-date-picker日期组件进行联动 <template><el-form><el-form-item label"起始日期"><el-date-picker v-model"form.startTime" change"startTimeChange" :picker-options"startTimePickerOption…...

GIN实例讲解
第一个gin程序 package mainimport ("github.com/gin-gonic/gin" )func main() {// 创建一个 Gin 引擎实例r : gin.Default()// 定义一个 GET 请求的路由,当访问 /hello 路径时执行匿名函数r.GET("/hello", func(c *gin.Context) {// 获取查询…...

开源充电桩设备监控系统技术解决方案
开源 | 慧哥充电桩平台V2.5.2(支持 汽车 电动自行车 云快充1.5、云快充1.6 微服务 ) SpringBoot设备监控系统解决方案 一、引言 1.项目背景 随着物联网技术的快速发展,设备的智能化和网络化程度日益提高。在现代工业和信息化的背景下&#x…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
