java算法day45 | 动态规划part07 ● 70. 爬楼梯 (进阶) ● 322. 零钱兑换 ● 279.完全平方数
70. 爬楼梯 (进阶)
题目描述:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
输入描述:输入共一行,包含两个正整数,分别表示n, m
输出描述:输出一个整数,表示爬到楼顶的方法数。
输入示例:3 2
输出示例:3
提示:
当 m = 2,n = 3 时,n = 3 这表示一共有三个台阶,m = 2 代表你每次可以爬一个台阶或者两个台阶。
此时你有三种方法可以爬到楼顶。
1 阶 + 1 阶 + 1 阶段
1 阶 + 2 阶
2 阶 + 1 阶
-
确定dp数组以及下标的含义
dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法。 -
确定递推公式
在动态规划:494.目标和 (opens new window)、 动态规划:518.零钱兑换II (opens new window)、动态规划:377. 组合总和 Ⅳ (opens new window)中我们都讲过了,求装满背包有几种方法,递推公式一般都是dp[i] += dp[i - nums[j]];
本题呢,dp[i]有几种来源,dp[i - 1],dp[i - 2],dp[i - 3] 等等,即:dp[i - j]
那么递推公式为:dp[i] += dp[i - j] -
dp数组如何初始化
既然递归公式是 dp[i] += dp[i - j],那么dp[0] 一定为1,dp[0]是递归中一切数值的基础所在,如果dp[0]是0的话,其他数值都是0了。
下标非0的dp[i]初始化为0,因为dp[i]是靠dp[i-j]累计上来的,dp[i]本身为0这样才不会影响结果 -
确定遍历顺序
这是背包里求排列问题,即:1、2 步 和 2、1 步都是上三个台阶,但是这两种方法不一样!
所以需将target放在外循环,将nums放在内循环。
每一步可以走多次,这是完全背包,内循环需要从前向后遍历。 -
举例来推导dp数组
import java.util.Scanner;public class Main{public static void main(String[] args){Scanner in=new Scanner(System.in);int n=in.nextInt();int m=in.nextInt();int[] dp=new int[n+1];dp[0]=1;for(int j=1;j<=n;j++){for(int i=0;i<=m;i++){if(j>=i){dp[j]=dp[j]+dp[j-i];}}}System.out.println(dp[n]);}
}时间复杂度:O(mn)
空间复杂度:O(n)
322. 零钱兑换


动规五部曲分析如下:
-
确定dp数组以及下标的含义
dp[j]:凑足总额为j所需钱币的最少个数为dp[j] -
确定递推公式
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); -
dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
其他下标对应的数值呢?
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。 -
确定遍历顺序
本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。
所以本题并不强调集合是组合还是排列。
综上所述,遍历顺序为:coins(物品)放在外循环,target(背包)在内循环。且内循环正序。 -
举例推导dp数组
class Solution {public int coinChange(int[] coins, int amount) {int max=Integer.MAX_VALUE;int[] dp=new int[amount+1];for(int i=0;i<dp.length;i++){dp[i]=max;}dp[0]=0;for(int i=0;i<coins.length;i++){for(int j=coins[i];j<=amount;j++){if(dp[j-coins[i]]!=max){//只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要dp[j]=Math.min(dp[j],dp[j-coins[i]]+1);}}}return dp[amount]==max?-1:dp[amount];}
}
时间复杂度: O(n * amount),其中 n 为 coins 的长度
空间复杂度: O(amount)
279.完全平方数


动规五部曲分析如下:
-
确定dp数组(dp table)以及下标的含义
dp[j]:和为j的完全平方数的最少数量为dp[j] -
确定递推公式
dp[j] 可以由dp[j - i * i]推出, dp[j - i * i] + 1 便可以凑成dp[j]。
此时我们要选择最小的dp[j],所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]); -
dp数组如何初始化
dp[0]表示 和为0的完全平方数的最小数量,那么dp[0]一定是0。
有同学问题,那0 * 0 也算是一种啊,为啥dp[0] 就是 0呢?
看题目描述,找到若干个完全平方数(比如 1, 4, 9, 16, …),题目描述中可没说要从0开始,dp[0]=0完全是为了递推公式。
非0下标的dp[j]应该是多少呢?
从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。 -
确定遍历顺序
我们知道这是完全背包,
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
class Solution {public int numSquares(int n) {int max = Integer.MAX_VALUE;int[] dp = new int[n + 1];for (int j = 0; j <= n; j++) {//初始化dp[j] = max;}dp[0]=0;for(int i=1;i*i<=n;i++){int weight=i*i;for(int j=weight;j<=n;j++){dp[j]=Math.min(dp[j],dp[j-weight]+1);}}return dp[n];}
}
时间复杂度: O(n * √n)
空间复杂度: O(n)
相关文章:

java算法day45 | 动态规划part07 ● 70. 爬楼梯 (进阶) ● 322. 零钱兑换 ● 279.完全平方数
70. 爬楼梯 (进阶) 题目描述: 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬至多m (1 < m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢? 注意:给定 n 是一个正整数。 输入描述:输入…...
HuggingFace踩坑记录-连不上,根本连不上
学习 transformers 的第一步,往往是几句简单的代码 from transformers import pipelineclassifier pipeline("sentiment-analysis") classifier("We are very happy to show you the 🤗 Transformers library.") ""&quo…...

面试题:Spring Boot Starter的功能与使用场景
Spring Boot Starter 是 Spring Boot 框架为了简化项目的初始化和配置工作而设计的一种模块化依赖管理方式。它主要具有以下几个关键功能和使用场景: 功能: 1. 依赖管理每个 Starter 都是一组相关的依赖项集合,这些依赖项都是为了实现特定功能…...
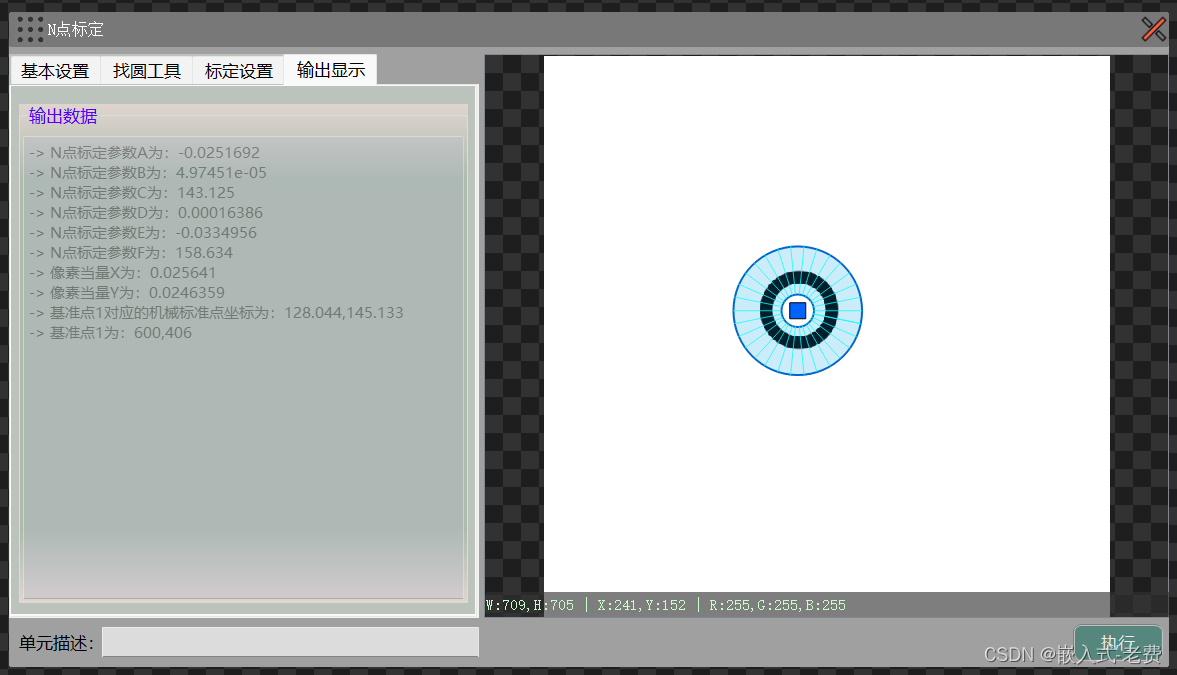
上位机图像处理和嵌入式模块部署(qmacvisual之n点标定)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 工业场景中,很多时候图像是用来做测量的。虽然我们很希望载台是平的,摄像头是正对着拍摄物体的,但是运行时间长…...

Francek Chen 的128天创作纪念日
目录 Francek Chen 的128天创作纪念日机缘收获日常成就憧憬 Francek Chen 的128天创作纪念日 Francek Chen 的个人主页 机缘 不知不觉的加入CSDN已有两年时间了,最初我第一次接触CSDN技术社区是在2022年4月的时候,通过学长给我们推荐了几个IT社区平台&a…...

PyTorch之Torch Script的简单使用
一、参考资料 TorchScript 简介 Torch Script Loading a TorchScript Model in C TorchScript 解读(一):初识 TorchScript libtorch教程(一)开发环境搭建:VSlibtorch和Qtlibtorch 二、Torch Script模型格…...
vscode 连接远程服务器 服务器无法上网 离线配置 .vscode-server
离线配置 vscode 连接远程服务器 .vscode-server 1. .vscode-server下载 使用vscode连接远程服务器时会自动下载配置.vscode-server文件夹,如果远程服务器无法联网,则需要手动下载 1)网址:https://update.code.visualstudio.com…...
arm开发板移植工具mkfs.ext4
文章目录 一、前言二、手动安装e2fsprogs1、下载源码包2、解压源码3、配置4、编译5、安装 三、移植四、验证五、总结 一、前言 在buildroot菜单中,可以通过勾选e2fsprogs工具来安装mkfs.ext4工具: Target packages -> Filesystem and flash utilit…...
某盾滑块拼图验证码增强版
介绍 提示:文章仅供交流学习,严禁用于非法用途,如有不当可联系本人删除 最近某盾新推出了,滑块拼图验证码,如下图所示,这篇文章介绍怎么识别滑块距离相关。 参数attrs 通过GET请求获取的参数attrs, 决…...

这个世界万物存在只有一种关系:博弈
$上证指数(SH000001)$ 我能给各位最大的帮助可能就是第一个从红警游戏引入了情绪周期视角的概念,而这个概念可以帮助很多人理解市场成为一种可能性,如果不理解可以重新回归游戏进行反复体验,你体验的足够多,思考的足够多ÿ…...

c#让不同的工厂生产不同的“鸭肉”
任务目标 实现对周黑鸭工厂的产品生产统一管理,主要产品包括鸭脖和鸭翅。武汉工厂能生生产鸭脖和鸭翅,南京工厂只能生产鸭翅,长沙工厂只能生产鸭脖。 分析任务 我们需要有武汉工厂、南京工厂、长沙工厂的类,类中需要实现生产鸭…...
大数据分析与内存计算——Spark安装以及Hadoop操作——注意事项
一、Spark安装 1.相关链接 Spark安装和编程实践(Spark3.4.0)_厦大数据库实验室博客 (xmu.edu.cn) 2.安装Spark(Local模式) 按照文章中的步骤安装即可 遇到问题:xshell以及xftp不能使用 解决办法: 在…...
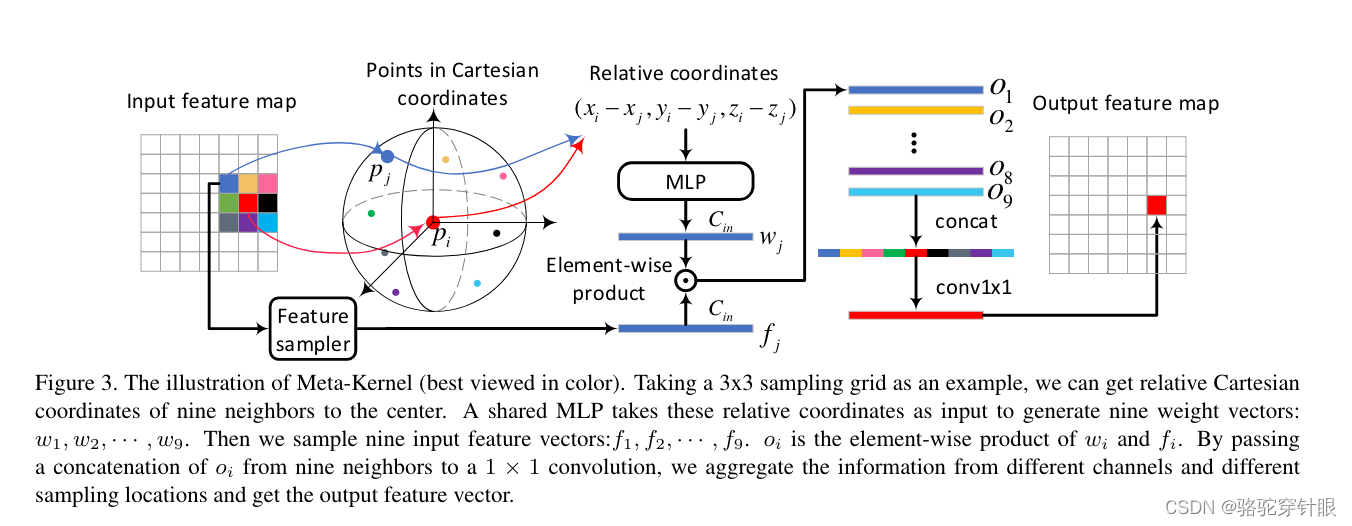
论文阅读RangeDet: In Defense of Range View for LiDAR-based 3D Object Detection
文章目录 RangeDet: In Defense of Range View for LiDAR-based 3D Object Detection问题笛卡尔坐标结构图Meta-Kernel Convolution RangeDet: In Defense of Range View for LiDAR-based 3D Object Detection 论文:https://arxiv.org/pdf/2103.10039.pdf 代码&…...
3D模型格式转换工具HOOPS Exchange如何将3D文件加载到PRC数据结构中?
HOOPS Exchange是一款高效的数据访问工具,专为开发人员设计,用于在不同的CAD(计算机辅助设计)系统之间进行高保真的数据转换和交换。由Tech Soft 3D公司开发,它支持广泛的CAD文件格式,包括但不限于AutoCAD的…...
c# wpf Template ContentTemplate
1.概要 1.1 定义内容的外观 2.2 要点分析 2.代码 <Window x:Class"WpfApp2.Window1"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d"http://schem…...

空和null是两回事
文章目录 前言 StringUtils1. 空(empty):字符串:集合: 2. null:引用类型变量:基本类型变量: 3. isBlank总结: 前言 StringUtils 提示:这里可以添加本文要记录…...

UNIAPP(小程序)每十个文章中间一个广告
三十秒刷新一次广告 ad-intervals"30" <template><view style"margin: 30rpx;"><view class"" v-for"(item,index) in 100"><!-- 广告 --><view style"margin-bottom: 20rpx;" v-if"(inde…...

pip包安装用国内镜像源
一:临时用国内源 可以在使用pip的时候加参数-i https://pypi.tuna.tsinghua.edu.cn/simple 例如:pip install -i https://pypi.tuna.tsinghua.edu.cn/simple pyspider,这样就会从清华这边的镜像去安装pyspider库 清华:https://py…...

uniapp:小程序腾讯地图程序文件qqmap-wx-jssdk.js 文件一直找不到无法导入
先看问题: 在使用腾讯地图api时无法导入到qqmap-wx-jssdk.js文件 解决方法:1、打开qqmap-wx-jssdk.js最后一行 然后导入:这里是我的路径位置,可以根据自己的路径位置进行更改导入 最后在生命周期函数中输出: 运行效果…...
)
如何物理控制另一台电脑以及无网络用作副屏(现成设备和使用)
初级代码游戏的专栏介绍与文章目录-CSDN博客 我的github:codetoys,所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。 这些代码大部分以Linux为目标但部分代码是纯C的,可以在任何平台上使用。 控制另一台电脑有很多方法&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
