35 openEuler搭建repo(yum)服务器-创建、更新本地repo源
文章目录
- 35 openEuler搭建repo(yum)服务器-创建、更新本地repo源
- 35.1 获取ISO发布包
- 35.2 挂载ISO创建repo源
- 35.3 创建本地repo源
- 35.4 更新repo源
35 openEuler搭建repo(yum)服务器-创建、更新本地repo源
使用mount挂载,将openEuler的ISO发布包openEuler-22.03-LTS-everything-x86_64-dvd.iso创建为本地repo源,并能够对repo源进行更新。
35.1 获取ISO发布包
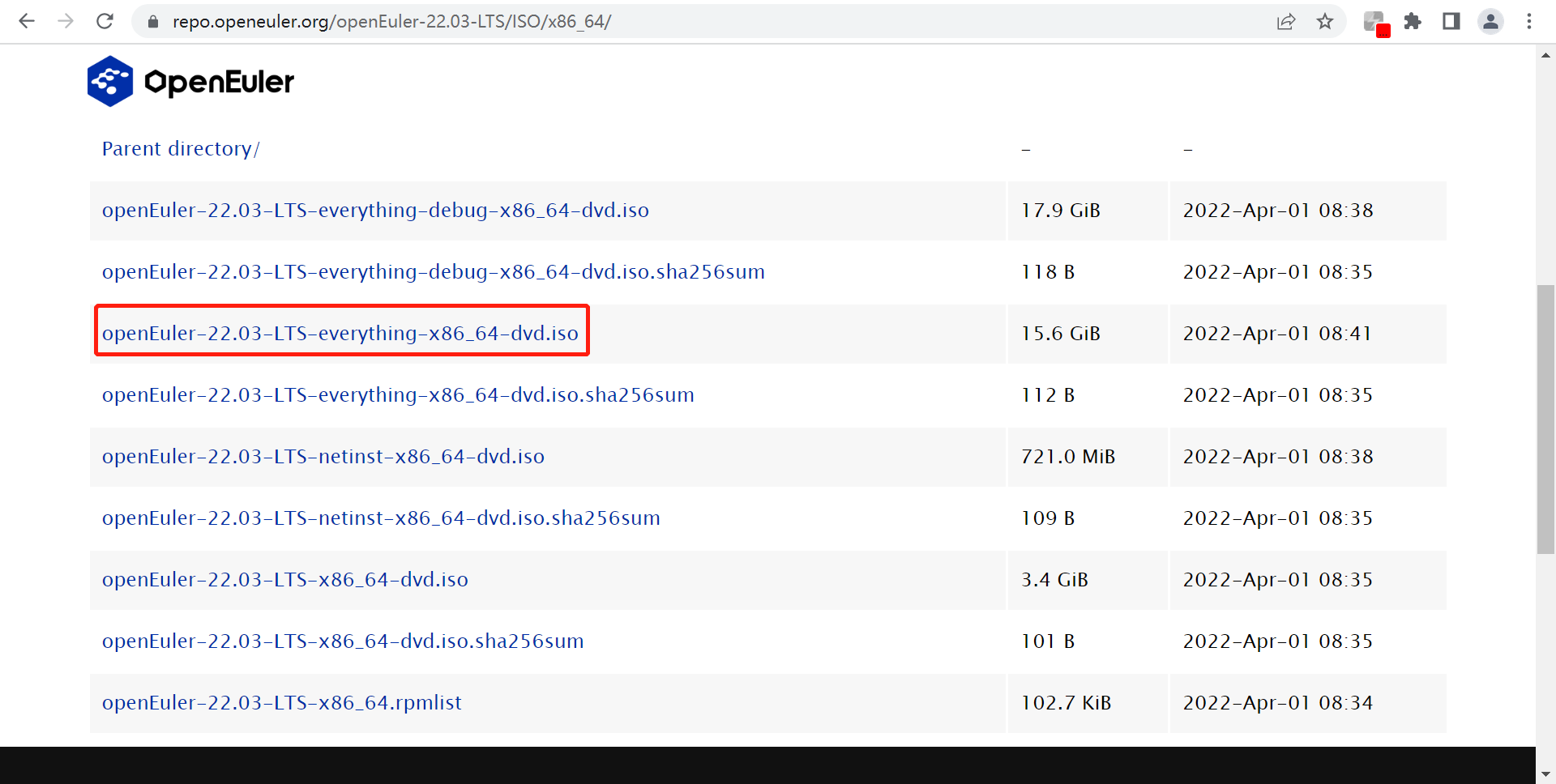
请从如下网址获取openEuler的ISO发布包。
https://repo.openeuler.org/openEuler-22.03-LTS/ISO/
35.2 挂载ISO创建repo源
-
将openEuler-22.03-LTS-everything-x86_64-dvd.iso上传到/home目录。
-
在root权限下使用mount命令挂载ISO发布包。
# mount -o loop /home/openEuler-22.03-LTS-everything-x86_64-dvd.iso /mnt
例如示例命令如下:
[root@repo ~]# mount -o loop /home/openEuler-22.03-LTS-everything-x86_64-dvd.iso /mnt
mount: /mnt: WARNING: source write-protected, mounted read-only.
[root@repo ~]#
[root@repo ~]# df -h
文件系统 容量 已用 可用 已用% 挂载点
devtmpfs 1.7G 0 1.7G 0% /dev
tmpfs 1.7G 12K 1.7G 1% /dev/shm
tmpfs 677M 9.1M 668M 2% /run
tmpfs 4.0M 0 4.0M 0% /sys/fs/cgroup
/dev/mapper/vg00-lv_root 41G 19G 20G 48% /
tmpfs 1.7G 0 1.7G 0% /tmp
/dev/sda1 974M 88M 819M 10% /boot
/dev/loop0 16G 16G 0 100% /mnt
[root@repo ~]#
- 挂载好的mnt目录如下:
# tree -d /mnt
例如示例命令如下:
[root@repo ~]# tree -d /mnt
/mnt
├── docs
├── EFI
│ └── BOOT
│ └── fonts
├── images
│ └── pxeboot
├── isolinux
├── ks
├── Packages
└── repodata10 directories
[root@repo ~]#
其中,Packages为rpm包所在的目录,repodata为repo源元数据所在的目录,RPM-GPG-KEY-openEuler为openEuler的签名公钥。
35.3 创建本地repo源
- 可以拷贝ISO发布包中相关文件至本地目录以创建本地repo源。
# mount -o loop /home/openEuler-22.03-LTS-everything-x86_64-dvd.iso /mnt
# mkdir -p /home/repo
# cp -r /mnt/* /home/repo/
例如示例命令如下:
[root@repo ~]# mount -o loop /home/openEuler-22.03-LTS-everything-x86_64-dvd.iso /mnt
mount: /mnt: WARNING: source write-protected, mounted read-only.
[root@repo ~]#
[root@repo ~]# mkdir -p /home/repo
[root@repo ~]#
[root@repo ~]# cp -r /mnt/* /home/repo/
[root@repo ~]#
- 从而本地repo目录如下:
# tree -d /home/repo
例如示例命令如下:
[root@repo ~]# tree -d /home/repo
/home/repo
├── docs
├── EFI
│ └── BOOT
│ └── fonts
├── images
│ └── pxeboot
├── isolinux
├── ks
├── Packages
└── repodata10 directories
[root@repo ~]#
Packages为rpm包所在的目录,repodata为repo源元数据所在的目录,RPM-GPG-KEY-openEuler为openEuler的签名公钥。
35.4 更新repo源
更新repo源有两种方式:
- 通过新版本的ISO更新已有的repo源,与创建repo源的方式相同,即挂载ISO发布包或重新拷贝ISO发布包至本地目录。
- 在repo源的Packages目录下添加rpm包,然后通过createrepo命令更新repo源。
# createrepo --update --workers=10 /home/repo
其中,–update表示更新,–workers表示线程数,可自定义。
说明:
若命令打印信息为“createrepo:未找到命令”,则表示未安装createrepo软件,可在root权限下执行dnf install createrepo进行安装。
例如示例命令如下:
[root@repo ~]# createrepo --update --workers=10 /home/repo
-bash: createrepo:未找到命令
[root@repo ~]#
[root@repo ~]# dnf install createrepo -y
Last metadata expiration check: 1:11:41 ago on 2022年11月29日 星期二 20时22分38秒.
Dependencies resolved.
=============================================================================================================================Package Architecture Version Repository Size
=============================================================================================================================
Installing:createrepo_c x86_64 0.17.6-1.oe2203 OS 137 k
Installing dependencies:drpm x86_64 0.5.0-2.oe2203 update 60 kTransaction Summary
=============================================================================================================================
Install 2 PackagesTotal download size: 197 k
Installed size: 535 k
Downloading Packages:
(1/2): drpm-0.5.0-2.oe2203.x86_64.rpm 331 kB/s | 60 kB 00:00
(2/2): createrepo_c-0.17.6-1.oe2203.x86_64.rpm 539 kB/s | 137 kB 00:00
-----------------------------------------------------------------------------------------------------------------------------
Total 722 kB/s | 197 kB 00:00
retrieving repo key for OS unencrypted from http://repo.openeuler.org/openEuler-22.03-LTS/OS/x86_64/RPM-GPG-KEY-openEuler
OS 14 kB/s | 2.1 kB 00:00
Importing GPG key 0xB25E7F66:Userid : "private OBS (key without passphrase) <defaultkey@localobs>"Fingerprint: 12EA 74AC 9DF4 8D46 C69C A0BE D557 065E B25E 7F66From : http://repo.openeuler.org/openEuler-22.03-LTS/OS/x86_64/RPM-GPG-KEY-openEuler
Key imported successfully
Running transaction check
Transaction check succeeded.
Running transaction test
Transaction test succeeded.
Running transactionPreparing : 1/1 Installing : drpm-0.5.0-2.oe2203.x86_64 1/2 Installing : createrepo_c-0.17.6-1.oe2203.x86_64 2/2 Running scriptlet: createrepo_c-0.17.6-1.oe2203.x86_64 2/2 Verifying : createrepo_c-0.17.6-1.oe2203.x86_64 1/2 Verifying : drpm-0.5.0-2.oe2203.x86_64 2/2 Installed:createrepo_c-0.17.6-1.oe2203.x86_64 drpm-0.5.0-2.oe2203.x86_64 Complete!
[root@repo ~]#
[root@repo ~]# createrepo --update --workers=10 /home/repo
Directory walk started
Directory walk done - 16818 packages
type group added to list from path: /home/repo/repodata/93612b651befaec659f6700eab197afbbd9380df1bb302f73621ed1f4764940b-normal.xml
type group_gz added to list from path: /home/repo/repodata/c2a33c2e9423b23416c587e201ad7c690ef870f29998f4387f1cc9bea816d62e-normal.xml.gz
Loaded information about 16818 packages
Temporary output repo path: /home/repo/.repodata/
Preparing sqlite DBs
Pool started (with 10 workers)
Pool finished
[root@repo ~]#
👍 点赞,你的认可是我创作的动力!
⭐️ 收藏,你的青睐是我努力的方向!
✏️ 评论,你的意见是我进步的财富!

相关文章:

35 openEuler搭建repo(yum)服务器-创建、更新本地repo源
文章目录35 openEuler搭建repo(yum)服务器-创建、更新本地repo源35.1 获取ISO发布包35.2 挂载ISO创建repo源35.3 创建本地repo源35.4 更新repo源35 openEuler搭建repo(yum)服务器-创建、更新本地repo源 使用mount挂载,…...
【三.项目引入axios、申明全局变量、设置跨域】
根据前文《二.项目使用vue-router,引入ant-design-vue的UI框架,引入less》搭建好脚手架后使用 需求: 1.项目引入axios 2.申明全局变量 3.设置跨域 简介:axios本质上还是对原生XMLHttpRequest的封装,可用于浏览器和nodejs的HTTP客…...

启动u盘还原成普通u盘(Windows Diskpart)
使用windows系统的diskpart 命令解决系统盘恢复成普通U盘的问题:1. 按Windows R键打开运行窗口。在搜索框中输入“ Diskpart ”,然后按 Enter 键。2. 现在输入“ list disk ”并回车。3. 然后输入“ select disk X ”(将 X 替换为可启动U盘的…...
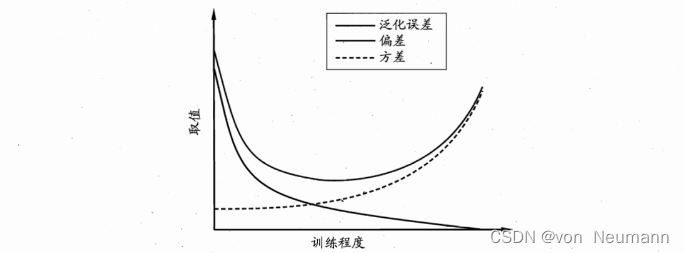
深入理解机器学习——偏差(Bias)与方差(Variance)
分类目录:《深入理解机器学习》总目录 偏差(Bias)与方差(Variance)是解释学习算法泛化性能的一种重要工具。偏差方差分解试图对学习算法的期望泛化错误率进行拆解,我们知道,算法在不同训练集上学…...

分布式新闻项目实战 - 13.项目部署_持续集成(Jenkins) ^_^ 完结啦 ~
欲买桂花同载酒,终不似,少年游。 系列文章目录 项目搭建App登录及网关App文章自媒体平台(博主后台)自媒体文章审核延迟任务kafka及文章上下架App端文章搜索后台系统管理Long类型精度丢失问题定时计算热点文章(xxl-Job…...

Linux c/c++技术方向分析
一、C与C介绍 1.1 说明 c语言是一门面向过程的、抽象化的通用程序设计语言,广泛应用于底层开发,如嵌入式。C语言能以简易的方式编译、处理低级存储器。是一种高效率程序设计语言。 c(c plus plus)是一种计算机高级程序设计语言&a…...
JavaScript 高级3 :函数进阶
JavaScript 高级3 :函数进阶 Date: January 19, 2023 Text: 函数的定义和调用、this、严格模式、高阶函数、闭包、递归 目标: 能够说出函数的多种定义和调用方式 能够说出和改变函数内部 this 的指向 能够说出严格模式的特点 能够把函数作为参数和返…...
【项目】Java树形结构集合分页,java对list集合进行分页
Java树形结构集合分页需求难点实现第一步:查出所有树形集合数据 (需进行缓存处理)selectTree 方法步骤:TreeUtil类:第二步:分页 GoodsCategoryController分页getGoodsCategoryTree方法步骤:第三…...
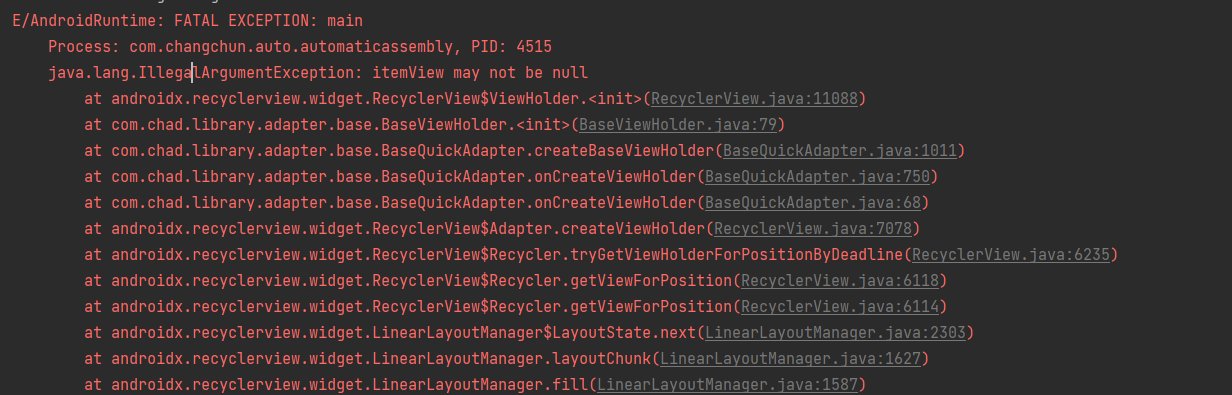
java.lang.IllegalArgumentException: itemView may not be null
报错截图:场景介绍:在使用recycleView 自动递增数据,且自动滚动到最新行; 当数据达到273条 时出现ANR;项目中 全部的列表适配器使用的三方库:BaseRecyclerViewAdapterHelper (很早之前的项目&am…...
[ 攻防演练演示篇 ] 利用 shiro 反序列化漏洞获取主机权限
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...

达人合作加持品牌布局,3.8女神玩转流量策略!
随着迅猛发展的“她经济”,使社区本就作为内容种草的平台,自带“营销基因”。在3.8女神节即将到来之际,如何充分利用平台女性资源优势,借助达人合作等手段,实现迅速引流,来为大家详细解读下。一、小红书节日…...
观点丨Fortinet谈ChatGPT火爆引发的网络安全行业剧变
FortiGuard报告安全趋势明确指出“网络攻击者已经开始尝试AI手段”,ChatGPT的火爆之际的猜测、探索和事实正在成为这一论断的佐证。攻守之道在AI元素的加持下也在悄然发生剧变。Fortinet认为在攻击者利用ChatGPT等AI手段进行攻击的无数可能性的本质,其实…...

工业企业用电损耗和降损措施研究
来自用电设备和供配电系统的电能损耗。而供配电系统的电能损耗,包括企业变配电设备、控制设备企业在不断降低生产成本,追求经济效益的情况下,进一步降低供配电系统中的电能损耗,使电气设摘要:电网电能损耗是一个涉及面很广的综合性问题,主要包括管理损耗和技术损耗两部分…...

高并发、高性能、高可用
文章目录一、高并发是什么?二、 高性能是什么三、 高可用什么是一、高并发是什么? 示例:高并发是现在互联网分布式框架设计必须要考虑的因素之一,它是可以保证系统能被同时并行处理很多请求,对于高并发来说࿰…...
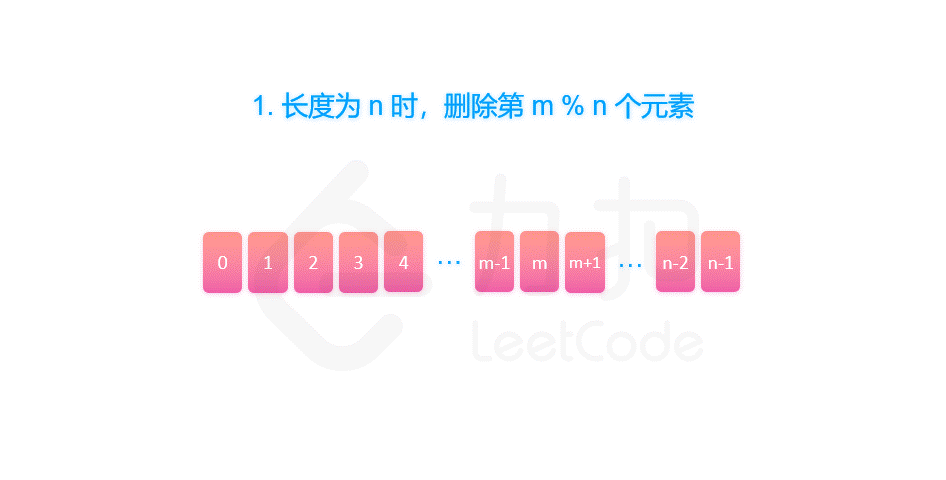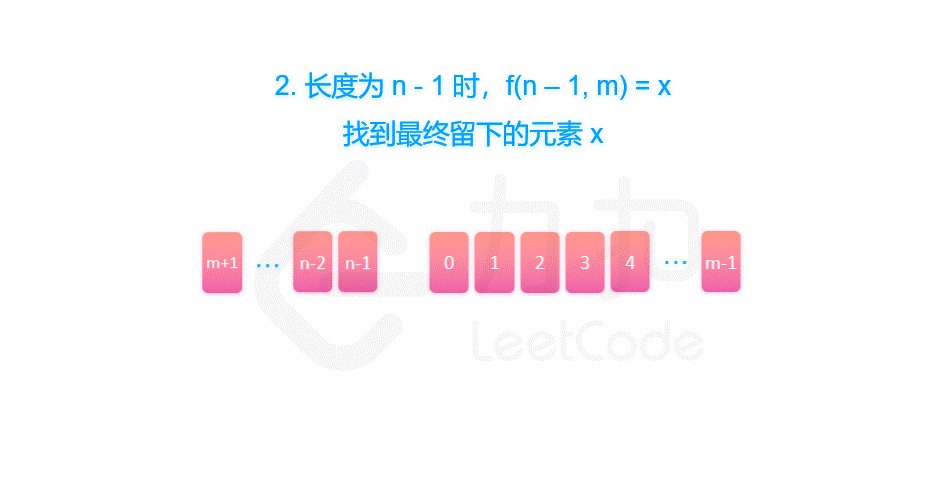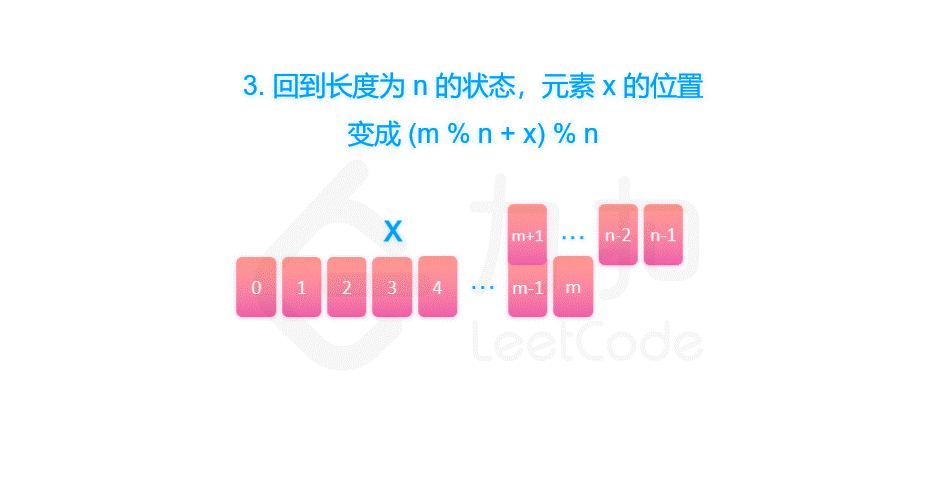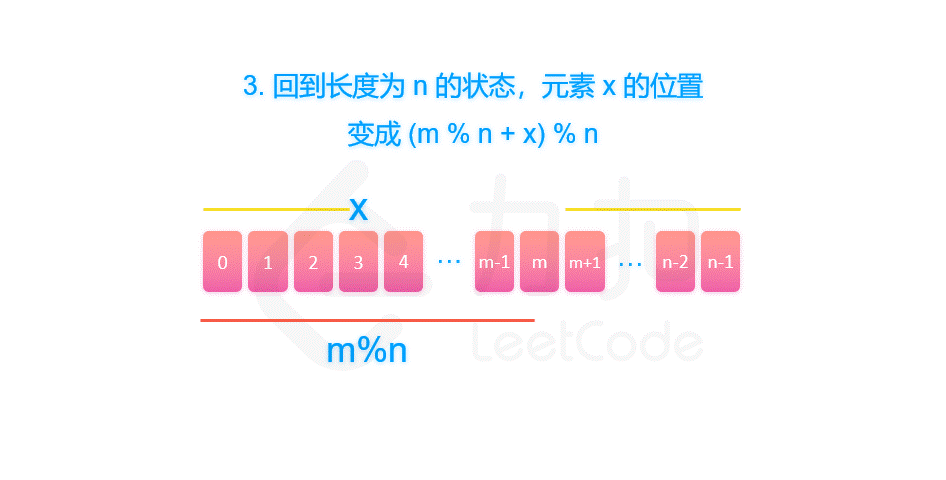
剑指 Offer 62. 圆圈中最后剩下的数字
摘要 剑指 Offer 62. 圆圈中最后剩下的数字 一、约瑟夫环解析 题目中的要求可以表述为:给定一个长度为 n 的序列,每次向后数 m 个元素并删除,那么最终留下的是第几个元素?这个问题很难快速给出答案。但是同时也要看到ÿ…...
概率论小课堂:高斯分布(正确认识大概率事件)
文章目录 引言I 预备知识1.1 正态分布1.2 置信度1.3 风险II 均值、标准差和发生概率三者的关系。2.1 “三∑原则”2.2 二班成绩比一班好的可能性2.3 减小标准差引言 泊松分布描述的是概率非常小的情况下的统计规律性。学习高斯分布来正确认识大概率事件,随机变量均值的差异和偶…...

剑指 Offer 43. 1~n 整数中 1 出现的次数
摘要 剑指 Offer 43. 1~n 整数中 1 出现的次数 一、数学思维解析 将1~ n的个位、十位、百位、...的1出现次数相加,即为1出现的总次数。 设数字n是个x位数,记n的第i位为ni,则可将n写为 nxnx−1⋯n2n1: 称" …...

如何成为程序员中的牛人/高手?
目录 一、牛人是怎么成为牛人的? 二、关于牛人的一点看法 三、让程序员与业务接壤,在开发团队中“升级” 四、使用低代码平台 目标效果 五、最后 祝伟大的程序员们梦想成真、码到成功! 一、牛人是怎么成为牛人的? 最近在某…...
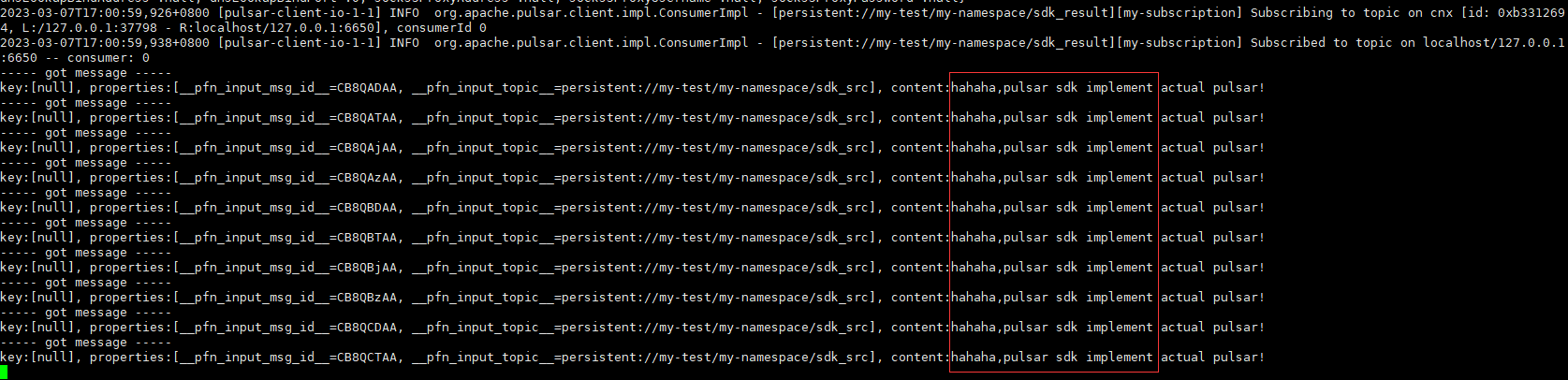
云原生时代顶流消息中间件Apache Pulsar部署实操之轻量级计算框架
文章目录Pulsar Functions(轻量级计算框架)基础定义工作流程函数运行时处理保证和订阅类型窗口函数定义窗口类型滚动窗口滑动窗口函数配置函数示例有状态函数示例窗口函数示例自定义函数开发定义原生语言接口示例Pulsar函数SDK示例Pulsar Functions(轻量级计算框架) 基础定义 …...
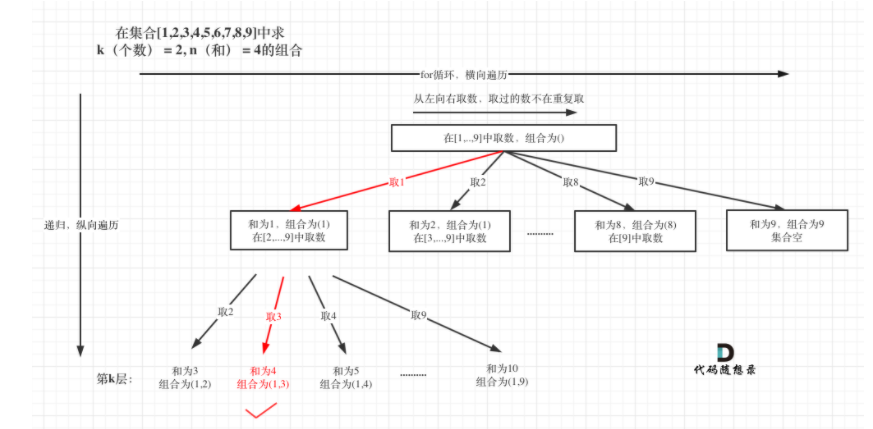
数据结构刷题(十九):77组合、216组合总和III
1.组合题目链接过程图:先从集合中取一个数,再依次从剩余数中取k-1个数。思路:回溯算法。使用回溯三部曲进行解题:递归函数的返回值以及参数:n,k,startIndex(记录每次循环集合从哪里开始遍历的位…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
