并查集(基础+带权以及可撤销并查集后期更新)
并查集
并查集是一种图形数据结构,用于存储图中结点的连通关系。
每个结点有一个父亲,可以理解为“一只伸出去的手”,会指向另一个点,初始时指向自己。一个点的根节点是该点的父亲的父亲的..的父亲,直到某个点的父亲是自己(根)。
当两个点的根相同时,我们就说他们时同一类,或者是连通的。
如下:7,5,1,3,6的根都是3,所以他们是连通的。
2,4是连通的,而2,6不连通,因为他们的根不同。
找根的方法
如果当前点不是根,就返回父亲的根。否则就是自己
用递归的方法实现
int find(int x)
{
if(pre[x]==x)retrun x;
return find(pre[x]);
}
并查集的合并
在并查集中所有的操作都在根上,假如我要使x和y两个点合并,我们只需要将find(x)指向find(y)或者find(y)指向find(x);
pre[find(x)]=find(y);
假如我们要合并4和6两点,我们只需要将2指向3或将3指向2.
路径压缩
找根函数的复杂度最坏情况下会达到O(n),如果查询次数较多的话效率将会非常低下。
我们可以在找根的过程中,将父亲指向根,从而实现路径压缩,这样可以使得找根的总体时间的复杂度为O(log n)。如下图,执行一次root(7)之后,沿途的点都会直接指向根3
int find(int x){
return pre[x]=(pre[x]==x?x:find(pre[x]));//当前的这个点是否是根,是根的话直接输出x不是根的话,去寻中这个根
}
例题
蓝桥幼儿园
题目描述
蓝桥幼儿园的学生是如此的天真无邪,以至于对他们来说,朋友的朋友就是自己的朋友。
小明是蓝桥幼儿园的老师,这天他决定为学生们举办一个交友活动,活动规则如下:
小明会用红绳连接两名学生,被连中的两个学生将成为朋友。
小明想让所有学生都互相成为朋友,但是蓝桥幼儿园的学生实在太多了,他无法用肉眼判断某两个学生是否为朋友。于是他起来了作为编程大师的你,请你帮忙写程序判断某两个学生是否为朋友(默认自己和自己也是朋友)。
输入描述
第 11 行包含两个正整数N,M,其中 N 表示蓝桥幼儿园的学生数量,学生的编号分别为1∼N。
之后的第2∼M+1 行每行输入三个整数op,x,y:
- 如果 op=1,表示小明用红绳连接了学生 x 和学生 y 。
- 如果 op=2,请你回答小明学生 x 和 学生 y 是否为朋友。
输出描述
对于每个op=2 的输入,如果 x 和 y 是朋友,则输出一行 YES,否则输出一行 NO。
输入输出样例
示例 1
输入
5 5
2 1 2
1 1 3
2 1 3
1 2 3
2 1 2
输出
NO
YES
YES代码
package chsi;
import java.util.*;
public class chapter1 {static int []pre;//定义一个数组表示每个结点的根是指向谁的public static void main(String[] args) {// TODO Auto-generated method stubScanner scan=new Scanner(System.in);int n=scan.nextInt();int m=scan.nextInt();pre=new int[n];//初始化prefor(int i=0;i<n;i++) pre[i]=i;//初始根都是指向它本身for(int i=0;i<m;i++) {int op=scan.nextInt();int x=scan.nextInt()-1;int y=scan.nextInt()-1;if(op==1) {union(x,y);}else {x=find(x);y=find(x);if(x==y) {System.out.println("YES");}else System.out.println("No");}}}public static int find(int x) {if(pre[x]!=x) {pre[x]=find(pre[x]);}//表示当前结点不是我们的根节点return pre[x];}//先写一个find查询,路径压缩的方式public static void union(int x,int y) {x=find(x);y=find(y);if(x!=y) {pre[x]=y;}return;}}
相关文章:
)
并查集(基础+带权以及可撤销并查集后期更新)
并查集 并查集是一种图形数据结构,用于存储图中结点的连通关系。 每个结点有一个父亲,可以理解为“一只伸出去的手”,会指向另一个点,初始时指向自己。一个点的根节点是该点的父亲的父亲的..的父亲,直到某个点的父亲…...
)
基于 Java 的数据结构和算法 (不定期更新)
JavaIsBestLang 数据结构 Collection 是 Java 中的接口,被多个泛型容器接口所实现。在这里,Collection 是指代存放对象类型的数据结构。 ArrayList 函数名功能size()返回 this 的长度add(Integer val)在 this 尾部插入一个元素add(int idx, Integer …...

考研回忆录【二本->211】
备考时长差不多快一年半,从22年的11月底开始陆陆续续地准备考研,因为开始的早所以整个备考过程显得压力不是很大,中途还去一些地方旅游,我不喜欢把自己绷得太紧。虽然考的不是很好,考完我甚至都没准备复试,…...
 Jiangxi Provincial Contest——ABCIJKL 做题记录)
【XCPC笔记】2023 (ICPC) Jiangxi Provincial Contest——ABCIJKL 做题记录
补题 赛后gym练习及补题,gym链接:2023 (ICPC) Jiangxi Provincial Contest – Official Contest 另外,D题我也打算找机会学习写下,C题的博弈论还需要好好理解,感觉都是比较有趣的数学问题 补题顺序如下 补题L [Zhang …...

猫头虎分享已解决Bug || **URLError (URL错误)** 全方位解析
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通鸿蒙》 …...
如何使用极狐GitLab 启用自动备份功能
本文作者:徐晓伟 GitLab 是一个全球知名的一体化 DevOps 平台,很多人都通过私有化部署 GitLab 来进行源代码托管。极狐GitLab 是 GitLab 在中国的发行版,专门为中国程序员服务。可以一键式部署极狐GitLab。 本文主要讲述了如何极狐GitLab 自…...

HTML/XML转义字符对照
特殊字符转义表 字符十进制转义字符""&&<<<>>>不断开空格(non-breaking space) 最常用的转义字符列表 显示说明实体名称十进制编号半方大的空白 全方大的空白 不断行的空白格 <小于<<>大于&g…...

设计模式:组合模式示例
组合模式的典型例子通常涉及到树形结构的处理,下面是几个形象且易于理解的例子: 文件系统 在文件系统中,目录可以包含文件或者其他目录,但是从用户的角度来看,目录和文件都可以被“打开”或者“获取大小”。这里的目…...
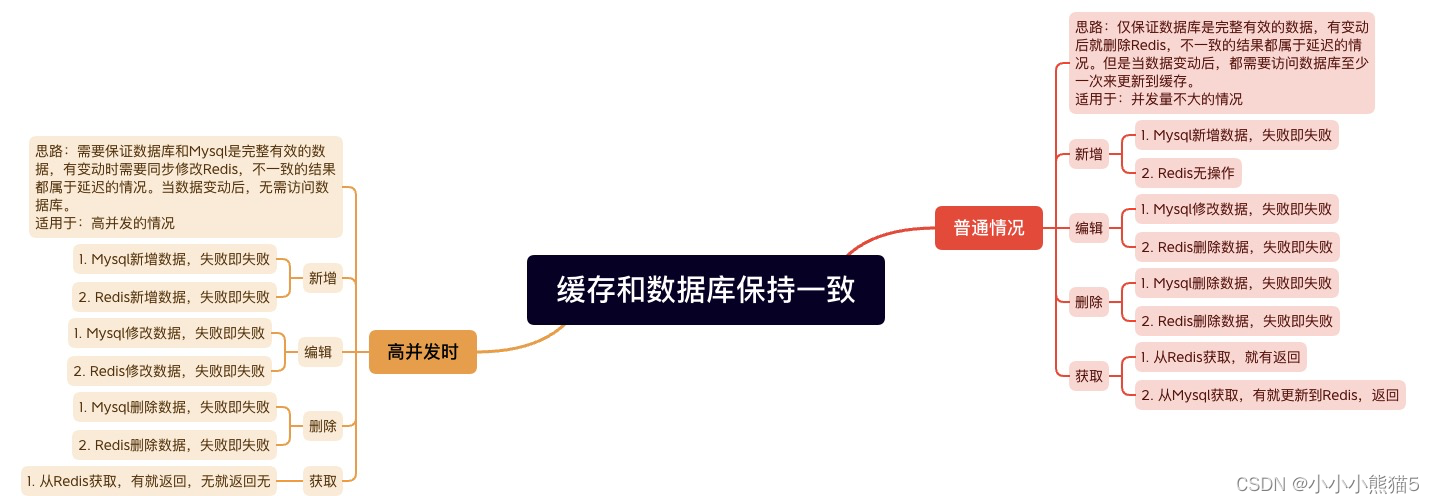
普通情况和高并发时,Redis缓存和数据库怎么保持一致?
普通情况和高并发时,Redis缓存和数据库怎么保持一致? 普通情况思路 高并发时思路 Q:缓存和数据库怎么保持一致? A:绝对不可能保持一致的,在实际业务开发中,有一些方案可以做取舍。 实际业务中&a…...

Django -- 自动化测试
概述 测试是一种例行的、不可缺失的工作,用于检查你的程序是否符合预期。 测试可以划分为不同的级别。一些测试可能专注于小细节(比如某一个模型的方法是否会返回预期的值?), 一些测试则专注于检查软件的整体运行是否…...

NodeJS 在Windows / Mac 上实现多版本控制
NodeJS 的多版本控制 本文介绍一下在 windows/MacOS 上 如何 切换和使用多个版本的 NodeJS。 Windows 本小节介绍一下在windows上管理不同版本的NodeJS。 nvm-windows 工具 nvm-windows 是在 windows 上管理 NodeJS 版本的一个工具。 它可以很方便的 下载、移除、查看、切…...

Web3 游戏周报(3.24-3.30)
【3.24-3.30】Web3 游戏行业动态: Web3 开发平台 Mirror World 在 Solana 上推出首个游戏 rollup 链 NFT 卡牌游戏 Parallel 完成 3,500 万美元融资,Solana Ventures 等参投 加密游戏开发公司 Gunzilla Games 完成 3,000 万美元融资 Telegram 游戏 No…...

算法思想1. 分治法2. 动态规划法3. 贪心算法4. 回溯法
目录 递归和动态的区别:空间和时间复杂度之争 递归空间复杂度低;动态时间复杂度第低...
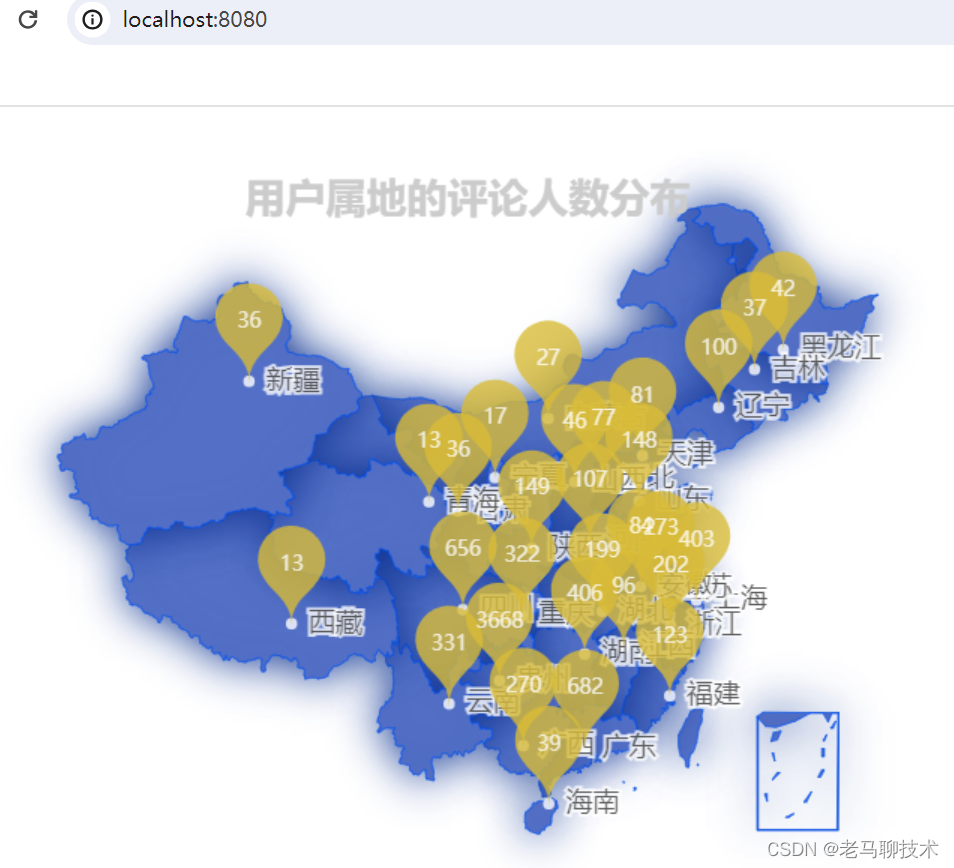
SpringBoot+ECharts+Html 地图案例详解
1. 技术点 SpringBoot、MyBatis、thymeleaf、MySQL、ECharts 等 此案例使用的地图是在ECharts社区中查找的:makeapie echarts社区图表可视化案例 2. 准备条件 在mysql中创建数据库echartsdb,数据库中创建表t_location_count表,表中设置两个…...

达梦数据库 优化
谁进行优化?优化什么? 优化不能仅从数据库方面考虑,比如,在存储达到数据库极限、应用涉及人员设计的代码稀巴烂的情况下,进行调优就是杯水车薪的效果。 涉及到优化人员: 数据库管理员应用程序架构师应用…...
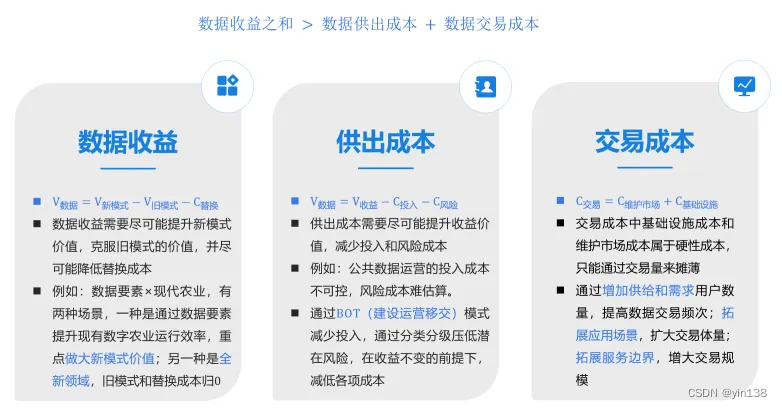
数据如何才能供得出、流得动、用得好、还安全
众所周知,数据要素已经列入基本生产要素,同时成立国家数据局进行工作统筹。目前数据要素如何发挥其价值,全国掀起了一浪一浪的热潮。 随着国外大语言模型的袭来,国内在大语言模型领域的应用也大放异彩,与此同时&#x…...
idea开发 java web 酒店推荐系统bootstrap框架开发协同过滤算法web结构java编程计算机网页
一、源码特点 java 酒店推荐推荐系统是一套完善的完整信息系统,结合java web开发和bootstrap UI框架完成本系统 采用协同过滤算法进行推荐 ,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式…...
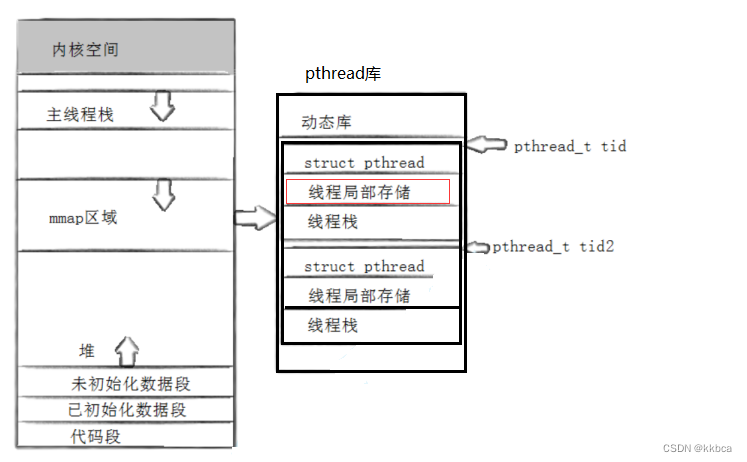
Linux——线程控制
目录 前言 一、线程创建 1.创建线程 2.线程传递结构体 3.创建多线程 4.收到信号的线程 二、线程终止 三、线程等待 四、线程分离 五、取消线程 六、线程库管理的原理 七、站在语言角度理解pthread库 八、线程的局部存储 前言 前面我们学习了线程概念和线程创建&…...

【Leetcode 347】,前k个高频元素,小根堆的调整
参考题解 题目:给定一个数组,输出 前k个高频元素。 思路: 遍历数组,建立小根堆(小根堆的元素是元组(num,freq),排序规则是每个元素的频率)。 下面使用数组‘heap’&…...

【图论】【分类讨论】LeetCode3017按距离统计房屋对数目
本文涉及的知识点 图论 分类讨论 本题同解 【差分数组】【图论】【分类讨论】【整除以2】3017按距离统计房屋对数目 LeetCode3017按距离统计房屋对数目 给你三个 正整数 n 、x 和 y 。 在城市中,存在编号从 1 到 n 的房屋,由 n 条街道相连。对所有 …...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
