堆排序解读
在算法世界中,排序算法一直是一个热门话题。推排序(Heap Sort)作为一种基于堆这种数据结构的有效排序方法,因其时间复杂度稳定且空间复杂度低而备受青睐。本文将深入探讨推排序的原理、实现方式,以及它在实际应用中的价值。
一、算法原理
推排序利用堆这种完全二叉树结构二叉堆的介绍)进行排序。堆通常分为最大堆和最小堆,其中最大堆的父节点值总是大于或等于其子节点值,而最小堆则相反。推排序通常使用最大堆来进行排序。
推排序的基本步骤包括:
- 建堆:将待排序的序列构造成一个大顶堆(最大堆)。此时,整个序列的最大值就是堆顶的根节点。
- 堆调整:将堆顶元素与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个序列重新构造成一个堆,这样会得到n个元素中的次大值。如此反复执行,便能得到一个有序序列。

二、代码实现
以下是使用Python语言实现推排序的示例代码:
def heapify(arr, n, i):""" 调整以i为根的子树,使其成为最大堆。 :param arr: 待排序的数组 :param n: 数组的长度 :param i: 当前根节点的索引 """largest = i # 初始化最大值为根 left = 2 * i + 1 # 左子节点索引 right = 2 * i + 2 # 右子节点索引 # 如果左子节点比根大 if left < n and arr[left] > arr[largest]:largest = left# 如果右子节点比当前最大值还大if right < n and arr[right] > arr[largest]:largest = right# 如果最大值不是根if largest != i:arr[i], arr[largest] = arr[largest], arr[i] # 交换 # 递归地调整受影响的子堆 heapify(arr, n, largest)def heap_sort(arr):""" 堆排序算法的主函数。 :param arr: 待排序的数组 """n = len(arr)# 构建最大堆 for i in range(n, -1, -1):heapify(arr, n, i)# 一个个从堆中取出元素 for i in range(n - 1, 0, -1):arr[i], arr[0] = arr[0], arr[i] # 将当前最大的元素移到数组末尾 heapify(arr, i, 0) # 重新调整堆 # 示例
arr = [12, 11, 13, 5, 6, 7]
heap_sort(arr)
print("排序后的数组:")
for i in range(len(arr)):print("%d" % arr[i]),
三、算法分析
推排序的时间复杂度为O(n log n),其中n是待排序元素的数量。这是因为建堆的时间复杂度为O(n),而每次调整堆(即从堆中取出最大元素并重新调整堆)的时间复杂度为O(log n)。由于需要执行n-1次这样的操作,因此总的时间复杂度为O(n log n)。
在空间复杂度方面,推排序是原地排序算法,只需要一个常量级别的额外空间来存储临时变量,因此空间复杂度为O(1)。
四、优缺点
推排序的优点在于其时间复杂度稳定且相对较低,同时空间复杂度也很低。此外,推排序是一种不稳定的排序算法,对于某些特定应用可能不是最佳选择。
然而,推排序在构建初始堆时,需要对整个数组进行遍历,这可能导致在处理小数据集时效率不如某些其他排序算法。此外,由于堆排序是一种比较排序,其性能可能受到数据特性的影响。
五、应用场景
推排序在实际应用中有着广泛的应用。由于其时间复杂度稳定且相对较低,推排序在处理大规模数据集时表现出色。它常被用于需要对大量数据进行排序的场景,如数据库查询优化、文件排序、大数据分析等。
相关文章:

堆排序解读
在算法世界中,排序算法一直是一个热门话题。推排序(Heap Sort)作为一种基于堆这种数据结构的有效排序方法,因其时间复杂度稳定且空间复杂度低而备受青睐。本文将深入探讨推排序的原理、实现方式,以及它在实际应用中的价…...

docker + miniconda + python 环境安装与迁移(详细版)
本文主要列出从安装dockerpython环境到迁移环境的整体步骤。windows与linux之间进行测试。 简化版可以参考:docker miniconda python 环境安装与迁移(简化版)-CSDN博客 目录 一、docker 安装和测试 二、docker中拉取minicondaÿ…...

蓝桥杯刷题第八天(dp专题)
这道题有点像小学奥数题,解题的关键主要是: 有2种走法固走到第i级阶梯,可以通过计算走到第i-1级和第i-2级的走法和,可以初始化走到第1级楼梯和走到第2级楼梯。分别为f[1]1;f[2]1(11)1(2)2.然后就可以循环遍历到后面的状态。 f[i…...

【WEEK6】 【DAY1】DQL查询数据-第一部分【中文版】
2024.4.1 Monday 目录 4.DQL查询数据(重点!)4.1.Data Query Language查询数据语言4.2.SELECT4.2.1.语法4.2.2.实践4.2.2.1.查询字段 SELECT 字段/* FROM 表查询全部的某某查询指定字段 4.2.2.2.给查询结果或者查询的这个表起别名(…...
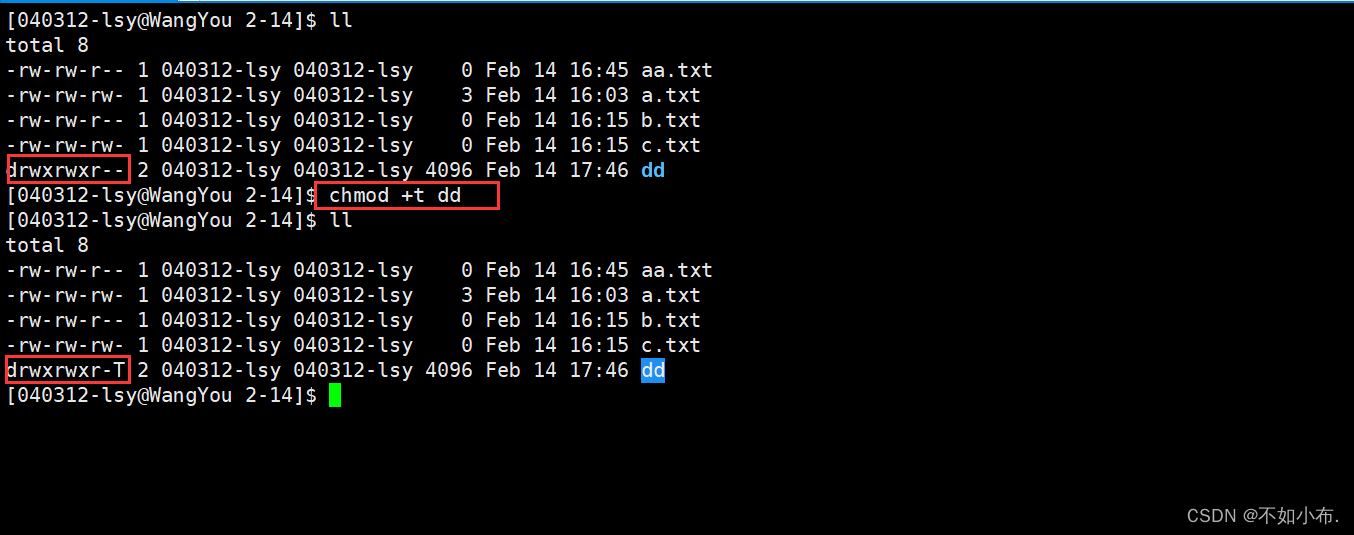
Linux:权限篇
文章目录 前言1.用户2.文件的权限管理2.1 修改文件的权限2.2 修改文件的拥有者2.3 修改文件的所属组 3.file指令4.umask指令4.目录的权限管理总结 前言 Linux权限在两个地方有所体现,一种是使用用户:分为root超级用户员与普通用户。另一个是体现在文件的…...
Lua热更新(xlua)
发现错误时检查是否:冒号调用 只需要导入asset文件夹下的Plugins和Xlua这两个文件即可,别的不用导入 生成代码 和清空代码 C#调用lua using Xlua; 需要引入命名空间 解析器里面执行lua语法 lua解析器 LuaEnv 单引号是为了避免引号冲突 第二个参数是报错时显示什么提示…...
)
并查集(基础+带权以及可撤销并查集后期更新)
并查集 并查集是一种图形数据结构,用于存储图中结点的连通关系。 每个结点有一个父亲,可以理解为“一只伸出去的手”,会指向另一个点,初始时指向自己。一个点的根节点是该点的父亲的父亲的..的父亲,直到某个点的父亲…...
)
基于 Java 的数据结构和算法 (不定期更新)
JavaIsBestLang 数据结构 Collection 是 Java 中的接口,被多个泛型容器接口所实现。在这里,Collection 是指代存放对象类型的数据结构。 ArrayList 函数名功能size()返回 this 的长度add(Integer val)在 this 尾部插入一个元素add(int idx, Integer …...

考研回忆录【二本->211】
备考时长差不多快一年半,从22年的11月底开始陆陆续续地准备考研,因为开始的早所以整个备考过程显得压力不是很大,中途还去一些地方旅游,我不喜欢把自己绷得太紧。虽然考的不是很好,考完我甚至都没准备复试,…...
 Jiangxi Provincial Contest——ABCIJKL 做题记录)
【XCPC笔记】2023 (ICPC) Jiangxi Provincial Contest——ABCIJKL 做题记录
补题 赛后gym练习及补题,gym链接:2023 (ICPC) Jiangxi Provincial Contest – Official Contest 另外,D题我也打算找机会学习写下,C题的博弈论还需要好好理解,感觉都是比较有趣的数学问题 补题顺序如下 补题L [Zhang …...

猫头虎分享已解决Bug || **URLError (URL错误)** 全方位解析
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通鸿蒙》 …...
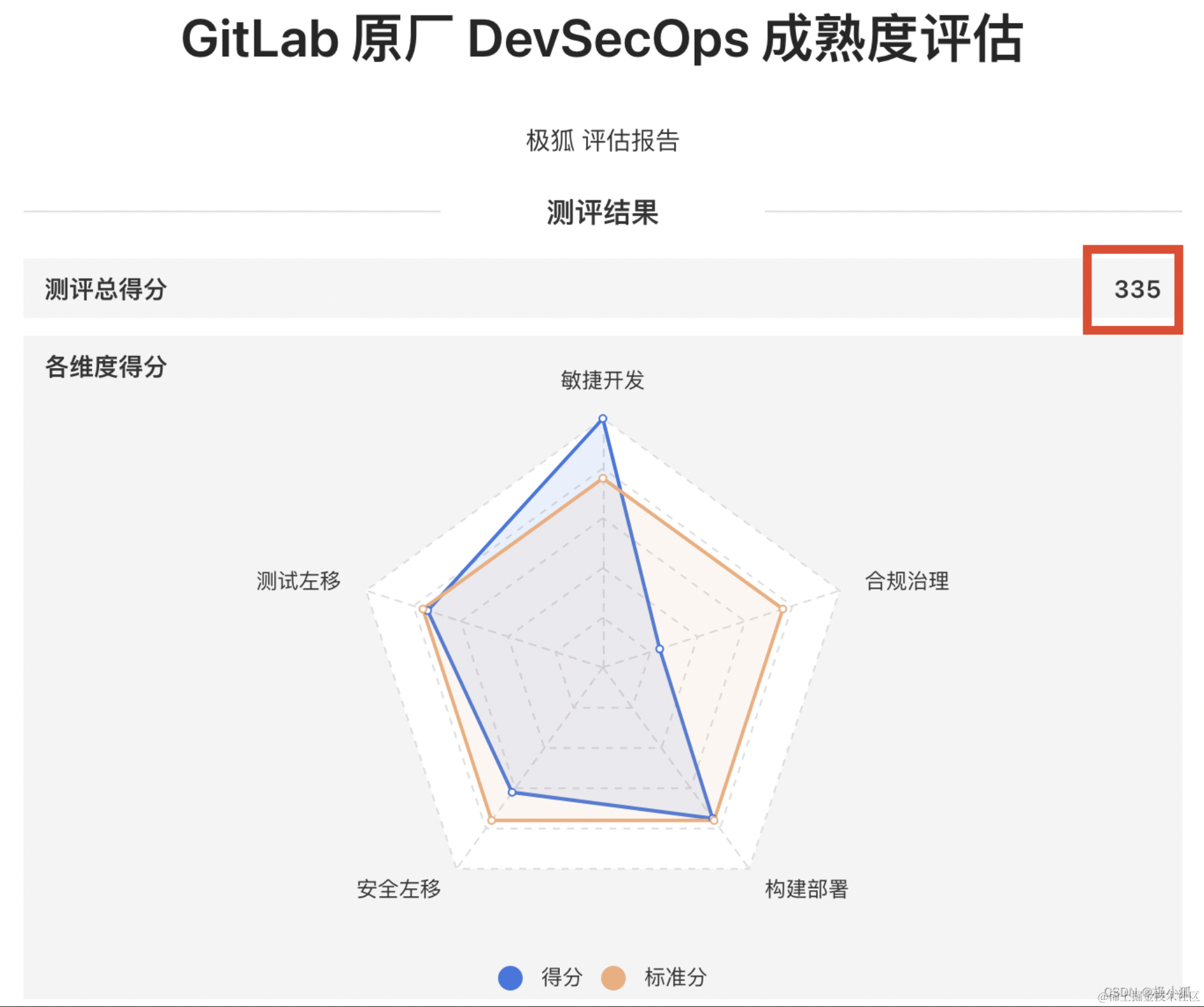
如何使用极狐GitLab 启用自动备份功能
本文作者:徐晓伟 GitLab 是一个全球知名的一体化 DevOps 平台,很多人都通过私有化部署 GitLab 来进行源代码托管。极狐GitLab 是 GitLab 在中国的发行版,专门为中国程序员服务。可以一键式部署极狐GitLab。 本文主要讲述了如何极狐GitLab 自…...

HTML/XML转义字符对照
特殊字符转义表 字符十进制转义字符""&&<<<>>>不断开空格(non-breaking space) 最常用的转义字符列表 显示说明实体名称十进制编号半方大的空白 全方大的空白 不断行的空白格 <小于<<>大于&g…...

设计模式:组合模式示例
组合模式的典型例子通常涉及到树形结构的处理,下面是几个形象且易于理解的例子: 文件系统 在文件系统中,目录可以包含文件或者其他目录,但是从用户的角度来看,目录和文件都可以被“打开”或者“获取大小”。这里的目…...
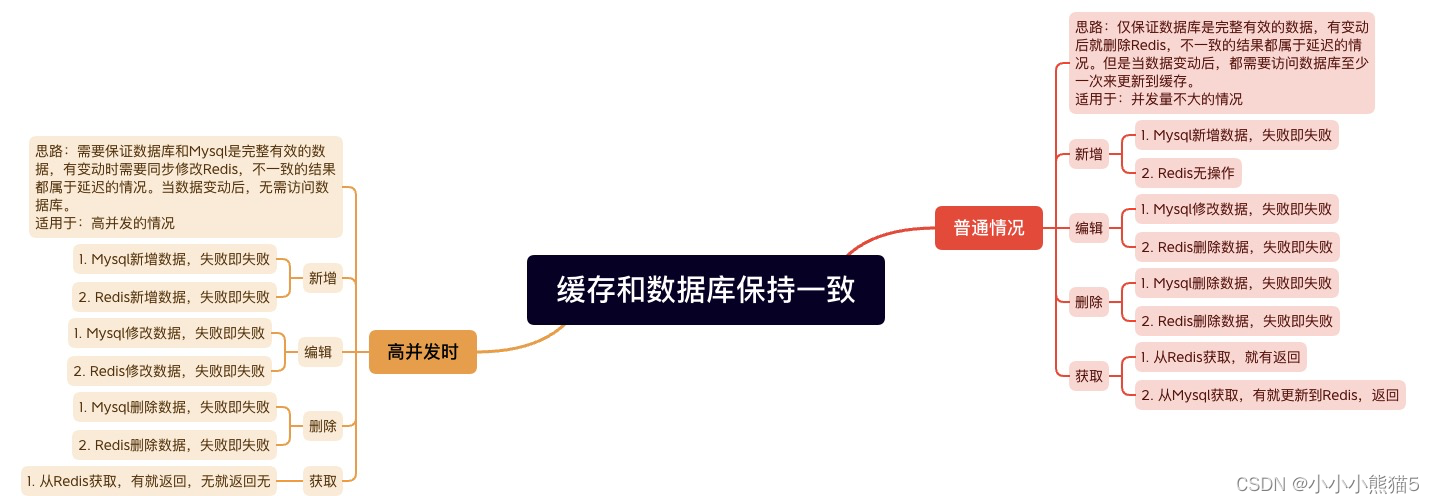
普通情况和高并发时,Redis缓存和数据库怎么保持一致?
普通情况和高并发时,Redis缓存和数据库怎么保持一致? 普通情况思路 高并发时思路 Q:缓存和数据库怎么保持一致? A:绝对不可能保持一致的,在实际业务开发中,有一些方案可以做取舍。 实际业务中&a…...

Django -- 自动化测试
概述 测试是一种例行的、不可缺失的工作,用于检查你的程序是否符合预期。 测试可以划分为不同的级别。一些测试可能专注于小细节(比如某一个模型的方法是否会返回预期的值?), 一些测试则专注于检查软件的整体运行是否…...

NodeJS 在Windows / Mac 上实现多版本控制
NodeJS 的多版本控制 本文介绍一下在 windows/MacOS 上 如何 切换和使用多个版本的 NodeJS。 Windows 本小节介绍一下在windows上管理不同版本的NodeJS。 nvm-windows 工具 nvm-windows 是在 windows 上管理 NodeJS 版本的一个工具。 它可以很方便的 下载、移除、查看、切…...

Web3 游戏周报(3.24-3.30)
【3.24-3.30】Web3 游戏行业动态: Web3 开发平台 Mirror World 在 Solana 上推出首个游戏 rollup 链 NFT 卡牌游戏 Parallel 完成 3,500 万美元融资,Solana Ventures 等参投 加密游戏开发公司 Gunzilla Games 完成 3,000 万美元融资 Telegram 游戏 No…...

算法思想1. 分治法2. 动态规划法3. 贪心算法4. 回溯法
目录 递归和动态的区别:空间和时间复杂度之争 递归空间复杂度低;动态时间复杂度第低...
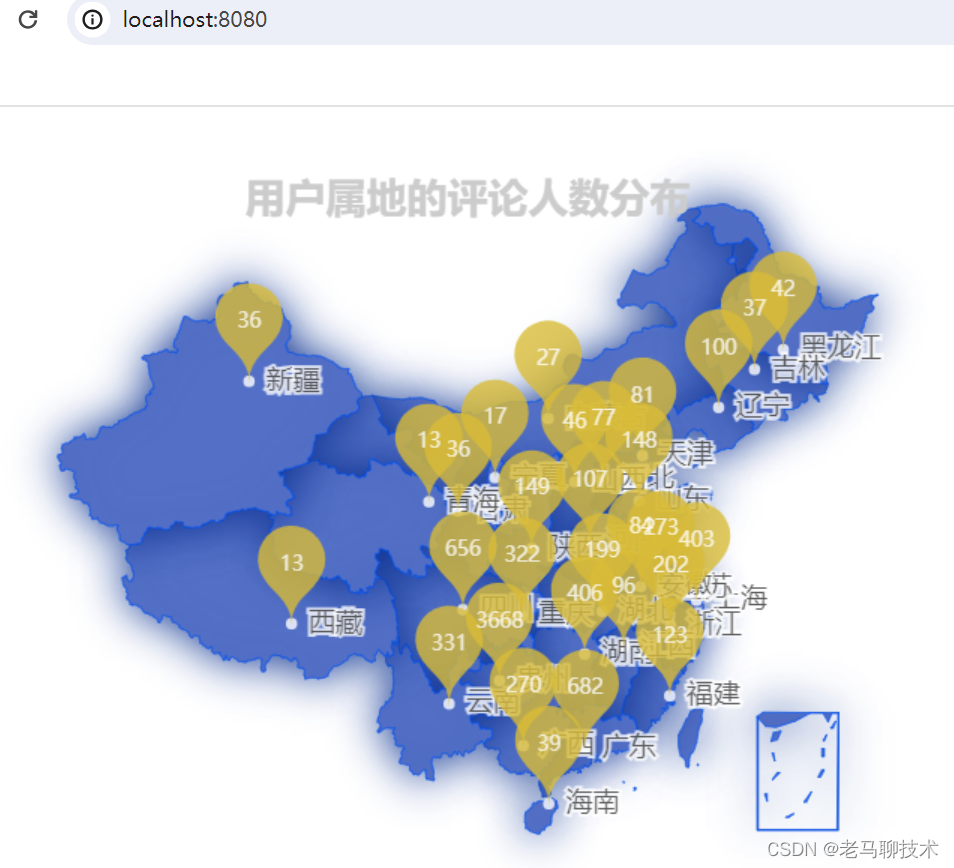
SpringBoot+ECharts+Html 地图案例详解
1. 技术点 SpringBoot、MyBatis、thymeleaf、MySQL、ECharts 等 此案例使用的地图是在ECharts社区中查找的:makeapie echarts社区图表可视化案例 2. 准备条件 在mysql中创建数据库echartsdb,数据库中创建表t_location_count表,表中设置两个…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
