excel统计分析——多项式回归
参考资料:生物统计学
多项式回归属于单变量曲线回归,但其形式和求解方法与多元线性回归相似。多项式回归的数学模型为:
令,
,
,
,则
由于X不可逆,两边同时乘以X'得,,两边在同时乘以X'X的逆矩阵,则:
进行回归方程的显著性检验时,可以直接用原始数据计算平方和:
检验偏回归系数的显著性时,,
为矩阵
对角线上的元素。和多元线性回归一样,当检验结果存在不显著的偏回归系数时,需逐步剔除不显著的项重新建立回归方程。
如果令,则多元线性回归方程和多项式回归方程的形式一致,多元线性回归方程也可以直接用原始数据求解。
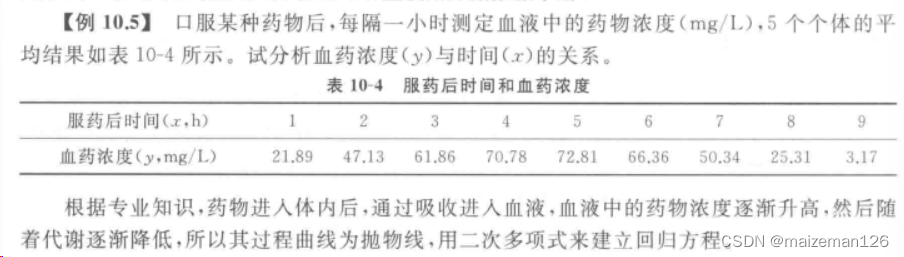
excel操作如下:
当然可以用数据分析工具直接求得偏回归系数和进行显著性检验,如下:
1、在数据分析工具对话框中,选择“回归”
2、选择对应的输入和输出区域。此处注意X值的输入区域不用选择列,只选择
和
列的数据。

3、导出结果
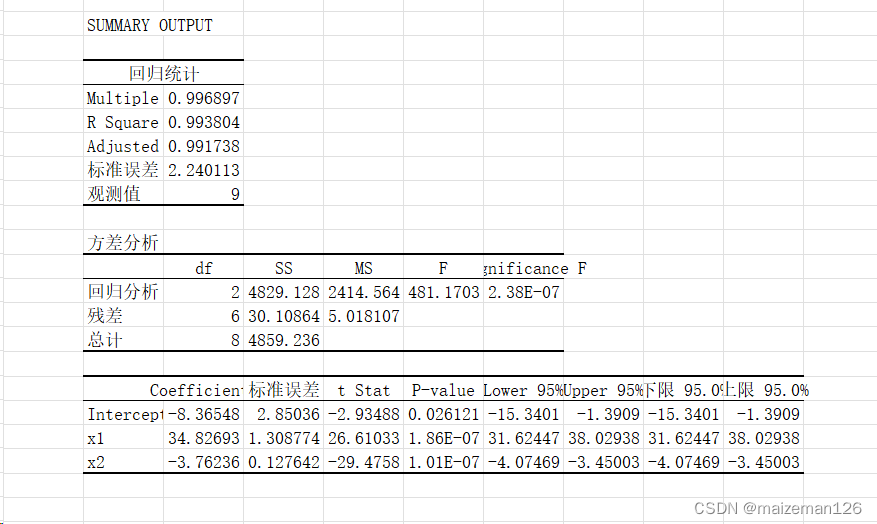
4、结果显示
回归方程显著,即存在回归关系;截距和两个偏回归系数均显著,表明y和x之间存在二次曲线回归关系。
相关文章:

excel统计分析——多项式回归
参考资料:生物统计学 多项式回归属于单变量曲线回归,但其形式和求解方法与多元线性回归相似。多项式回归的数学模型为: 令,,,,则 由于X不可逆,两边同时乘以X得,ÿ…...

SQLyog连接数据库8.0版本解析错误问题解决方案
问题描述: 解决方案: alter userrootlocalhostidentified with mysql_native_password by 密码; 再次连接就可以了。...

【数据库】SQL简介
SQL(Structured Query Language,结构化查询语言)是一种用于管理关系型数据库管理系统(RDBMS)的标准化语言。它用于访问和操作数据库中的数据,执行各种任务,如插入、更新、删除和检索数据&#x…...
AWS入门实践-利用S3构建一个静态网站
使用Amazon S3托管静态网站是一个流行的选择,因为它简单、成本效益高,并且易于维护。静态网站由不含服务器端脚本的文件组成,如HTML、CSS和JavaScript文件。下面是使用S3托管静态网站的操作步骤: 如果大家没有AWS免费账号&#x…...

使用Linux strace追踪系统调用: 一个详细指南
使用Linux strace追踪系统调用: 一个详细指南 Linux strace是一个强大的命令行工具,用于监视和调试进程中发生的系统调用和信号。它对于系统管理员和开发人员来说是理解程序行为和解决问题的重要工具。 什么是strace? strace是一种跟踪运行中的进程执…...

python 笔记
文章目录 pdbpdb开始调试pythonpdb设置断点单步执行进入到函数的内部执行到下一个断点或程序结束调用栈查看命令查看当前函数调用堆栈向上一层函数查看调用堆栈查看源代码 importimport 用法 numpy导入numpy模块numpy常用函数np.argmaxnp.sum range生成连续序列生成不连续序列 …...
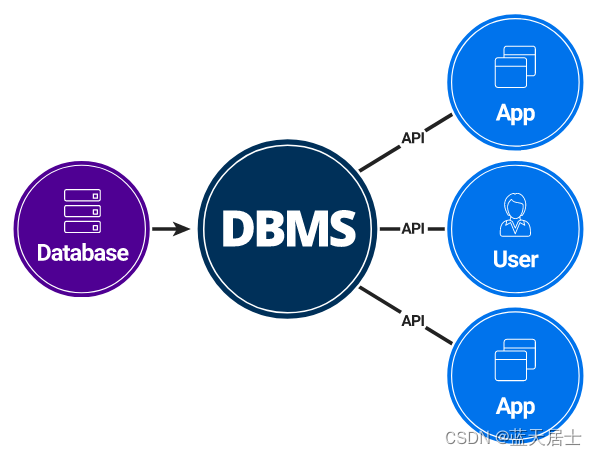
软考 系统架构设计师系列知识点之数据库基本概念(4)
接前一篇文章:软考 系统架构设计师系列知识点之数据库基本概念(3) 所属章节: 第6章. 数据库设计基础知识 第1节 数据库基本概念 6.1.3 数据库管理系统 DBMS(DataBase Management System,数据库管理系统&am…...
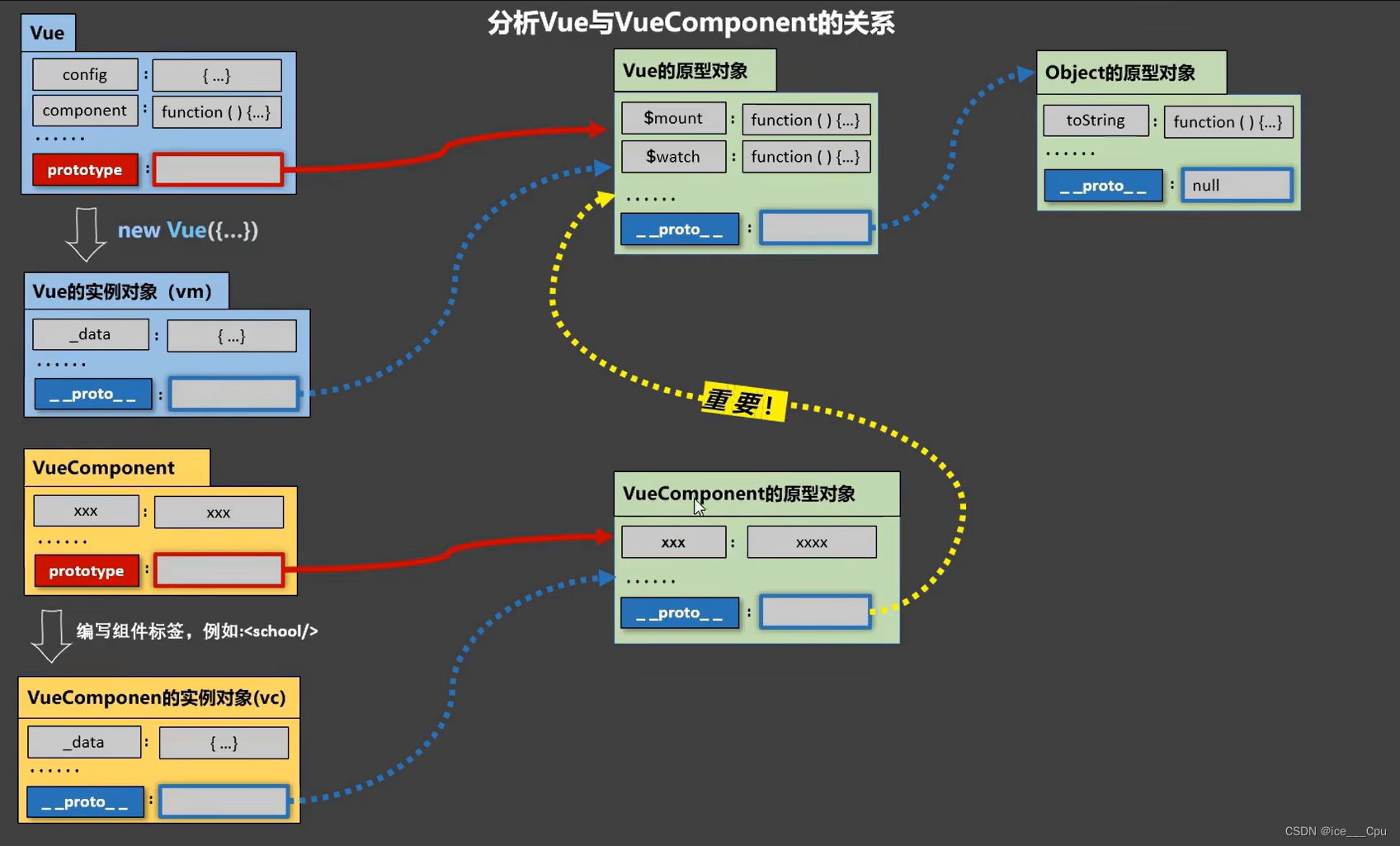
Vue - 3( 15000 字 Vue 入门级教程)
一:初识 Vue 1.1 收集表单数据 收集表单数据在Vue.js中是一个常见且重要的任务,它使得前端交互变得更加灵活和直观。 Vue中,我们通常使用v-model指令来实现表单元素与数据之间的双向绑定,从而实现数据的收集和更新。下面总结了…...
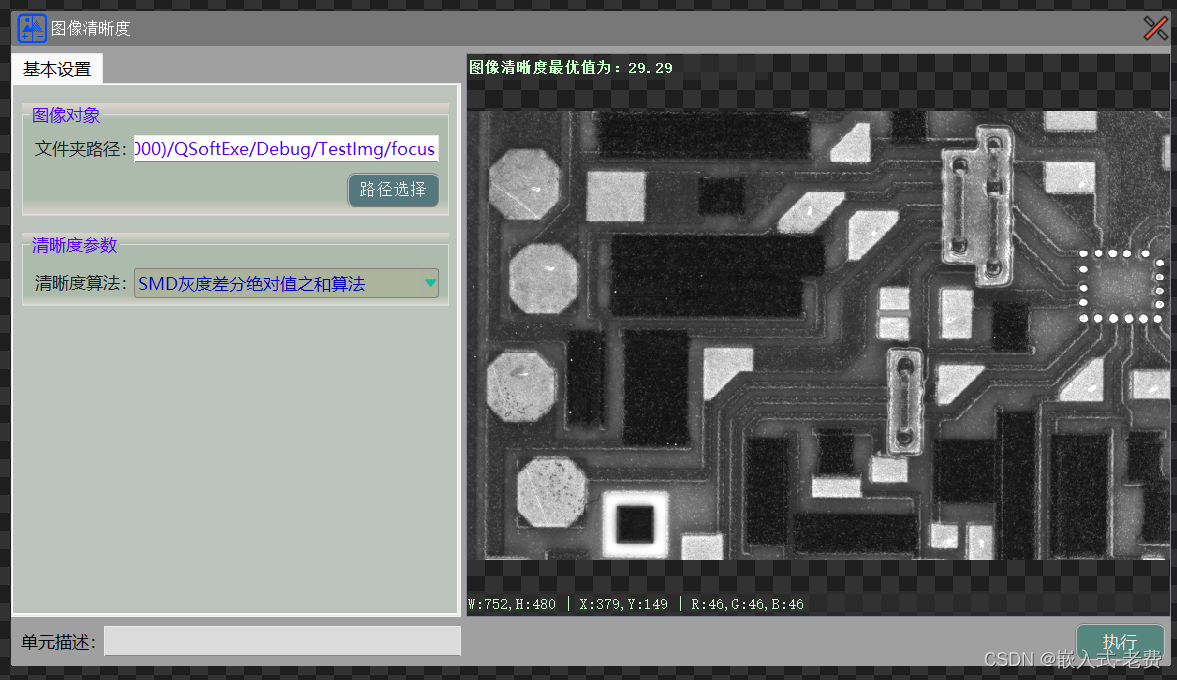
上位机图像处理和嵌入式模块部署(qmacvisual图像清晰度)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 做过isp的同学都知道,图像处理里面有一个3A,即自动曝光、自动白平衡和自动对焦。其中自动对焦这个,就需要用输入…...
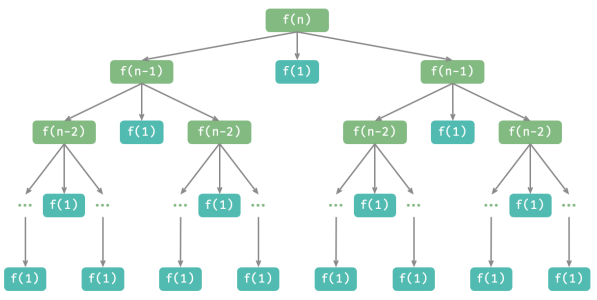
数据结构和算法:分治
分治算法 分治(divide and conquer),全称分而治之,是一种非常重要且常见的算法策略。分治通常基于递归实现,包括“分”和“治”两个步骤。 1.分(划分阶段):递归地将原问题分解为两个…...

增强Java技能:使用OkHttp下载www.dianping.com信息
在这篇技术文章中,我们将探讨如何使用Java和OkHttp库来下载并解析www.dianping.com上的商家信息。我们的目标是获取商家名称、价格、评分和评论,并将这些数据存储到CSV文件中。此外,我们将使用爬虫代理来绕过任何潜在的IP限制,并实…...

用友 NC saveXmlToFIleServlet 任意文件上传漏洞复现
0x01 产品简介 用友NC是一款企业级ERP软件。作为一种信息化管理工具,用友NC提供了一系列业务管理模块,包括财务会计、采购管理、销售管理、物料管理、生产计划和人力资源管理等,帮助企业实现数字化转型和高效管理。 0x02 漏洞概述 用友 NC saveXmlToFIleServlet接口处存在…...

JS第九天
今天是第九天,学习了JS中的设置日期和倒计时,计时器以及验证码倒计时,那么话不多说我们开始今天的学习吧 一、日期设置 1.1日期创建 调用 new Date() 来创建一个新的 Date 对象。在调用时可以带有一些参数,创建一个 Date 对象&…...

CSS设置字体样式
目录 前言: 1.font-family: 2.font-style: 3.font-weight: 4.font-size: 5.font-variant: 6.font: 前言: 在网页中字体是重要的组成部分,使用好字体可以让网页更…...
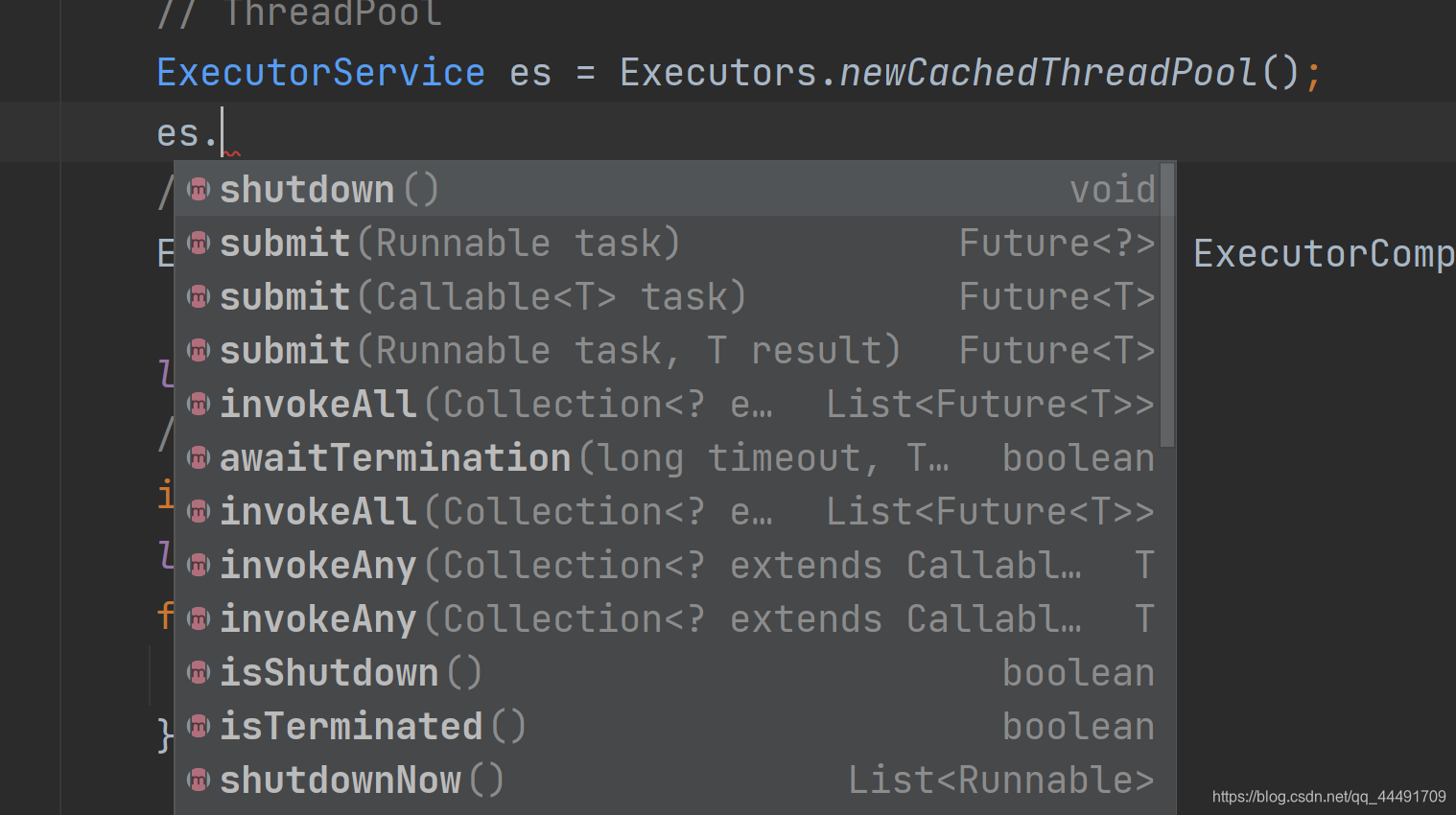
[Java线程池]ExecutorService|CompletionService的区别与选择
这段时间对业务系统做了个性能测试,其中使用了较多线程池的技术,故此做一个技术总结。 这次总结的内容比较多,主要是四个: ExecutorServiceCompletionServiceRunnableCallable 前两个是线程池相关接口,后两个是多线…...
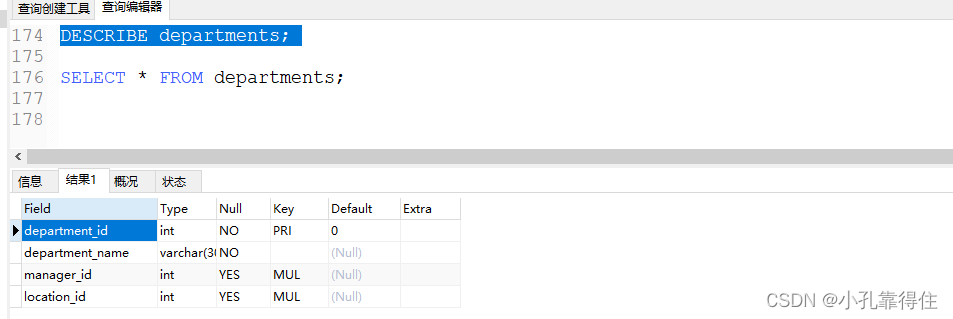
MySQL-SQL编写练习:基本的SELECT语句
基本的SELECT语句 1. SQL的分类 DDL:数据定义语言。CREATE \ ALTER \ DROP \ RENAME \ TRUNCATEDML:数据操作语言。INSERT \ DELETE \ UPDATE \ SELECT (重中之重)DCL:数据控制语言。COMMIT \ ROLLBACK \ SAVEPOINT \ GRANT \ REVOKE 学习技巧…...
)
C++经典面试题目(十九)
1、什么是析构函数?它有什么作用? 析构函数是类的特殊成员函数,用于在对象被销毁时执行清理工作。它的名称与类名相同,前面加上波浪号(~)。析构函数的作用在于确保在对象被销毁时释放占用的资源࿰…...

acwing算法提高之图论--SPFA找负环
目录 1 介绍2 训练 1 介绍 本专题用来记录使用spfa算法来求负环的题目。 2 训练 题目1:904虫洞 C代码如下, #include <cstring> #include <iostream> #include <algorithm> #include <queue>using namespace std;typedef p…...
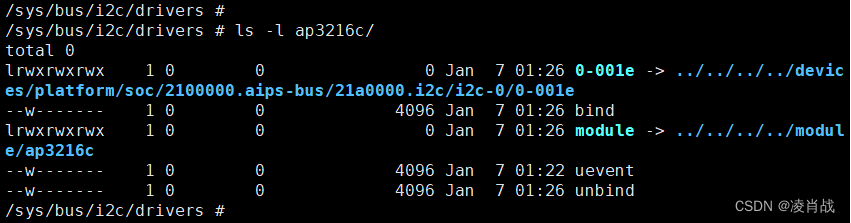
I2C驱动实验:测试I2C驱动是否与设备匹配
一. 简介 前面一篇文章在设备树中创建 ap3216c设备节点信息。 第二篇文章编写了简单的 I2C设备驱动框架,包括 构造 i2c_driver结构体,i2c_driver的注册与注销等。文章如下: I2C驱动实验:向设备树添加 I2C设备的设备节点信息-C…...

5560.树的直径
蛮不错的一道题目,你要利用树的性质分析出,你只需要维护上一次的树的直径的两个端点就好了 #include<iostream>using namespace std; using ll long long; using pii pair<int,int>; const int N 6e510; const int inf 0x3f3f3f3f; cons…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
